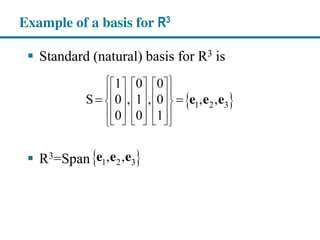
1. A basis for a vector space is a set of linearly independent vectors that span the entire space. The standard basis for Rn is the set of n unit vectors e1, e2, ..., en. 2. The dimension of a vector space is the number of vectors in any of its bases. A vector space with dimension n has bases that contain exactly n vectors. 3. The null space of a matrix A consists of all vectors x such that Ax = 0. The dimension of the null space is called the nullity of A, and the null space always has a basis.

1. 4. Vector Spaces
BASES
and
DIMENSION
for
VECTOR SPACES

2. Basis
Defn - A set of vectors S = { v1, v2, , vk } in
a vector space V is called a basis for V
if and only if
S is
a) linearly independent
and
a) S spans V.

3. Standard (natural) basis for R2 is
R2=Span
Also R2=Span
Therefore, is another basis for R2
Example of a basis for R2
1 2
1 0
S , ,
0 1
e e
𝐞 , 𝐞
2 1
,
1 3
2 1
,
1 3

4. Standard (natural) basis for R3 is
R3=Span
1 2 3
1 0 0
S 0 , 1 , 0 , ,
0 0 1
e e e
Example of a basis for R3
1 2 3, ,e e e

5. The following three-dimensional vectors are linearly
independent.
Any vector in R3 can be expressed as a linear
combination of v1, v2 and v3.
v1, v2 and v3 form a basis of R3.
Span {v1, v2 , v3} = R3.
1 2 3
1 1 1
2 , 0 , 1
1 2 0
v v v
Example of a basis for R3

6. The standard (natural) basis for Rn is
denoted by e1, e2, , en where
0
0
th row1
0
0
i ie
Example of a basis for Rn

7. Theorem - If S = { v1, v2, , vn } is a basis
for a vector space V, then every vector in V
can be written in one and only one way as a
linear combination of the vectors in S
Theorem - If S = { v1, v2, , vn } is a set of
vectors spanning a vector space V, then S
contains a basis T for V
Basis

8. Theorem - If S = { v1, v2, , vn } is a basis for
a vector space V and T = { w1, w2, , wr } is
a linearly independent set of vectors in V, then
r ≤ n.
Corollary - If S = { v1, v2, , vn } and
T = { w1, w2, , wm } are bases for a
vector space V, then n = m,
i.e.
every basis for V contains the same number of
vectors.
Basis

9. Defn - The dimension of a nonzero vector
space V is the number of vectors in a basis
for V.
Notation is dim V.
The dimension of the trivial vector space
{ 0 } is defined as 0.
Dimension of a Vector Space

10. Corollary - If a vector space V has dimension
n, then a largest linearly independent subset of
vectors in V contains n vectors and is a basis
for V
Corollary - If a vector space V has dimension
n, the smallest set of vectors that spans V
contains n vectors and is a basis for V.
Basis and Dimension

11. Corollary - If vector space V has dimension n,
then any subset of m > n vectors must be
linearly dependent.
Corollary - If vector space V has dimension n,
then any subset of m < n vectors cannot span
V.
Theorem - If S is a linearly independent set of
vectors in a finite dimensional vector space V,
then there is a basis T for V, which contains S.
Basis and Dimension

12. Theorem - Let V be an n-dimensional vector
space
a) If S = { v1, v2, , vn } is a linearly
independent set of vectors in V, then S is a
basis for V.
b) If S = { v1, v2, , vn } spans V, then S is a
basis for V.
Basis and Dimension

13. Consider the homogeneous system Ax = 0 where
A reduces to
Basis for Solution Sets : Homogeneous
1 2 2 2 3 0
4 6 4 6 6 4
1 3 4 2 4 0
2 4 4 3 4 2
A
1 0 2 0 3 4
0 1 2 0 1 0
0 0 0 1 2 2
0 0 0 0 0 0

14. Corresponding system of equations is
51 3 6
52 3
54 6
2 3 4 0
2 0
2 2 0
x x x x
x x x
x x x
1
2
3
4
5
6
2 3 4 2 3 4
2 2 1 0
1 0 0
2 2 0 2 2
0 1 0
0 0 1
x r s t
x r s
x r
r s t
x s t
x s
x t
Let x6 = t, x5 = s, x3 = r
Then x4 = –2s + 2t,
x2 = –2r – s,
x1 = 2r + 3s – 4t
Basis for Solution Sets : Homogeneous

15. The null space of A is spanned by the independent
set of 3 vectors (below) and thus has dimension 3.
Dimension of null space is called the nullity of A.
2 3 4
2 1 0
1 0 0
, ,
0 2 2
0 1 0
0 0 1
Basis for Solution Sets : Homogeneous

16. Consider the linear system
The solution consists of all vectors of the form
for arbitrary r and s
Basis for Solution Sets : Nonhomogeneous
1
2
3
1 2 1 3
2 4 2 6
3 6 3 9
x
x
x
1
2
3
1 2 1 2 1
1 1 1 0
2 2 0 1
x r s
x r r s
x s

17. The set of linear combinations, ,
forms a plane
passing through the origin of R3.
This plan is a linear space.
Basis for Solution Sets
2 1
1 0
0 1
r s

18. The solution vectors, ,
form a plane parallel to the plane above,
displaced from the origin by the vector
This plan is not a linear space.
Basis for Solution Sets
1 2 1
1 1 0
2 0 1
r s
1
1
2

19. Section 4.4
p.259, p.260
1 to 10; 12 to 20;
Problems