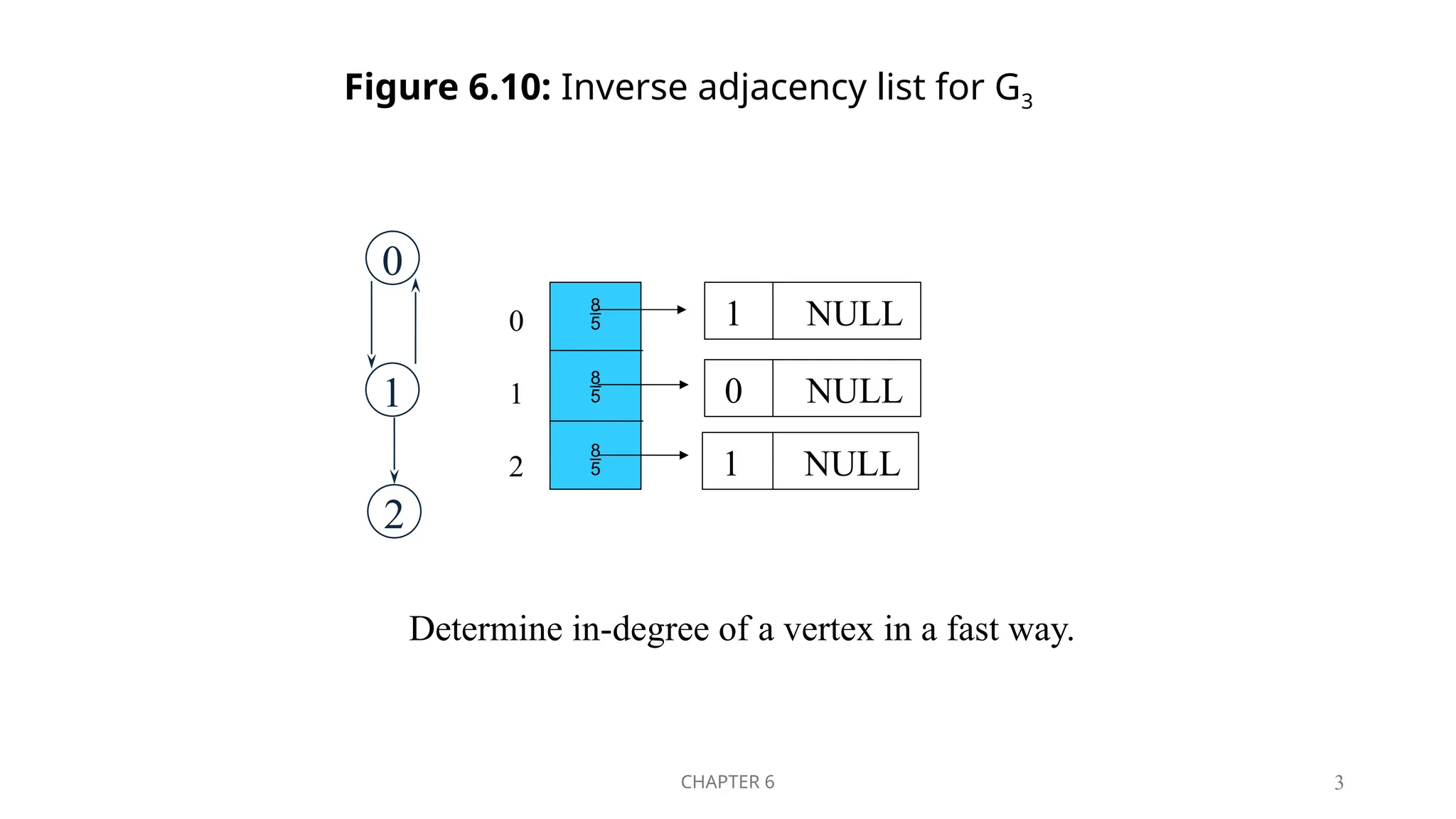
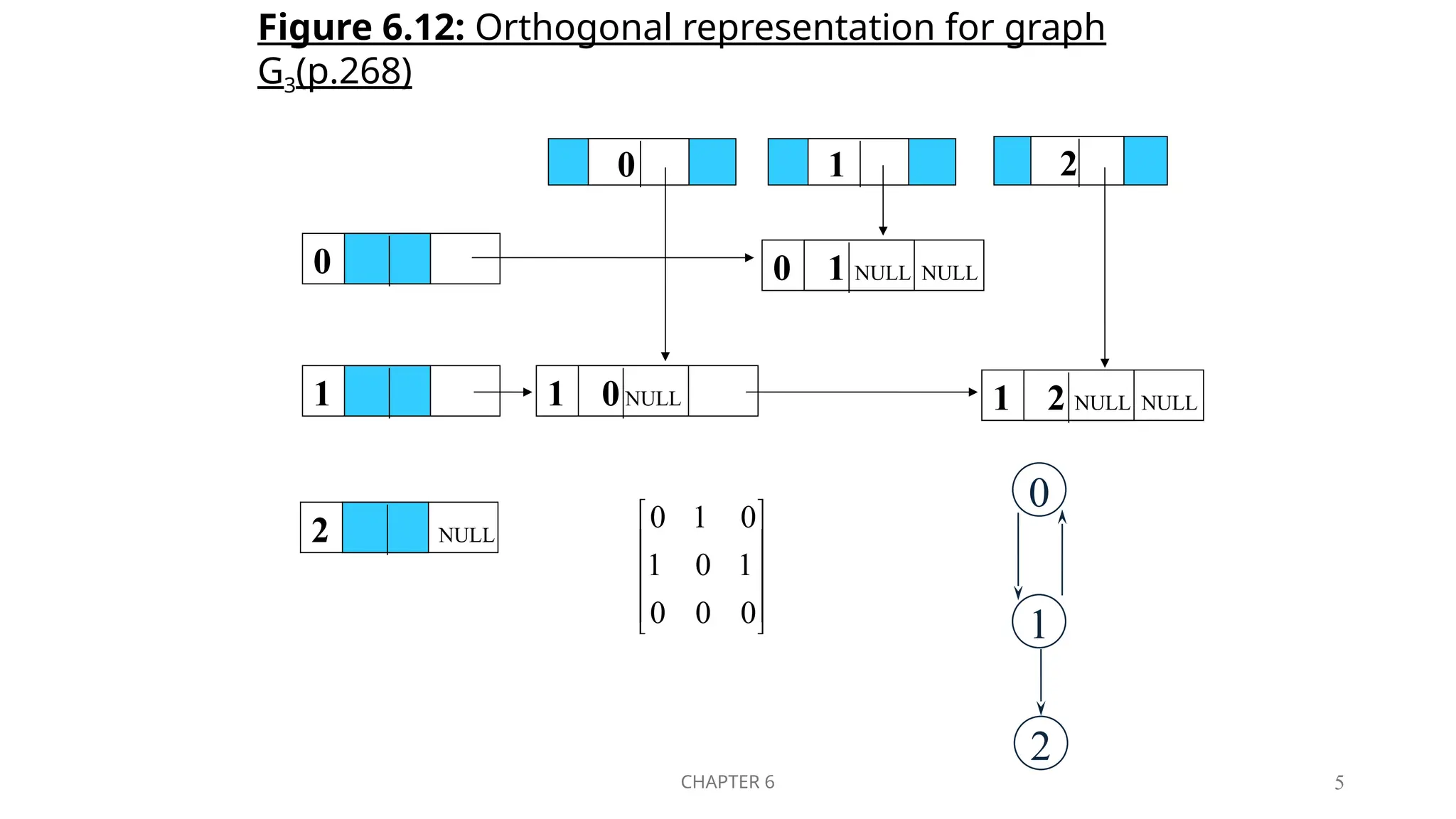
The document appears to discuss concepts related to graph theory, specifically chapters 6 and 7, including adjacency lists and vertex structures. It references figures that illustrate various representations of graph data and methods for determining in-degrees efficiently. Additionally, it includes structural details for both head and tail nodes in an alternate node structure.

1. Chapter 7

2. CHAPTER 6 2
[0] 9 [8] 23 [16] 2
[1] 11 [9] 1 [17] 5
[2] 13 [10] 2 [18] 4
[3] 15 [11] 0 [19] 6
[4] 17 [12] 3 [20] 5
[5] 18 [13] 0 [21] 7
[6] 20 [14] 3 [22] 6
[7] 22 [15] 1
1
0
2
3
4
5
6
7
0
1
2
3
4
5
6
7
node[0] … node[n-1]: starting point for vertices
node[n]: n+2e+1
node[n+1] … node[n+2e]: head node of edge
Compact Representation

3. CHAPTER 6 3



0
1
2
1 NULL
0 NULL
1 NULL
0
1
2
Determine in-degree of a vertex in a fast way.
Figure 6.10: Inverse adjacency list for G3

4. CHAPTER 6 4
tail head column link for head row link for tail
Figure 6.11: Alternate node structure for adjacency lists
(p.267)

5. CHAPTER 6 5
0 1 2
2 NULL
1
0
1 0NULL
0 1 NULL NULL
1 2 NULL NULL
0
1
2
0
1
0
1
0
0
0
1
0










Figure 6.12: Orthogonal representation for graph
G3(p.268)