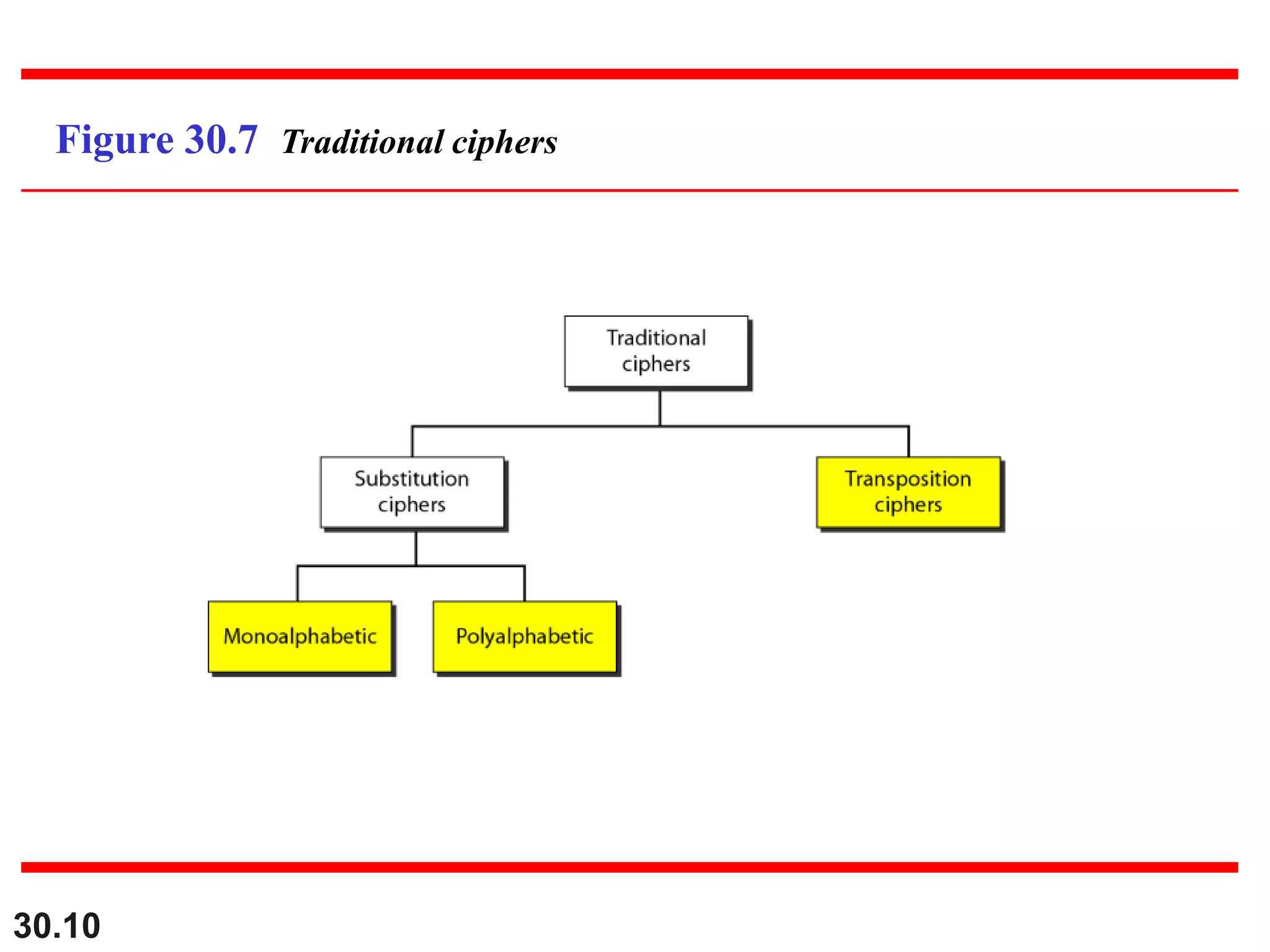
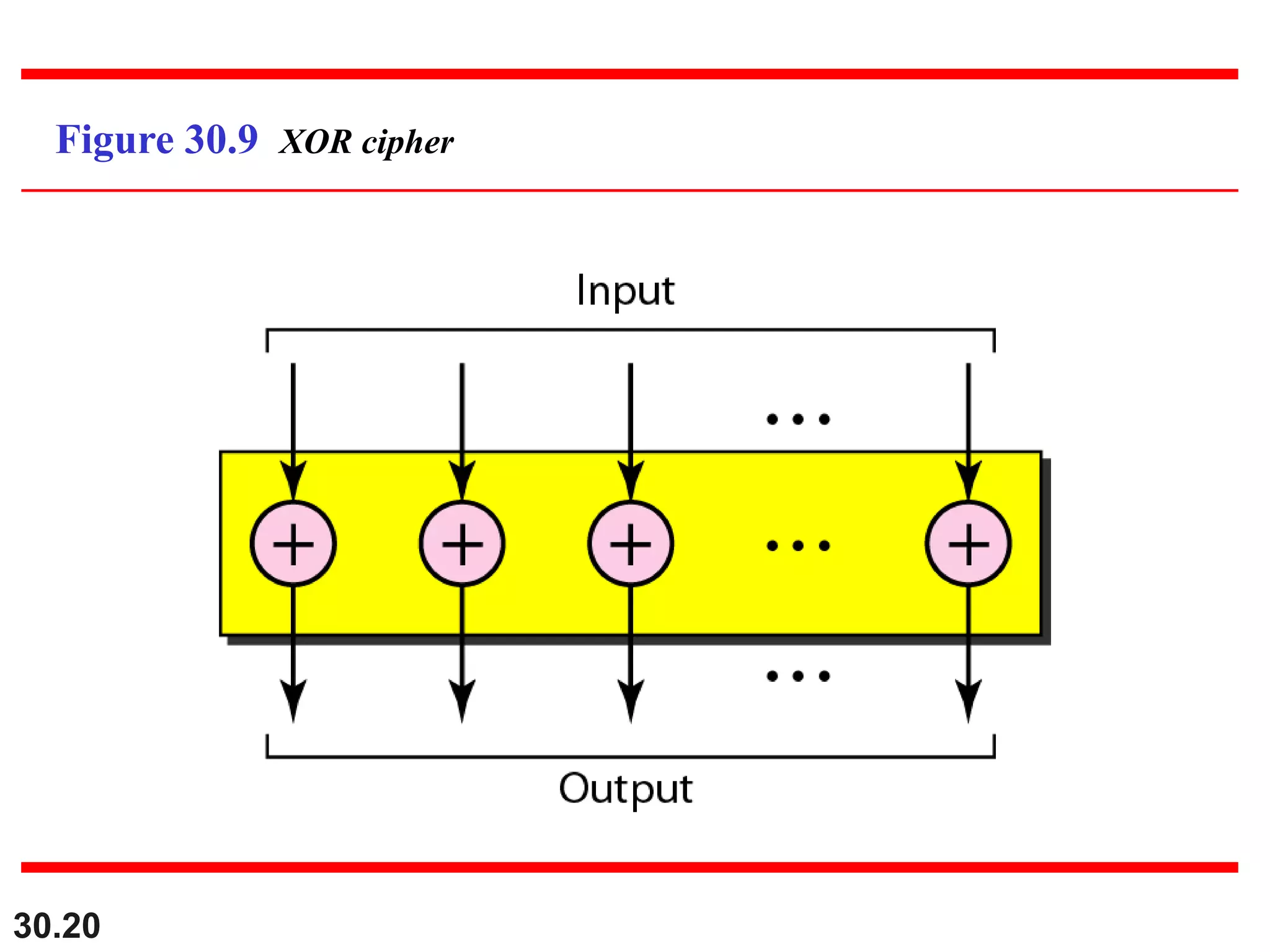
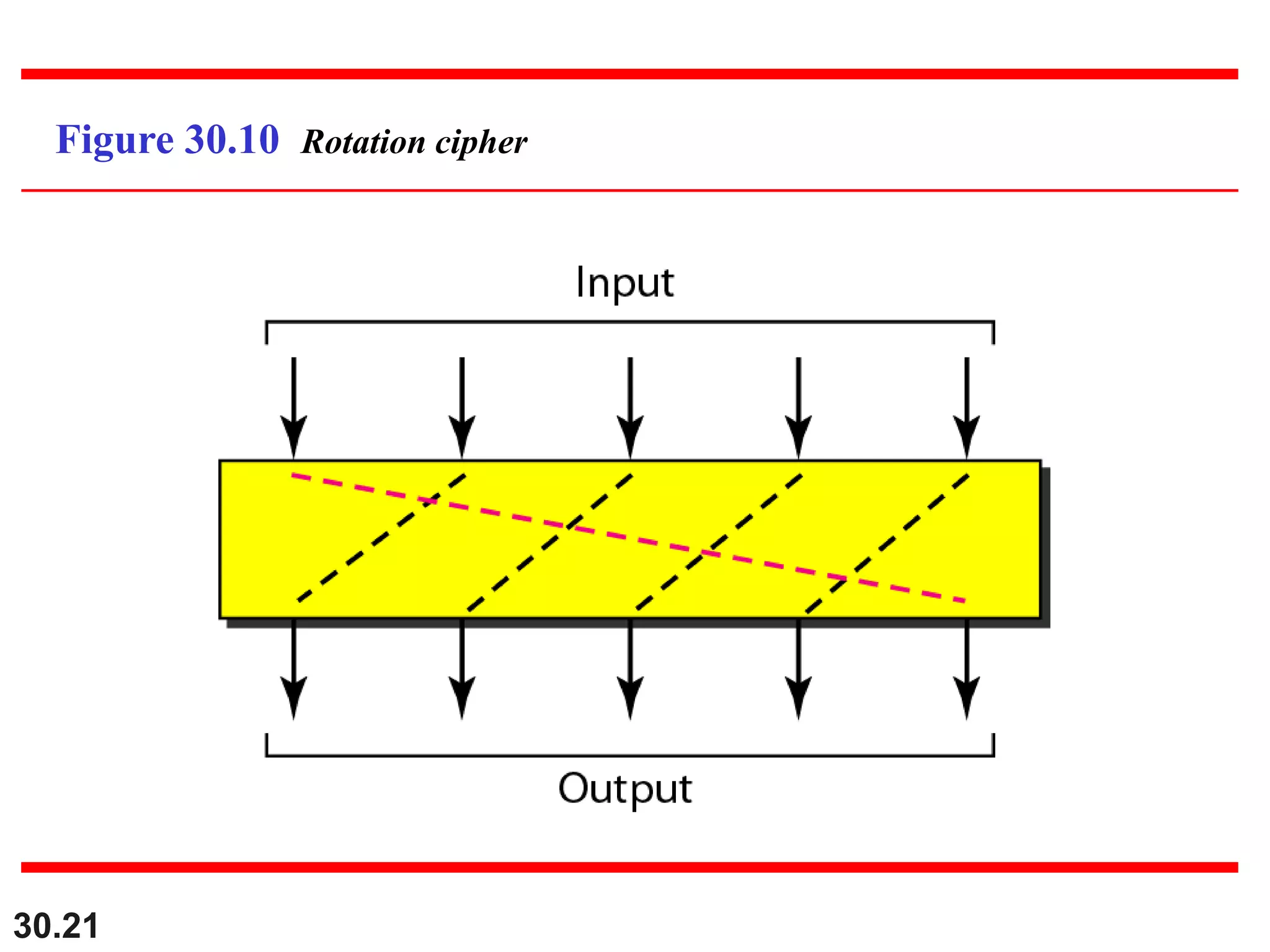
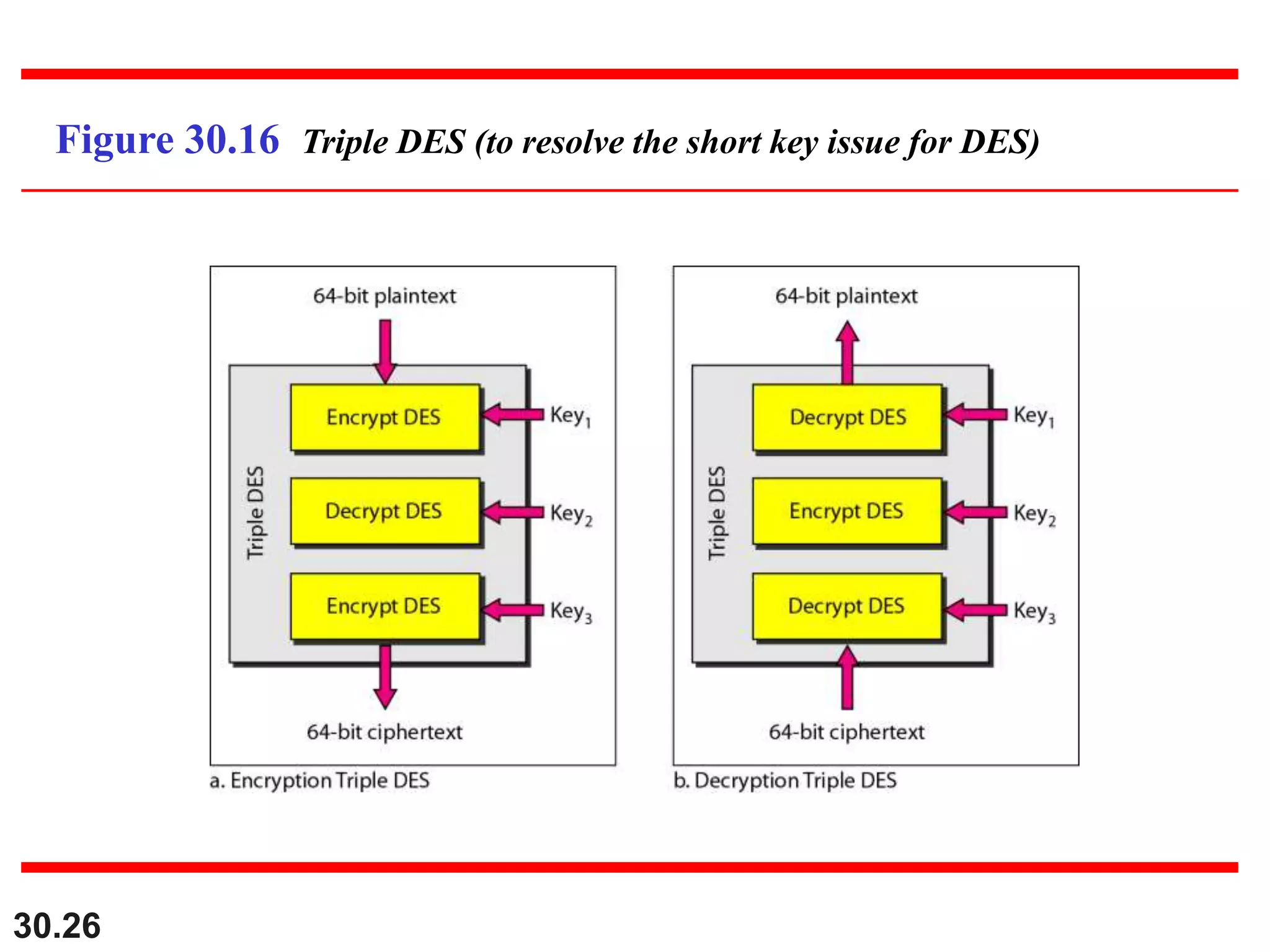
This document introduces cryptography and discusses symmetric-key and asymmetric-key cryptography. Symmetric-key cryptography uses the same key for encryption and decryption, while asymmetric-key cryptography uses two keys: a private key and a public key. Traditional ciphers like the shift cipher and transposition cipher are described. Modern symmetric ciphers include the XOR cipher, rotation cipher, and DES. Asymmetric ciphers like RSA are also introduced, which use a public key and private key based on large prime numbers. AES is presented as the replacement for the DES standard.