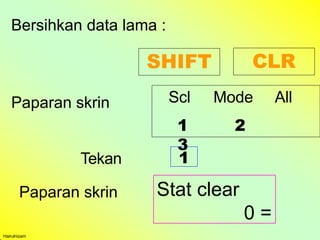
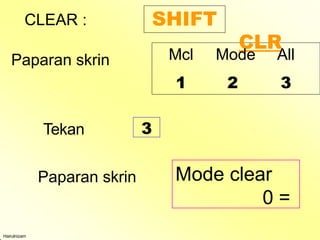
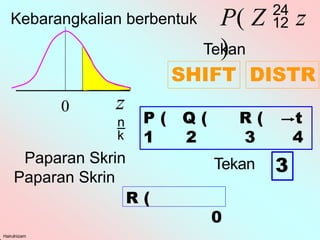
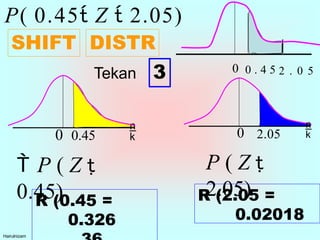
sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matematik. sebenarnya aku yang bersalah terhadap kecyaisna melalui kesipalan matemati