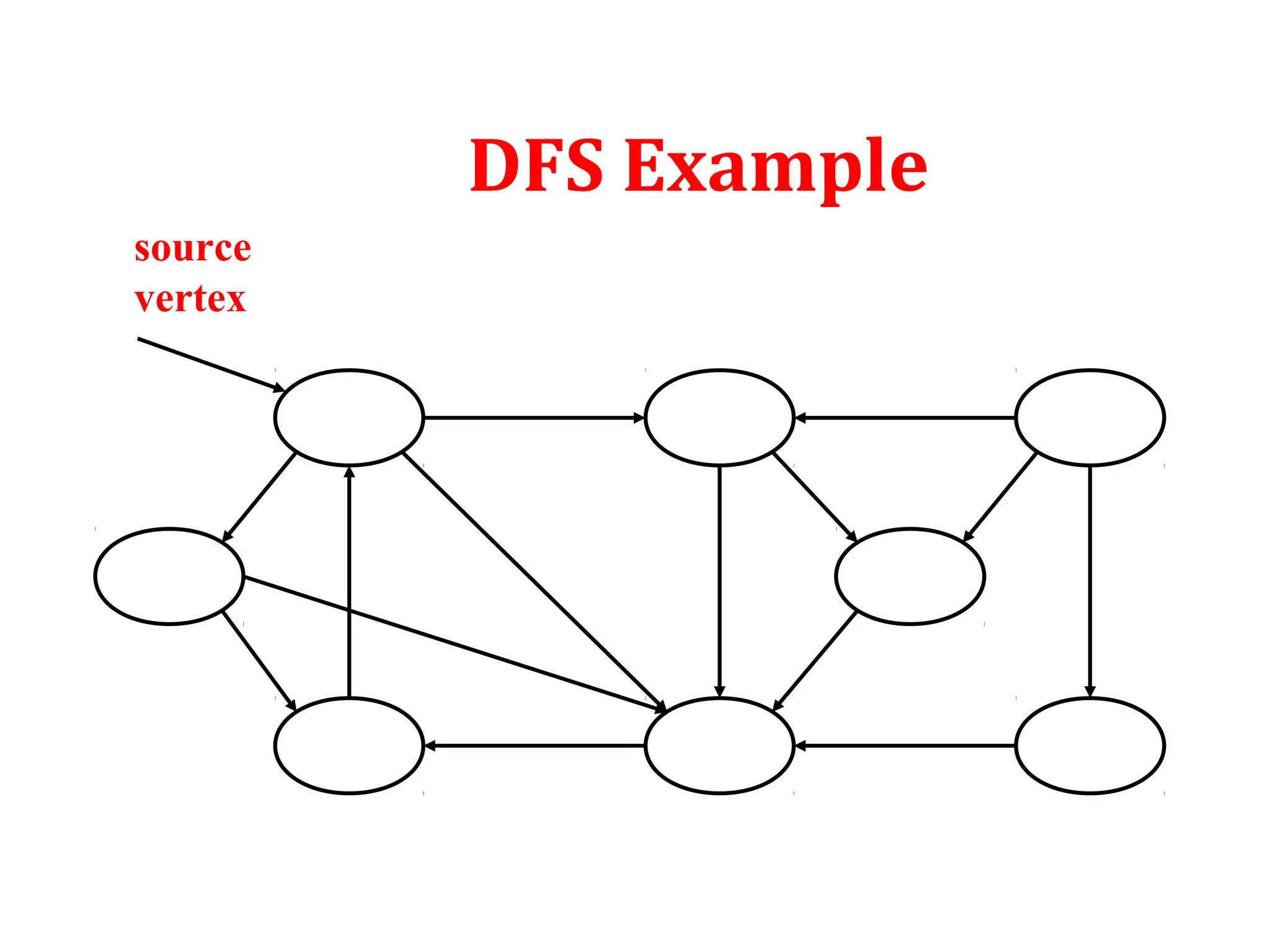
The document discusses two fundamental graph search algorithms: Breadth-First Search (BFS) and Depth-First Search (DFS). BFS systematically explores a graph level by level to find the shortest paths from a source vertex, while DFS explores as far as possible along branches before backtracking. Both algorithms utilize vertex coloring to keep track of their progress and have a time complexity of O(v + e), where v is the number of vertices and e is the number of edges.

1. Graph Algorithms-
BFS & DFS

2. Graph Search (traversal)
 How do we search a graph?
– At a particular vertices, where shall we go next?
 Two common framework:
 the depth-first search (DFS)
 the breadth-first search (BFS) and
 In DFS, go as far as possible along a single path until reach
a dead end (a vertex with no edge out or no neighbor
unexplored) then backtrack
 In BFS, one explore a graph level by level away (explore
all neighbors first and then move on)

3. Breadth First Search
• Given a graph G=(V, E) and a distinguished source vertex
s. Breadth first search systematically explores the edges
of graph G to discover every vertex that is reachable
from s.
• The algorithm finds the distance of each vertex from
the source vertex. If finds the minimum distance
(smallest number of edges) from source s to each
reachable vertex.
• It also produces a breadth first tree with root s that
contains all reachable vertices.
• Breadth first search is so named because the algorithm
discovers all vertices at distance k from s before
discovering any vertices at distance k+1

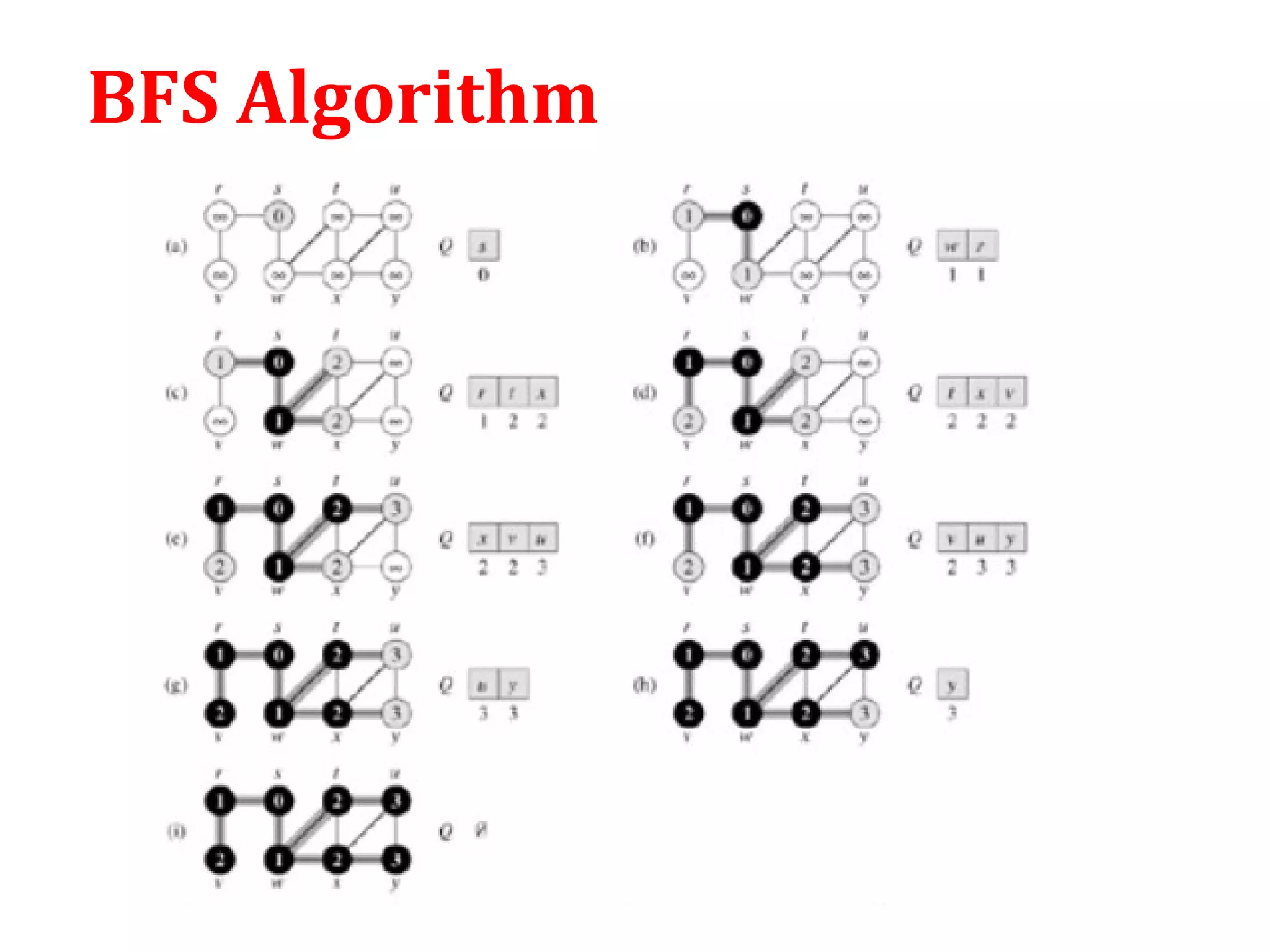
4. Breadth First Search
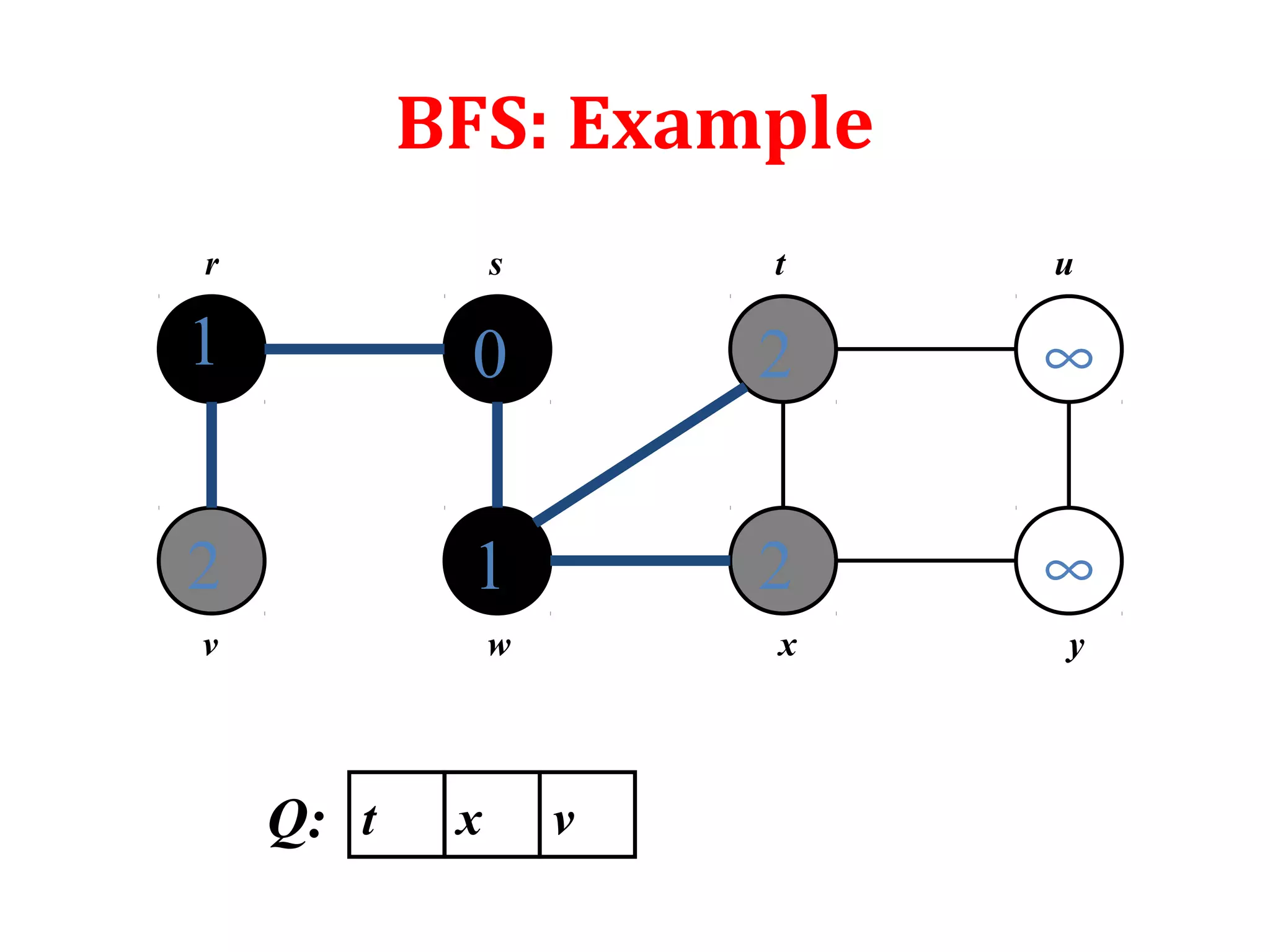
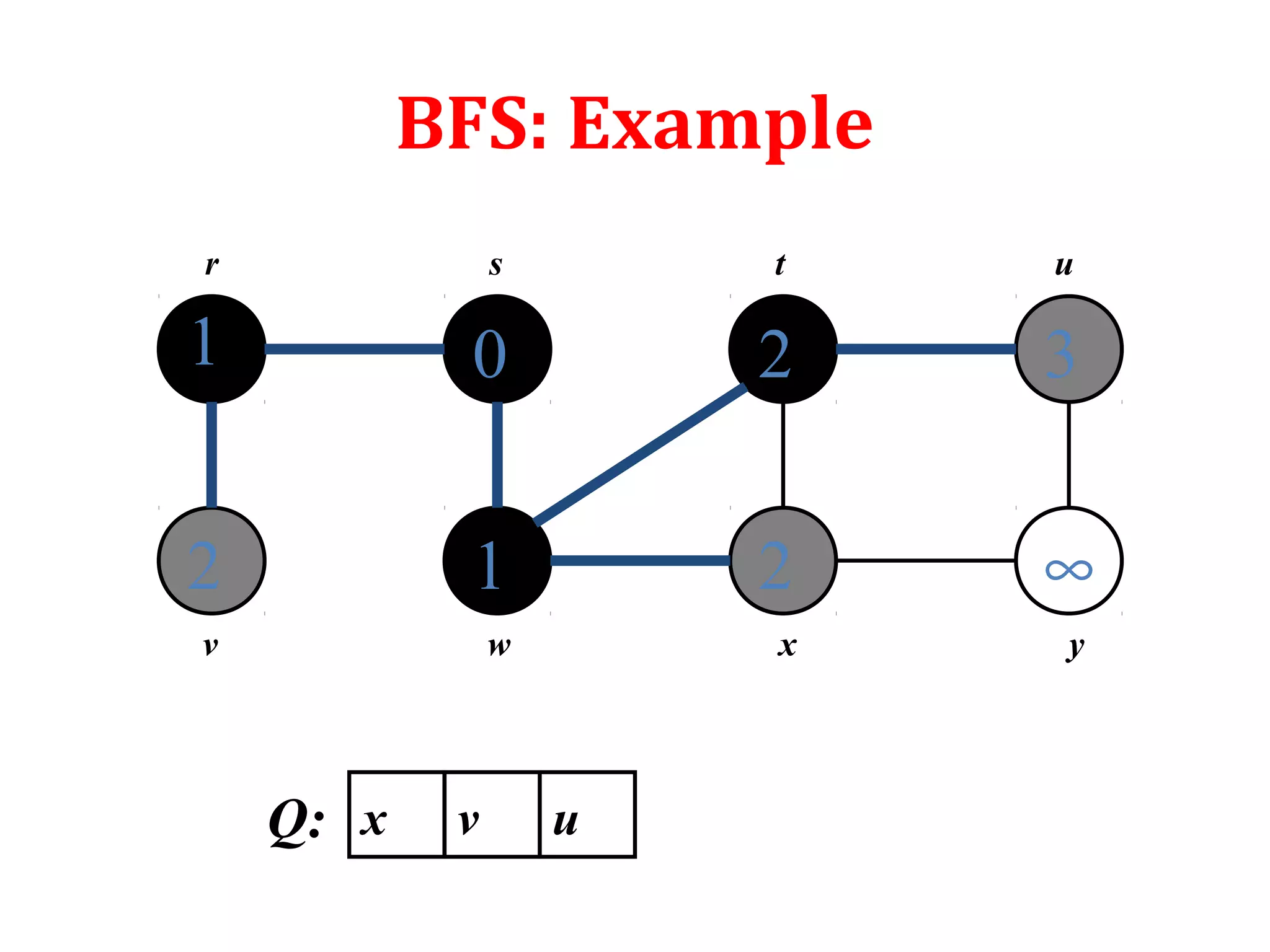
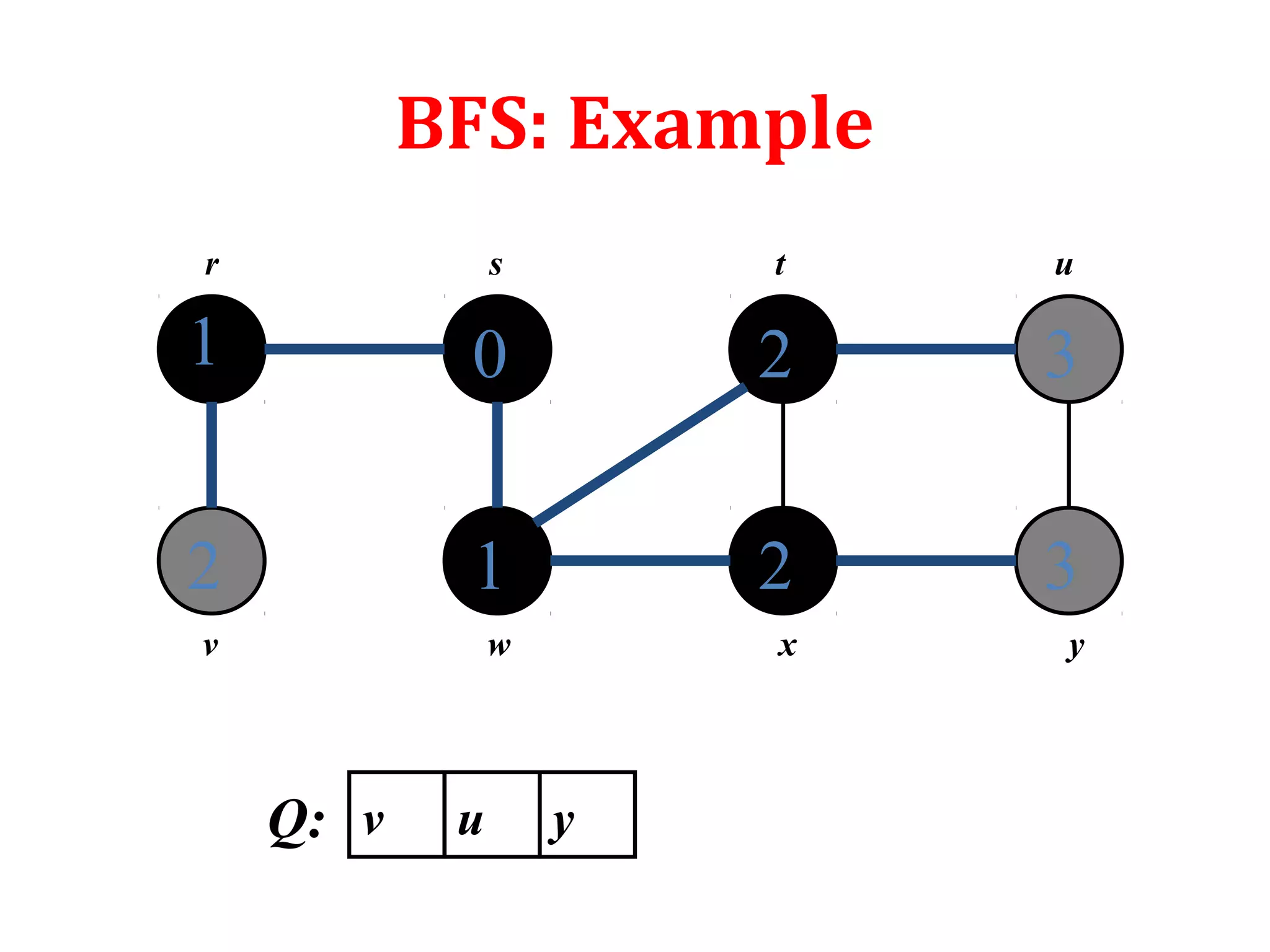
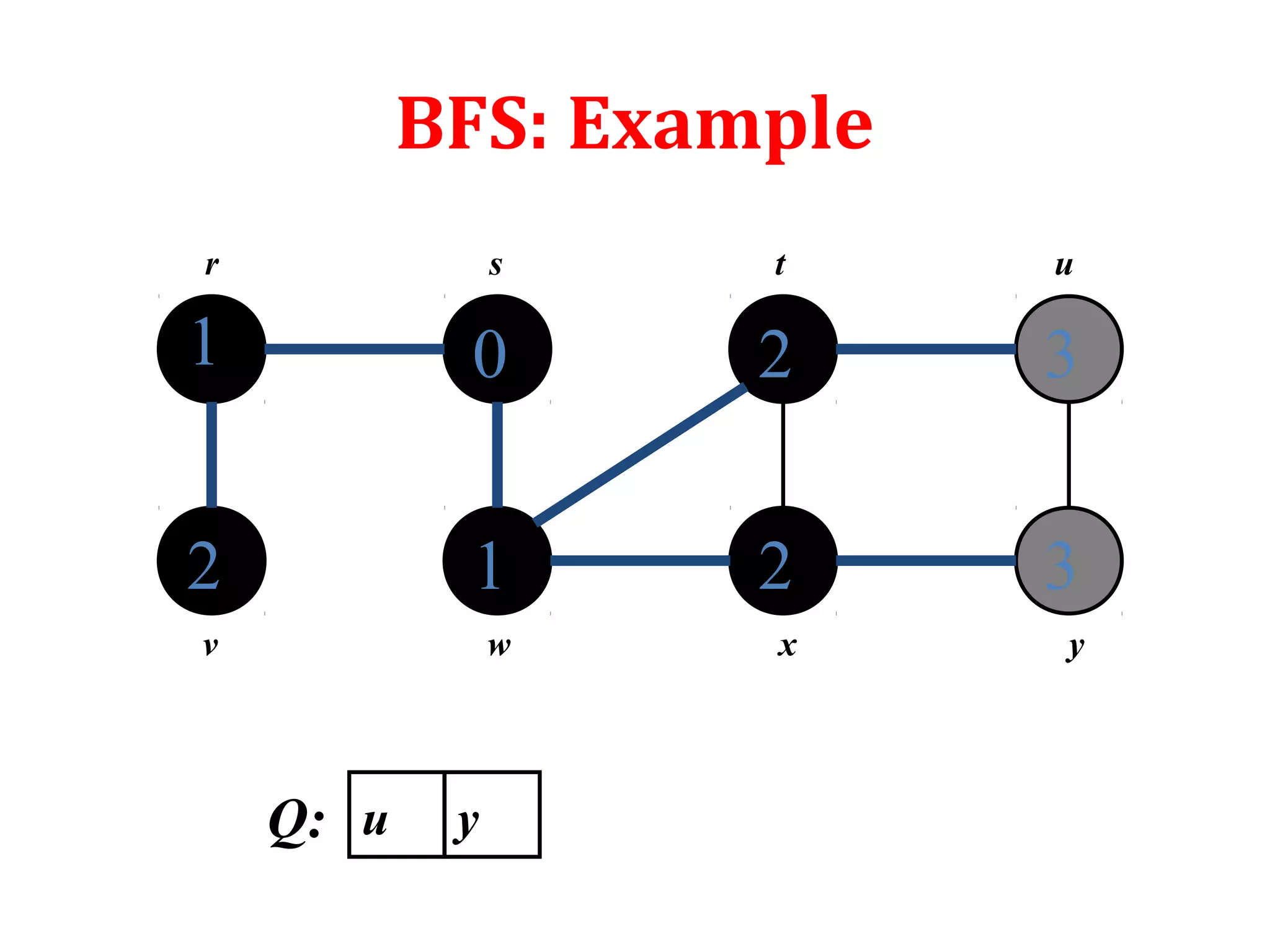
• It works for both directed and undirected graphs
• To keep track of progress BFS colors each vertex white,
gray or black. All vertices start with white and may later
become gray and then black. White color denote
undiscovered vertex. Gray and black denote discovered
vertex. While gray denote discovered vertex which is still
under process or in the queue. And black denote
completely processed and discovered vertex.
• d[u] denotes the distance of vertex u from source s
• (u) denotes the parent of vertexᴨ u
• Adj[u] denotes the adjacent vertices of u

5. BFS Algorithm

6. BFS Algorithm

7. BFS: Example
∞
∞
∞
∞
∞
∞
∞
∞
r s t u
v w x y

8. ∞
∞
0
∞
∞
∞
∞
∞
r s t u
v w x y
sQ:
BFS: Example

9. 1
∞
0
1
∞
∞
∞
∞
r s t u
v w x y
wQ: r
BFS: Example

10. BFS: Example
1
∞
0
1
2
2
∞
∞
r s t u
v w x y
rQ: t x

11. BFS: Example
1
2
0
1
2
2
∞
∞
r s t u
v w x y
Q: t x v

12. BFS: Example
1
2
0
1
2
2
3
∞
r s t u
v w x y
Q: x v u

13. BFS: Example
1
2
0
1
2
2
3
3
r s t u
v w x y
Q: v u y

14. BFS: Example
1
2
0
1
2
2
3
3
r s t u
v w x y
Q: u y

15. BFS: Example
1
2
0
1
2
2
3
3
r s t u
v w x y
Q: y

16. BFS: Example
1
2
0
1
2
2
3
3
r s t u
v w x y
Q: Ø

17. BFS: Time Complexity
 Queuing time is O(V) and scanning all edges
requires O(E)
 Overhead for initialization is O (V)
 So, total running time is O(V+E)

18. Analysis of Time Complexity
 BFS takes O(V) time for initialization
 The operations of enqueuing and dequeuing take O(1) time
for each vertex. So the total time devoted to queue
operation for v vertices is O(V).
 Now the adjacency list of each vertex is scanned only when
the vertex is dequeued. Then the sum of the lengths of all
the adjacency lists is (E). So the total time spent inɵ
scanning adjacency lists is O(E).
 So the total time complexity of BFS is O(V+E)

19. BFS: Application
• Shortest path problem

20. Depth First Search
 DFS, go as far as possible along a single path until it reaches
a dead end (that is a vertex with no edge out or no neighbor
unexplored) then backtrack
 As the name implies the DFS search deeper in the graph
whenever possible. DFS explores edges out of the most
recently discovered vertex v that still has unexplored edges
leaving it. Once all of v’s edges have been explored, the
search backtracks to explore edges leaving the vertex from
which v was discovered.

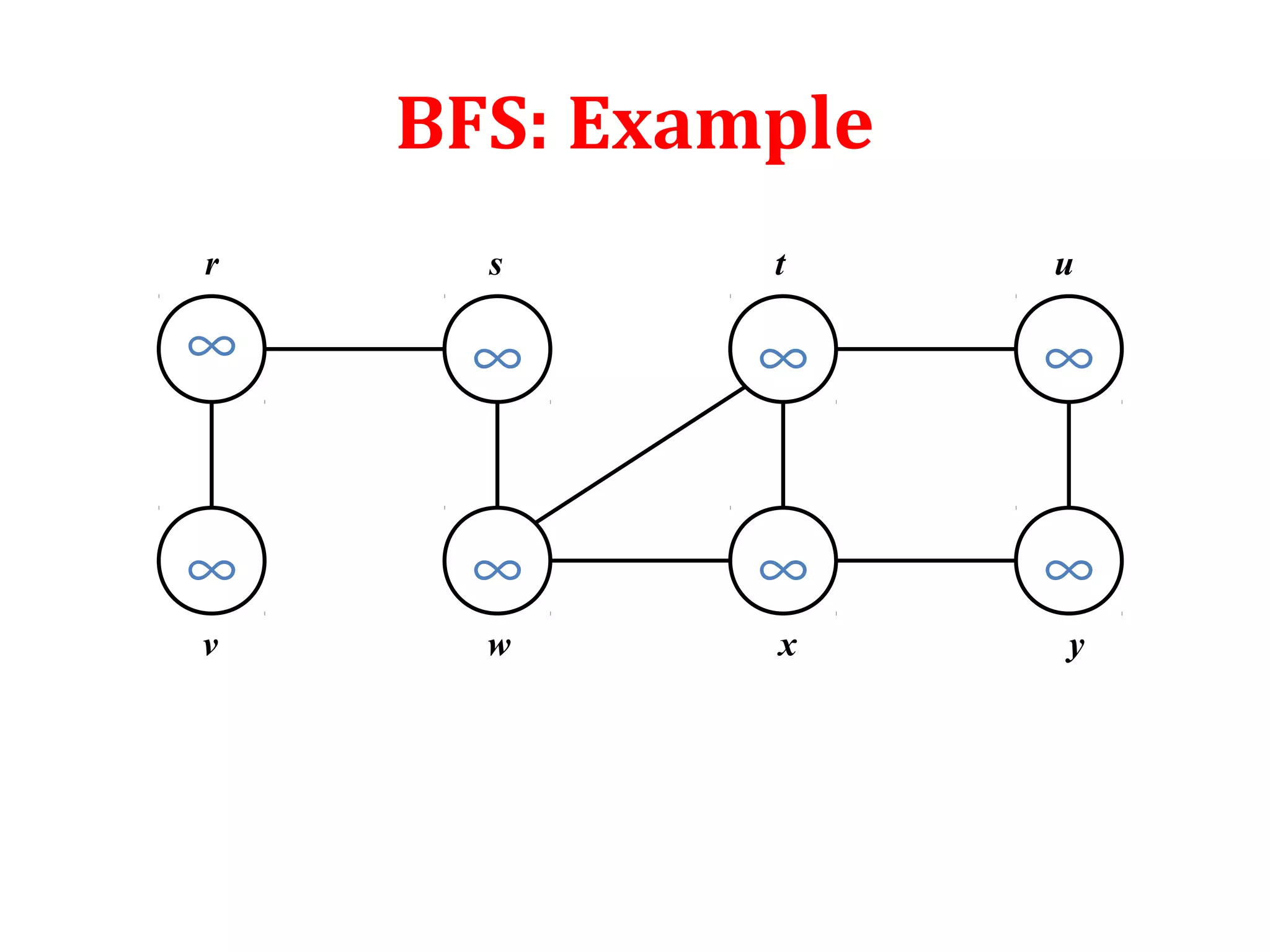
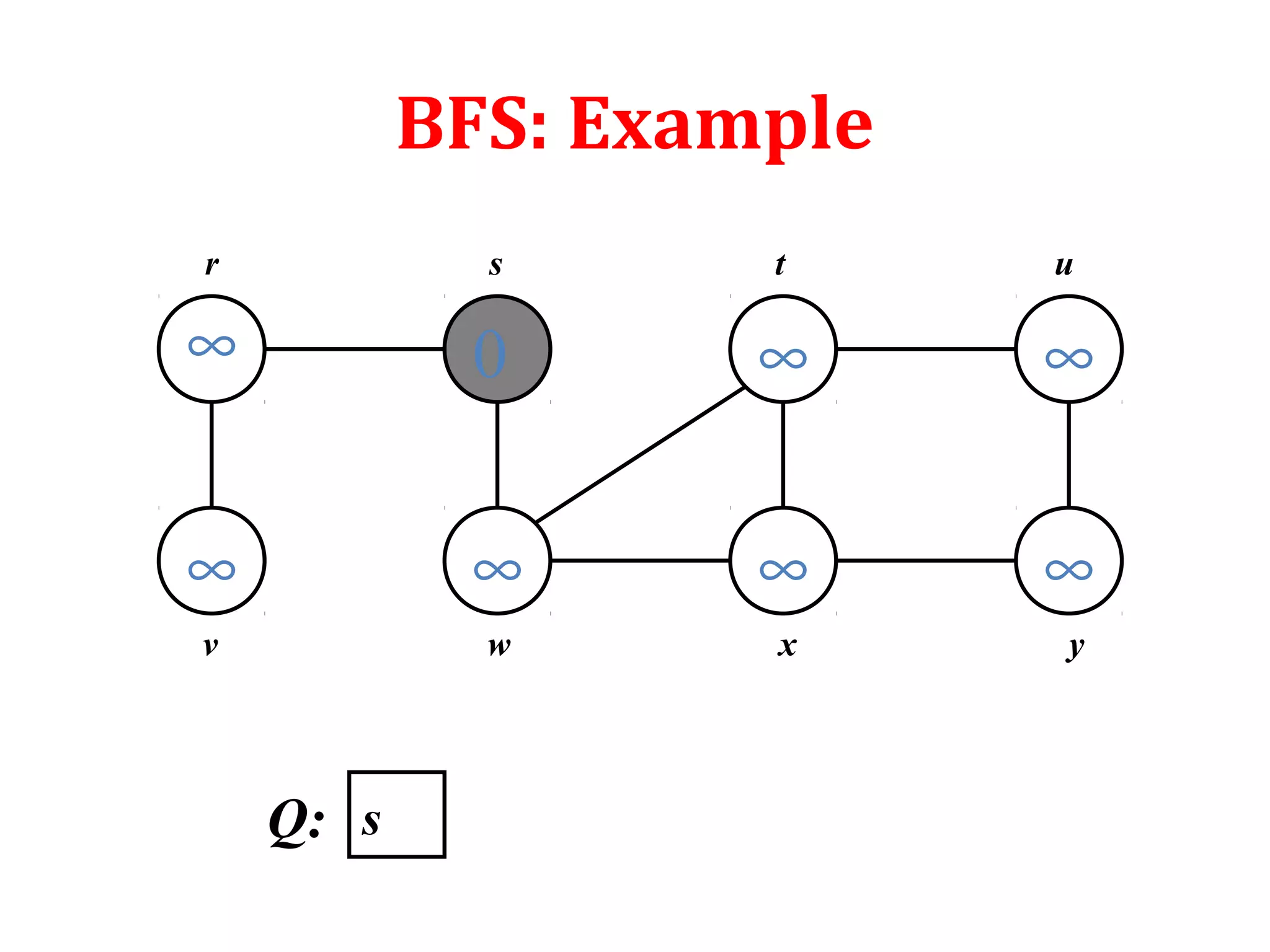
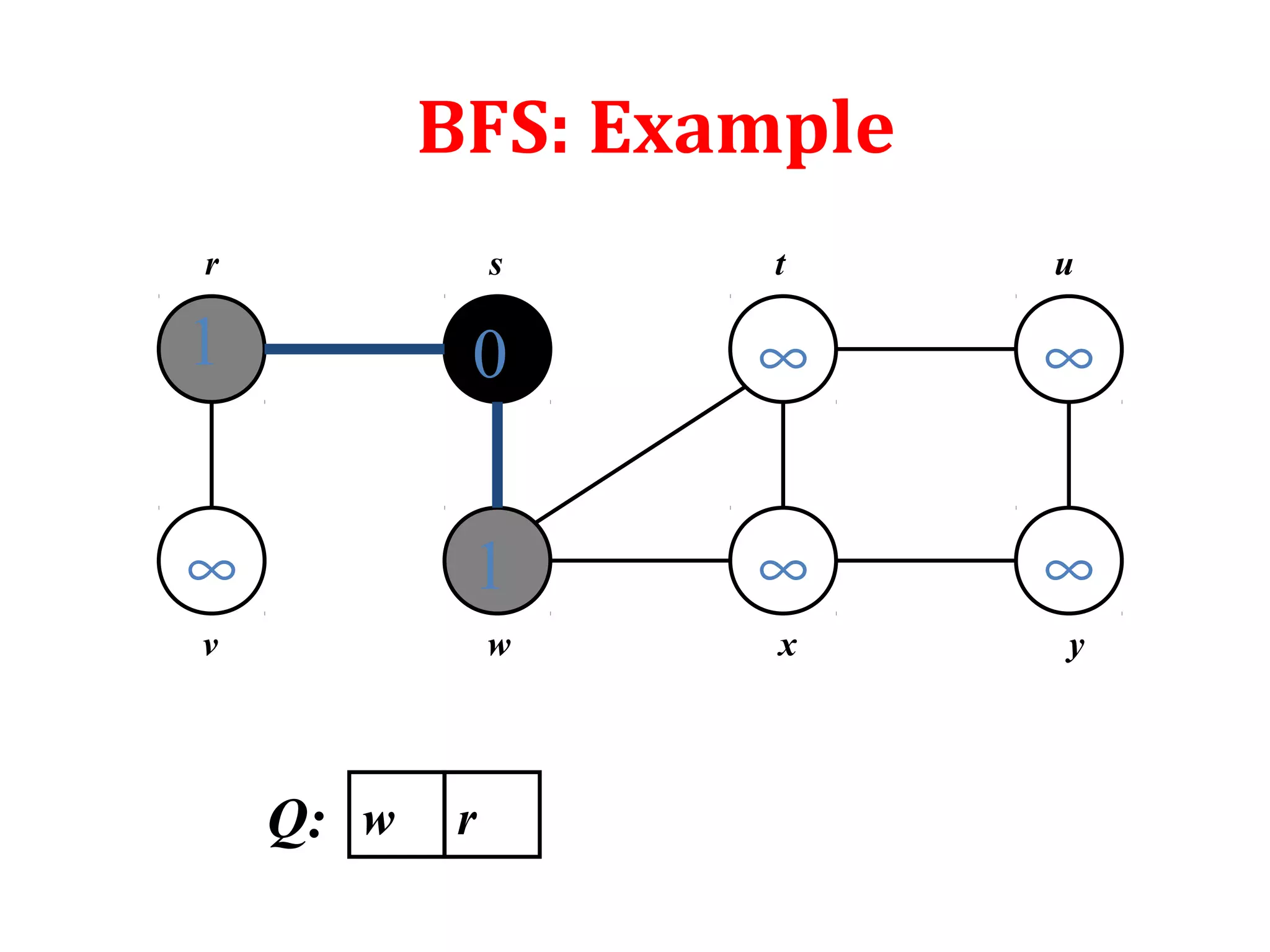
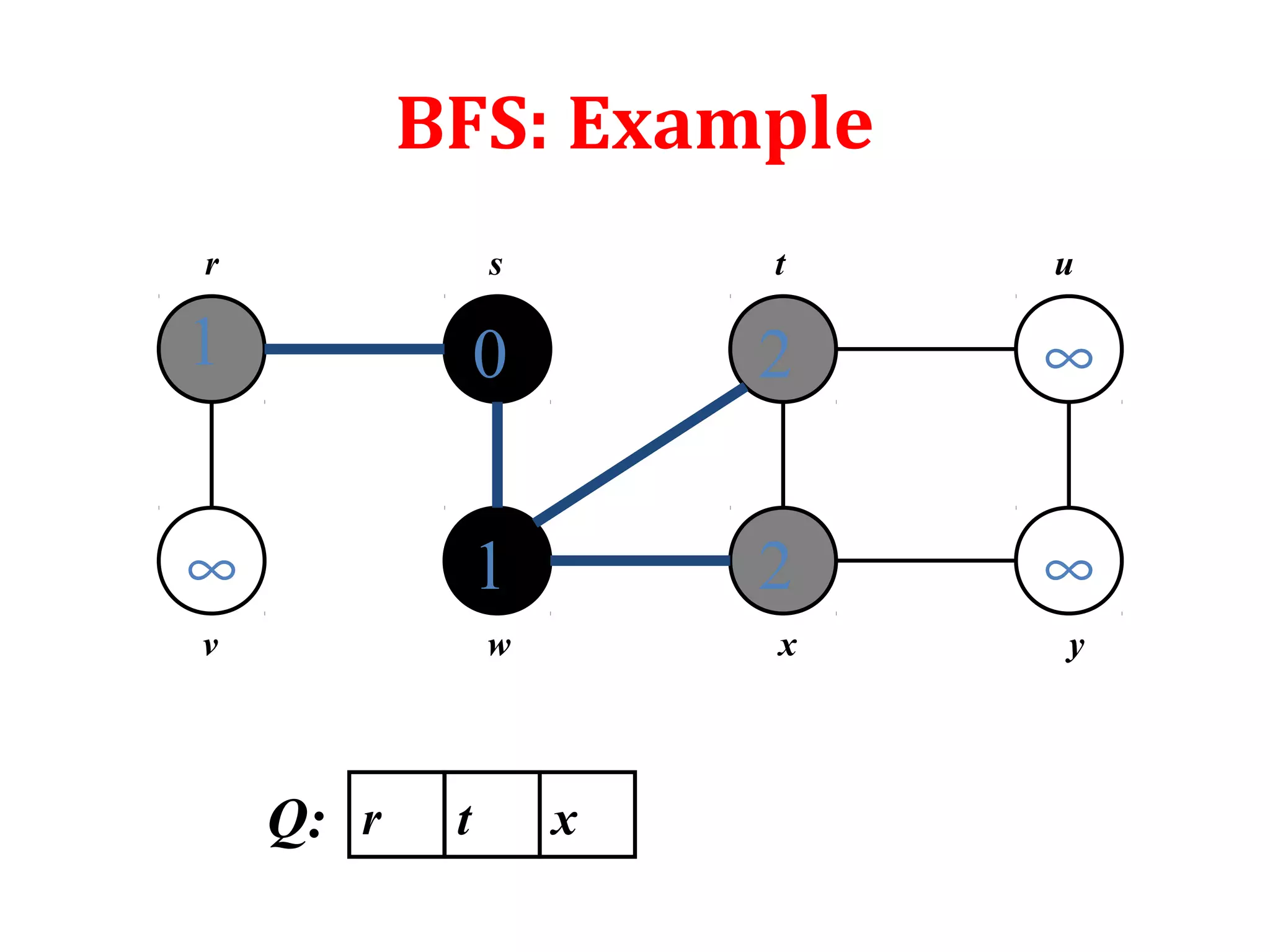
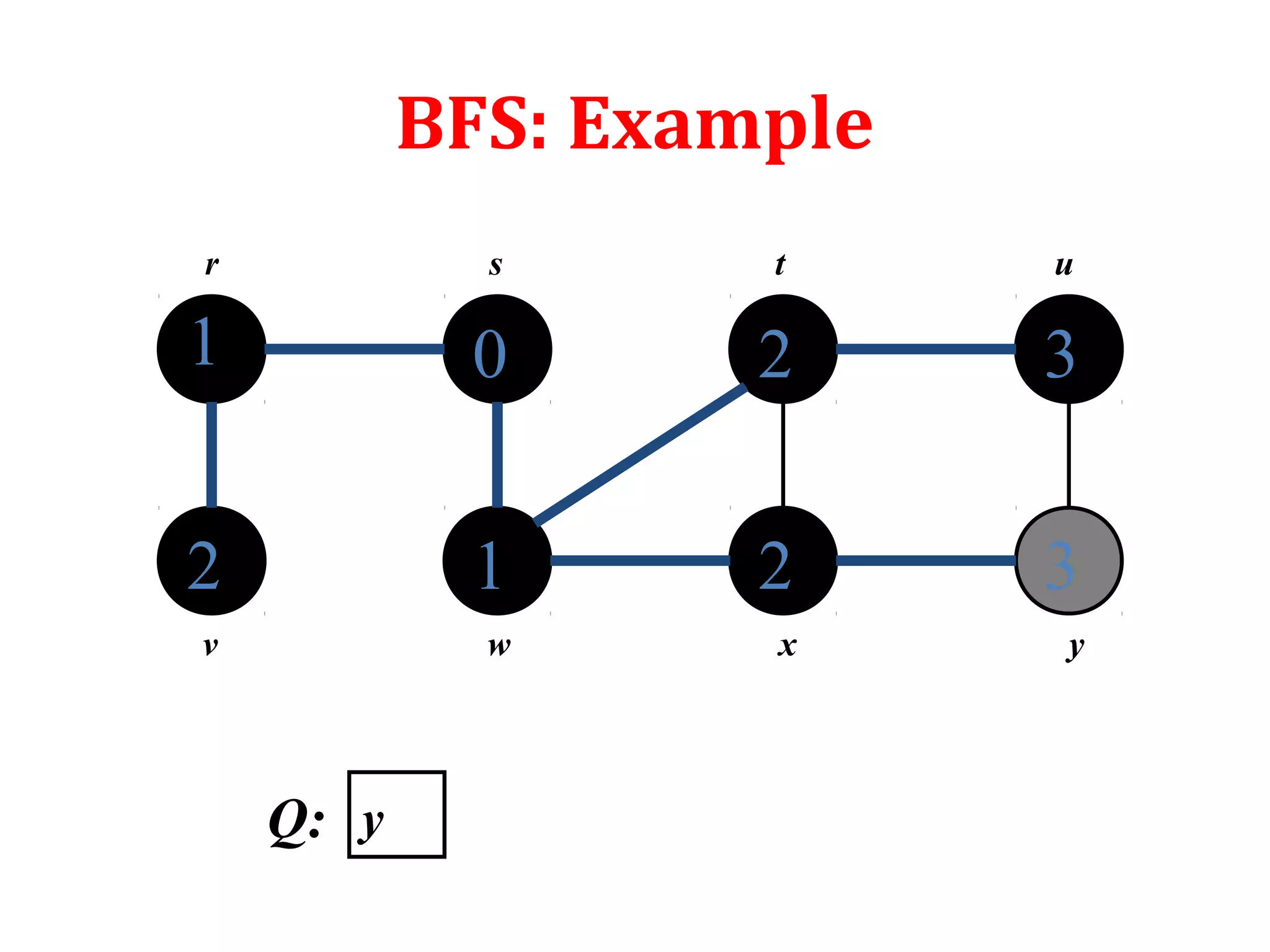
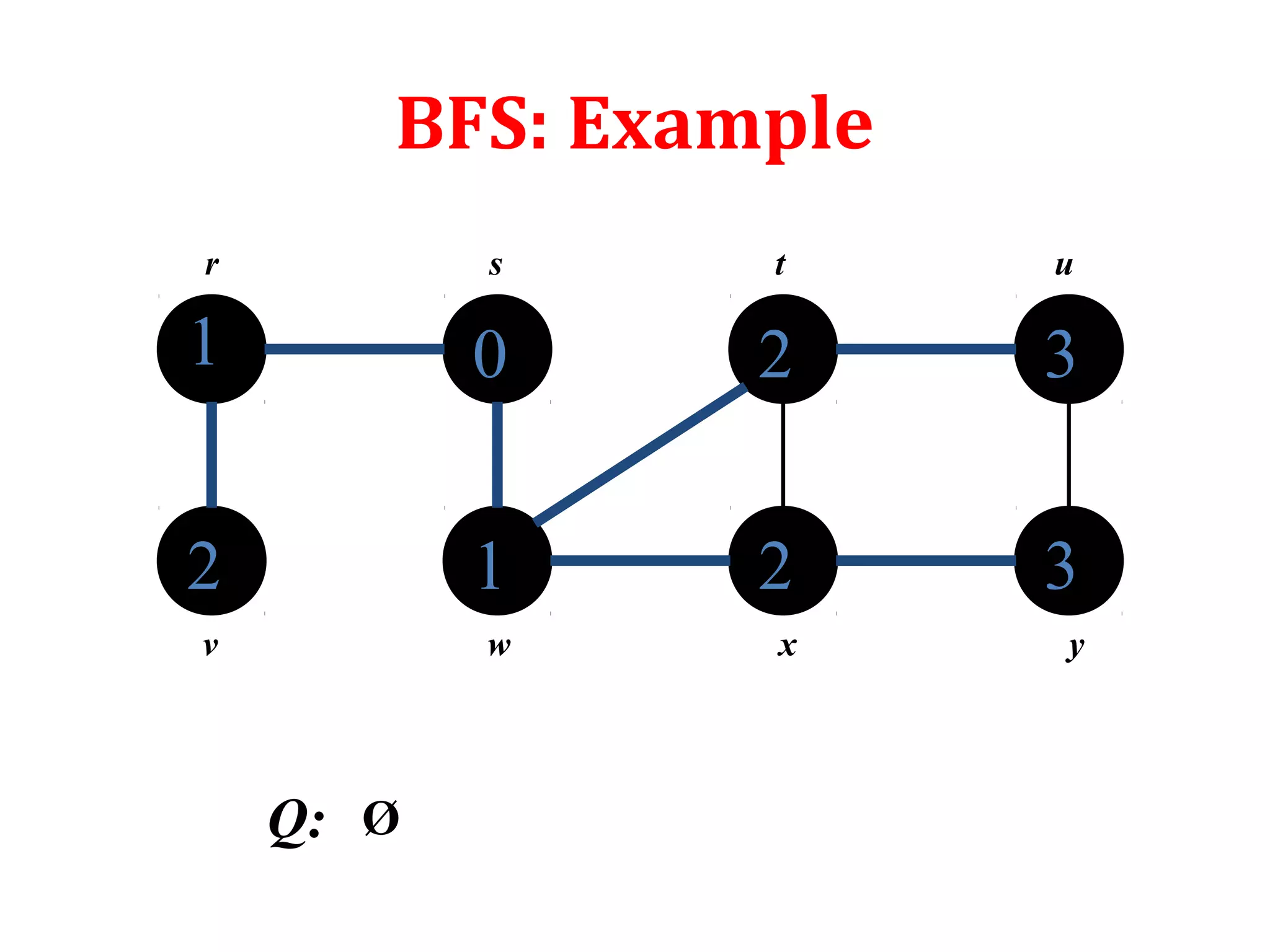
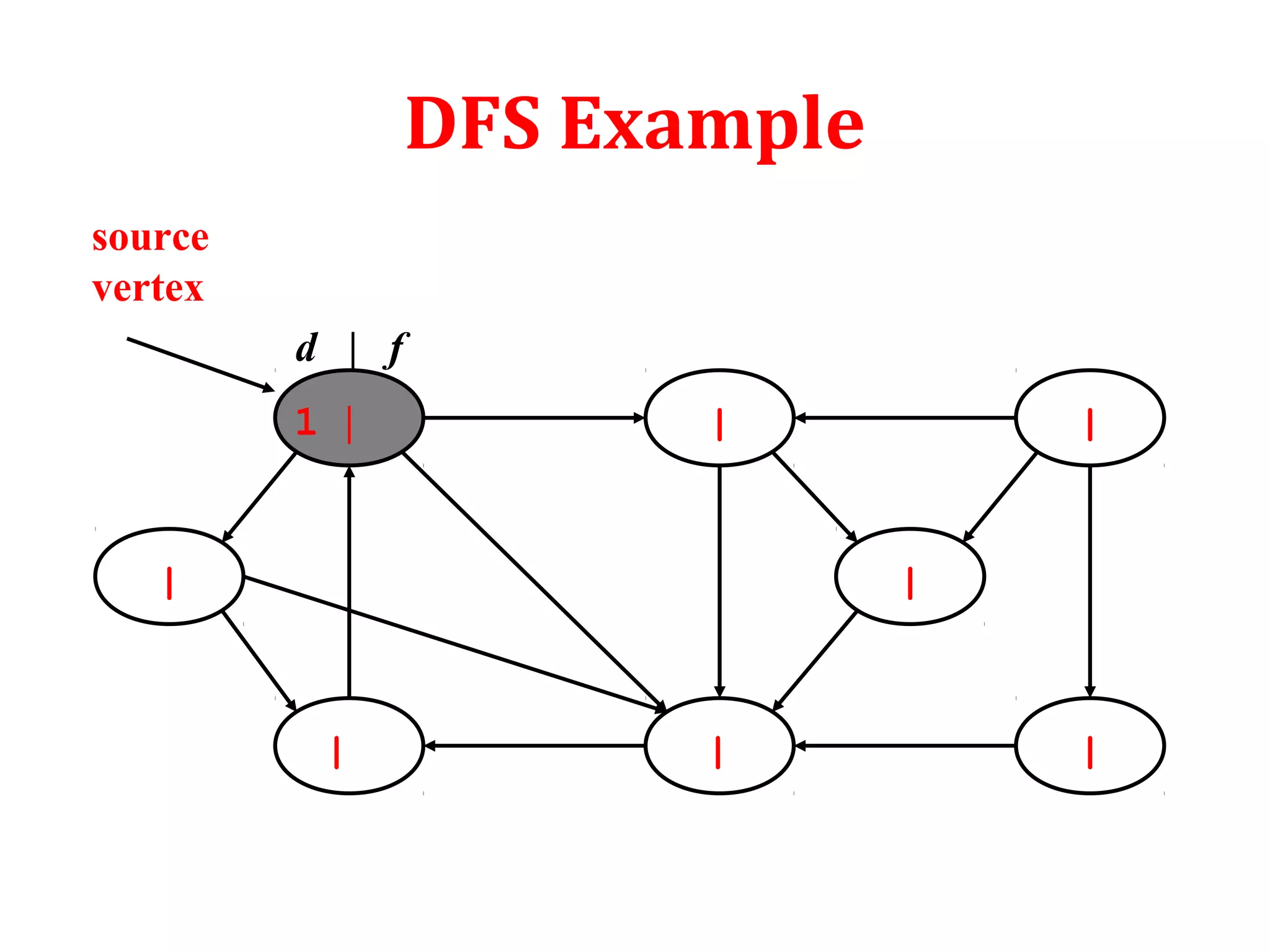
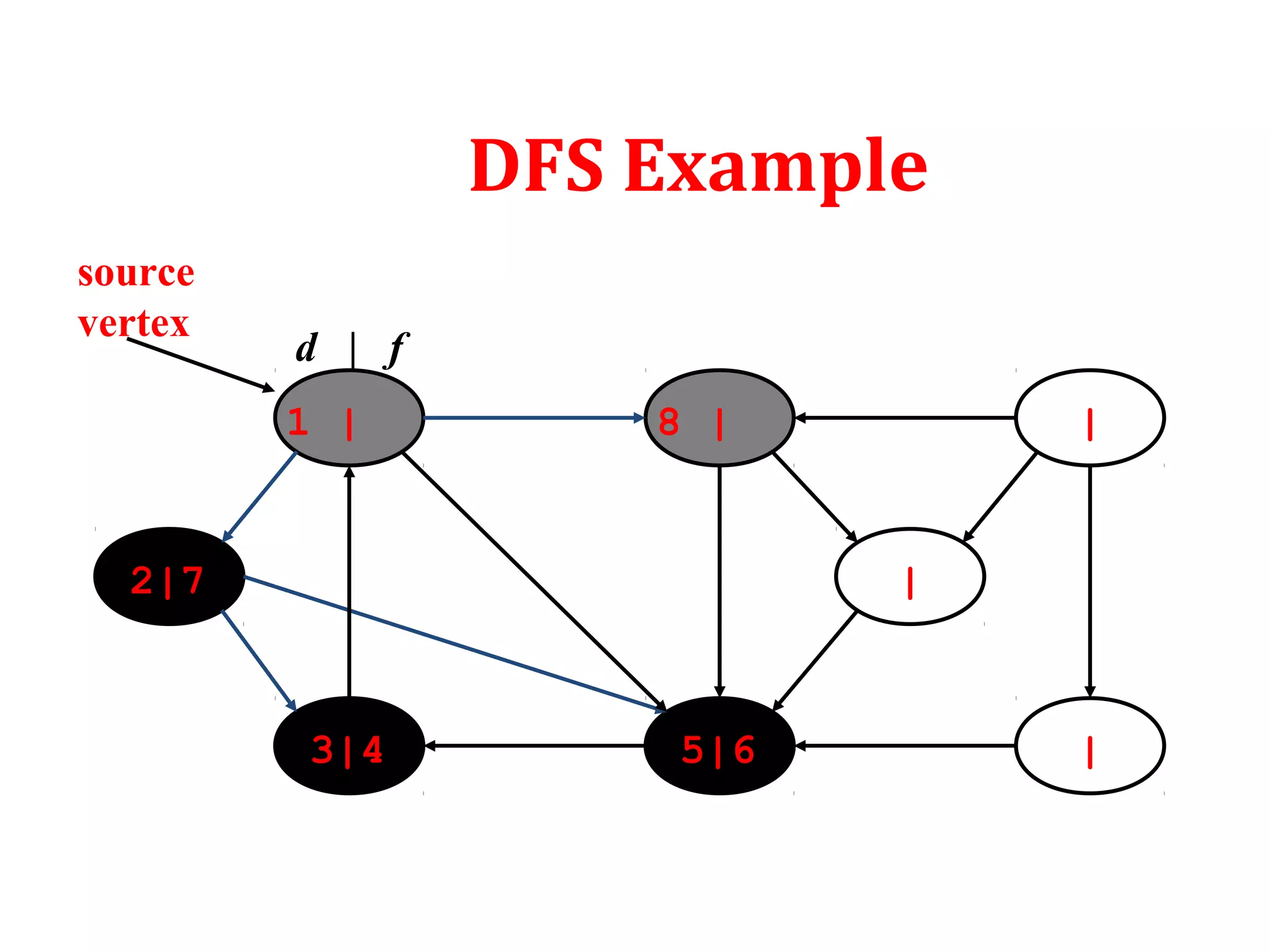
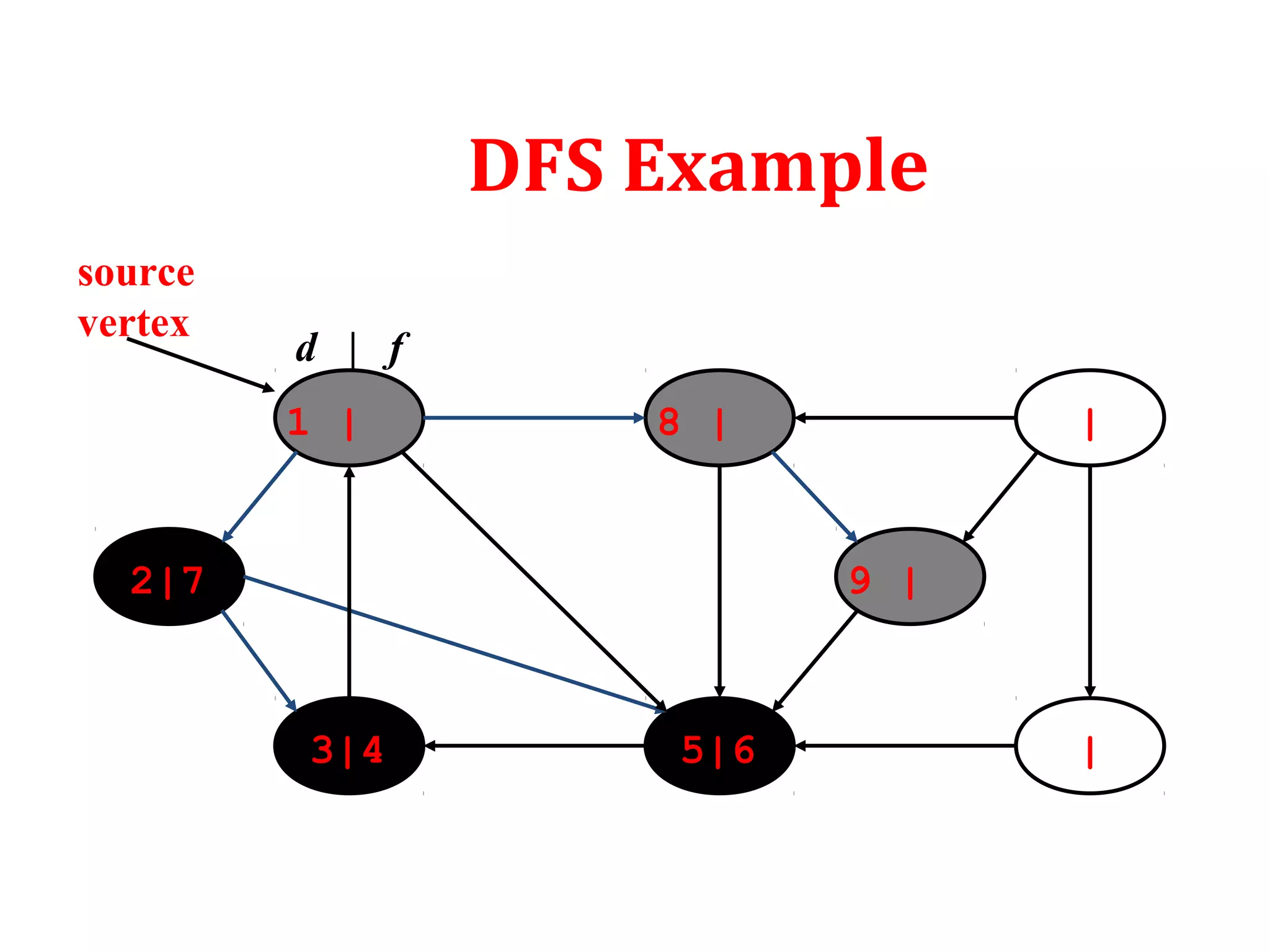
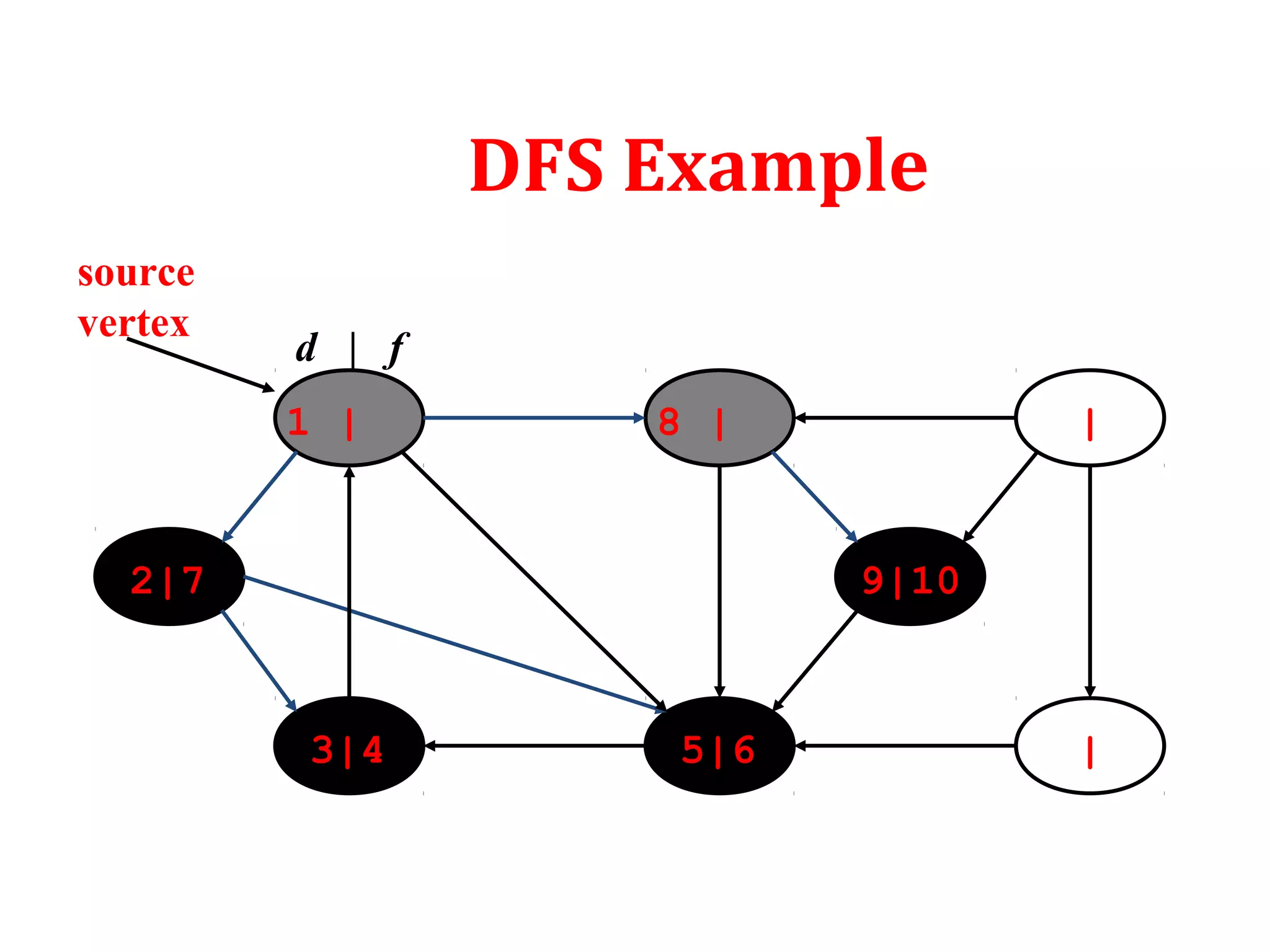
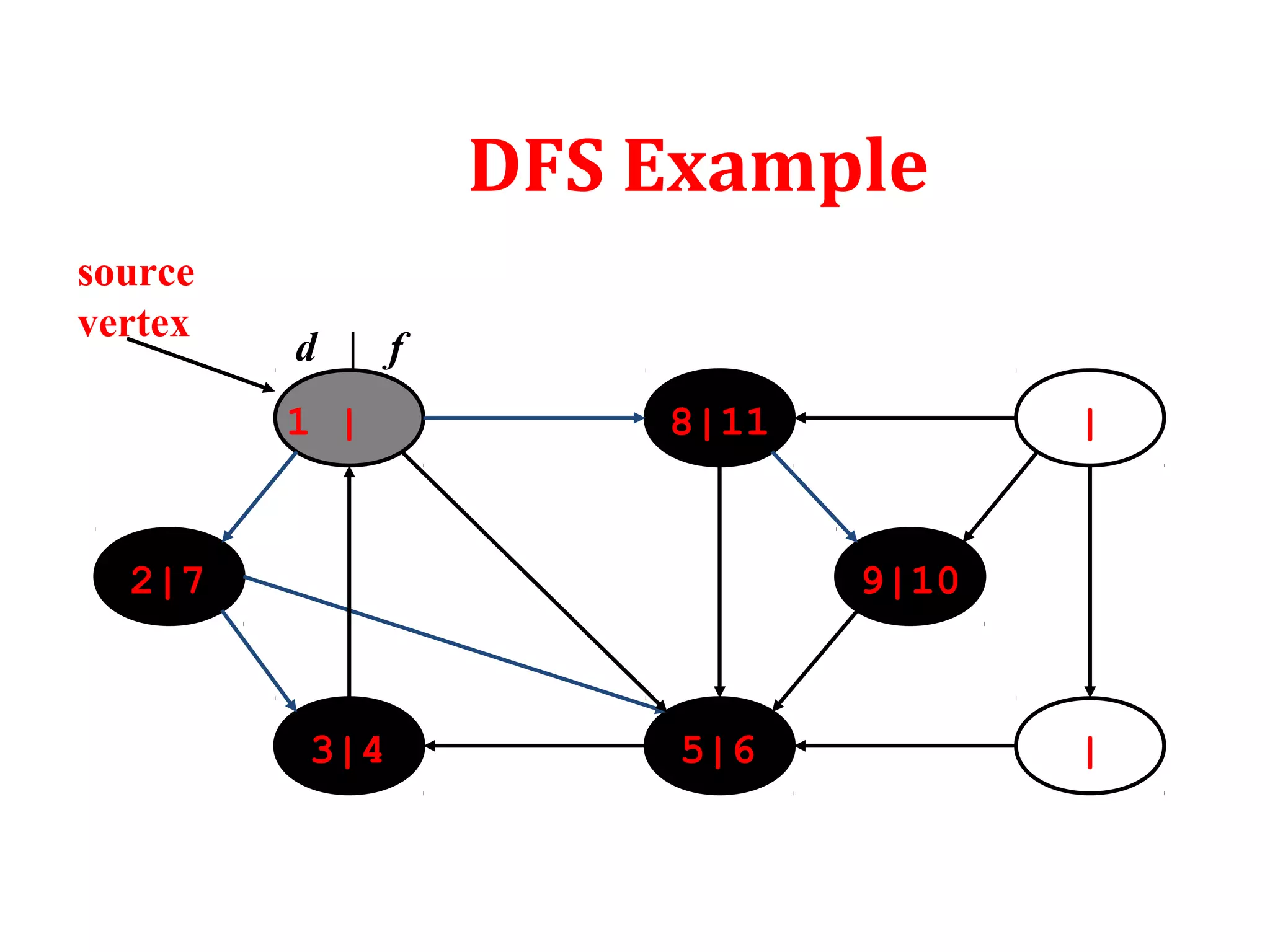
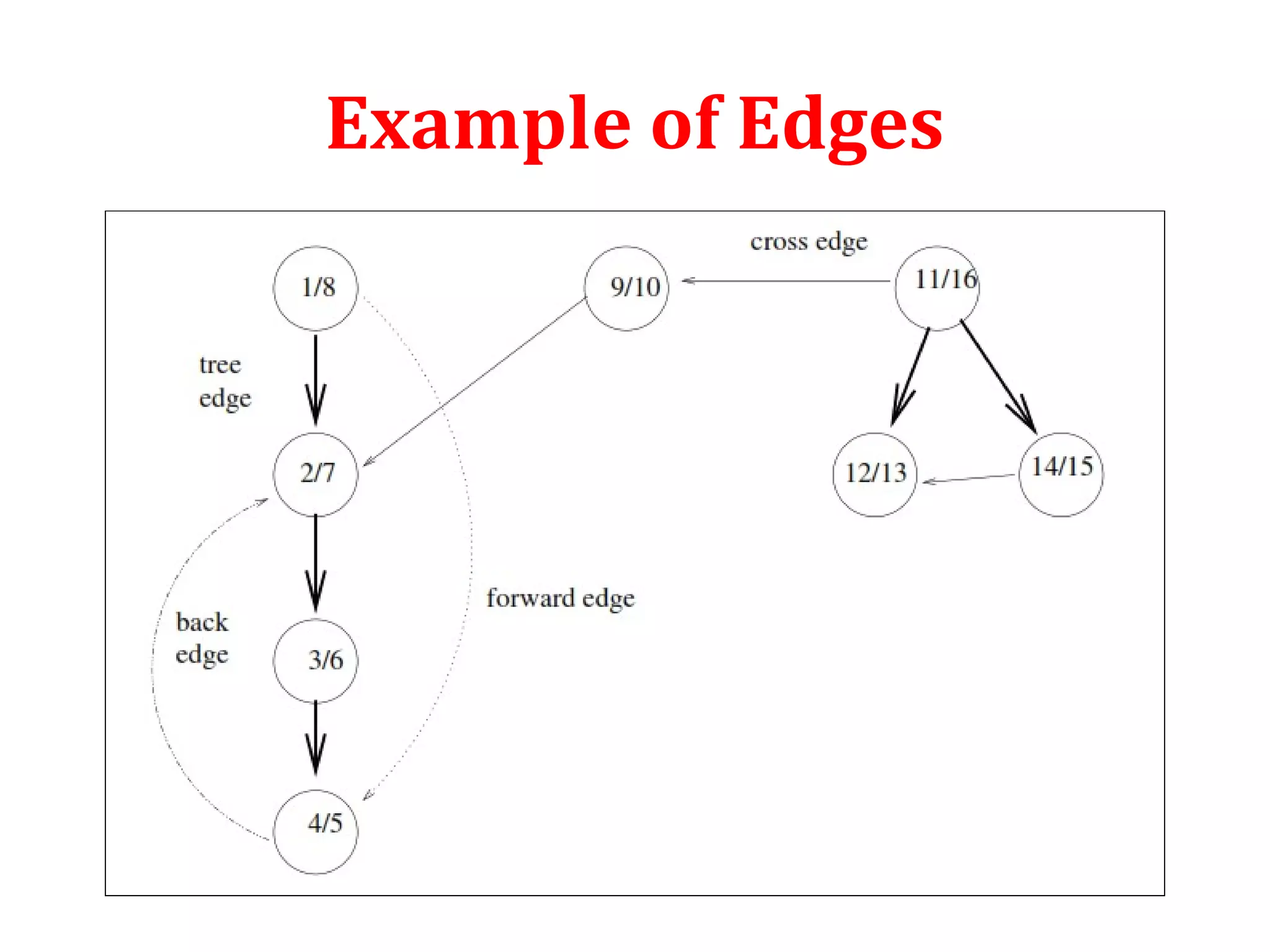
21. Depth First Search
 To keep track of progress DFS colors each vertex white, gray or
black. Initially all the vertices are colored white. Then they are
colored gray when discovered. Finally colored black when
finished.
 Besides creating depth first forest DFS also timestamps each
vertex. Each vertex goes through two time stamps:
 Discover time d[u]: when u is first discovered
 Finish time f[u]: when backtrack from u or finished u
 f[u] > d[u]

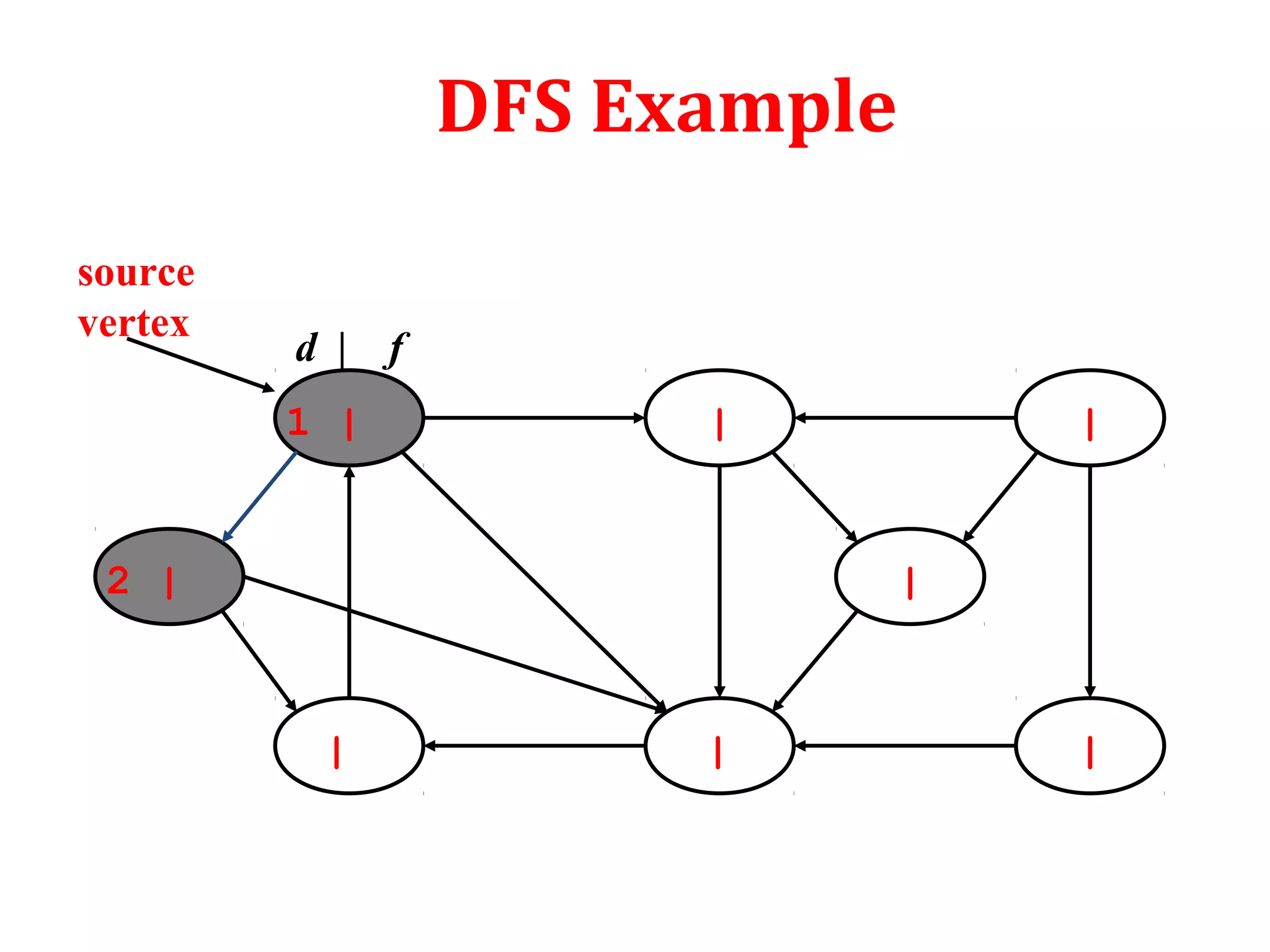
22. DFS: Algorithm
 DFS(G)
1. for each vertex u in G
2. color[u]=white
3. [u]=NILᴨ
4. time=0
5. for each vertex u in G
6. if (color[u]==white)
7. DFS-VISIT(G,u)

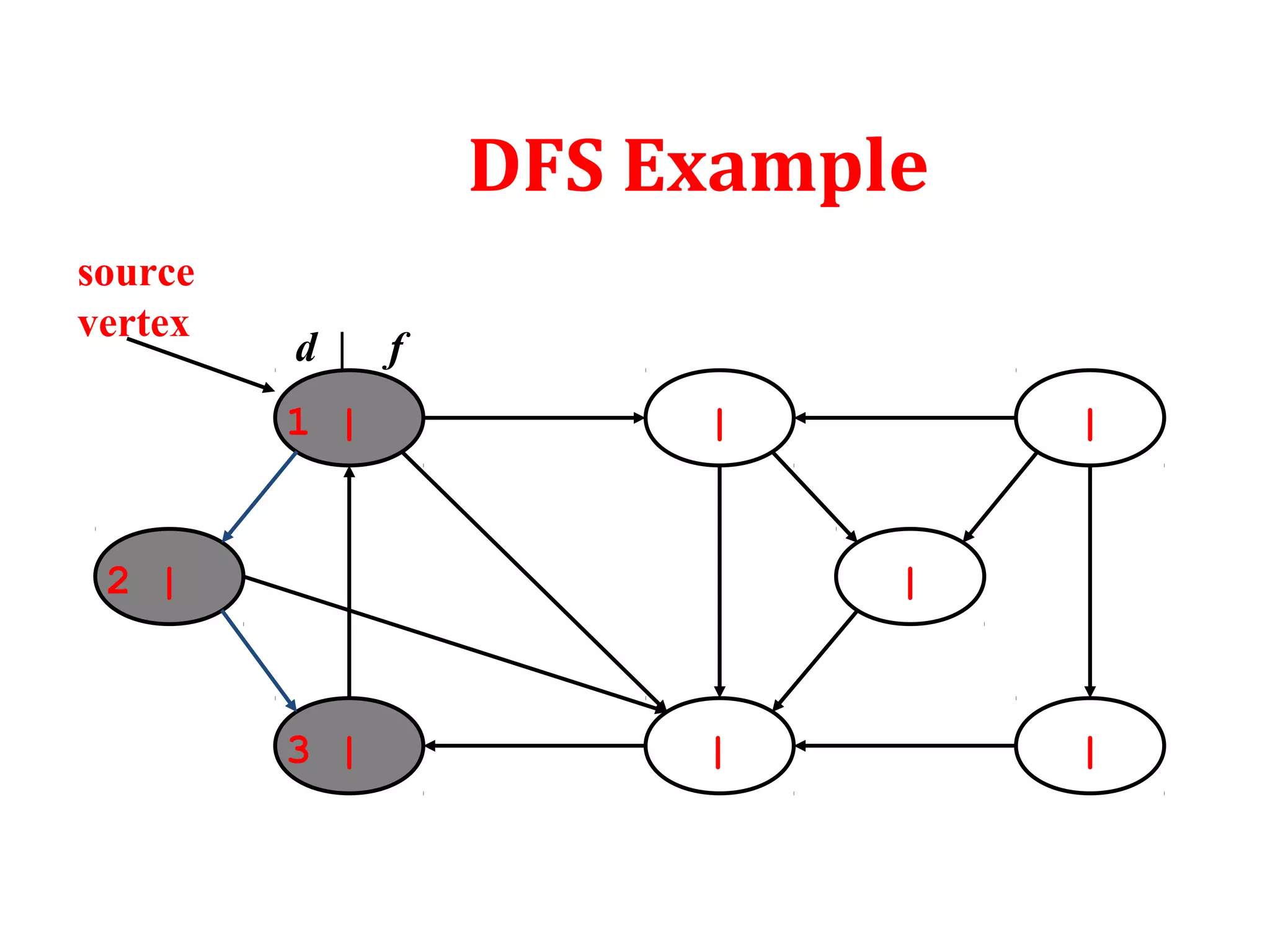
23. DFS-VISIT(u)
1. time = time + 1
2. d[u] = time
3. color[u]=gray
4. for each v € Adj(u) in G do
5. if (color[v] = =white)
6. [v] = u;ᴨ
7. DFS-VISIT(G,v);
8. color[u] = black
9. time = time + 1;
10. f[u]= time;
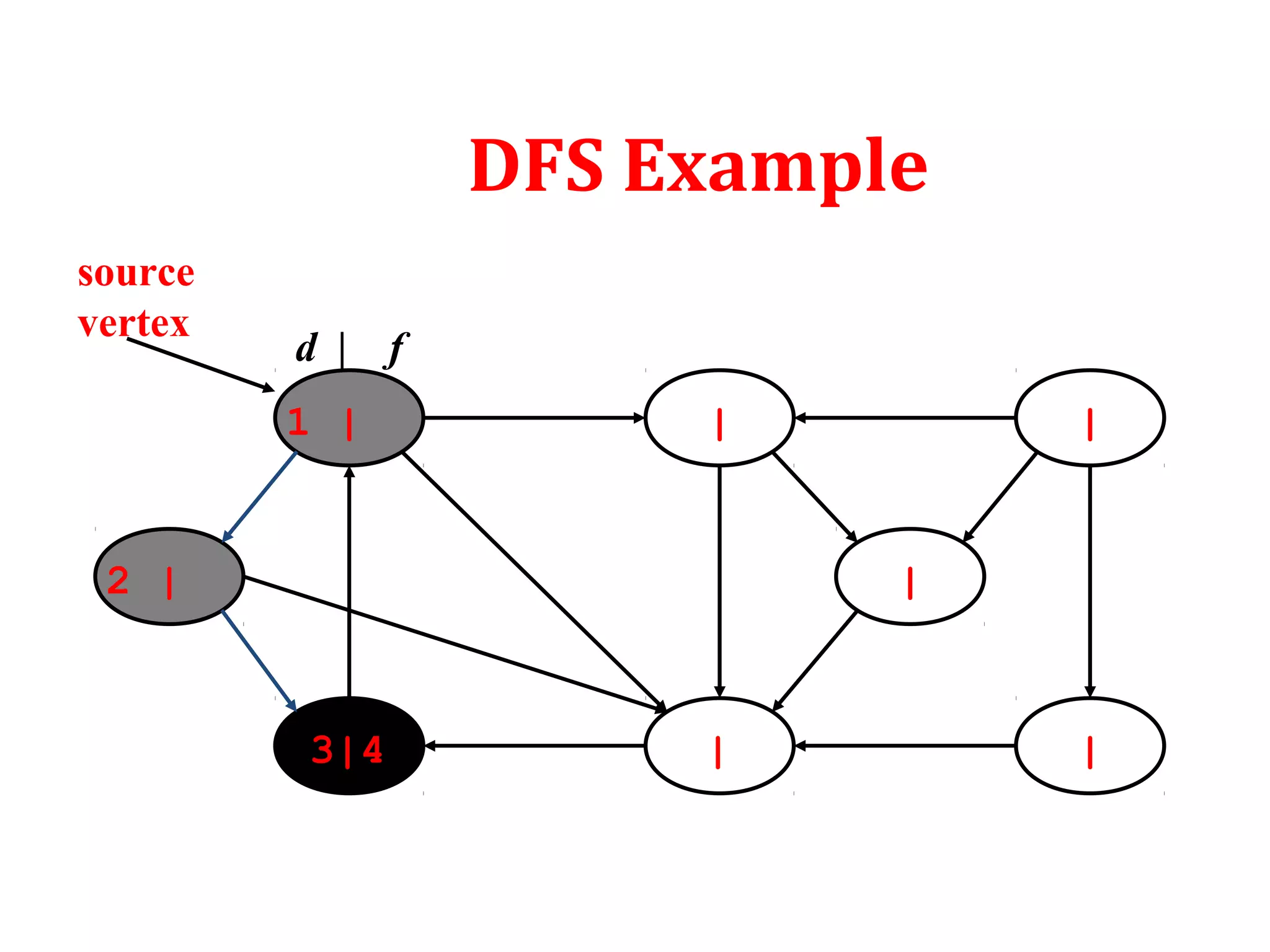
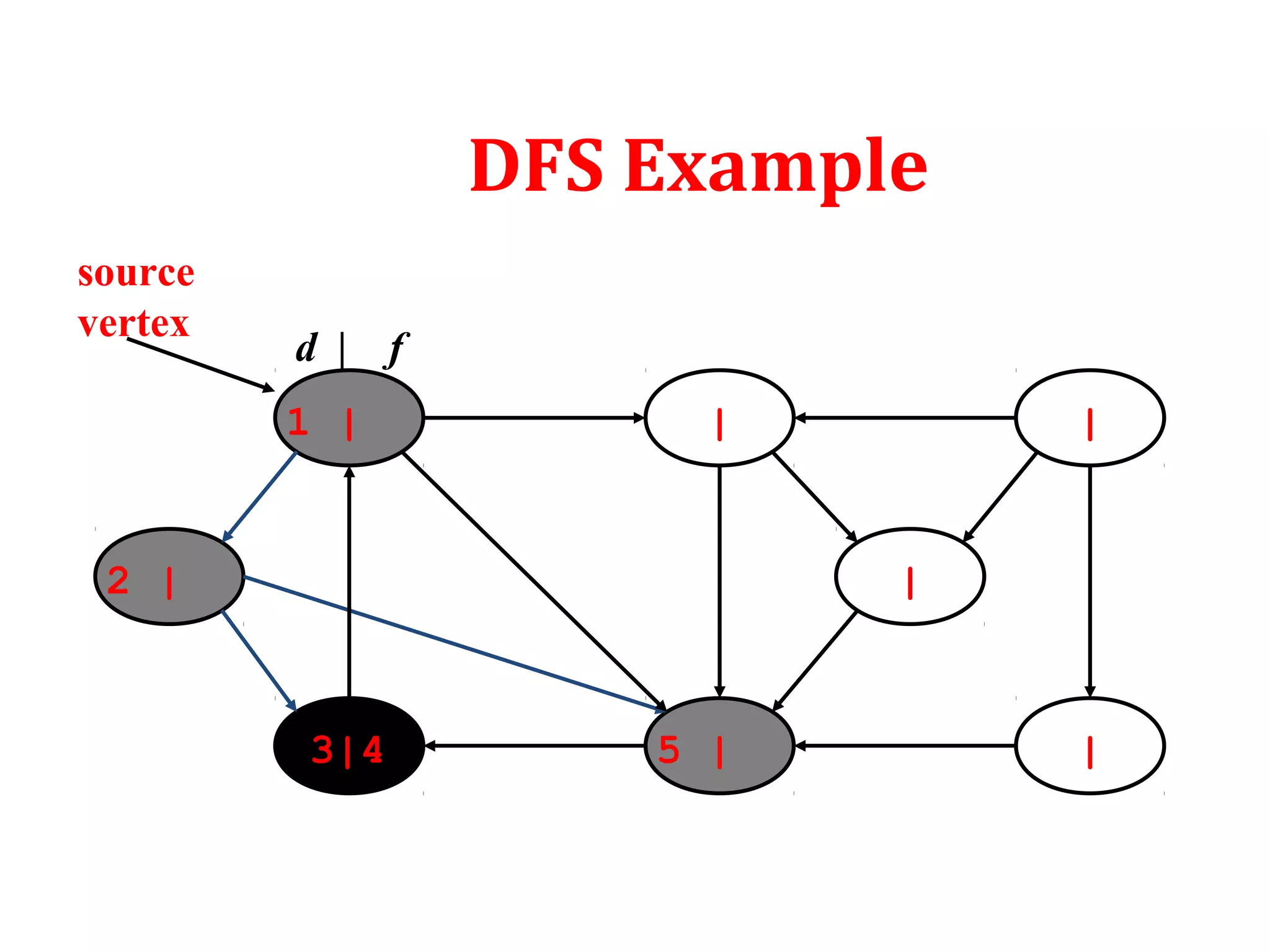
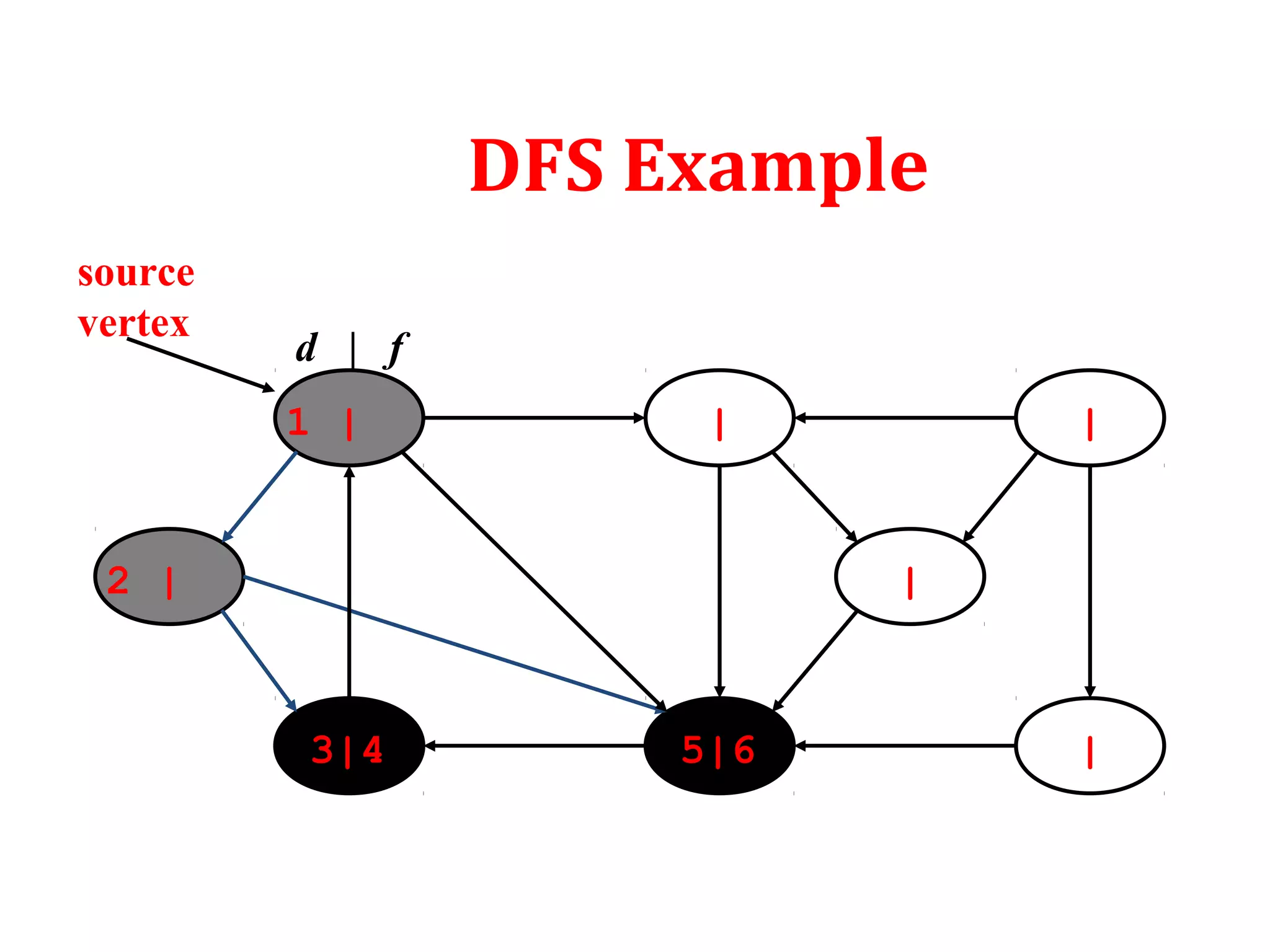
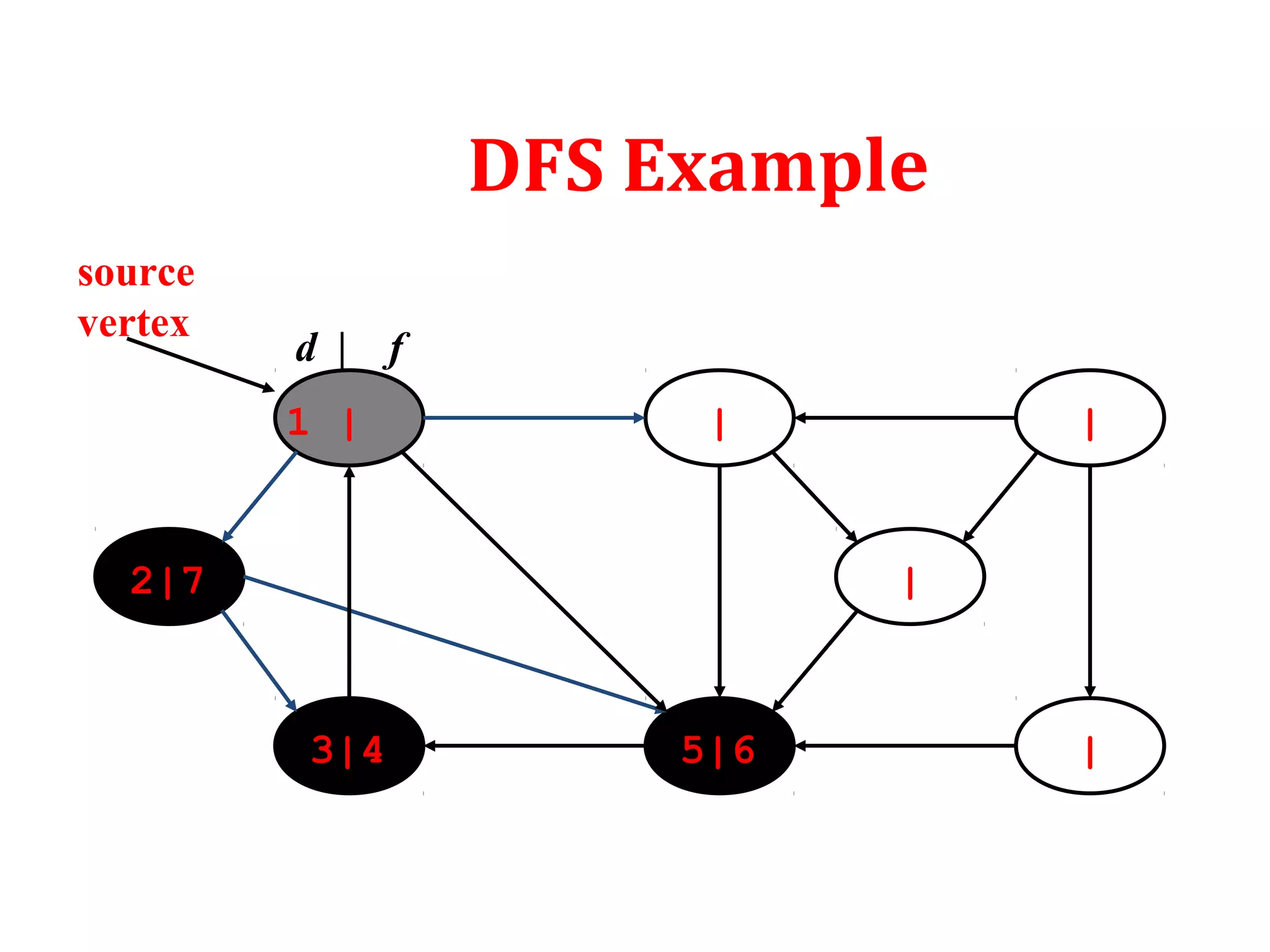
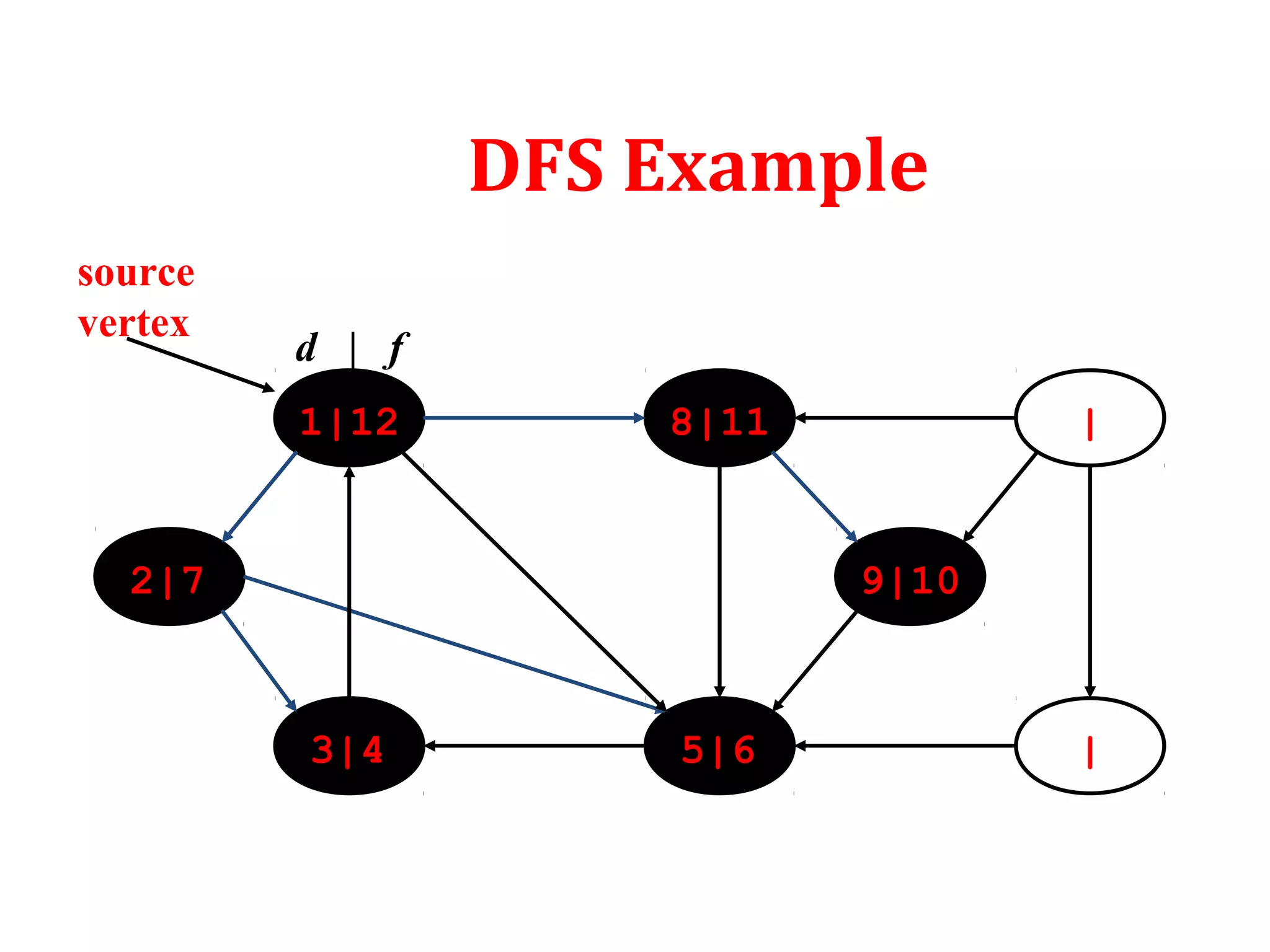
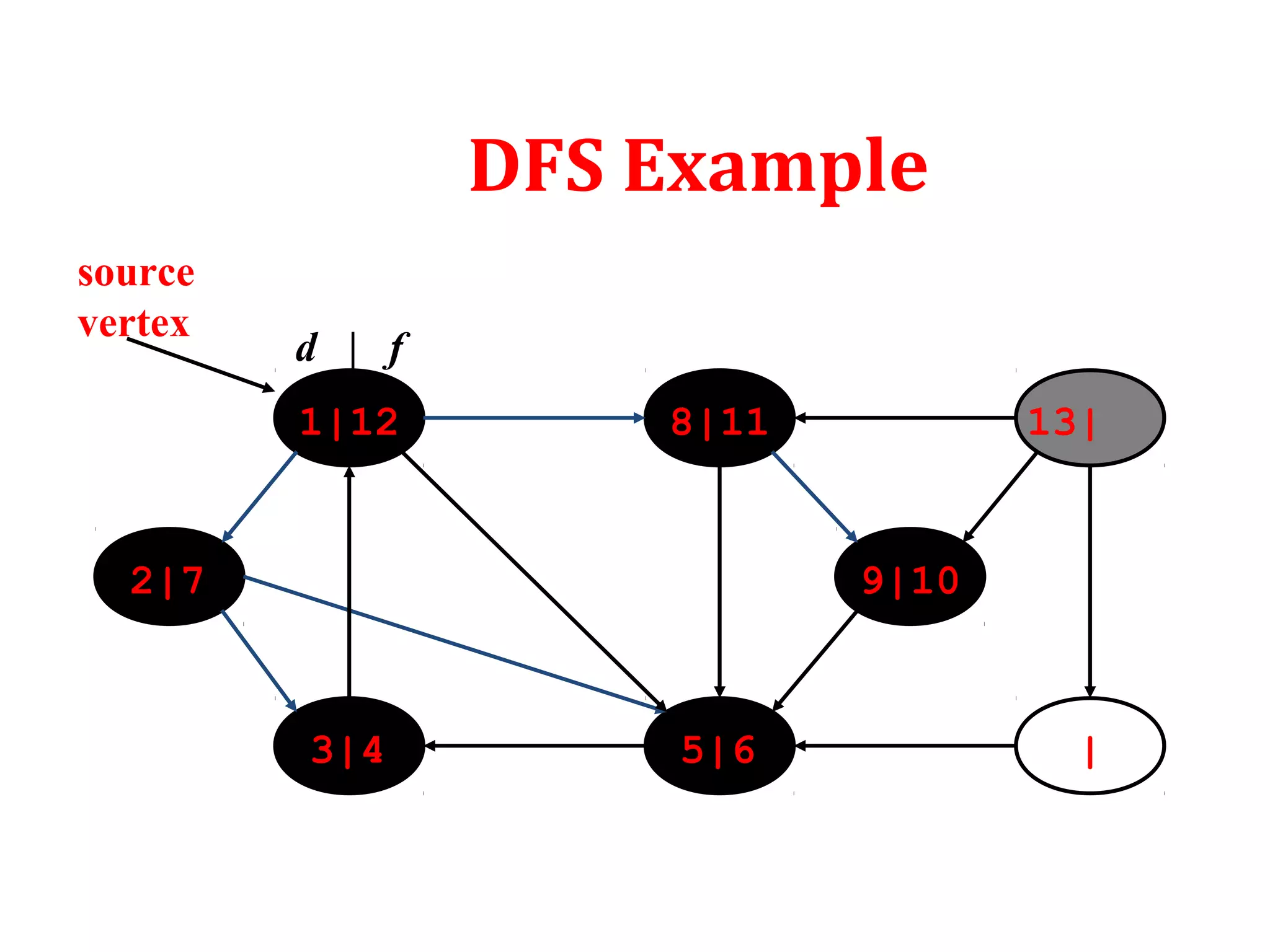
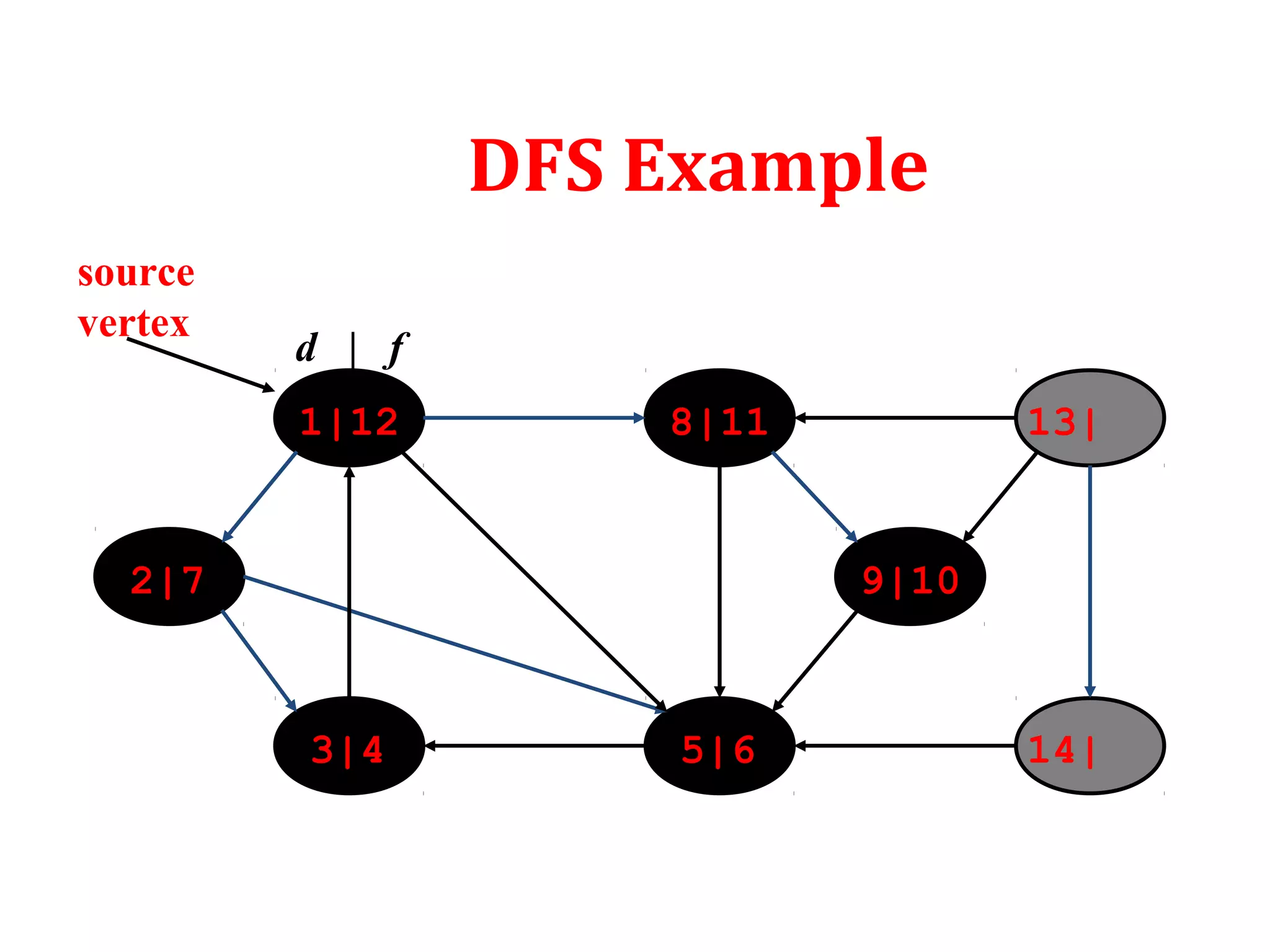
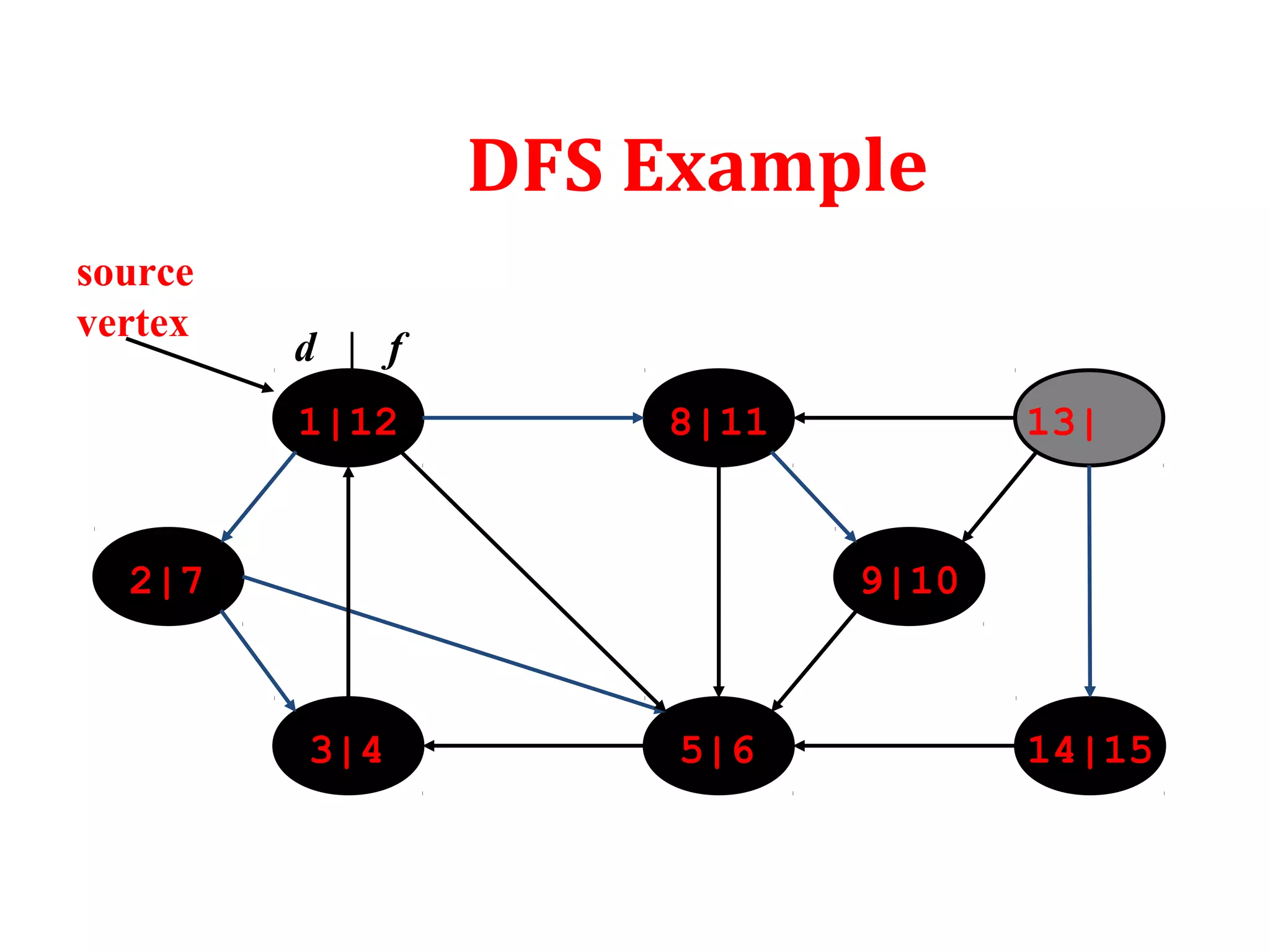
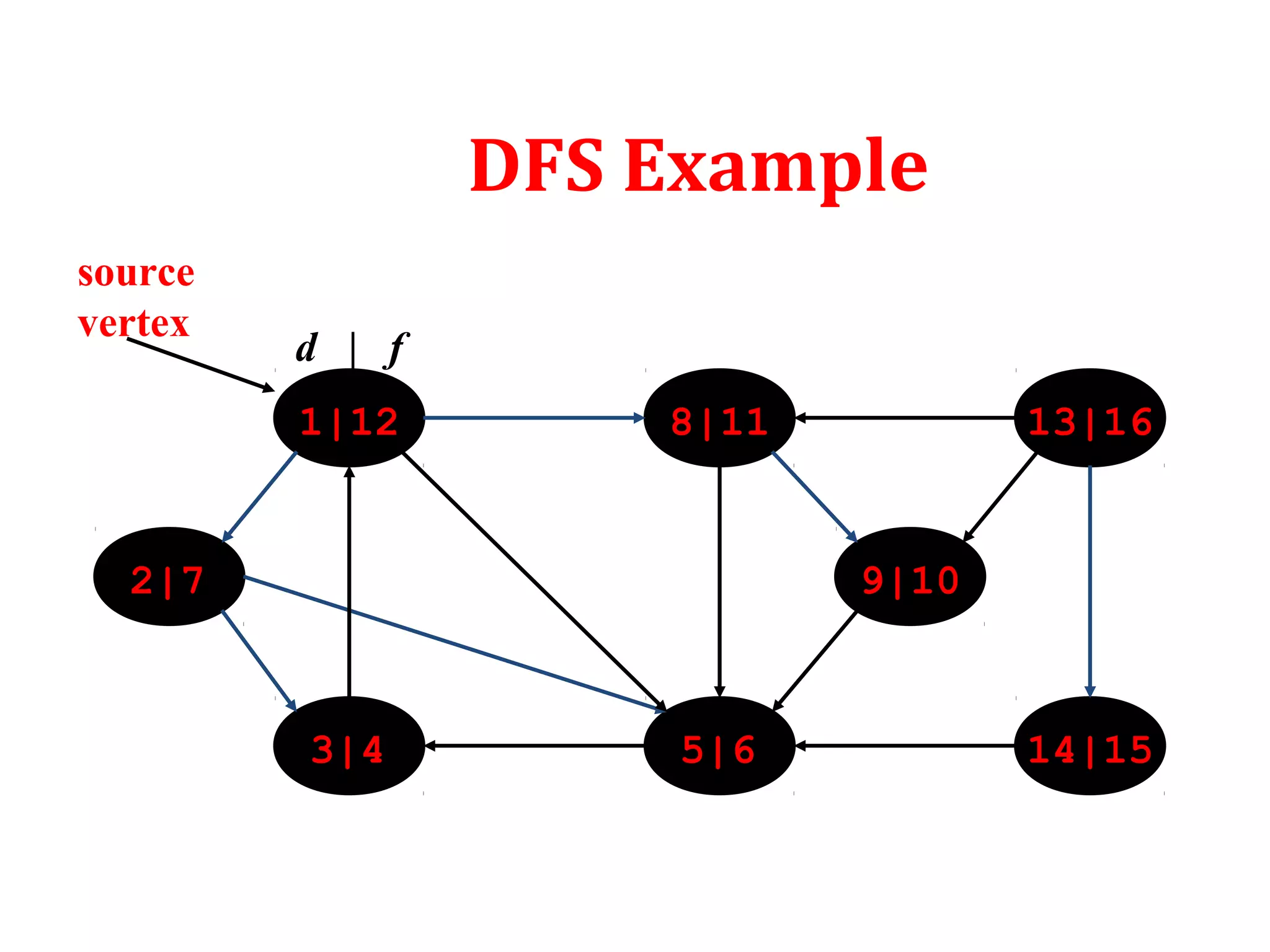
DFS: Algorithm (Cont.)
source
vertex

24. DFS Example
source
vertex

25. DFS Example
1 | | |
|||
| |
source
vertex
d | f

26. DFS Example
1 | | |
|||
2 | |
source
vertex
d | f

27. DFS Example
1 | | |
||3 |
2 | |
source
vertex
d | f

28. DFS Example
1 | | |
||3|4
2 | |
source
vertex
d | f

29. DFS Example
1 | | |
|5 |3|4
2 | |
source
vertex
d | f

30. DFS Example
1 | | |
|5|63|4
2 | |
source
vertex
d | f

31. DFS Example
1 | | |
|5|63|4
2|7 |
source
vertex
d | f

32. DFS Example
1 | 8 | |
|5|63|4
2|7 |
source
vertex
d | f

33. DFS Example
1 | 8 | |
|5|63|4
2|7 9 |
source
vertex
d | f

34. DFS Example
1 | 8 | |
|5|63|4
2|7 9|10
source
vertex
d | f

35. DFS Example
1 | 8|11 |
|5|63|4
2|7 9|10
source
vertex
d | f

36. DFS Example
1|12 8|11 |
|5|63|4
2|7 9|10
source
vertex
d | f

37. DFS Example
1|12 8|11 13|
|5|63|4
2|7 9|10
source
vertex
d | f

38. DFS Example
1|12 8|11 13|
14|5|63|4
2|7 9|10
source
vertex
d | f

39. DFS Example
1|12 8|11 13|
14|155|63|4
2|7 9|10
source
vertex
d | f

40. DFS Example
1|12 8|11 13|16
14|155|63|4
2|7 9|10
source
vertex
d | f

41. DFS: Complexity Analysis
 Initialization complexity is O(V)
 DFS_VISIT is called exactly once for each vertex
 And DFS_VISIT scans all the edges which causes
cost of O(E)
 Thus overall complexity is O(V + E)

42. DFS: Application
• Topological Sort
• Strongly Connected Component

43. Classification of Edges
 Another interesting property of DFS is that the DFS can be
used to classify the edges of the input graph G=(V,E). The DFS
creates depth first forest which can have four types of edges:
 Tree edge: Edge (u,v) is a tree edge if v was first discovered
by exploring edge (u,v). White color indicates tree edge.
 Back edge: Edge (u,v) is a back edge if it connects a vertex u
to a ancestor v in a depth first tree. Gray color indicates back
edge.
 Forward edge: Edge (u,v) is a forward edge if it is non-tree
edge and it connects a vertex u to a descendant v in a depth
first tree. Black color indicates forward edge.
 Cross edge: rest all other edges are called the cross edge.
Black color indicates forward edge.

44. Example of Edges

45. Theorem Derived from DFS
 Theorem 1: In a depth first search of an undirected
graph G, every edge of G is either a tree edge or
back edge.
 Theorem 2: A directed graph G is acyclic if and only
if a depth-first search of G yields no back edges.

46. Container of BFS and DFS
 Choice of container used to store discovered
vertices while graph search…
 If a queue is used as the container, we get
breadth first search.
 If a stack is used as the container, we get depth
first search.

47. Problem to Solve
Mawa
Dhaka
Majir
Ghat
Jajira
Shariat
pur
Naria
Bheder
Gong
University

48. MD. Shakhawat Hossain
Student of Computer Science & Engineering Dept.
University of Rajshahi