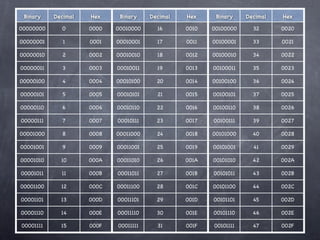
The document discusses different number bases: decimal, binary, and hexadecimal. It defines what each base means and lists their digits. For binary, it gives an example of adding two binary numbers by carrying digits to the next column like decimal. It also includes a table that lists binary, decimal, and hexadecimal numbers and their values.

1. Binary and Hexidecimal
Learning how to count in different bases

2. Decimal - Base 10
From the Latin, "decimus" meaning
"tenth"
Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

3. Binary - Base 2
From the Latin, "binarius" meaning
"consisting of two"
Digits: 0, 1

4. Hexadecimal - Base 16
In Greek, "hexa" means "six"
Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

5. Adding Binary
0001 0111
+ 0000 0011
Any time you add 1+1, then you carry
the result into the next column like you
would if you reached 10 in decimal.

6. Adding Binary
1
0001 0111
+ 0000 0011
0

7. Adding Binary
1
0001 0111
+ 0000 0011
10

8. Adding Binary
1
0001 0111
+ 0000 0011
010

9. Adding Binary
0001 0111
+ 0000 0011
1010

10. Adding Binary
0001 0111
+ 0000 0011
1 1010

11. Adding Binary
0001 0111
+ 0000 0011
0001 1010

12. Binary Decimal Hex Binary Decimal Hex Binary Decimal Hex
00000000 0 0000 00010000 16 0010 00100000 32 0020
00000001 1 0001 00010001 17 0011 00100001 33 0021
00000010 2 0002 00010010 18 0012 00100010 34 0022
00000011 3 0003 00010011 19 0013 00100011 35 0023
00000100 4 0004 00010100 20 0014 00100100 36 0024
00000101 5 0005 00010101 21 0015 00100101 37 0025
00000110 6 0006 00010110 22 0016 00100110 38 0026
00000111 7 0007 00010111 23 0017 00100111 39 0027
00001000 8 0008 00011000 24 0018 00101000 40 0028
00001001 9 0009 00011001 25 0019 00101001 41 0029
00001010 10 000A 00011010 26 001A 00101010 42 002A
00001011 11 000B 00011011 27 001B 00101011 43 002B
00001100 12 000C 00011100 28 001C 00101100 44 002C
00001101 13 000D 00011101 29 001D 00101101 45 002D
00001110 14 000E 00011110 30 001E 00101110 46 002E
00001111 15 000F 00011111 31 001F 00101111 47 002F