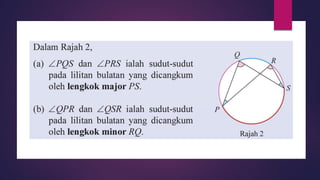
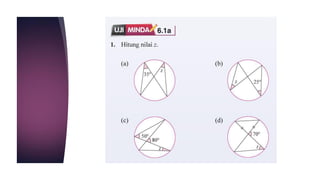
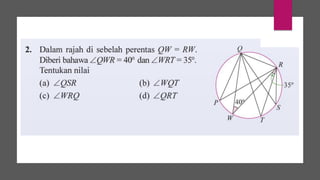
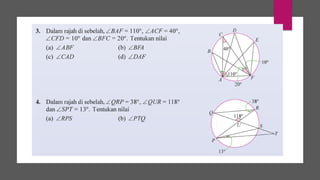
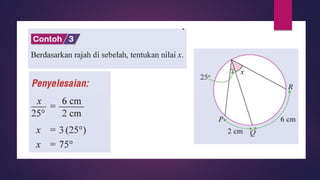
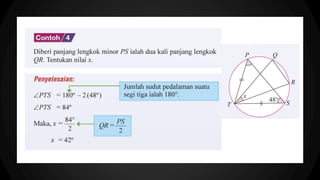
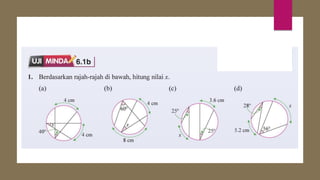
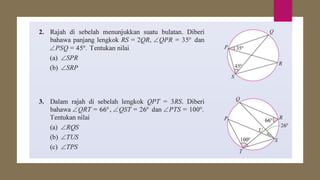
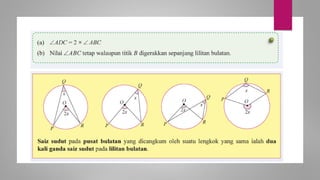
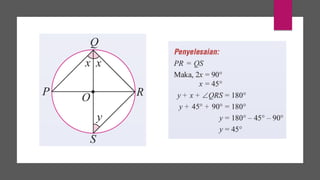
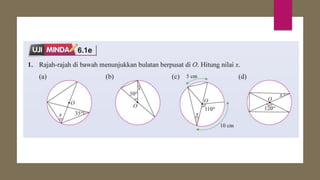
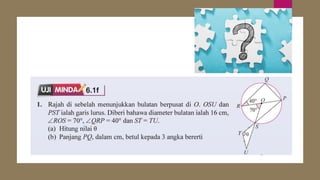
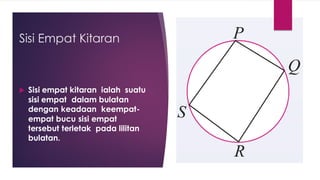
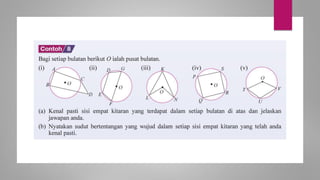
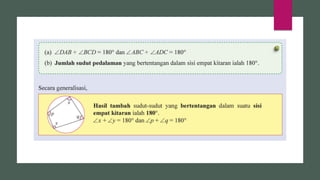
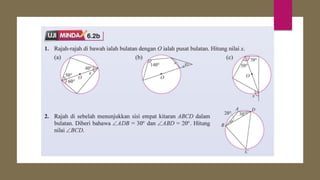
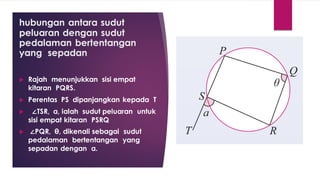
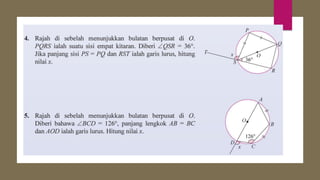
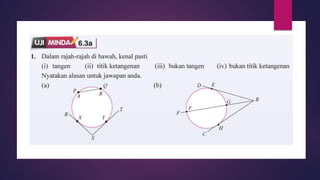
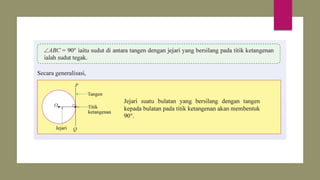
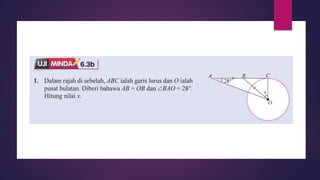
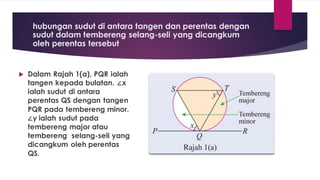
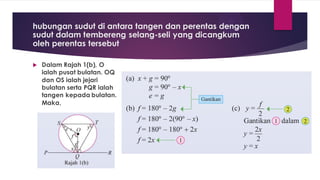
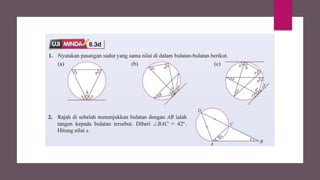
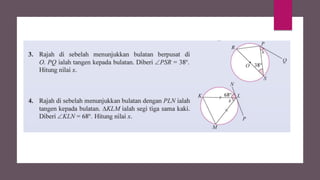
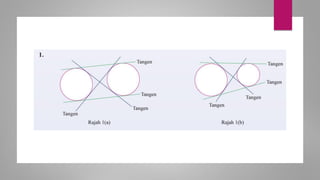
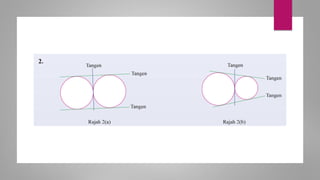
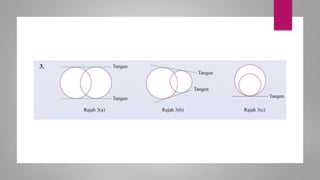
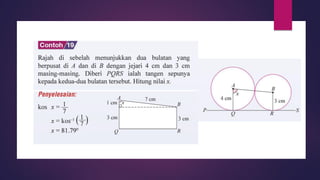
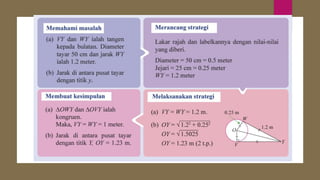
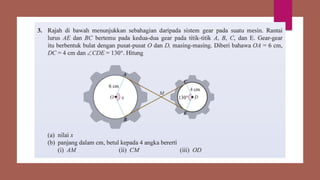
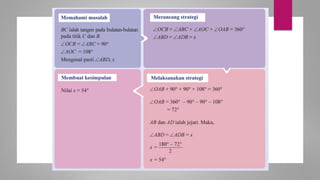
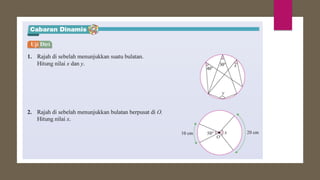
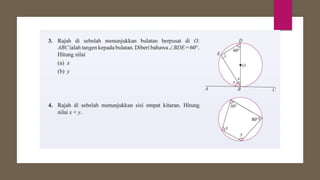
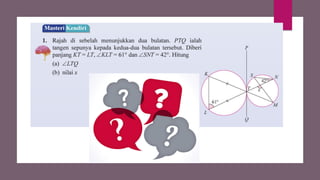
Dokumen ini membahas sudut dan tangen dalam bulatan untuk tingkatan 3 KSSM. Ia menerangkan ciri-ciri sudut pada lilitan, sudut pusat, serta sisi empat kitaran dalam bulatan, termasuk hubungan antara sudut pelurusan dan sudut pedalaman. Selain itu, dokumen ini juga mendedahkan konsep tangen kepada bulatan dan aplikasinya dalam situasi harian.