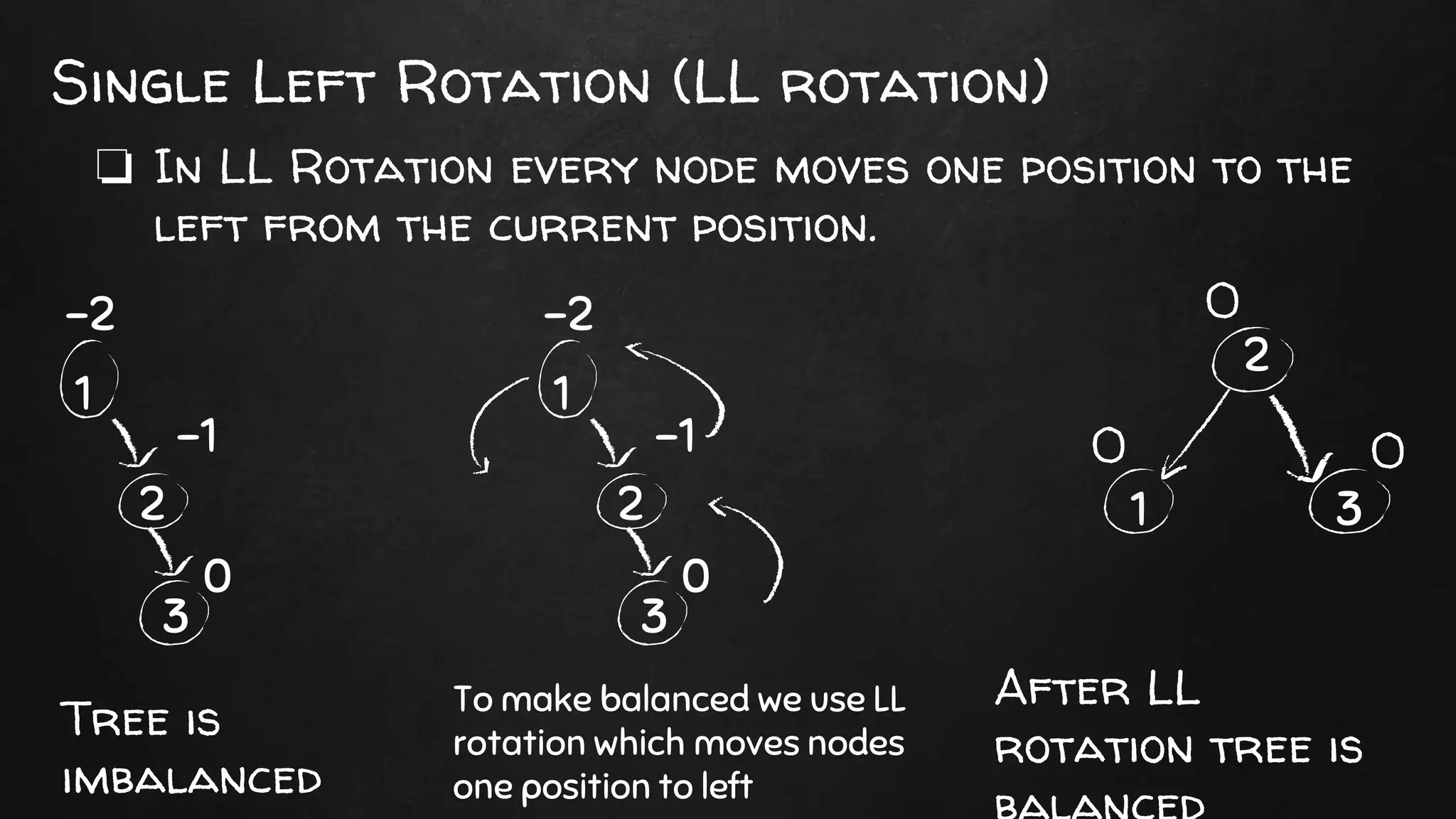
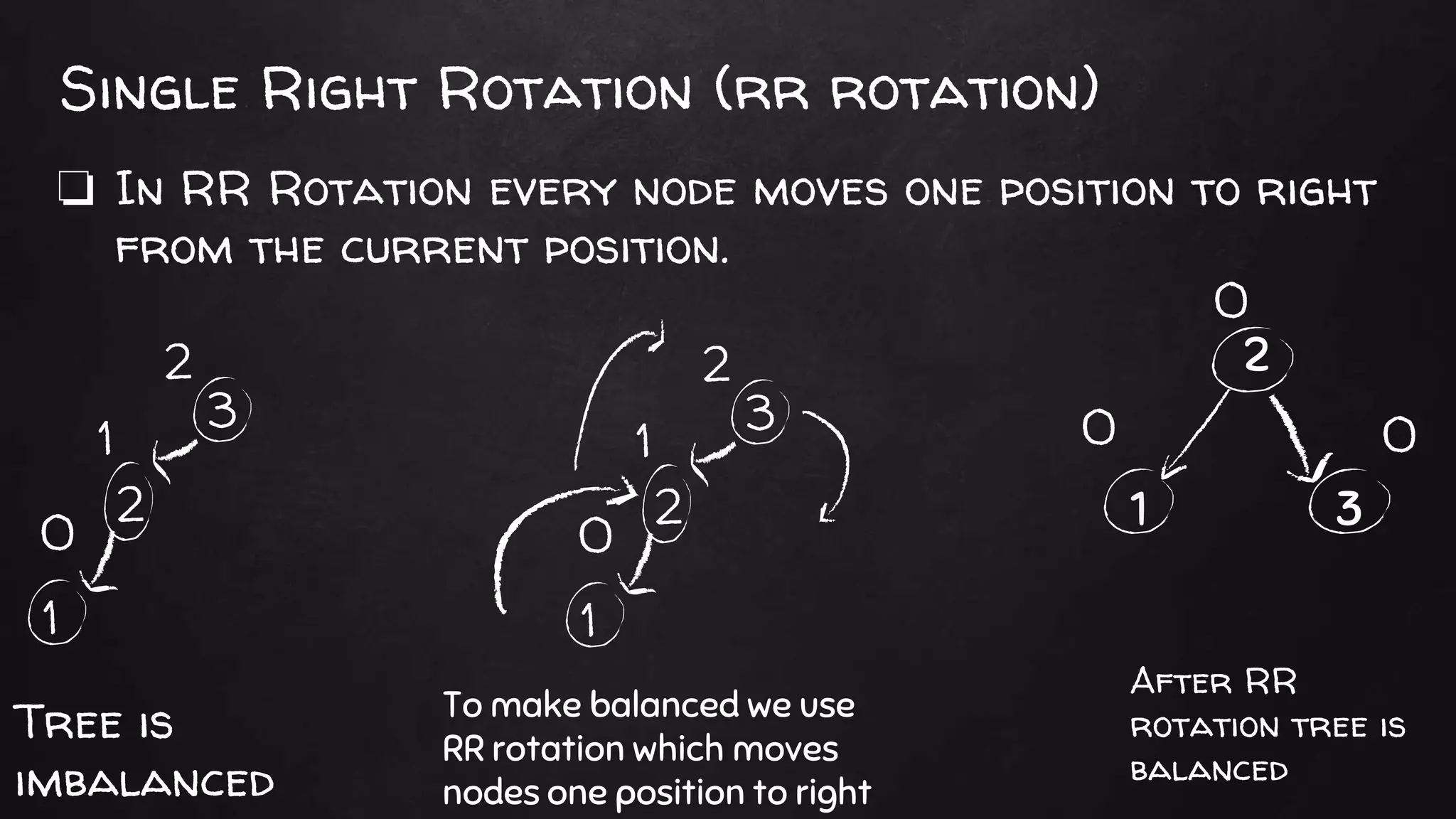
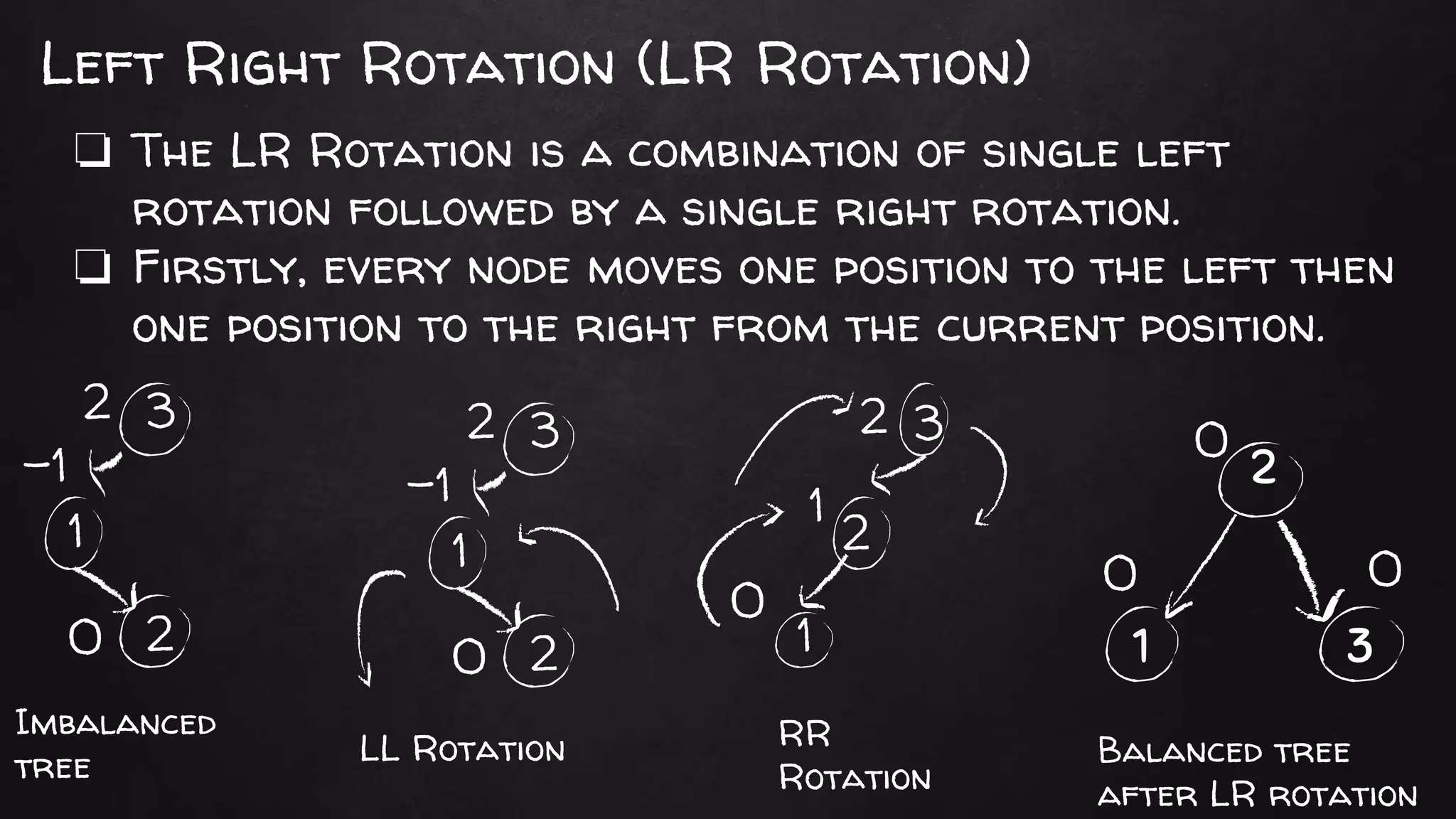
An AVL tree is a self-balancing binary search tree where the heights of the left and right subtrees of every node differ by at most one. Each node stores an extra "balance factor" field representing the height difference between its left and right subtrees. Rotations are performed during insertions and deletions to maintain the balance factor between -1 and 1, keeping the tree height balanced. There are four types of rotations - left, right, left-right, and right-left - to rebalance the tree as needed. Maintaining this balance property provides O(log n) time bounds for search, insert, and delete operations.

1. AVL TREE

2. Prerequisite knowledge
Binary tree
A tree in which each
node can at most have
2 descendents (child
nodes).
Binary Search Tree
A binary tree that has the
following properties -
1. All keys are unique.
2. Left key is always
smaller than right key.
3. The left and right
subtrees of the root are
also binary trees.
Height Balanced
Tree
A binary tree in which,
the longest path through
the left subtree is of the
same length as that of the
longest path from the
right subtree, from root to
leaf.

3. What An AVL TREE IS?
● An AVL tree is a self-balanced binary-search tree named
after its inventors Adelson-Velsky and Landis.
● A binary tree is said to be AVL balanced, if the difference
between the heights of the left and right subtrees of every
node in the tree is either -1,0 or +1.
● An extra information (balance factor) is maintained in
every node of an AVL tree.

4. Balance Factor
Balance_Factor =>
Height_of_left_Subtree - Height_of_right_subtree
Balance factor of a node is the difference between the heights of left and right
subtrees of that node.

5. A node N :
- with Balance_Factor (N) < 0 is called “left-heavy”
- with Balance_Factor (N) > 0 is called “right heavy”
- with Balance_Factor (N) = 0 is called “balanced”

6. AVL tree rotations
As the Balance_Factor change after every deletion or insertion, so, we
need to check for that. If there’s no change then we do conduct the
operation, otherwise, we make it balanced.
Rotation Operations are used to make a tree balanced. It is the process
of moving the nodes to either left or right to make the tree balanced.
There are four rotations of two types :
1. Single Rotations
a. Left Rotation (LL) b. Right
Rotation (RR)
1. Double Rotations

7. ❏ In LL Rotation every node moves one position to the
left from the current position.
Single Left Rotation (LL rotation)
1
-2
2
-1
3
0
2
31
1
-2
2
-1
3
0
Tree is
imbalanced
To make balanced we use LL
rotation which moves nodes
one position to left
After LL
rotation tree is
0
0 0

8. Single Right Rotation (rr rotation)
❏ In RR Rotation every node moves one position to right
from the current position.
2
31
After RR
rotation tree is
balanced
0
0 03
2
1
2
1
0
3
2
1
2
1
0
Tree is
imbalanced
To make balanced we use
RR rotation which moves
nodes one position to right

9. Left Right Rotation (LR Rotation)
❏ The LR Rotation is a combination of single left
rotation followed by a single right rotation.
❏ Firstly, every node moves one position to the left then
one position to the right from the current position.
3
1
2
2
-1
0
3
2
1
0
1
23
1
2
2
-1
0
2
31
0 0
0
Imbalanced
tree LL Rotation RR
Rotation
Balanced tree
after LR rotation

10. Right Left Rotation (RL rotation)
❏ The RL Rotation is a combination of single right
rotation followed by a single left rotation .
❏ Firstly, every node moves one position to the right then
one position to the left from the current position.
2
31
0 0
0
Balanced tree
after rL rotation
1
3
2 3
2
1-2
1
0
-2
-1
0
1
3
2
-2
1
0
Imbalanced
tree RR
Rotation
ll Rotation

11. AVL benefits
❏ Has an upper bound of O(log n) for
searching, insertion , deletion.
❏ To store data hierarchically.

12. Any questions?

13. Thank you
13