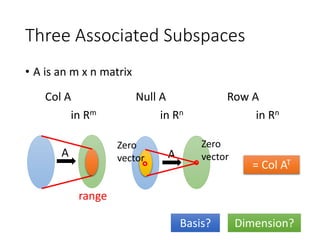
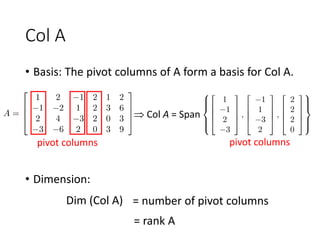
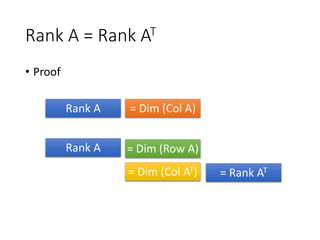
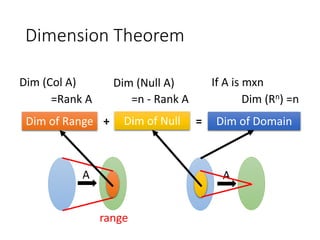
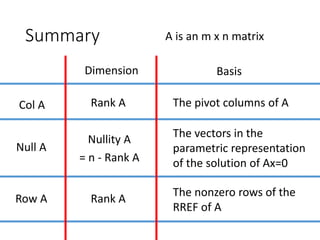
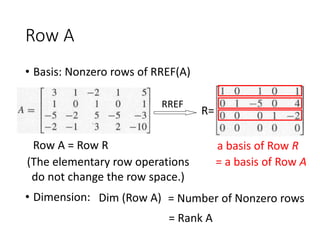
Col A: The pivot columns of A form the basis. The dimension is the rank of A. Null A: The free variables in the solution of Ax=0 form the basis. The dimension is the nullity of A. Row A: The nonzero rows of the RREF of A form the basis. The dimension is the rank of A.

1. Subspaces associated
with a Matrix
Hung-yi Lee

2. Reference
• Textbook: Chapter 4.3

3. Three Associated Subspaces
• A is an m x n matrix
Basis? Dimension?
Col A Null A Row A
in Rm in Rn in Rn
= Col AT
A
A
Zero
vector
range
Zero
vector

4. Col A
• Basis: The pivot columns of A form a basis for Col A.
• Dimension:
 Col A = Span
pivot columns pivot columns
Dim (Col A) = number of pivot columns
= rank A

5. Rank A (revisit)
Maximum number of Independent Columns
Number of Pivot Columns
Number of Non-zero rows
Number of Basic Variables
Dim (Col A): dimension of column space
Dimension of the range of A

6. Null A
• Basis:
• Solving Ax = 0
• Each free variable in the parametric representation of
the general solution is multiplied by a vector.
• The vectors form the basis.
𝐴 =
3
1
−5
−2
1
0
−2
−1
−2
1
5
3
1
0
−5
2
5
1
−3
−10
𝑅 =
1
0
0
0
0
1
0
0
1
−5
0
0
0
0
1
0
1
4
−2
0
𝑥1 + 𝑥3 + 𝑥5 = 0
𝑥2 − 5𝑥3 + 4𝑥5 = 0
𝑥4 − 2𝑥5 = 0
𝑥1 = −𝑥3 − 𝑥5
𝑥2 = 5𝑥3 − 4𝑥5
𝑥4 = 2𝑥5
𝑥1
𝑥2
𝑥3
𝑥4
𝑥5
= 𝑥3
−1
5
1
0
0
+ 𝑥5
−1
−4
0
2
1
𝑥3 = 𝑥3
𝑥5 = 𝑥5
Example 2, P256
Basis
(free)
(free)

7. Null A
• Basis:
• Solving Ax = 0
• Each free variable in the parametric representation of
the general solution is multiplied by a vector.
• The vectors form the basis.
• Dimension:
Dim (Null A) = number of free variables
= Nullity A
= n - Rank A

8. Row A
• Basis: Nonzero rows of RREF(A)
• Dimension:
RREF
a basis of Row R
R=
Row A = Row R
(The elementary row operations
do not change the row space.)
= a basis of Row A
Dim (Row A) = Number of Nonzero rows
= Rank A

9. Rank A (revisit)
Maximum number of Independent Columns
Number of Pivot Column
Number of Non-zero rows
Number of Basic Variables
Dim (Col A): dimension of column space
Dimension of the range of A
= Dim (Row A)
= Dim (Col AT)

10. Rank A = Rank AT
• Proof
= Dim (Row A)
= Dim (Col AT)
Rank A
Rank A = Dim (Col A)
= Rank AT

11. Dimension Theorem
Dim of Range Dim of Null Dim of Domain
A
A
range
+ =
Dim (Col A) Dim (Null A) If A is mxn
=Rank A =n - Rank A Dim (Rn) =n

12. Summary
Col A
Null A
Row A
Rank A
Nullity A
Rank A
= n - Rank A
A is an m x n matrix
Dimension Basis
The pivot columns of A
The vectors in the
parametric representation
of the solution of Ax=0
The nonzero rows of the
RREF of A