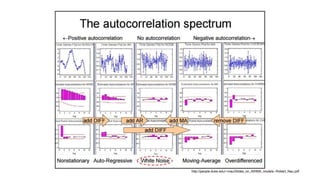
1. The optimal order of differencing for an ARIMA model is often the order that results in the lowest standard deviation of the differenced time series. 2. Changing the order of differencing changes the assumptions made about the time series - no differencing assumes stationarity, one difference assumes a random walk, and two differences assumes a time-varying trend. 3. The choice of AR and MA terms depends on whether the differenced time series has positive or negative autocorrelation at lag 1 - AR terms work best for positive autocorrelation and MA terms for negative autocorrelation. An MA term often fine-tunes a difference while an AR term compensates for the lack of a difference

1. Non seasonal arima

2. How many differences do I need to take?
Some simple rules
1. If the series has positive autocorrelations out to a high number of lags (say, 10 or more), then it
probably needs a higher order of differencing.
2. If the lag-1 autocorrelation is zero or negative, or the autocorrelations are all small and patternless,
then the series does not need a higher order of differencing. If the lag-1 autocorrelation is -0.5 or
more negative, the series may be overdifferenced. BEWARE OF OVERDIFFERENCING.
3. The optimal order of differencing is often the order of differencing at which the standard deviation
is lowest.

3. Do models change if I change the order of
differentiation?
Knowing what to expect
1. Model equivalence
a) A model with no orders of differencing assumes that the original series is stationary (among
other things, mean-reverting).
b) A model with one order of differencing assumes that the original series has a constant
average trend (e.g. a random walk or SES-type model, with or without growth).
c) A model with two orders of total differencing assumes that the original series has a time-
varying trend (e.g. a random trend or LES-type model).
2. Constant term
a. A model with no orders of differencing normally includes a constant term (which allows for a
non-zero mean value).
b. In a model with one order of total differencing, a constant term should be included if the series
has a non-zero average trend.
c. A model with two orders of total differencing normally does not include a constant term.

4. Model equivalence, continued
• ARIMA(p,d,q) forecasting equation
ARIMA(1,0,0) = first-order autoregressive model
ARIMA(0,1,0) = random walk
ARIMA(1,1,0) = differenced first-order autoregressive model
ARIMA(0,1,1) without constant = simple exponential smoothing
ARIMA(0,1,1) with constant = simple exponential smoothing with
growth
ARIMA(0,2,1) or (0,2,2) without constant = linear exponential
smoothing
ARIMA(1,1,2) with constant = damped-trend linear exponential
smoothing

5. http://people.duke.edu/~rnau/Slides_on_ARIMA_models--Robert_Nau.pdf

6. Do you need both AR and MA terms?
In general, you don’t. Rough rules of thumb:
• If the stationarized series has positive autocorrelation at lag 1, AR terms often work best.
• If it has negative autocorrelation at lag 1, MA terms often work best.
An MA(1) term often works well to fine-tune the effect of a nonseasonal difference, while an AR(1)
term often works well to compensate for the lack of a nonseasonal difference, so the choice between
them may depend on whether a difference has been used.