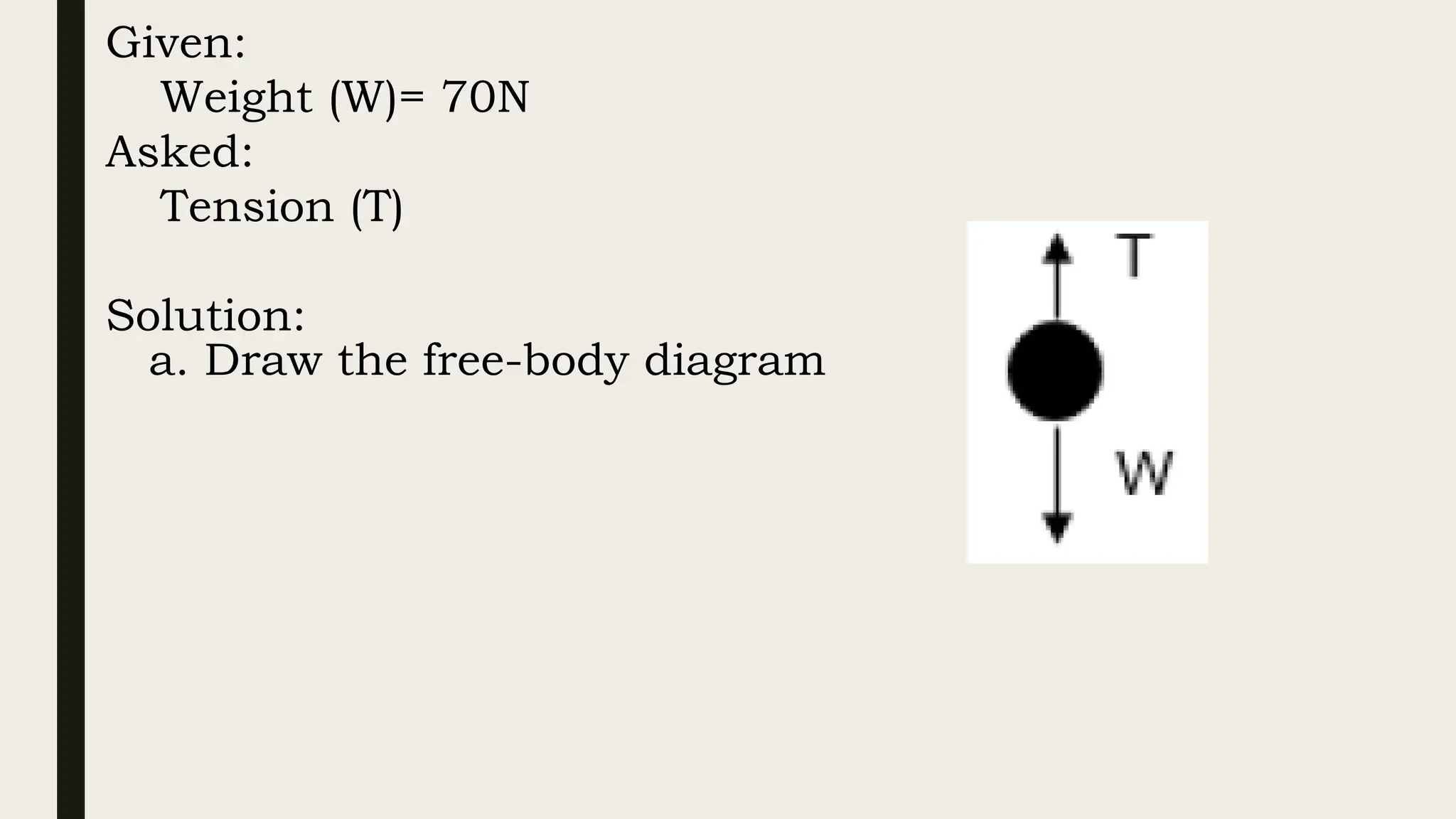
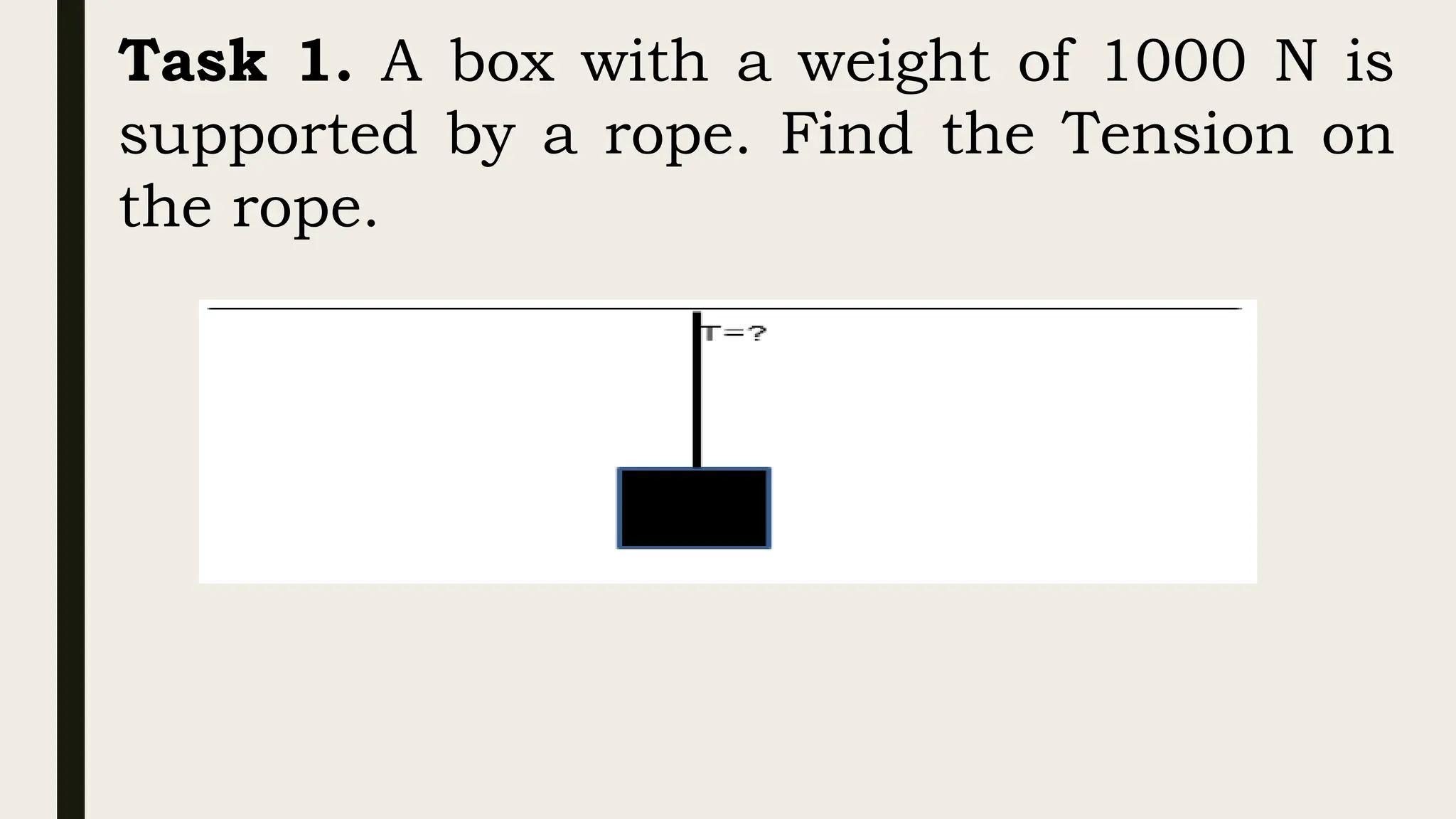
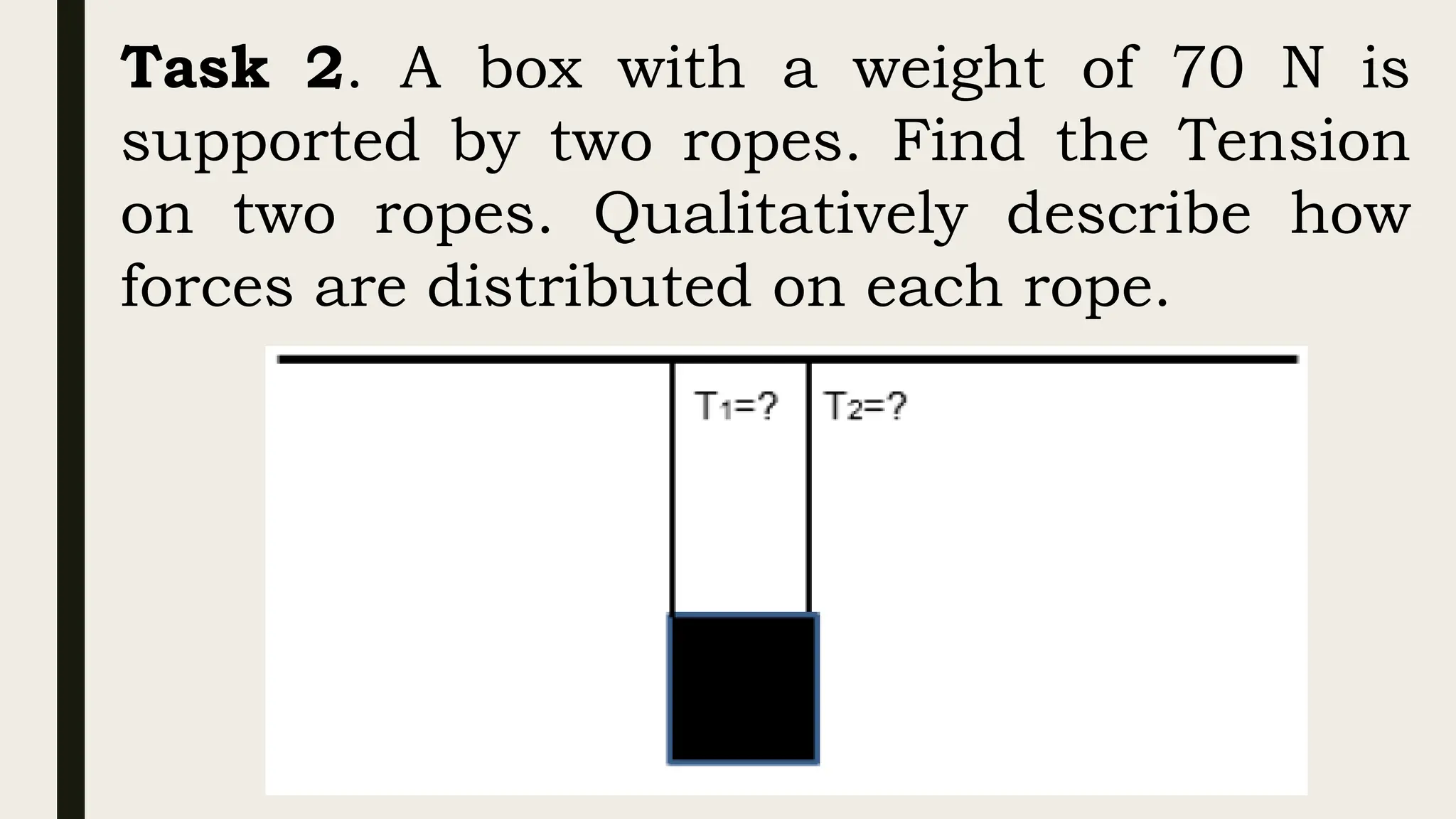
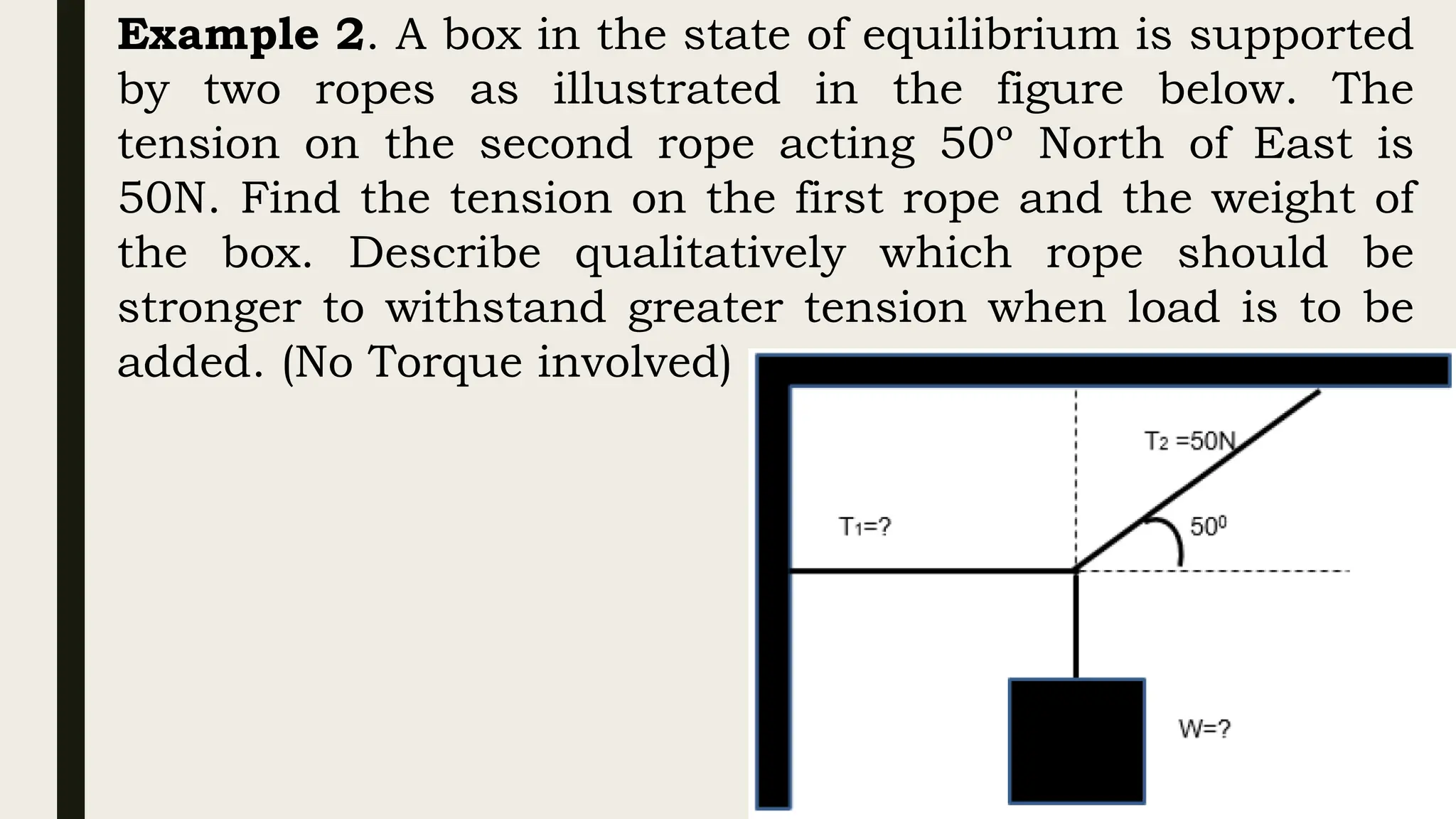
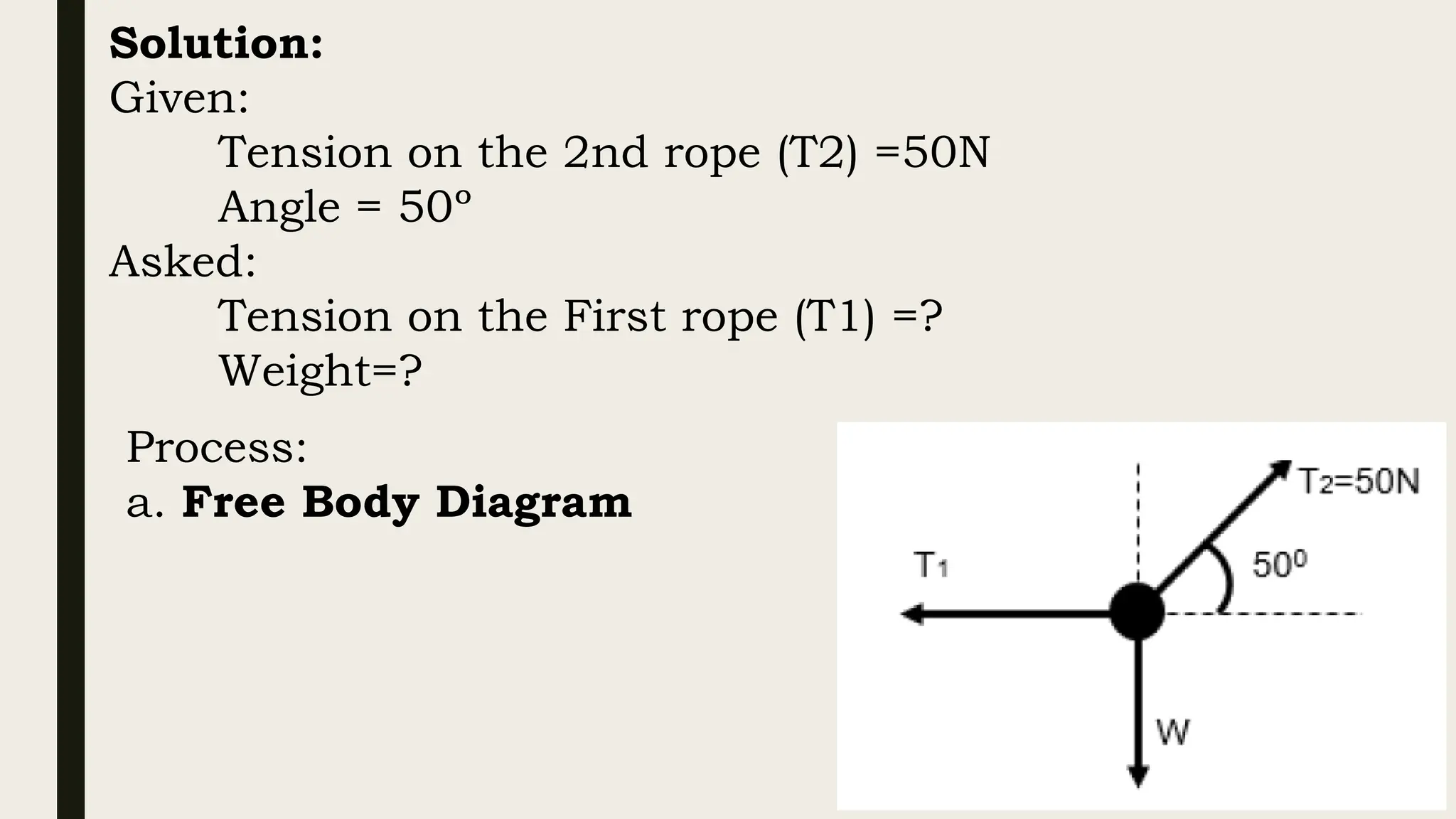
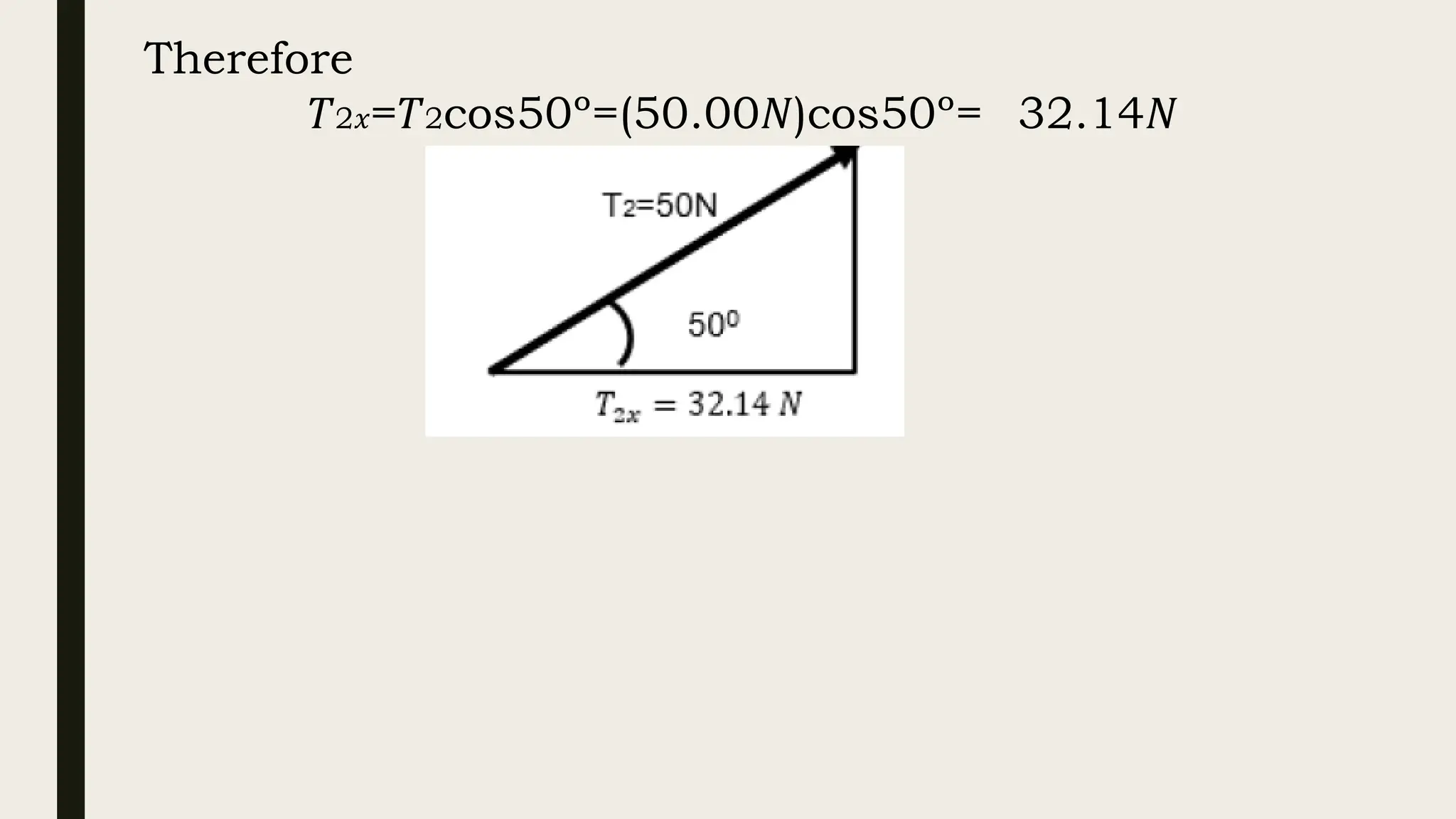
The document discusses the application of Newton's laws of motion, particularly regarding forces in equilibrium and friction. It classifies forces into contact (e.g., static and kinetic friction) and non-contact forces, explaining equilibrium conditions where the sum of forces and torques acting on an object equals zero. Various examples demonstrate problem-solving techniques for calculating tension in supporting ropes and the weights of boxes in equilibrium.

1. APPLICATION OF NEWTON’S
LAW OF MOTION ON FORCES
ACTING ON BODIES AT
EQUILIBRIUM AND FRICTION

2. Some problems in physics deal with
concurrent forces; such forces have a line
of action that converges at a particular
point.
Like forces acting on the object of interest
in a free-body diagram, all external forces
pass at the object as a point.

3. Forces can be categorized as contact and
noncontact forces.
A push, pull, tension, compression, friction,
and the normal force are examples of
contact forces since you can establish a
physical contact point between the applied
force and the object.

4. Noncontact forces on the other hand, are
forces generated at a distance from the
object. The electromagnetic forces and the
weight are examples of this type of force.

5. According to Newton’s First Law of
motion, when there is no net force, object
at rest will remain at rest while object
moving at a constant speed will continue
to move constantly.

6. You can therefore infer that stationary
object or those moving in constant speed
are acted upon by several forces that
cancel each other or by no force at all.
On this condition the object is said to be
on the state of equilibrium.

7. The object is in the state of equilibrium if it
satisfies two main conditions:
1. The summation of forces along certain axis
is zero.
This implies that forces acting along x-axis, y-
axis, and z-axis must be equal to zero. A
negative sign is attached to vectors that are
due west or those that are acting towards left.

8. The object is in the state of equilibrium if it
satisfies two main conditions:
The same negative sign is attached to vectors
that are moving due south or downward. The
positive value is given to those vectors acting
upward (north) and those acting east (right).
Σ𝑭=𝟎 Σ𝑭𝒙=𝟎 Σ𝑭𝒚=𝟎 and Σ𝑭𝒛=𝟎

9. The object is in the state of equilibrium if it
satisfies two main conditions:
2. The summation of torque acting on
an object is equal to zero.
Torque are forces that may cause object
to rotate at a particular axis.

10. The object is in the state of equilibrium if it
satisfies two main conditions:
The torque that tends to produce
clockwise rotation has a negative sign
while those that tend to produce
counterclockwise rotation is given a
positive sign.

11. Friction is a type of force that exists when
two surfaces are in contact or rub with
each other.
This type of force tends to reduce the
speed or motion of a moving object since it
always acts opposite to the direction of
object’s motion.
Friction

12. Friction
2 classification of Friction
1.Static Friction
This type of friction force is present when two
objects whose surfaces in contact are stationary
in relation to one another. Basically, this type
of force keeps stationary object on their resting
position.

13. Friction : 2 classifications
1.Static Friction
Static friction could be represented using
a symbol 𝑭𝒔, where F refers to the force
and the subscript s stands for static
friction.
Since friction is a type of force the unit
attached to this quantity is Newton (N).

14. Friction : 2 classifications
1.Static Friction
The magnitude of static friction could be
computed using the formula:
𝑭𝒔=𝝁𝒔 𝑭𝑵
Where 𝑭𝒔 refers to the static friction, 𝝁𝒔
refers to the coefficient of static friction,
and 𝑭𝑵 which refers to the normal force
acting on an object.

15. Friction : 2 classifications
1.Static Friction
Furthermore, this friction type tends to
oppose the initial or the start of a motion.
Static friction is dependent on the
magnitude of the force applied.
EXAMPLE: A book at rest on the top of a table.
Where the static friction acts in the absence of
relative motion between the two objects.

16. Friction : 2 classifications
2. Kinetic Friction
This type of friction force is present when
two objects whose surfaces are in contact
are moving in relation to one another.
Kinetic friction could be represented
using a symbol 𝑭𝒌 , where F refers to the
force and the subscript k stands for
kinetic friction.

17. Friction : 2 classifications
2. Kinetic Friction
The formula that could be used to
compute kinetic friction is: 𝑭𝒌=𝝁𝒌𝑭𝑵
Where 𝑭𝒌 refers to the kinetic friction, 𝝁𝒌
refers to the coefficient of kinetic friction
and 𝑭𝑵 refers to the normal force acting
on an object.

18. Friction : 2 classifications
2. Kinetic Friction
This type of friction acts as the object is in
motion relative to the other object in
contact. Kinetic friction is independent on
the magnitude of force applied.
EXAMPLE: A sack of cement sliding in an inclined
plane.
Where the kinetic friction acts relative to the motion of
two objects.

19. ACTIVITY 1.
Problem-Solving: Objects in Equilibrium Condition
Directions: Study the examples provided below and
apply the ideas learned to solve the various tasks
required. Write the answer on a separate sheet of
paper.

20. Given:
Weight (W)= 70N
Asked:
Tension (T)
Solution:
a. Draw the free-body diagram

21. b. Use the equilibrium condition
Σ𝑭𝒙=𝟎 & Σ𝑭𝒛=𝟎
(there are no forces identified acting along the x
& z-axis, there is also no torque that may cause
rotation)
Σ𝑭𝒚=𝟎 (Two forces are acting along the y-axis the
Tension and Weight)
Therefore:
Σ𝑭𝒚=𝟎; 𝑇−𝑊=0 (Tension is positive while
Weight is negative)

22. This results in 𝑇=𝑊; since,
W=70N
𝑇=70 𝑁
Qualitative Description:
The rope will experience a force equal to the
weight of the box.

23. Task 1. A box with a weight of 1000 N is
supported by a rope. Find the Tension on
the rope.

24. Task 2. A box with a weight of 70 N is
supported by two ropes. Find the Tension
on two ropes. Qualitatively describe how
forces are distributed on each rope.

25. Example 2. A box in the state of equilibrium is supported
by two ropes as illustrated in the figure below. The
tension on the second rope acting 50º North of East is
50N. Find the tension on the first rope and the weight of
the box. Describe qualitatively which rope should be
stronger to withstand greater tension when load is to be
added. (No Torque involved)

26. Solution:
Given:
Tension on the 2nd rope (T2) =50N
Angle = 50º
Asked:
Tension on the First rope (T1) =?
Weight=?
Process:
a. Free Body Diagram

27. b. Use the equilibrium condition
b1. Determining the tension on the first rope T1
Take note that Σ𝑭𝒙=𝟎 Summation of Forces along x- axis
should be equal to zero.
Forces along the x-axis are: T1 and T2x
T2x is the component of T2 along x –axis which could be
obtained using the formula
𝑇2𝑥 = 𝑇2cos𝜃

28. Therefore
𝑇2𝑥=𝑇2cos50º=(50.00𝑁)cos50º= 32.14𝑁

29. Considering that Σ𝑭𝒙=𝟎=(−𝑻𝟏+𝑻𝟐𝒙) You may notice that
T1 is negative since it is directed towards the left /west
direction, while 𝑇2𝑥 is positive since it is acting towards
the right/ east direction.
Solving for T1, the equation becomes:
(−𝑻𝟏+𝑻𝟐𝒙)=𝟎
𝒓𝒆𝒂𝒓𝒓𝒂𝒏𝒈𝒊𝒏𝒈 (𝑻𝟏)=𝑻𝟐𝒙 since 𝑇2𝑥=32.14 𝑁
therefore (𝑻𝟏)=𝟑𝟐.𝟏𝟒 𝑵

30. b2. Determining the Weight (W) of the box in
equilibrium state
Take note that Σ𝑭y=𝟎 Summation of Forces along y-axis
should be equal to zero.
Forces along the y-axis are: W and T2y
T2y is the component of T2 along y–axis which could be
obtained using the formula
𝑇2𝑦=𝑇2 sin 𝜃

31. Therefore 𝑇2𝑦 = 𝑇2sin50º= (50 𝑁)sin 50º= 38.30 𝑁
𝑇2𝑦 = 38.30 N
(−𝑾+𝑻𝟐𝒚)=𝟎
𝒓𝒆𝒂𝒓𝒓𝒂𝒏𝒈𝒊𝒏𝒈 𝑾= 𝑻𝟐𝒚 since 𝑇2𝑦= 38.30 𝑁
therefore 𝑾= 38.30 𝑵

32. c. Qualitative Description
The stronger rope should be used in rope number 2
since it will experience greater tension based on the
computation results where:
(𝑻𝟏)=𝟑𝟐.𝟏𝟒 𝑵 while T2=50N

33. TASK 3. A box in the state of equilibrium is supported
by two ropes as illustrated in the figure below. The
tension on the second rope acting 48º North of East is
90 N. Find the tension on the first rope and the weight
of the box. Describe qualitatively which rope should be
stronger to withstand greater tension when load is to
be added. (No Torque involved)