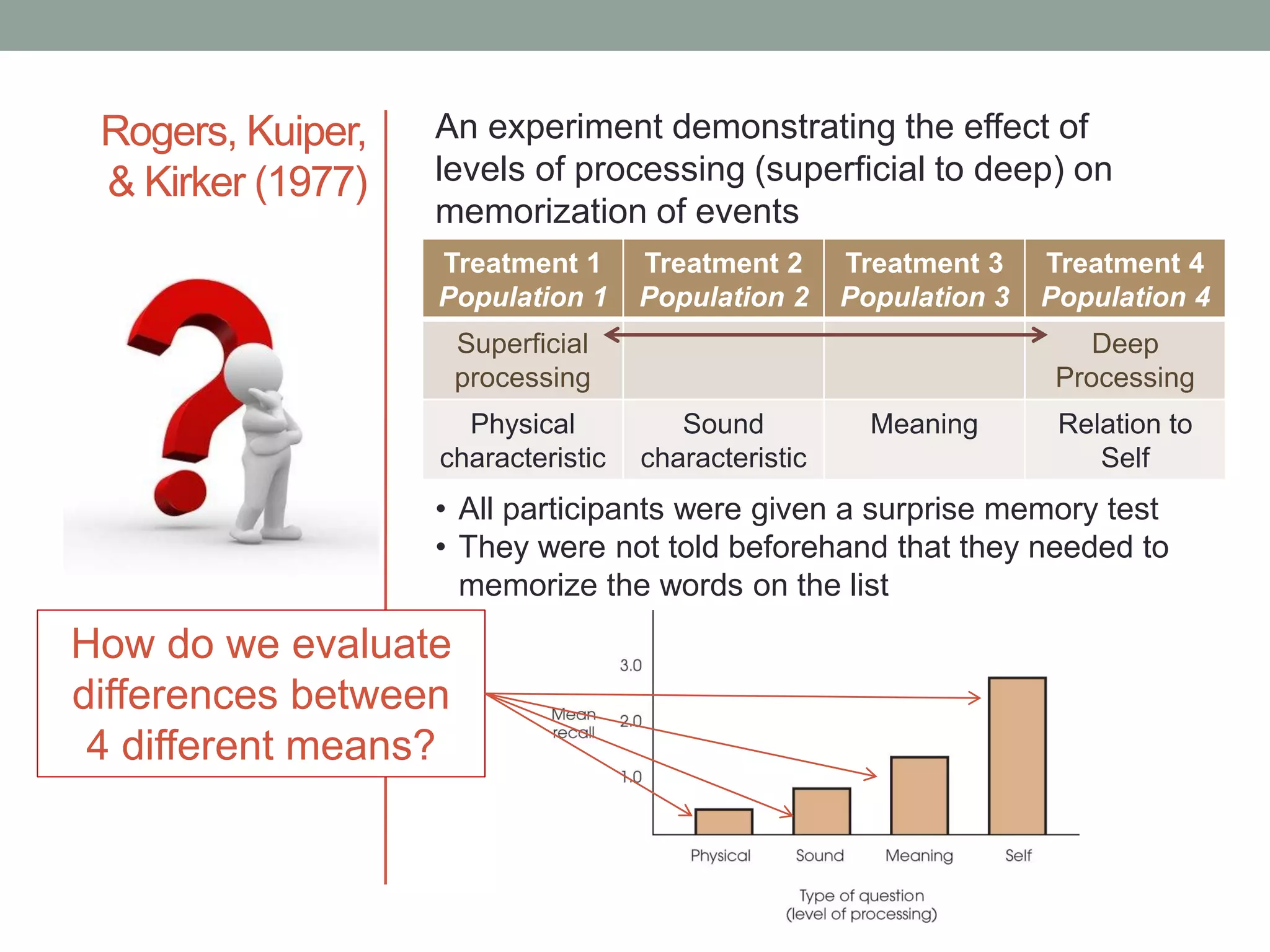
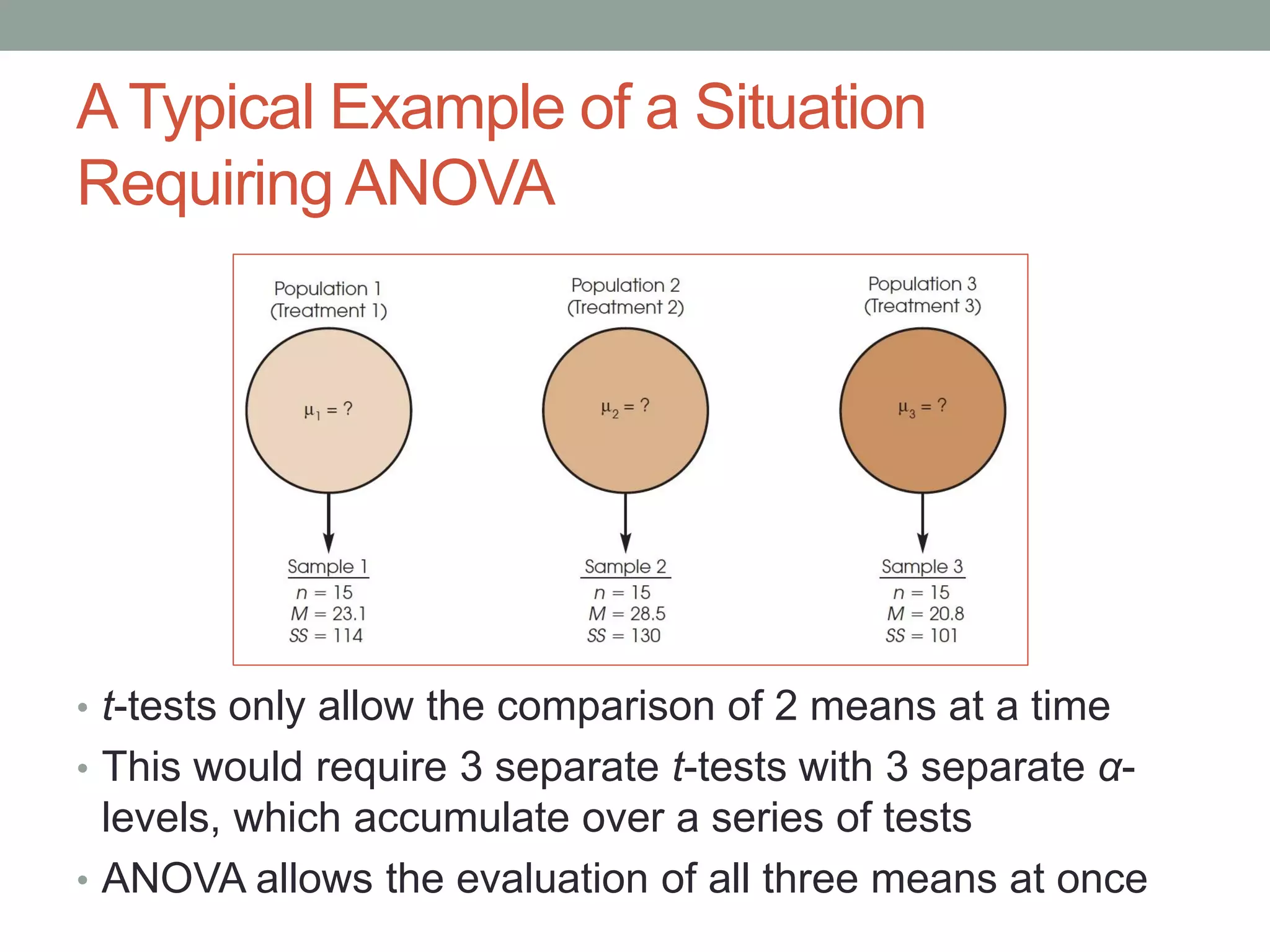
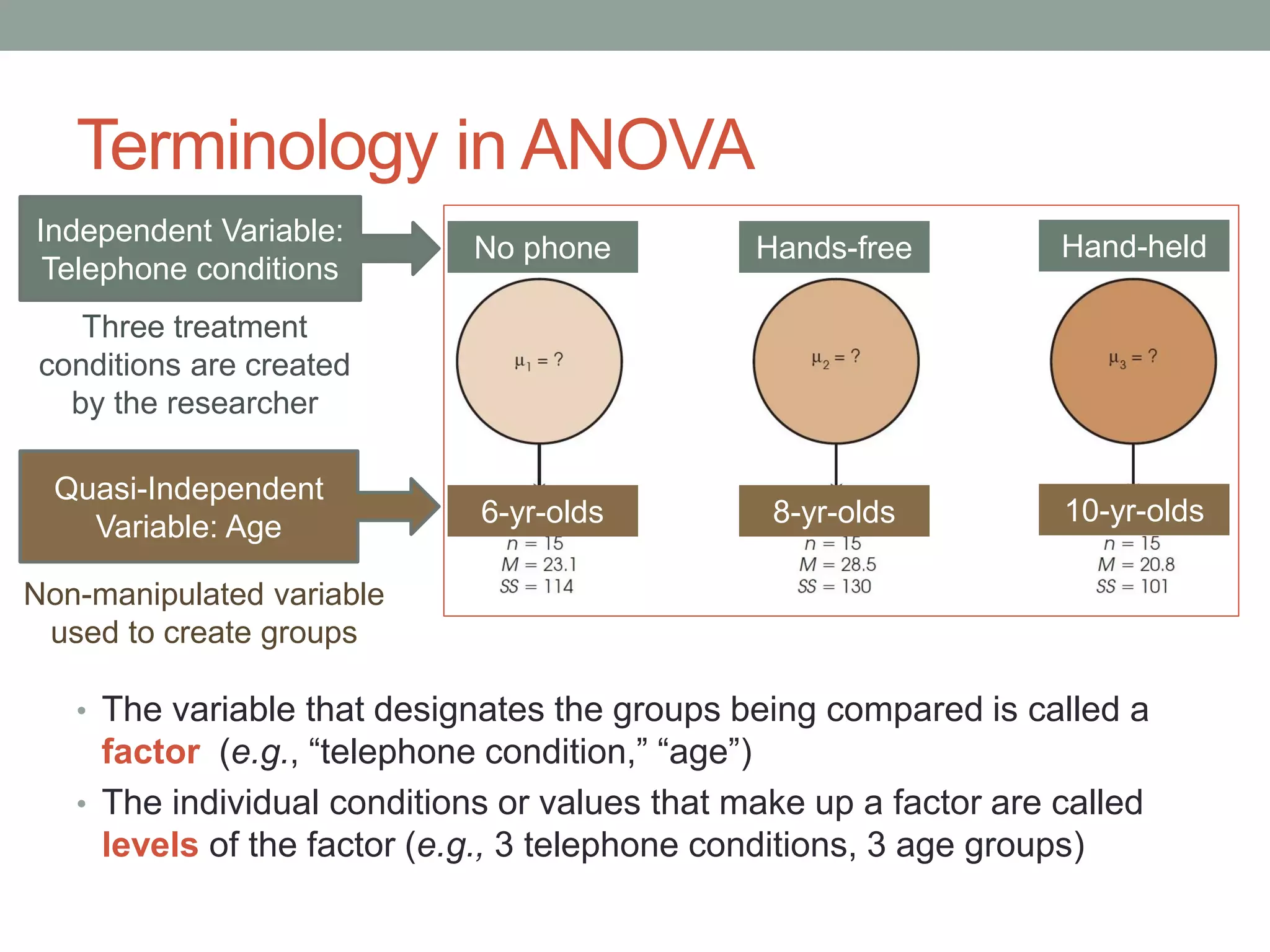
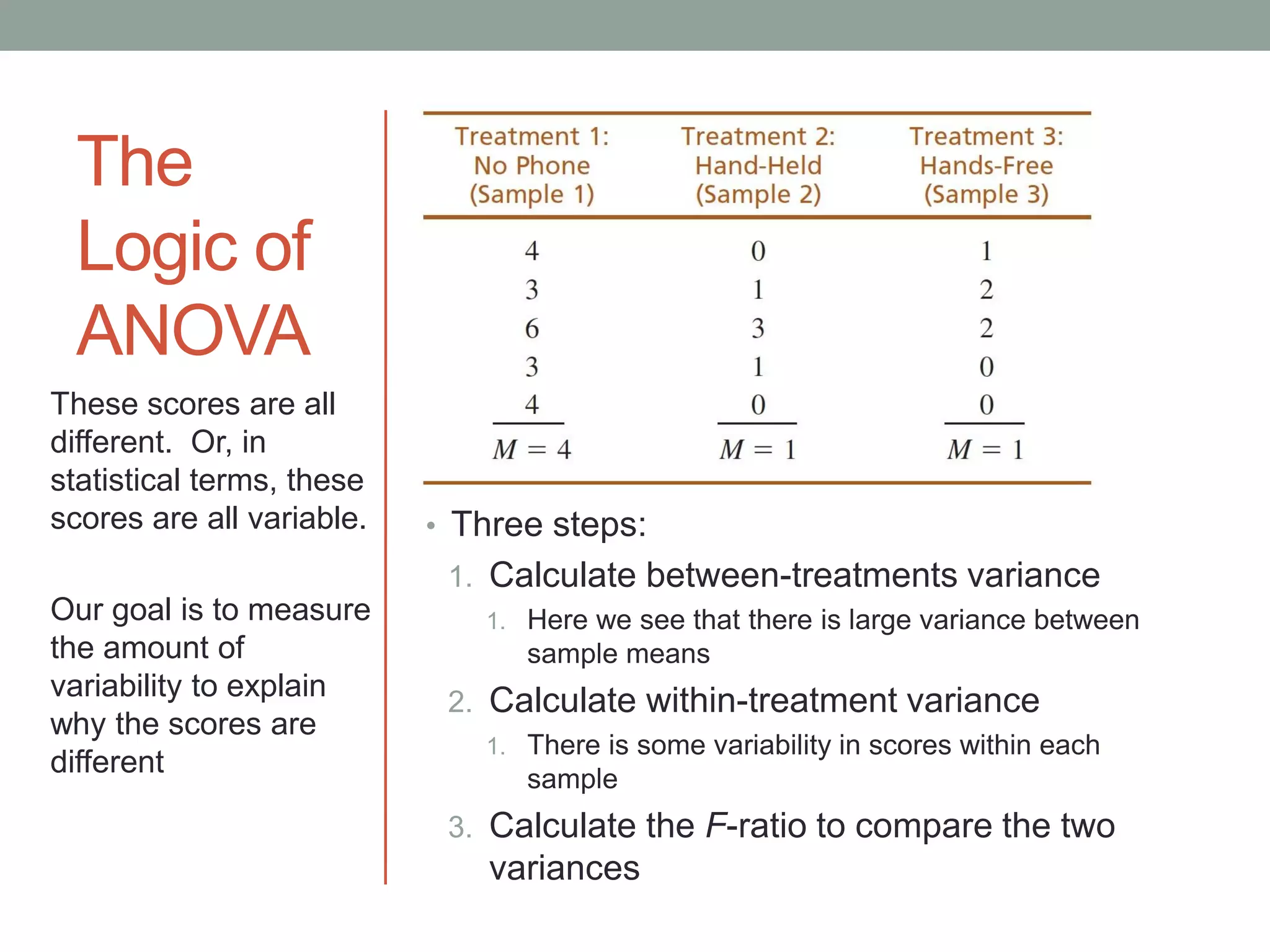
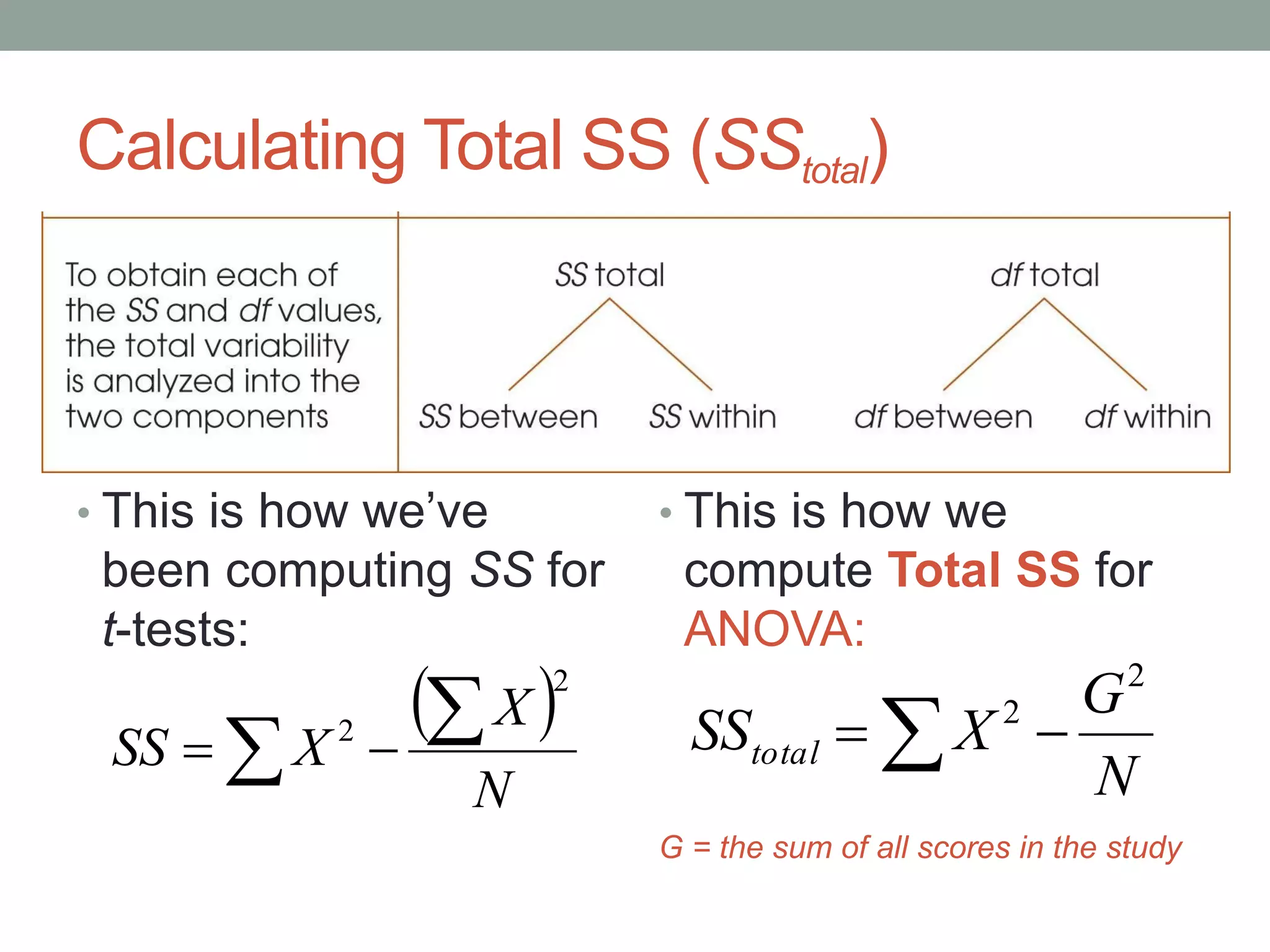
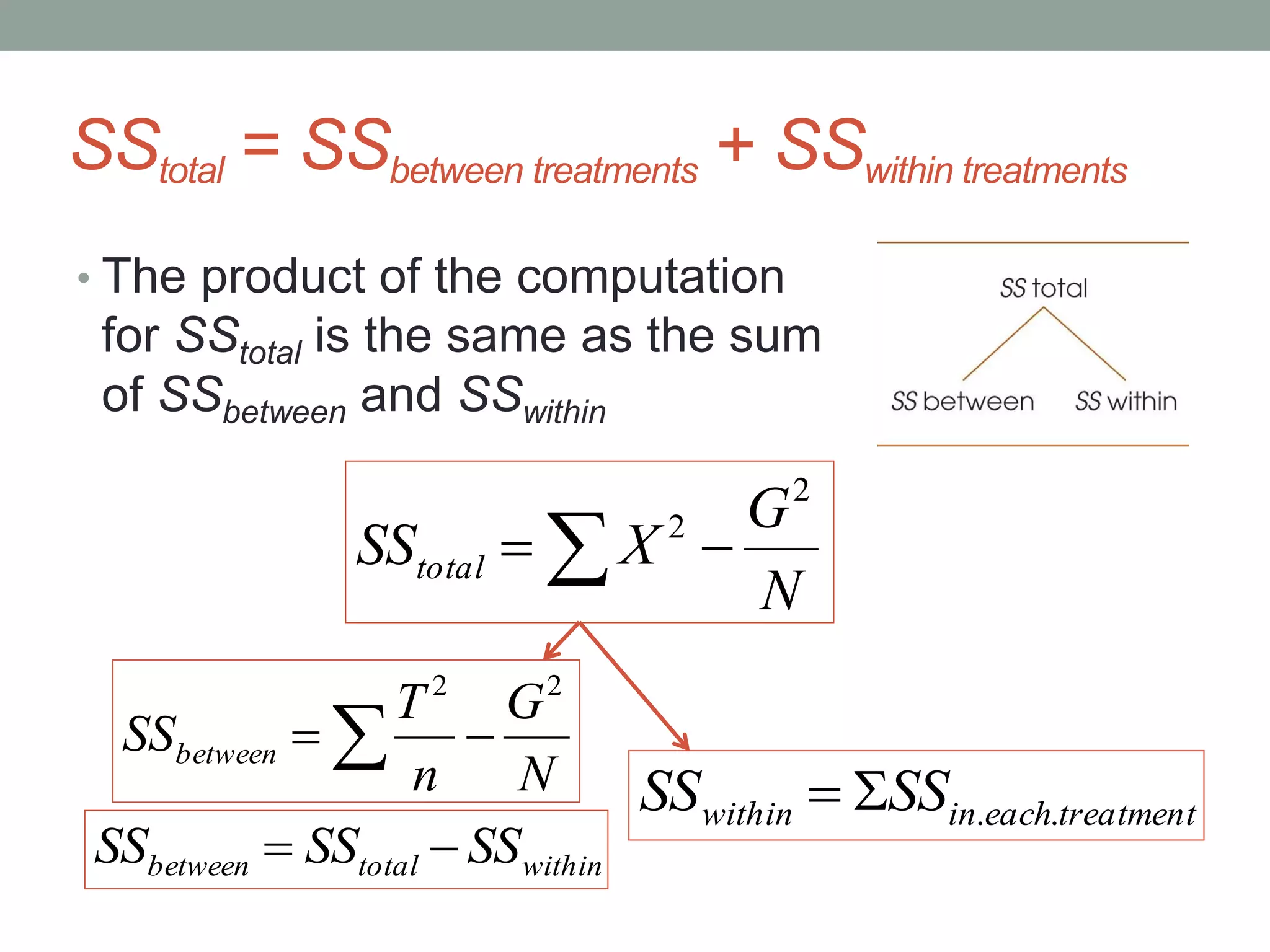
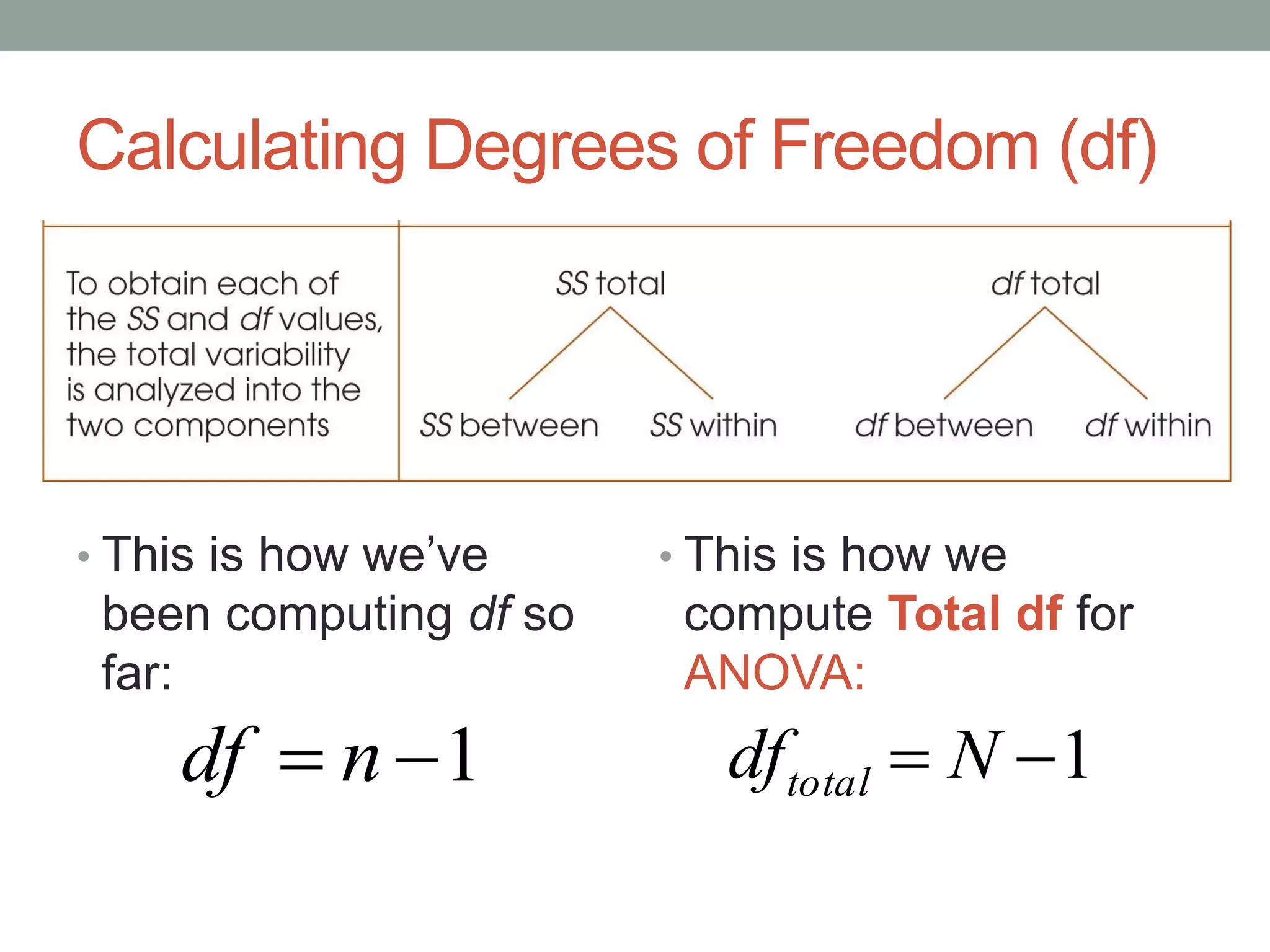
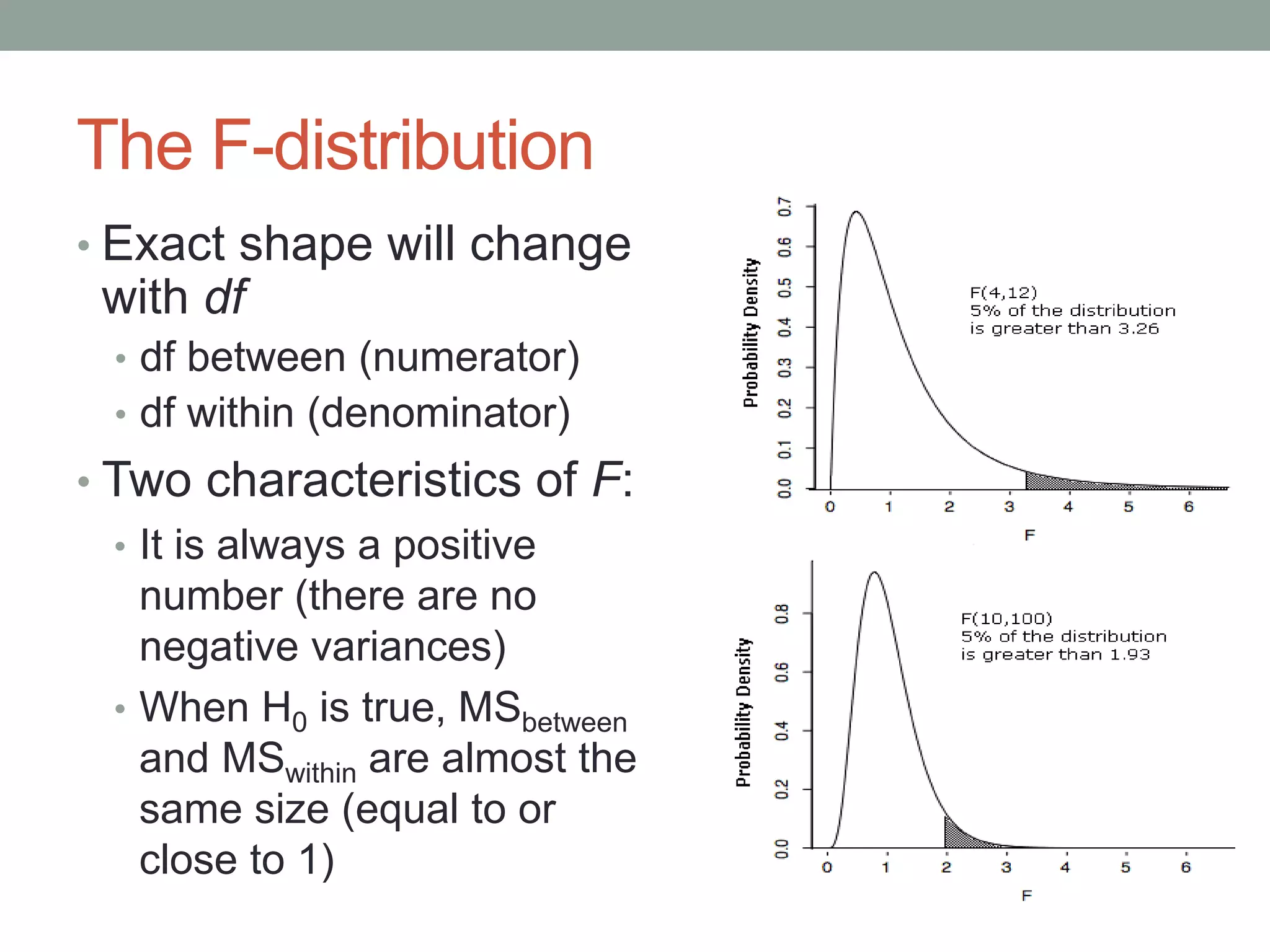
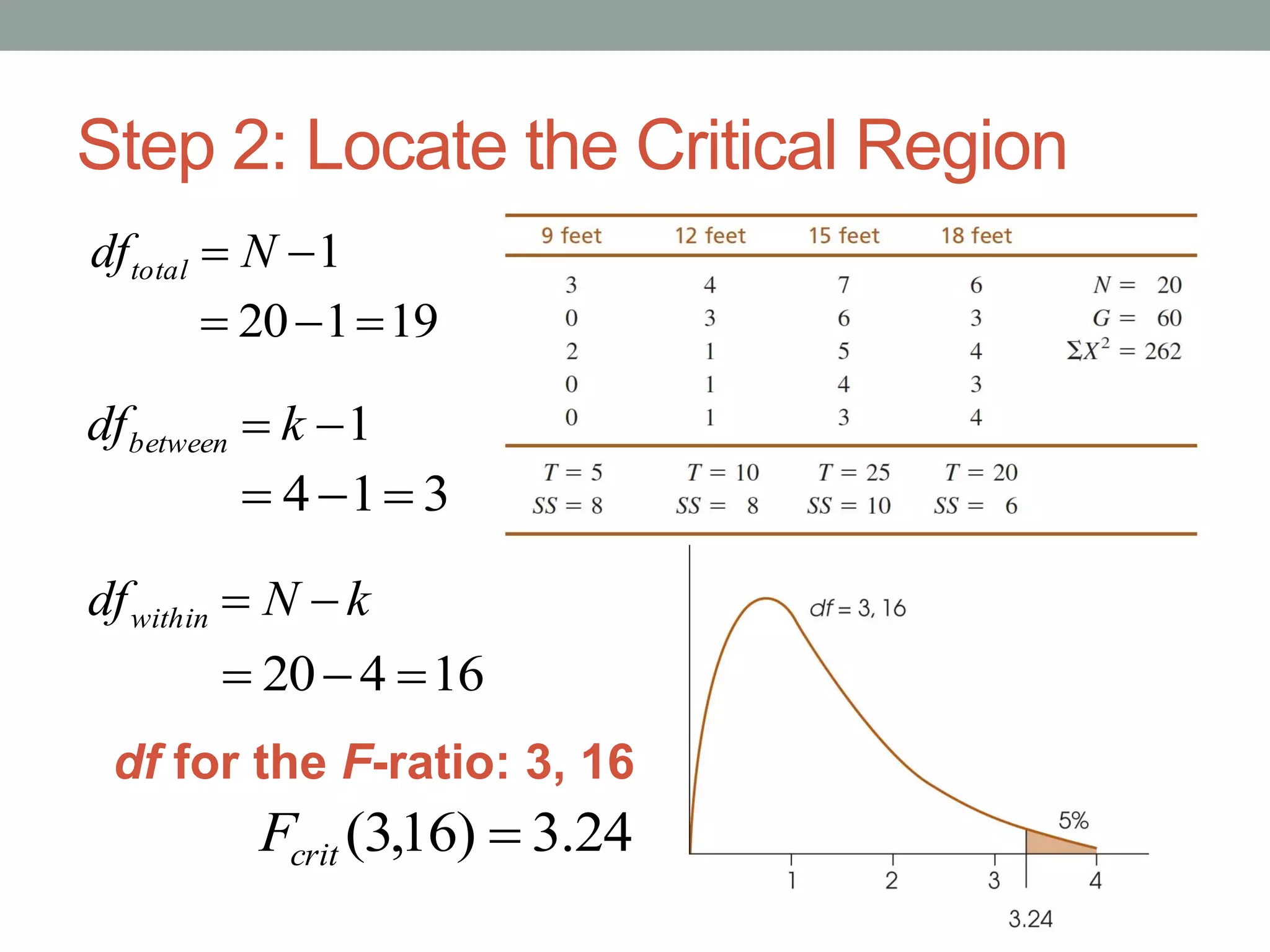
This document provides an introduction to analysis of variance (ANOVA). It discusses previous statistical tests learned, the logic and calculations of ANOVA, and examples of hypothesis testing using ANOVA. ANOVA allows comparison of three or more population means using their sample means. It partitions total variability into two components - variability between groups and variability within groups. The F-ratio compares the two and is evaluated to determine if there are statistically significant differences between population means. Post hoc tests are used after a significant F-ratio to determine exactly which group means differ.

1. CHAPTER 12
Introduction to
Analysis of Variance
(ANOVA)
ANOVA

2. What have we learned so far?
z-statistic Tests a claim about a population mean with a
sample mean (and σ is known)
One-sample
t-statistic
Tests a claim about a population mean with a
sample mean (σ unknown)
Independent-
measures
t-statistic
Tests a claim about the difference between two
population means by using two samples and
evaluating their mean difference

3. Rogers, Kuiper,
& Kirker (1977)
An experiment demonstrating the effect of
levels of processing (superficial to deep) on
memorization of events
• All participants were given a surprise memory test
• They were not told beforehand that they needed to
memorize the words on the list
Treatment 1
Population 1
Treatment 2
Population 2
Treatment 3
Population 3
Treatment 4
Population 4
Superficial
processing
Deep
Processing
Physical
characteristic
Sound
characteristic
Meaning Relation to
Self
How do we evaluate
differences between
4 different means?

4. Analysis of Variance!
• Tests claims about mean differences between two or
more populations by using two or more samples
• The tested hypothesis is very similar to the independent-
measures t-statistic, but now can be applied when we
have more than two groups
How do we evaluate
differences between
4 different means?

5. ATypical Example of a Situation
Requiring ANOVA
• t-tests only allow the comparison of 2 means at a time
• This would require 3 separate t-tests with 3 separate α-
levels, which accumulate over a series of tests
• ANOVA allows the evaluation of all three means at once

6. Terminology in ANOVA
• The variable that designates the groups being compared is called a
factor (e.g., “telephone condition,” “age”)
• The individual conditions or values that make up a factor are called
levels of the factor (e.g., 3 telephone conditions, 3 age groups)
No phone Hands-free Hand-held
Independent Variable:
Telephone conditions
Three treatment
conditions are created
by the researcher
6-yr-olds 8-yr-olds 10-yr-olds
Quasi-Independent
Variable: Age
Non-manipulated variable
used to create groups

7. Research Designs for ANOVA
• Independent-measures design
• Uses a separate group of participants for each of the treatment
conditions being compared
• Repeated-measures design
• Uses one group of participants for all of the treatment conditions
• Two-factor (or Factorial) design
• To be covered in Chapter 14

8. Statistical Hypotheses for ANOVA
• All populations have the same mean
(there is no mean difference between any of the groups)
• Telephone condition has no effect on driving performance
held-handfree-handsphoneno0 :  H
The Null
Hypothesis
No phone Hands-free Hand-heldTelephone
conditions

9. Statistical Hypotheses for ANOVA
No phone Hands-free Hand-heldTelephone
conditions
• At least one of the population means is different from
another (no specific decision which or how they differ)
• Not all treatment conditions are the same, there is a
treatment effect somewhere
The Alternative
Hypothesis
:1H There is at least one mean difference among populations

10. The Alternative Hypothesis
held-handfree-handsphoneno0 :  H
held-handfree-handsphoneno0 :  H
held-handfree-handsphoneno0 :  H

11. The Test Statistic for ANOVA
(error)chancebyexpectedDifference
meanssampleobetween twdifferenceObtained
t
The F-ratio
• A ratio of two sample variances
• a.k.a. mean squares, or MS values
• The same basic structure as the independent-measures t
statistic:
obtained mean differences (including treatment effects) MSbetween
F = ────────────────────────────────── = ───────
differences expected by chance (without treatment effects) MSwithin

12. Why Variance vs. Mean Differences?
However, we can evaluate the variance between these
three means:
A small variance represents small differences between the sample means
When we have
more than two
sample means,
how do you
evaluate a mean
difference?
It’s problematic
624.15
2
247.31
13
3
)4.72(
5.1778
1
2
2






n
SS
s

13. Type I Errors and Multiple-Hypothesis Tests
Why not just use multiple t-tests?
• Each time we conduct a t-test, we risk a Type I error
• The level of risk for making a Type I error is set by our α-level
• For an IV (telephone conditions) with three levels (none,
hands-free, hand-held), we would need three separate
t-tests
1. None v. hands-free; α = .05
2. None v. hand-held; α = .05
3. Hands-free v. hand-held; α = .05
• Each test compounds the chance of making an experiment-
wide Type I error
With ANOVA, we maintain an α = .05

14. CHAPTER 12.2
The Logic of ANOVA

15. The
Logic of
ANOVA
• Three steps:
1. Calculate between-treatments variance
1. Here we see that there is large variance between
sample means
2. Calculate within-treatment variance
1. There is some variability in scores within each
sample
3. Calculate the F-ratio to compare the two
variances
These scores are all
different. Or, in
statistical terms, these
scores are all variable.
Our goal is to measure
the amount of
variability to explain
why the scores are
different

16. This is Analysis of Variance, people!
Between-Treatments Variance
“Good” variance
• This is the variance we are
interested in
• Differences between samples
• Possible sources of
variance:
• Differences caused by
treatment
• Random chance
• How do participants in
different conditions differ?
Within-Treatments Variance
“Bad” variance
• Variance due to chance
and sampling error
• “Noise”
• How big are the
differences between
individuals when there is
no treatment effect?
• How do participants within
the same condition differ?

17. A Graphic Illustration

18. The F-ratio: ANOVA’s Test Statistic
Variance between treatments
Variance within treatments
Treatment effect + differences due to chance
Differences due to chance
F
• The denominator is our error term (variance expected due
to chance)
• When the treatment effect is zero (we cannot reject the
null), the F-ratio approximates 1

19. CHAPTER 12.3
ANOVA Notation and Formulas

20. ANOVA
Notation
• k = the number of levels of the factor
• n = the number of scores in each treatment
• N = the total number of scores in the study
• T = the sum of scores (∑X) for a specific treatment
• G = the sum of all scores (∑T) in the study
The textbook authors note that
they have introduced the
notations “T” and “G”
• “T” = “Treatment Total”
• “G” = “Grand Total”
Other sources may use
different notations.

21. The Nine Calculations for ANOVA

22. Computing Variance in ANOVA
• Since we are interested in different types of
variance, computations will be different from:
• Now we need to compute:
• SS and df for between treatments variance
• SS and df for within treatments variance
To do this, we will
first compute the
total SS and df,
and see how to
partition it into these
two components
df
SS
s 2

23. Calculating Total SS (SStotal)
• This is how we’ve
been computing SS for
t-tests:
• This is how we
compute Total SS for
ANOVA:
G = the sum of all scores in the study
 
N
X
XSS
2
2  
N
G
XSStotal
2
2
 

24. SStotal = SSbetween treatments + SSwithin treatments
• The product of the computation
for SStotal is the same as the sum
of SSbetween and SSwithin
N
G
XSStotal
2
2
 
 
N
G
n
T
SSbetween
22
treatmenteachinwithin SSSS ..
withintotalbetween SSSSSS 

25. Calculating Degrees of Freedom (df)
• This is how we’ve
been computing df so
far:
• This is how we
compute Total df for
ANOVA:
1 ndf 1 Ndftotal

26. dftotal = dfbetween treatments + dfwithin treatments
• The product of the computation for
dftotal is the same as the sum of
dfbetween + dfwithin
1 kdfbetween )1(  ndfwithin
menteach treatindfdfwithin 
kNdfwithin 
1 Ndftotal

27. Calculating Variances (Mean Squares)
• We now need the between treatment and within treatment
variances
• or mean of the squared deviations, a.k.a. Mean Squares
between
between
betweenbetween
df
SS
sMS  2
within
within
withinwithin
df
SS
sMS  2

28. The F-ratio
• The F-ratio compares the two variances we’ve computed
within
between
within
between
MS
MS
s
s
F  2
2
• Two characteristics of the F-ratio:
• It is always a positive number (there are no negative variances)
• When H0 is true, MSbetween and MSwithin are almost the same size

29. ANOVA Summary Table
• Comprehensively summarizes all important
elements in the calculation, and allows you to
check your work
Source SS df MS
Between treatments 30 2 15 F = 11.28
Within treatments 16 12 1.33
Total 46 14

30. CHAPTER 12.4
The Distribution of F-ratios

31. We have the F-statistic – what now?
• Now we have a test statistic that gives us a ratio of the
differences between treatments to differences attributed to
error
• To evaluate this statistic, we must consider our α-level
and consult the F-distribution table (up next)
• We compare this statistic to some critical value that defines
“unlikely” events in the F-distribution

32. The F-distribution
• Exact shape will change
with df
• df between (numerator)
• df within (denominator)
• Two characteristics of F:
• It is always a positive
number (there are no
negative variances)
• When H0 is true, MSbetween
and MSwithin are almost the
same size (equal to or
close to 1)

33. The F Distribution Table (pp. 705-707)

34. CHAPTER 12.5
Examples of Hypothesis Testing and Effect Size with
ANOVA

35. Hypothesis Testing Using ANOVA
We have more than 2 groups of data to compare
(independent measures, one-factor)
1. State H0 and H1
2. Set the alpha level and locate the critical region
1. Compute df (total, within, between)
3. Compute the F-ratio
1. Compute SS (total, within, between)
2. Compute MS (between, within)
3. Compute F
4. Make a decision
• Either “reject” or “fail to reject” H0

36. Example 12.1
• Are there any differences in satisfaction with different
viewing distances of a 42-inch HDTV?

37. Step 1: State your hypotheses and set α
• There is no effect of viewing distances on ratings of
satisfaction of watching HDTV
43210 :  H
differentismeanstheofoneleastat:1H
• There is an effect of viewing distances on ratings of
satisfaction of watching HDTV
05.0

38. Step 2: Locate the Critical Region
df for the F-ratio: 3, 16
1 kdfbetween
kNdfwithin 
1 Ndftotal
19120 
314 
16420 
24.3)16,3( critF

39. Step 3: Compute the F-ratio
• Remember this guideline - we start from the bottom up

40. Analyze the SS to get SSbetween and SSwithin
• SStotal is the SS for the total set
of N = 20 scores
N
G
XSStotal
2
2
 
withintotalbetween SSSSSS 
treatmenteachinwithin SSSS ..
20
60
262
2

20
360
262 82180262 
• SSwithin combines the SS values from each treatment condition
3261088 
• SSbetween since we already computed Sstotal and SSwithin::
503282 

41. Next we calculate MS

42. Calculation of MS: MSbetween and MSwithin
between
between
between
df
SS
MS 
within
within
within
df
SS
MS 
3
50
 67.16
16
32
 00.2

43. Compute the F-ratio
33.8
00.2
67.16

within
between
MS
MS
F

44. The Summary Table for Example 12.1
Source SS Df MS
Between
treatments
50 3 16.67 F = 8.33
Within
treatments
32 16 2.00
Total 82 19

45. Make a Decision Regarding H0
Our Critical F (Fcrit)
• Our F statistic falls in the critical region
• Our computed F (8.33) has a larger value than our critical F (3.24)
• Reject the null hypothesis
• It is very unlikely (p < .05) that we would obtain a value this large if
H0 is true. Therefore we reject the null hypothesis and conclude
that there is a significant effect of viewing distance on pleasure in
HDTV
Our Computed F
24.3)16,3( critF 33.8)16,3( F
05.0,33.8)16,3(  pF

46. What if there are unequal sample sizes in
my different groups?
• Sample variance contributes to our estimate of
error in the denominator
• What did we do when we had unequal sample
sizes with the independent-measures t-test?
Pooled variance: we do the same with ANOVA
k
k
within
within
within
dfdfdf
SSSSSS
df
SS
MS



...
...
21
21

47. CHAPTER 12.6
Post Hoc Tests

48. Measuring effect size for ANOVA
A significant difference indicates our difference is
larger than expected by chance, but does not tell
us how large this difference is
η² = the percentage of variance accounted for
total
between
SS
SS
2


49. What if I have a significant F-ratio?
Reject the null hypothesis. There is a significant
difference somewhere between at least two of the
groups (not all groups are equal)
But I don’t know where the difference is
If I have three groups:
Group A could be different than B
or group B from C
or group A from C.
So, if there is a significant F-ratio,
more tests must be done
to find which groups are different

50. Post hoc tests
Additional hypothesis tests that are done after an
ANOVA results in a significant F-ratio to determine
exactly which mean differences are significant and
which are not
• Finds where the significant differences are
• Developed to control the experiment-wise error
rate
Tukey’s Honestly Significant Difference (HSD)
Scheffé Test

51. Tukey’s HSD
Tells us the minimum difference between treatment
means that is necessary for significance
q: “Studentized range statistic” found in Table B.5
Must know k, df within treatments, and set α
n: number of scores in each treatment (requires
equal sample sizes in all groups)
n
MS
qHSD within


52. Scheffé Test
• More conservative than Tukey’s HSD
• Uses the ANOVA formula, but only compares two
groups at a time
• The denominator will remain the same as the overall
ANOVA (MS within), but the numerator will be
recalculated based only on the two groups in question
Start with the two groups that have the largest
mean difference, and work down until you have a
non-significant result

53. For the Scheffé Test:
• SS between treatments (and MS between) is recalculated
using only the two groups in question
• MS within remains the same from the overall ANOVA test
within
between
between
between
between
between
MS
MS
F
df
SS
MS
N
G
n
T
SS


 
22
Use the same critical value
as the overall ANOVA,
even though we now
only are comparing two
groups

54. Additional ANOVA steps:
8. Compute η² if necessary
9. Compute post-hoc tests if necessary to determine
where significant differences between groups are
located
10. Make some sort of overall statement summarizing all
the results of your study