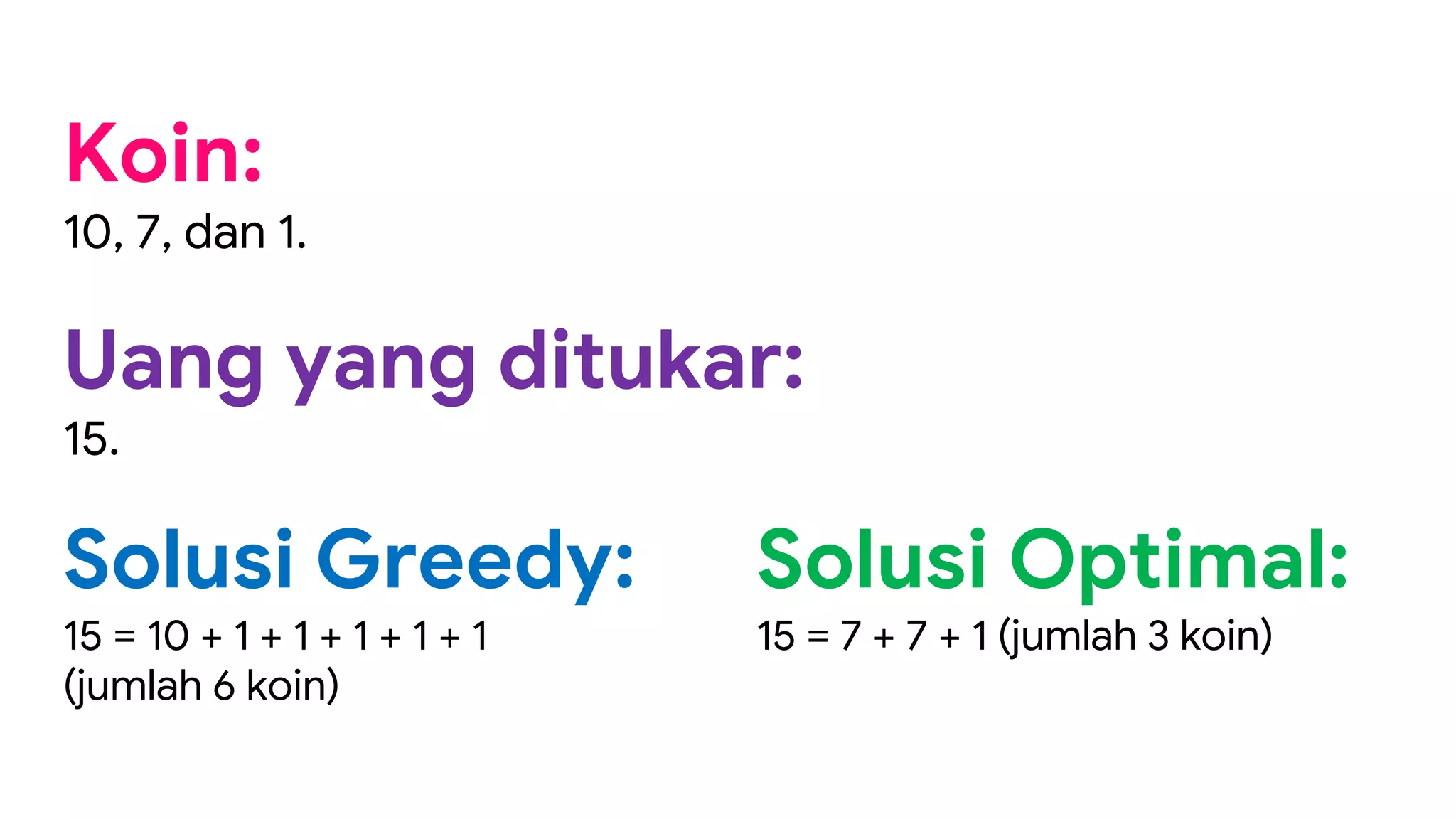
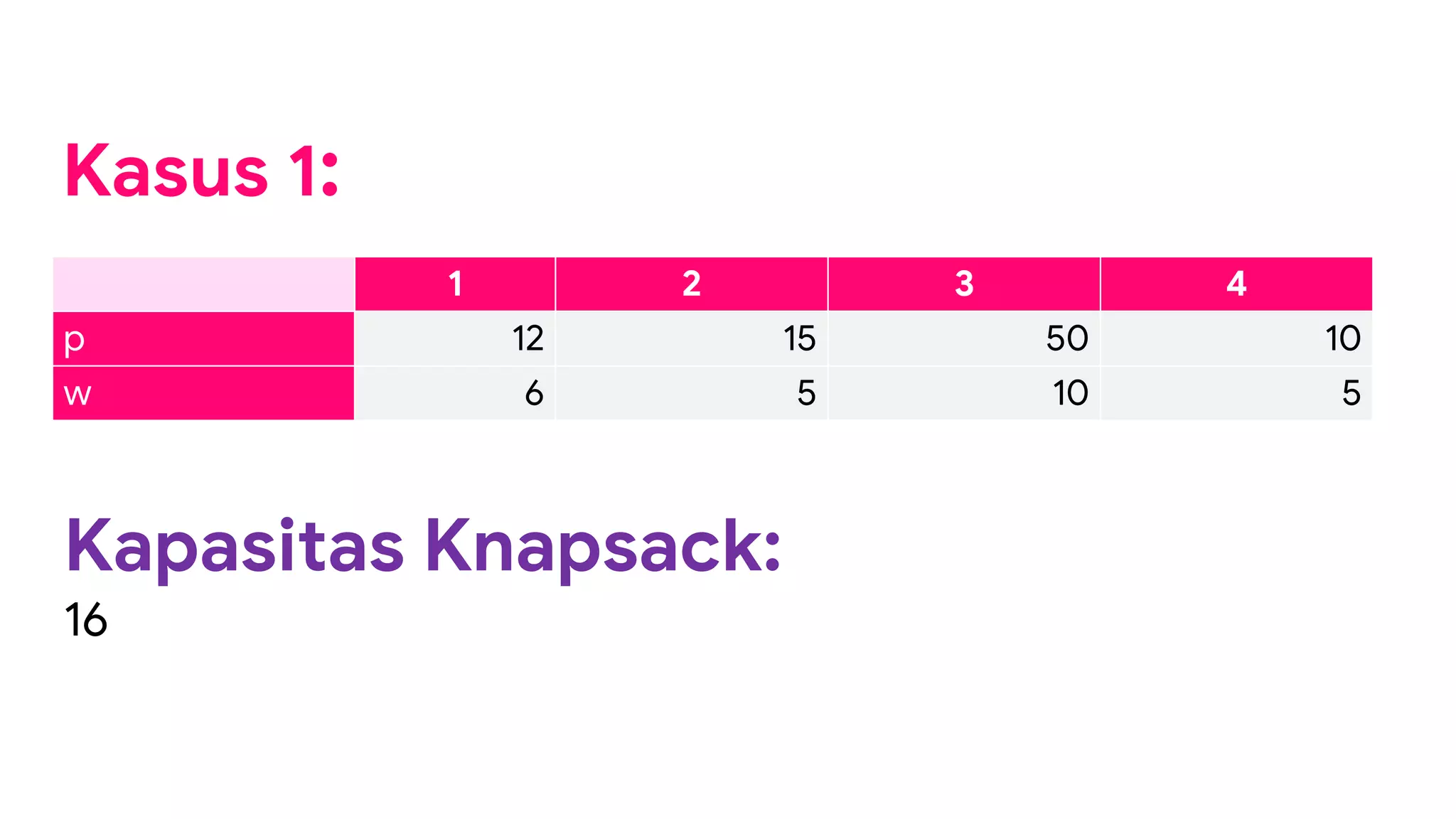
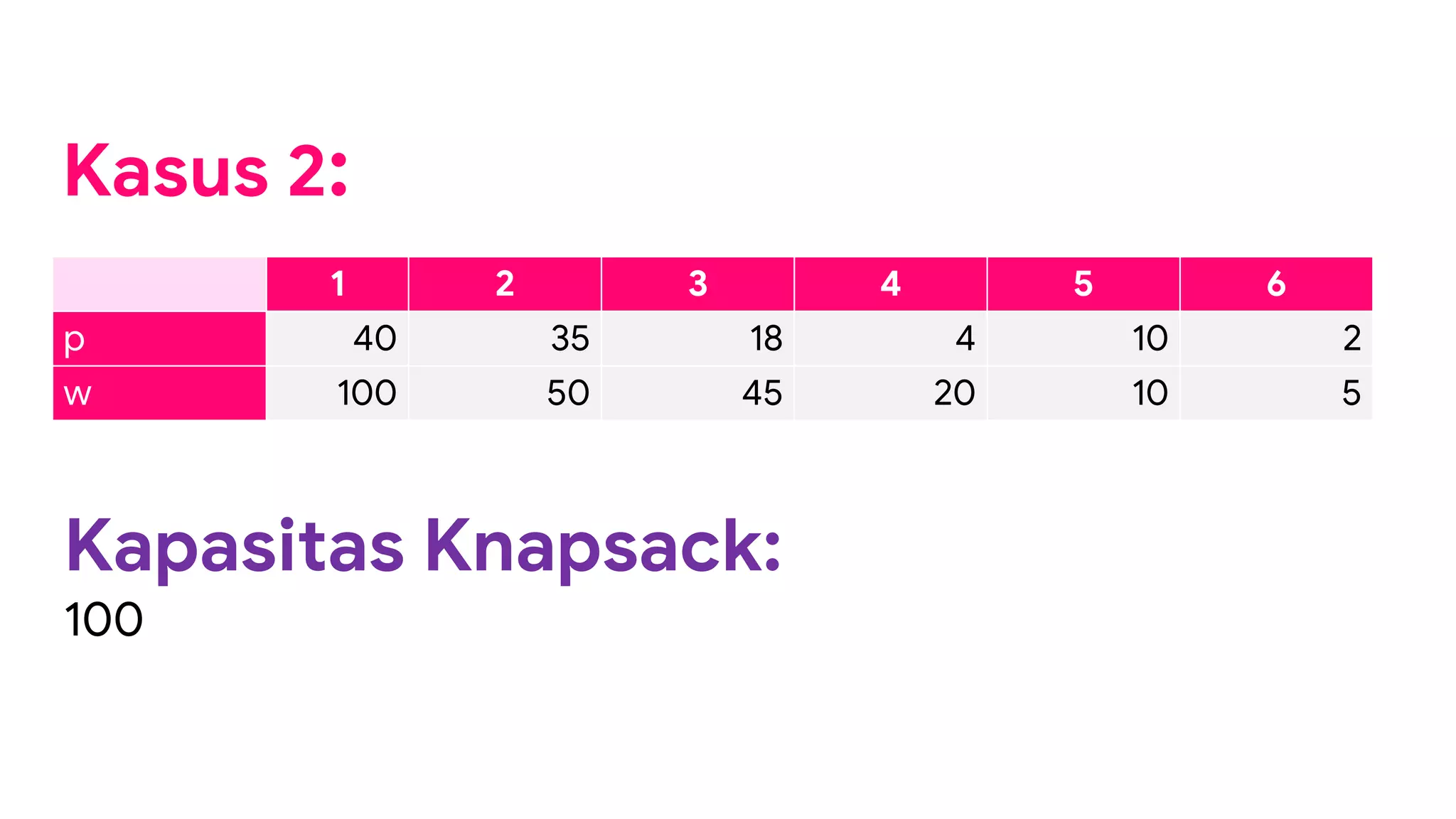
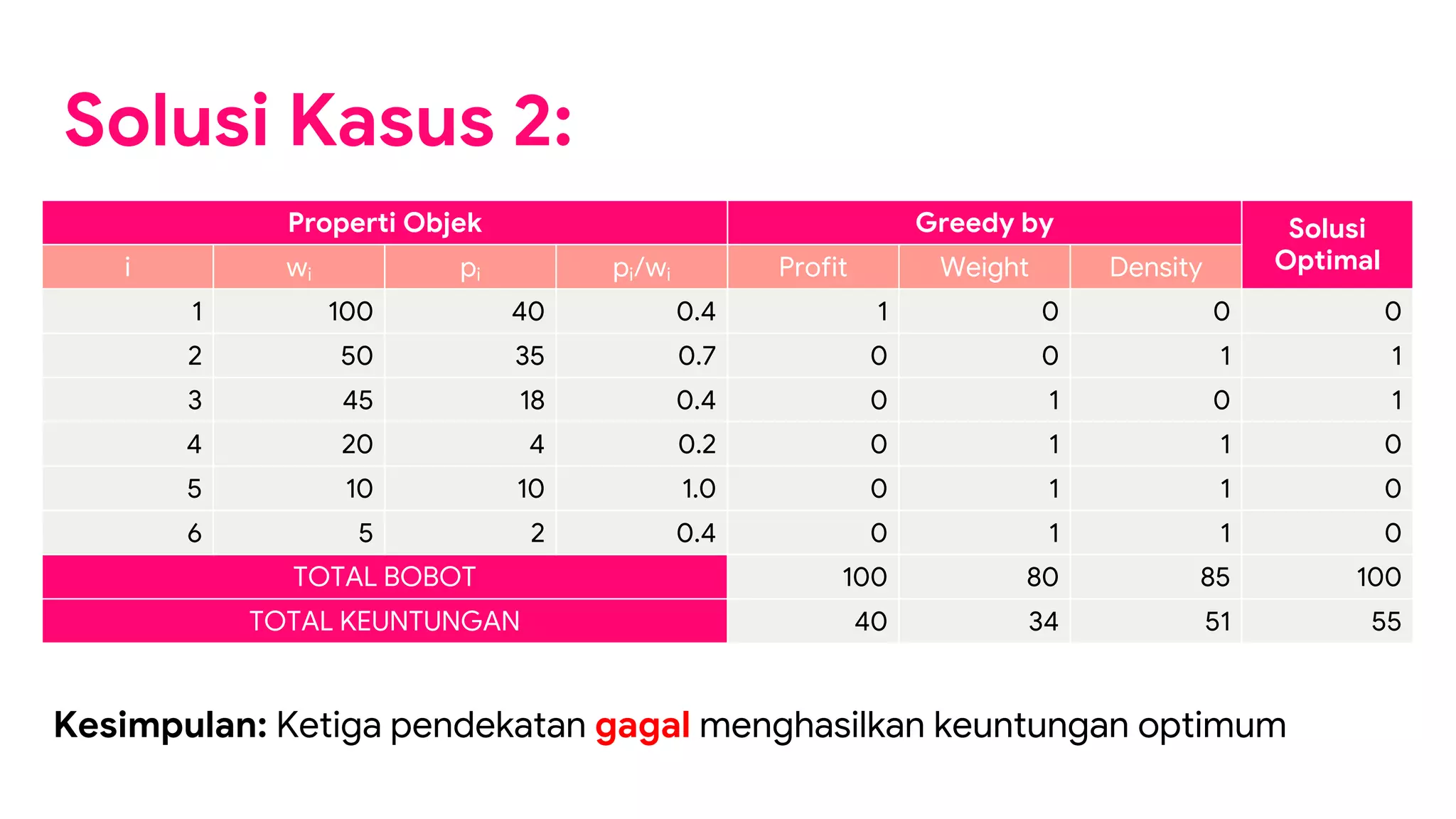
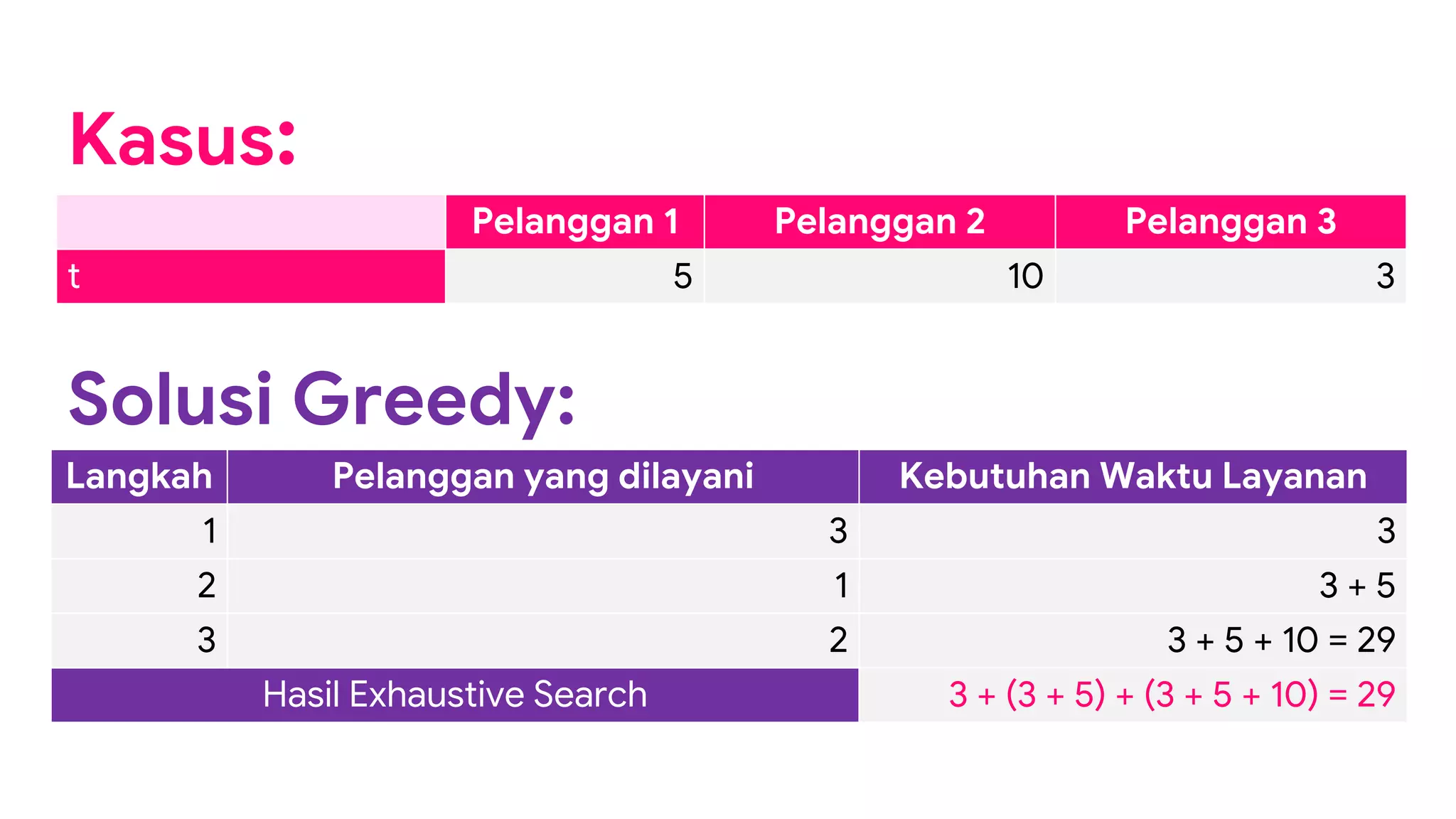
Dokumen ini membahas strategi algoritma greedy sebagai pendekatan untuk menyelesaikan permasalahan optimasi, menyoroti karakteristik, kelebihan, dan kelemahan dari metode ini. Beberapa contoh penerapan algoritma greedy seperti penukaran uang, knapsack 1/0, dan pelayanan antrian disajikan untuk menjelaskan penggunaannya dalam mencari solusi optimal. Meskipun seringkali memberikan solusi hampiran yang baik, algoritma greedy tidak selalu menjamin solusi paling optimal.

1. ANALISIS ALGORITMA
Strategi Algoritma: Greedy
Pemateri:
Adam Mukharil Bachtiar
adam@email.unikom.ac.id

2. Selain Brute Force terdapat
strategi algoritma lain yaitu
Greedy.

3. Strategi Greedy dikenal popular
untuk menyelesaikan
permasalahan optimasi.

4. Permasalahan optimasi sendiri
dibagi menjadi dua yaitu
maksimasi dan minimasi.

5. Greedy:
Sebuah pendekatan yang membentuk solusinya langkah
perlangkah dan dalam setiap langkah ada hal yang harus
dieksplorasi untuk menentukan pilihan terbaik.

6. Karakteristik:
1 Greedy memiliki prinsip “Take what you can get now”
2 Pada setiap langkah yang dikerjakan greedy, diambil solusi optimum local
dengan harapan langkah sisanya menuju ke arah solusi optimum global.
3 Greedy = Rakus, tamak.

7. (+):
Jika permasalahan yang dihadapi tidak membutuhkan
jawaban terbaik mutlak maka strategi ini seringkali optimal
dalam menghasilkan solusi hampiran dan dapat dibuktikan
secara matematis.

8. (-): Solusi optimum global belum tentu solusi optimum terbaik
tetapi bisa jadi pseudo-optimum.

9. Untuk menyelesaikan masalahnya,
Greedy mempunyai beberapa
elemen yang harus diidentifikasi.

10. 1 Himpunan kandidat (C)
2 Himpunan solusi (S)
3 Fungsi Seleksi
4 Fungsi Kelayakan
5 Fungsi Objektif
Elemen Greedy
yang harus
diidentifikasi

11. Skema Umum
Greedy

12. Problem 1: Penukaran Uang

13. Problem/Kasus:
Diberikan uang senilai A. Tukar A dengan koin-koin uang yang ada.
Berapa jumlah minimum koin yang diperlukan untuk penukaran
tersebut?
Jenis Kasus:
Minimasi

14. Himpunan Kandidat:
Himpunan koin yang merepresentasikan nilai 1, 5, 10, 25, paling
sedikit mengandung satu koin untuk setiap nilai.
Himpunan Solusi:
Total nilai koin yang dipilih tepat sama jumlahnya dengan nilai uang yang
ditukarkan.
Fungsi Seleksi:
Pilihlah koin yang bernilai tertinggi dari himpunan kandidat yang tersisa.

15. Fungsi Layak:
Memeriksa apakah nilai total dari himpunan koin yang dipilih tidak
melebihi jumlah uang yang harus dibayar.
Fungsi Objektif:
Jumlah koin yang digunakan minimum.

16. Koin:
5, 4, 3, 2, dan 1.
Uang yang ditukar:
7.
Solusi Greedy:
7 = 5 + 1 + 1 (jumlah 3 koin)
Solusi Optimal:
7 = 4 + 3 (jumlah 2 koin)

17. Koin:
10, 7, dan 1.
Uang yang ditukar:
15.
Solusi Greedy:
15 = 10 + 1 + 1 + 1 + 1 + 1
(jumlah 6 koin)
Solusi Optimal:
15 = 7 + 7 + 1 (jumlah 3 koin)

18. Koin:
15, 10, dan 1.
Uang yang ditukar:
20.
Solusi Greedy:
20 = 15 + 1 + 1 + 1 + 1 + 1
(jumlah 6 koin)
Solusi Optimal:
20 = 10 + 10 (jumlah 2 koin)

19. Solusi optimal didapatkan dengan
konsep Exhaustive Search.

20. Agar pemilihan koin berikutnya optimal
maka perlu mengurutkan himpunan
koin dalam urutan menurun.

21. Jika himpunan koin sudah terurut
menurun maka kompleksitas algoritma
Greedy menjadi !(#).

22. Problem 2: 1/0 Knapsack

23. Solusi 1/0 knapsack menggunakan
Greedy dengan Greedy Heuristic.

24. Greedy by profit:
Pada setiap langkah, pilih objek yang mempunyai keuntungan
terbesar.
Greedy by weight:
Pada setiap langkah, pilih objek yang memiliki beban teringan.
Greedy by density:
Pada setiap langkah, knapsack diisi dengan objek yang memiliki ⁄"#
$%
yang terbesar

25. Semua pendekatan tersebut sama-sama
bertujuan memaksimalkan keuntungan
dengan cara yang berbeda (maksimasi).

26. Kasus 1:
Kapasitas Knapsack:
16
1 2 3 4
p 12 15 50 10
w 6 5 10 5

27. Solusi Kasus 1:
Properti Objek Greedy by Solusi
Optimali wi pi pi/wi Profit Weight Density
1 6 12 2 0 1 0 0
2 5 15 3 1 1 1 1
3 10 50 5 1 0 1 1
4 5 10 3 0 1 0 0
TOTAL BOBOT 15 16 15 15
TOTAL KEUNTUNGAN 65 37 65 65
Solusi optimal X = (0,1,1,0)
Kesimpulan: Greedy by profit dan density yang memberikan solusi optimal

28. Kasus 2:
Kapasitas Knapsack:
100
1 2 3 4 5 6
p 40 35 18 4 10 2
w 100 50 45 20 10 5

29. Solusi Kasus 2:
Properti Objek Greedy by Solusi
Optimali wi pi pi/wi Profit Weight Density
1 100 40 0.4 1 0 0 0
2 50 35 0.7 0 0 1 1
3 45 18 0.4 0 1 0 1
4 20 4 0.2 0 1 1 0
5 10 10 1.0 0 1 1 0
6 5 2 0.4 0 1 1 0
TOTAL BOBOT 100 80 85 100
TOTAL KEUNTUNGAN 40 34 51 55
Kesimpulan: Ketiga pendekatan gagal menghasilkan keuntungan optimum

30. Problem 3: Pelayanan Antrian

31. Problem/Kasus:
Sebuah server (dapat berupa processor, pompa, kasir di bank, dll)
mempunyai n pelanggan (customer, client) yang harus dilayani.
Waktu pelayanan untuk setiap pelanggan i adalah ti.
Jenis Kasus:
Minimasi

32. Kasus:
Solusi Exhaustive Search:
Pelanggan 1 Pelanggan 2 Pelanggan 3
t 5 10 3
Urutan Kebutuhan Waktu Layanan
1à2à3 5 + (5 + 10) + (5 + 10 + 3) = 38
1à3à2 5 + (5 + 3) + (5 + 3 + 10) = 31
2à1à3 10 + (10 + 5) + (10 + 5 + 3) = 43
2à3à1 10 + (10 + 3) + (10 + 3 + 5) = 41
3à1à2 3 + (3 + 5) + (3 + 5 + 10) = 29
3à2à1 3 + (3 + 10) + (3 + 10 + 5) = 34
Optimal

33. Penyelesaian dengan Exhaustive Search
seperti tadi membutuhkan kompleksitas
sebesar !(#. #!).

34. Dengan strategi Greedy, pada setiap
langkah pilih pelanggan yang
membutuhkan waktu terkecil di antara
pelanggan lain yang belum terlayani.

35. Kasus:
Solusi Greedy:
Pelanggan 1 Pelanggan 2 Pelanggan 3
t 5 10 3
Langkah Pelanggan yang dilayani Kebutuhan Waktu Layanan
1 3 3
2 1 3 + 5
3 2 3 + 5 + 10 = 29
Hasil Exhaustive Search 3 + (3 + 5) + (3 + 5 + 10) = 29