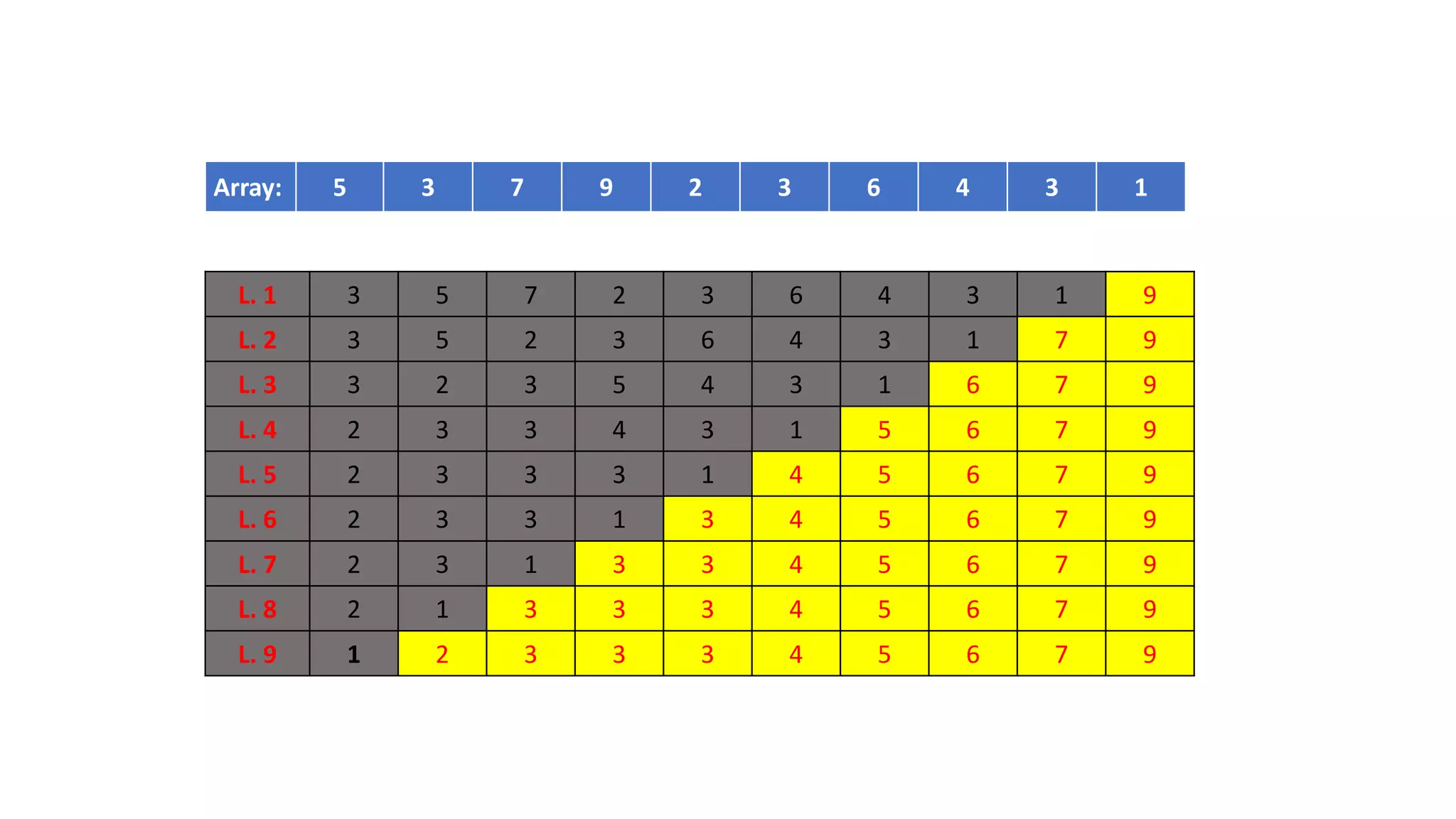
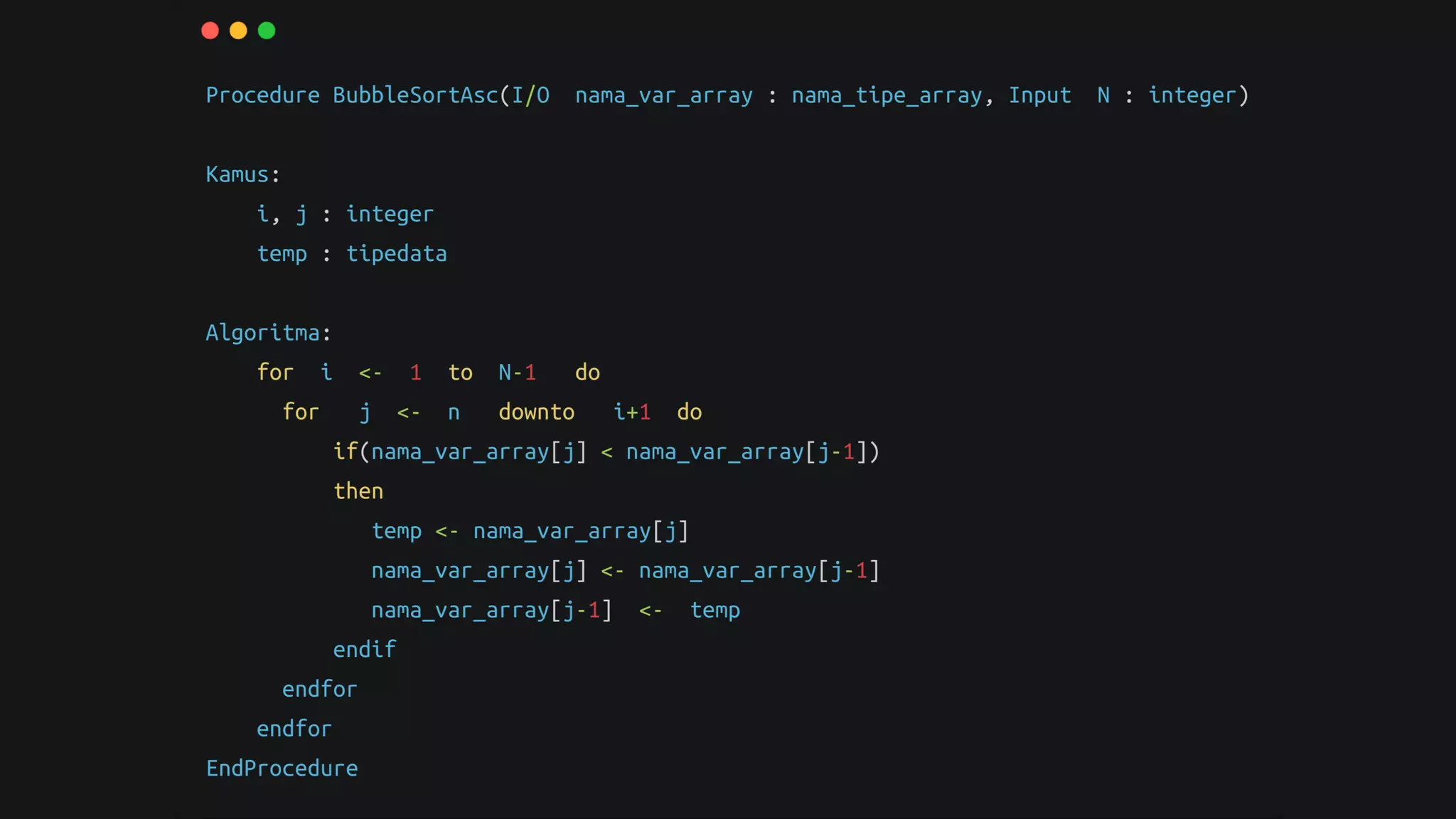
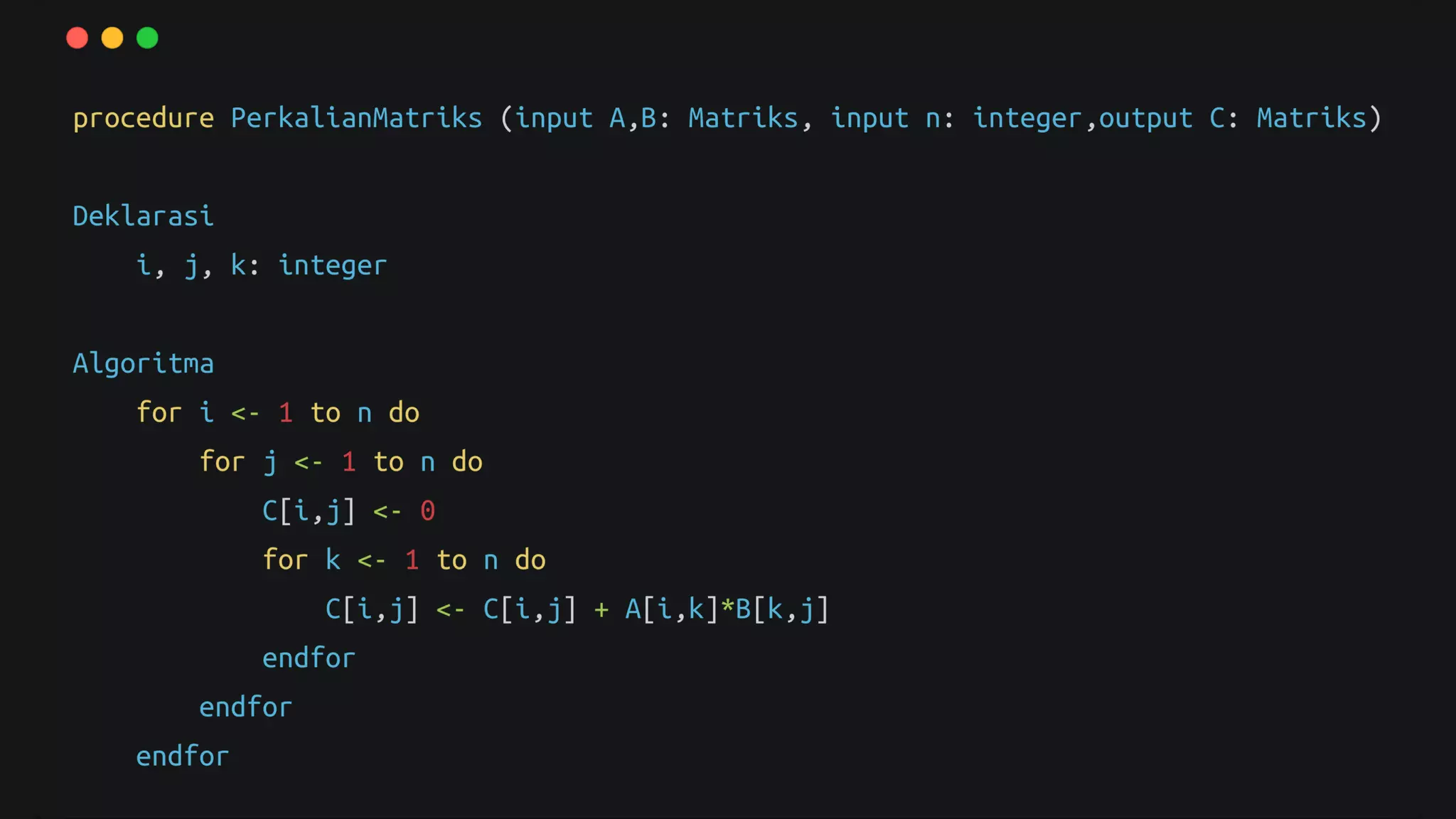
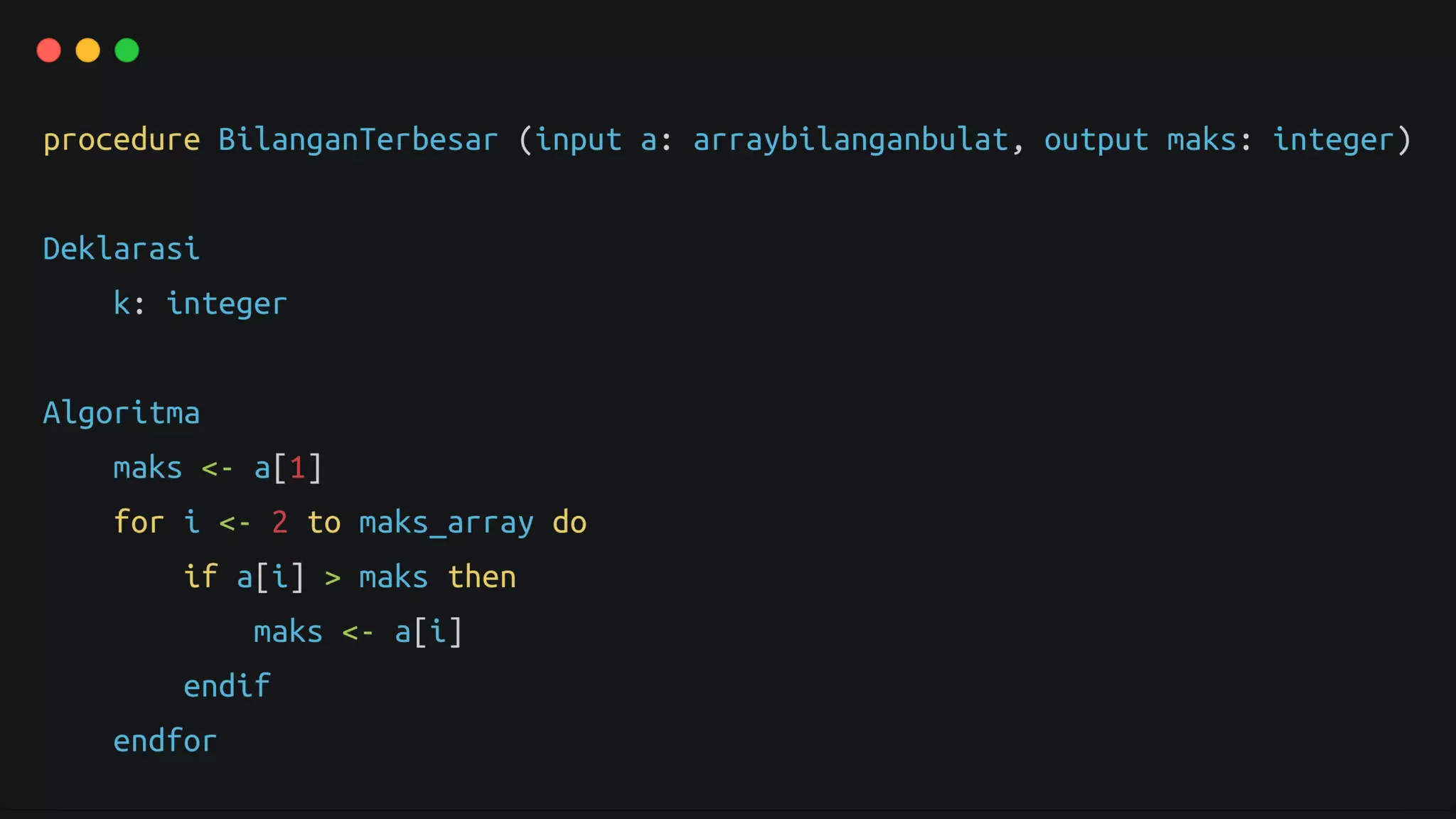
Dokumen ini membahas algoritma brute force sebagai strategi dasar dalam pemecahan masalah, dengan karakteristik yang cenderung sederhana dan mudah diimplementasikan. Meskipun memiliki kekurangan seperti lambat dan tidak kreatif, brute force dapat digunakan untuk beberapa masalah penting seperti pencarian dan pengurutan. Beberapa contoh penerapannya juga disertakan dalam dokumen.

1. ANALISIS ALGORITMA
Strategi Algoritma: Brute Force
Pemateri:
Adam Mukharil Bachtiar
adam@email.unikom.ac.id

2. Setelah memahami kompleksitas
suatu algoritma maka kita bisa
mengusahakan agar kompleksitas
tersebut lebih efisien.

3. Untuk bisa memahami efisiensi
kompleksitas maka kita harus
memahami strategi algoritma
terlebih dahulu.

4. Ada beberapa strategi algoritma yang
digunakan pada algoritma dan salah
satunya adalah brute force.

5. Brute Force:
Sebuah pendekatan yang lempang (straightforward) untuk
memecahkan masalah yang didasarkan pada pernyataan
masalah dan definisi konsep yang dilibatkan.

6. Karakteristik:
1 Umumnya tidak cerdas dan tidak mangkus (terkadang disebut sebagai
Naïve Algorithm).
2 Seringkali dijadikan landasan untuk mencari strategi lain yang lebih
efisien dan optimal.
3 Mudah untuk diimplementasikan karena kesederhanaannya.

7. (+):
1 Dapat digunakan untuk memecahkan sebagian besar masalah.
2 Sederhana dan mudah dimengerti.
3 Menghasilkan algoritma yang layak untuk beberapa masalah penting
seperti pencarian, pengurutan, pencocokan string, dan perkalian matriks
3 Menghasilkan algoritma baku untuk tugas-tugas komputasi seperti
penjumlahan/perkalian n buah bilangan, menentukan elemen
minimum/maximum pada suatu list.

8. (-):
1 Jarang menghasilkan algoritma yang mangkus.
2 Beberapa algoritmanya lambat dan tidak bisa diterima.
3 Tidak sekreatif strategi lainnya.

9. Untuk bisa melihat strategi algoritma
Brute Force mari kita lihat beberapa
contoh penerapannya.
Untuk bisa melihat strategi algoritma
Brute Force mari kita lihat beberapa
contoh penerapannya.

10. Kasus 1: Menghitung operasi aritmatika

11. Problem:
Menghitung !"
(a>0, n adalah bilangan bulat tak negative)
Pola Pikir:
Kalikan 1 dengan a sebanyak n kali
!"
= !. !. !. … . ! (n kali), jika & > 0
= 1, jika & = 0

12. Problem:
Menghitung !! (n adalah bilangan bulat tak negative)
Pola Pikir:
Kalikan n buah bilangan, yaitu 1, 2, 3, … ,n bersama-sama
!! = 1 % 2 % 3 % … % !, jika ! > 0
= 1, jika ! = 0

13. Problem:
Menghitung perkalian dua matriks berukuran n x n
Pola Pikir:
Hitung setiap elemen hasil perkalian satu-persatu, dengan cara
mengalikan dua vektor yang panjangnya n
!"# = %"&'&# + %")')# + … + %"+'+#
= ∑-.&
+
%"-'-#

15. Problem:
Mencari bilangan terbesar pada suatu himpunan bilangan
Pola Pikir:
Anggap bilangan pertama adalah yang terbesar kemudian
bandingkan dengan bilangan lain satu-persatu, apabila lebih
besar bilangan lain maka jadikan bilangan tersebut bilangan
terbesar.

17. Kasus 2: Sequential Search

18. Given an array to be processed:
Number
Data that want to be sought : 9
• Number[1] = 9?
• Number[2] = 9?
• Number[3] = 9?
Result: 9 is found in number[3]
5 1 9 4 2
[1] [2] [3] [4] [5]
FOUND ß FALSE
FOUND ß FALSE
FOUND ß TRUE (STOP SEARCH)

19. Ada yang lebih
mangkus daripada
Brute Force?

20. Kasus 3: Bubble Sort

21. Array: 5 3 7 9 2 3 6 4 3 1
L. 1 3 5 7 2 3 6 4 3 1 9
L. 2 3 5 2 3 6 4 3 1 7 9
L. 3 3 2 3 5 4 3 1 6 7 9
L. 4 2 3 3 4 3 1 5 6 7 9
L. 5 2 3 3 3 1 4 5 6 7 9
L. 6 2 3 3 1 3 4 5 6 7 9
L. 7 2 3 1 3 3 4 5 6 7 9
L. 8 2 1 3 3 3 4 5 6 7 9
L. 9 1 2 3 3 3 4 5 6 7 9