An Exploration of Fractal Geometry

Running head: AN EXPLORATION OF FRACTAL GEOMETRY 1
An Exploration of Fractal Geometry:
The Mathematical Language of Nature
Marisa Hahn
Concordia University Wisconsin

AN EXPLORATION OF FRACTAL GEOMETRY 2
Abstract
In the following pages, fractals will be comprehensively examined. Fractal patterns found in the
natural world, including the British coastline paradox, will be used to introduce the concept of
the fractal. There will also be a brief history about the discovery of fractals involving
mathematicians like Georg Cantor and Benoit B. Mandelbrot. Properties of fractals such as
recursion, self-similarity, iteration, and the fractal dimension will be examined in depth, as well
as a brief look at the role of chaos in fractal geometry. All these definitions, concepts, and
properties of fractals will also be covered by examining some well-known fractals that include
the Sierpinski Triangle, the Cantor Set, and the Julia Set. Also, the Mandelbrot Set.
Keywords: fractal, recursion, iteration, self-similarity, fractal dimension, chaos

An Exploration of Fractal Geometry:
The Mathematical Language of Nature
The fractal is a unique topic in mathematics both because of its properties and because
the amount of research on the subject has increased exponentially since its recent discovery.
Compared to the rest of mathematics, the concept of a fractal is relatively new, having only been
identified and explored in detail in the last fifty years. Due to the work of mathematicians such as
Benoit Mandelbrot and because of the more advanced technology available in the 20th century,
fractals have become a unique topic of interest in the world of mathematics.
A fractal is unique in that there is no uniform definition that works for all fractals. The
term “fractal” was not even used until Mandelbrot coined it in the early 1970s (Lauwerier, 1991,
p.1). However, each fractal displays certain properties and characteristics which will be explored
in depth later on. Before that, the best way to introduce the concept of a fractal is to describe it as
“a geometrical figure that consists of an identical motif repeating itself on an ever-reducing
scale” (Lauwerier, 1991, p.1). In order to understand the mathematics behind this description,
four main properties and characteristics of fractals will be explored: recursion, iteration, self-
similarity, and fractal dimension, which is also called similarity dimension. After these four
concepts have been thoroughly explained, some famous fractals will be analyzed that include the
Koch Curve and the Julia Set.
History of Fractals
Before these properties are explored, a brief history will be covered about the
mathematicians who contributed to the founding of the fractal. As stated previously, the study of
fractals is relatively new to mathematics having only really developed in the last 50 years. Why
had it taken mathematicians so long to begin studying these complex geometric figures? Part of

the answer dates back to the Ancient Greeks. As long ago as 300 B.C. during Euclid’s lifetime,
mathematics had generally been conducted theoretically, and this had been especially true for
geometry. Theoretical mathematics, also called pure mathematics, used logical rules, principles,
theorems, axioms, etc. as the main means of reasoning (Lauwerier, 1991, p. 15). Then these
rules, theorem, and axioms would be formulated into proofs which became tools by which other
rules and theorems could be established. This process would repeat itself and has been how most
mathematics, particularly Euclidean geometry, has been conducted for thousands of years:
mathematical facts only arose when conducting proofs of older mathematical facts.
Some famous fractals such as the Cantor Set were discovered long before the 1970s, but
because there was no uniform study of fractals, mathematicians could only observe these figures
and the unusual characteristics they possessed. It wasn’t until pure mathematics fused with
experimental and observational science that horizons broadened for mathematicians like Benoit
Mandelbrot. He explained that mathematics must become like other natural sciences, where the
theoretical and experimental, although very different and even opposing to one another, must be
both be used and examined (Peitgen, Part One, 1992, p. 2-3).
Mandelbrot’s fascination with geometric figures and patterns began during his youth in
France as he became curious about the complexity in nature and the world he lived in (Bedford,
1998, p. 33). Then he began to materialize his thoughts and work while he was employed at a
business firm in the 1960s. While working at IBM, he looked at the patterns of graphed data for
electrical engineers and the relationship between the appearing random errors in communication
transmission (Gleick, 1987, p. 91). After many hours of research, Mandelbrot “discovered a
consistent geometric relationship between the bursts of errors and the spaces of clean
transmission,” and while the engineers were unsure of what he was talking about,

mathematicians immediately recognized similarity between Mandelbrot’s discoveries and the
famous Cantor Set, to be described in depth later (Gleick, 1987, p. 91-92). In the 1970s,
Mandelbrot continued to look at nature and tried to compare it to geometry. However, he knew
that mountains were not like cones and clouds were not like spheres, so he looked for actual
mathematics behind them (Bedford, 1998, p. 33).
Mandelbrot went on to study these patterns and geometrical relationships, and he wrote
the pioneering work entitled The Fractal Geometry of Nature in which he explains why he began
to study fractals. Responding to the criticism that geometry is boring, he explains that the
patterns found in nature such as clouds, mountains, coastlines, trees, etc. “are so irregular and
fragmented, that, compared with (Euclidian geometry), Nature exhibits not simply a higher
degree but an altogether different level of complexity,” and “the number of distinct scales of
length of natural patterns is for all practical purposes infinite” (Mandelbrot, 1977, p. 1). Another
reason that the study of fractals has risen dramatically in the past few decades is because of the
development of technology. Using our working description of fractals as “a geometrical figure
that consists of an identical motif repeating itself on an ever-reducing scale,” the computer
allows mathematicians to analyze fractals at magnitudes that would never have been possible
seventy years ago (Lauwerier, 1991, p.1).
Properties of Fractals
Why do fractals differ from traditional geometric figures? Fractals have extremely fine
structure, meaning that regardless of how much one zooms in or zoom out, there is always
infinitely more to see of the fractal (Bedford, 1998, 34). It is always increasing in complexity.
Also mentioned previously, each fractal is unique in that there is no one concrete definition for
all fractals, which is how most traditional geometric objects are described. For example, by

definition a triangle is a one-dimensional figure with three sides connected by three vertices, and
this statement holds true for any and all triangles. Contrarily, this is not the case with fractals
because there is no concrete definition that can be applied to each and every fractal, but rather,
there are common properties that fractals display (Bedford, 1998, p. 34). Benoit Mandelbrot
explains that fractal geometry is the language in which we describe parts of nature such as
clouds, lightning, trees, etc. (Peitgen, Animated Discussion, 1990). Consequently, some
properties and characteristics of fractals will be explained using some famous fractals as well as
examples from the nature.
Iteration
The first property of fractals to be explored is the property of iteration. It is imperative to
understand the feedback process, more specifically the process of geometric iteration which
involves “producing a sequence of geometric figures.” (Bedford, 1998, p. 33). The process of
feedback defined by the dynamic laws stablished by Newton and
Leibniz, allows for the explanation of feedback and iteration.
These dynamical laws “determine, for example, the location and
velocity of a particle at one time instant from its value at the
preceding instant” (Peitgen, Part One, 1992, p. 21). Therefore, iteration can be defined as
repeating an operation where the next input is the previous output (McGuire, 1991, p.14). The
process of feedback or iteration can be seen more easily in Figure 1.
Recursion
When talking about iteration as a repeating operation where the next input is the previous
output, recursion is that repeating operation that informs how the next stage of a figure will be
constructed. Fractals are usually defined by a process of recursion, or a repeating rule that can be
Figure 1: Iteration

simple or extremely complicated (Bedford, 1998, p. 34-35). Looking back at Figure 1, recursion
is the “process” that occurs during iteration. Recursion is also known as the replacement rule
because “one graphical object is replaced with another, which
is usually more complex, but which fits into the place of the
original” (McGuire, 1991, p. 14).
The famous fractal called the Sierpinksi Triangle, as seen in Figure 2, can be used to
illustrate recursion. The process or rule of this fractal could be that for every new stage, a
triangle is removed from inside each black triangle. This is done by connecting the midpoints of
each side of the black triangle and removing the resulting triangle. Iteration is also displayed in
the Sierpinski Triangle fractal because each new stage begins with the figure resulting from the
previous stage.
Self-Similarity
Another property that fractals display is self-similarity. In order to introduce the concept
of self-similarity, begin by looking at a tree outside or the tree in Figure 4 if there is no window
nearby. Start by looking at where the trunk meets the ground, and slowly bring your eyes up to
where the trunk starts to branch off. These two branches will then continue
for a while before each larger branch turns into many smaller branches,
and this process continues until the “ends” of the tree have tiny branches.
This is the concept of self-similarity. A figure is self-similar if part of the
figure contains a scaled down replica of itself (Lauwerier, 1991, p.2).
Looking again at the Sierpinski Triangle in Figure 2, one can see that each stage is made up of
exempt replicas of the previous stages. Because these replicas are exact, the figure is called
strictly self-similar. This fits the initial description of a fractal as “a geometrical figure that
Figure 2: Sierpinski Triangle
Figure 3: Tree

consists of an identical motif repeating itself on an ever-reducing scale” (Lauwerier, 1991, p.1).
This is because, as stated previously, “a figure is called self-similar if a part of the figure
contains on a smaller scale an exact replica of the whole” (Bedford, 1998, p. 36).
Fractal Dimension
In order to introduce the concept of fractal dimension, the question posed by Benoit
Mandelbrot will be explored in depth: “How long is the coastline of Great Britain?” (Peitgen,
Animated Discussion, 1992). To begin, a ruler representing 200 km is used to measure the entire
coastline, and it takes 13 of these rulers to measure the entire
coastline. Doing the multiplication, 13 rulers(
200 𝑘𝑚
1 𝑟𝑢𝑙𝑒𝑟
) means that
Britain’s coast is 2,600 km long. However, if the length of the
ruler used is halved, there are now 38 smaller rulers used
measuring 100 km each, and the total length of the coastline
now becomes 3,800 km (or 38 smaller rulers*
100 𝑘𝑚
1 𝑠𝑚𝑎𝑙𝑙𝑒𝑟 𝑟𝑢𝑙𝑒𝑟
). Continuing the process two more
times, 107 matchsticks representing 54 km each are now used to show that the coastline is 5,778
km long ( or 107 matchsticks*
54 𝑘𝑚
1 𝑚𝑎𝑡𝑐ℎ𝑠𝑡𝑖𝑐𝑘
). Once more, if the matchsticks are halved, it takes 320
half matchsticks measuring 27 km each to show the coastline is 8,640 km long (or 320 half
matchsticks*
27 𝑘𝑚
1 ℎ𝑎𝑙𝑓 𝑚𝑎𝑡𝑐ℎ𝑠𝑡𝑖𝑐𝑘
). This illustrates the mathematical concept that the length of a
smooth curve can be as precise as you want by measuring it with a smaller and smaller ruler,
because as you use smaller and smaller rulers to measure the coastline, you are able to include
more bays, islands, and capes (Peitgen, Animated Discussion, 1992).
In order to explore the connection mentioned above, the term dimension must be defined
mathematically. While there are many different notations used to define dimension, for the
Figure 4: British coast

purposes of understanding fractal dimension, the self-similarity definition of dimension will be
examined first. A loose definition of the term dimension would be “the number of coordinate
axes needed to determine the location of a point” (Bedford, 1998, p. 43). For example, a line in
space only requires one dimension, a plane requires two dimensions, and a figure such as a
sphere or cube requires three dimensions. What about a point in space? This has the dimension
of zero because, if it fills the entire space, no coordinates are needed to locate it (Bedford, 1998,
p.43). This takes a closer look at self-similarity dimension which involves self-similar figures, or
defined as being figures that are made up of smaller replicas of itself. The formula for dimension,
Reduction factorDimension=Replacement number will serve as a guide. (It will be abbreviated as
rD=n). What does this equation mean? If you begin with a “d-dimensional shape and enlarge it by
a factor r, then its d-dimensional volume is multiplied by rD“(Gowers, 2008, p. 57). After using
logarithms to solve for the dimension (D), the following is the
result:
log(rD)= log(n)
D log(r) = log(n)
D =
𝑙𝑜𝑔 (𝑛)
𝑙𝑜𝑔(𝑟)
=
𝑙𝑜𝑔 (𝑟𝑒𝑝𝑙𝑎𝑐𝑒𝑚𝑒𝑛𝑡 𝑛𝑢𝑚𝑏𝑒𝑟)
𝑙𝑜𝑔(𝑟𝑒𝑑𝑢𝑐𝑡𝑖𝑜𝑛 𝑓𝑎𝑐𝑡𝑜𝑟)
This will be illustrated using a cube, as shown in Figure 5 (Peitgen,
Part One, 1992, p. 231). Each smaller cube is self-similar to the larger cube. The reduction factor
would be 3 because the linear lengths are 1/3 of the original length of the cube, or the original
length is reduced by 3 (Peitgen, Part One, 1992, p. 231). Next, our replacement number would
be 27 because it is the quantity of smaller cubes needed to replace the original. Consequently,
using the formula above, the following conclusion is met:
Figure 5

Reduction factorDimension=Replacement number
3Dimension = 27
3Dimension = 33
Dimension = 3
Consequently, the result is that the dimension of a cube is three. One huge difference between
examining the dimensions of traditional Euclidian geometric figures, such as the cube, and
examining fractal dimension, is that fractals rarely display the dimension as a positive, whole
integer (Gowers, 2008, p. 57). When recalling Mandelbrot’s question of “How long is the
British coastline?” one can observe in Figure 6, it is clear to see that there is a relationship
between the number of rulers used and the reciprocal of the length of the ruler itself, or the
reduction factor and the replacement number (Peitgen,
Animated Discussion, 1992).
The jaggedness of the British coastline can be through
of as a fractal dimension. When using the definition for
dimension stated above, the jaggedness of the British coastline
is represented as 1.58. How can something exist with a 1.58 dimension? A way to think about
this number is that the coastline takes up more space than a line, but less space than a two-
dimensional figure, like a square (Bedford, 1998, p. 45). If the Norwegian coastline is examined,
it can be seen that its coastline is much more jagged and therefor it has a higher fractal dimension
of 1.7 (Peitgen, Animated Discussion, 1992).
Therefore, the more jagged coastlines have a higher number and the smoother coastlines
will have a lower number. “A fractal curve, a nominally one-dimensional object in a plane which
has two dimensions, has a fractal dimension that lies between 1 and 2. Likewise a fractal could
Figure 6

also have a dimension between 2 and 3 or between 0 and 1 (McGuire, p. 14). For example, if a
fractal surface has a dimension of 2.3 it would mean that it acts like a two-dimensional object
(such as a circle) but it is defined in a three-dimensional space. Consequently, fractal dimensions
such as these “are important because they can be defined in connection with real-world data, and
they can be measured approximately by means of experiments” (Barnsley, 1988, p. 172). What
are some factors than can alter or affect the fractal dimension? When using Mandelbrot’s ruler
method, something that will ultimately affect the dimensional result is the starting point which
one begins to measure the boundary (Landini, 2010, p. 6-7).
The Cantor Set
Now that the concepts of iteration, recursion, self-similarity, and fractal dimension have been
examined in depth, they will be examined against three famous fractals: the Cantor Set, the Koch
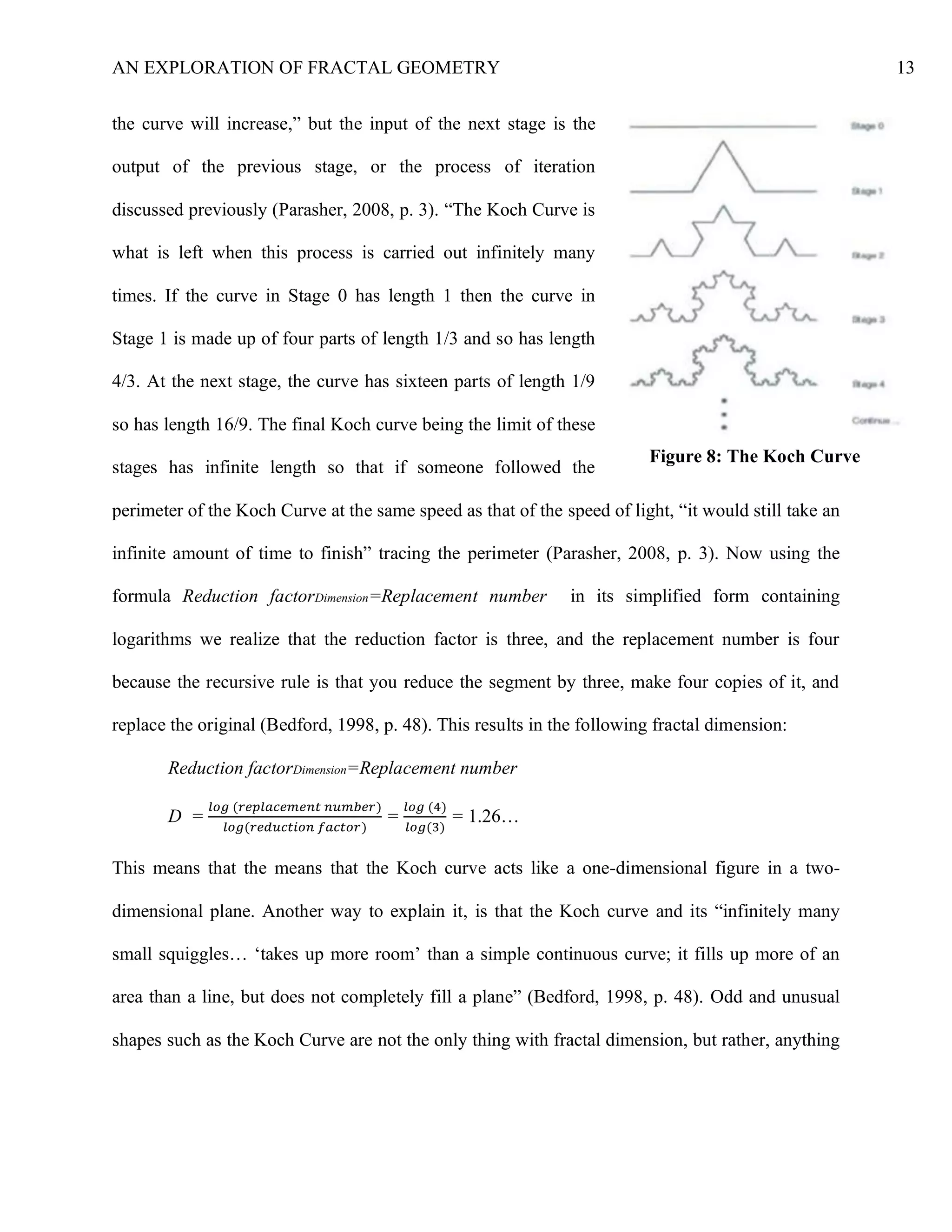
Curve, and the Julia Set. Firstly, the Cantor Set as seen in Figure 7 will be analyzed (Bedford,
1998, p. 47). The German mathematician Georg Cantor (1845-1918) contributed to mathematics
proving that irrational numbers are useful and have a
“logical place” in mathematics, and he is also one of the
main contributors of set theory (Lauwerier, 1991, p. 15).
As seen in Figure 7, the Cantor sets initial stage begins
with a line segment with a length of one, or representing
the interval [0, 1]. In Stage 1, one must “remove the middle third from [0, 1], but not the
numbers 1/3 and 2/3,” so what remains in Stage 1 are “two intervals [0, 1/3] and [2/3, 1] of
length 1/3 each” (Peitgen, Part One, 1992, p. 80). If you do this same process again, you are left
with the union of “four intervals: [0, 1/9] U [2/9, 1/3] U [2/3, 7/9] U [8/9, 1]” as seen in Stage 2
of Figure 7 (Bedford, 1998, p. 46). As you can see from Figure 7, after each iteration the
Figure 7: The Cantor Set

intervals become increasingly smaller, but how small are they actually? The answer to that is
they are “infinitely small” (Bedford, 1998, p. 46). In the Cantor Set, recursion is displayed
through a replacement rule which states that, at every stage of iteration, the output of the
previous stage is reduced by a factor of 3 and replaced “with two copies of the reduction” which
means that the reduction factor is 3 and the replacement number is 2 (Bedford, 1998, p. 47). This
results in the following fractal dimension:
D =
=
𝑙𝑜𝑔 (3)
𝑙𝑜𝑔(2)
= 0.6309…
This means that the dimension of the fractal lies between 0 and 1 so that it takes up more space
than a point but less space than a line (Bedford, 1998, p. 47). As the Cantor set is iterated, what
are left are discrete points, and a fractal that is made up of these discrete, or individual, points is
called “dust,” so in this case it would be called “Cantor dust” (Lauwerier, 1991, p. 16). The
concept of dust will be important when examining the Julia and Mandelbrot sets later on.
The Koch Curve
In order to further analyze all the principles displayed by fractals, the stages of the well-
known Koch Curve fractal, as displayed in Figure 8, will be analyzed (Parasher, 2008, p. 3). The
Koch Curve was actually named after the Swedish mathematician Helge von Koch who
“published an article in which he introduced the curve now named for him” in 1904, and he is
interesting because most of his work had nothing to do with his work with the Koch Curve
(Bedford, 1998, p. 47). The initial stage begins with a line segment. After this, each line segment
is being replaced by four line segments as shown in Stage 1 (Parasher, 2008, p. 3). This is our
recursive process: for “each stage after that, each line segment is replaced by four line segments”
as shown in Stage 1 (Parasher, 2008, p. 3). Therefore, “as the stages progress, the complexity of

the curve will increase,” but the input of the next stage is the
output of the previous stage, or the process of iteration
discussed previously (Parasher, 2008, p. 3). “The Koch Curve is
what is left when this process is carried out infinitely many
times. If the curve in Stage 0 has length 1 then the curve in
Stage 1 is made up of four parts of length 1/3 and so has length
4/3. At the next stage, the curve has sixteen parts of length 1/9
so has length 16/9. The final Koch curve being the limit of these
stages has infinite length so that if someone followed the
perimeter of the Koch Curve at the same speed as that of the speed of light, “it would still take an
infinite amount of time to finish” tracing the perimeter (Parasher, 2008, p. 3). Now using the
formula Reduction factorDimension=Replacement number in its simplified form containing
logarithms we realize that the reduction factor is three, and the replacement number is four
because the recursive rule is that you reduce the segment by three, make four copies of it, and
replace the original (Bedford, 1998, p. 48). This results in the following fractal dimension:
D =
=
𝑙𝑜𝑔 (4)
𝑙𝑜𝑔(3)
= 1.26…
This means that the means that the Koch curve acts like a one-dimensional figure in a two-
dimensional plane. Another way to explain it, is that the Koch curve and its “infinitely many
small squiggles… ‘takes up more room’ than a simple continuous curve; it fills up more of an
area than a line, but does not completely fill a plane” (Bedford, 1998, p. 48). Odd and unusual
shapes such as the Koch Curve are not the only thing with fractal dimension, but rather, anything
Figure 8: The Koch Curve

from the clouds to surface of the ocean during a storm has fractal dimension (Barnsley, 1988, p.
172-173).
Julia Set
Gaston Julia (1893-1978) became a famous mathematician when he published his first
article on iteration of rational functions at the young age of 25 years old (Bedford, 1998, p. 159).
After his time as a professor in France, his work remained pretty much forgotten until
Mandelbrot built off of it decades later, and using computers was able to create some of the most
beautiful fractals (Peitgen, Part One, 1992, p.138).
Some of the most intricate and beautiful fractals are defined using complex numbers, or a
combination of real and imaginary numbers, and “Julia sets live in the complex plane” (Peitgen,
Part One, 1992, p. 139). One must understand that both real and
imaginary numbers are “just as real and just as imaginary as any
other sort” of numbers, and that complex numbers, being a
combination of the two, can be manipulated under mathematical
operations of addition, subtraction, etc. and “just about any
calculation on real numbers can be tried on complex numbers as
well” (Gleick, 1987, p.216). To review, the common notation
for complex numbers is written as z=x+iy representing “x as a
variable along the real axis, y as a variable along the imaginary axis and z as the complex
variable, that is, the variable position in the plane” and i=√−1 as seen in Figure 9 (McGuire,
1991, p. 74). “A Julia Set is a set of points on the complex plain that is defined through a
process of function iteration” (Bedford, 1998, p. 159). More specifically, a Julia set can be
Figure 9

defined by a conformal transformation, or “a transformation that leaves angles unchanged”,
which is also iterative, and an example of this is below (Lauwerier, 1991, p. 124).
x’=x2-y2+a
y’=2xy+b
For example, take the polynomial x2+c where c is some arbitrary, fixed position in the complex
plane, and, in order to iterate it, we “choose some value for x and obtain x2+c ” and “substitute
this value for x and evaluate” the original polynomial x2+c over and over again, infinitely many
times (Peitgen, Part One, 1992, p. 139). The result is “a sequence of complex numbers” as seen
below:
x → x2+c → (x2+c)2+c → ((x2+c)2+c)2+c → … (Peitgen, Part One, 1992, p. 141).
When the polynomial sequence of complex numbers x2+c is iterating continuously, as seen
above, the sequence has to meet at least one of the two properties: “either the sequence becomes
unbounded,” that is the elements in the sequence leave a circle around the origin,” or “the
sequences remains bounded” meaning that a circle around the origin exists so that the sequence
never leaves it” (Peitgen, Part One, 1992, p. 141).
Now, taking a step away from complex number and examining only the real numbers, in
order to define the key concept of an attractor. “The figure that arise from iterating linear
transformations are said to be the attractors of the iteration,” and “a really simple example of
attraction is what happens when a number on the real line is iteratively squared; that is xnew =
x2old (McGuire, 1991, p. 74).. If we begin by letting xold=0.9, then the following results from the
formula above (x2old = xnew):

0.9 x 0.9 = 0.81
0.81 x 0.81 = 0.6561
0.6561 x 0.6561 = 0.43046…
…and after ten iterations = 1.39 x10-47
Because of iteration, the value 0.81 now becomes xold, and the process is repeated continuously,
and after each stage the values of xnew become smaller and smaller and therefore, the attractor
point is zero (McGuire, 1991, p. 74). Similarly, if we begin by letting xold= 1.1, then the
following results from the formula above (x2old = xnew):
1.1 x 1.1 = 1.21
1.21 x 1.21 = 1.4641
1.4641x 1.4641= 2.14358…
…and after ten iterations = 2.43 x1042
Because of iteration, the value 1.21 now becomes xold, and the process is repeated continuously,
and after each stage, the values of xnew become larger and larger and therefore, the attractor point
is infinity (McGuire, 1991, p. 74). These examples allow Julia points to be defined.
If there is function with a domain that is complex and it “has an attracting fixed point or
cycle, then the points that approach the attractor as a limit are called Prisoner Points” (Bedford,
1998, p. 162). The set of all these points is called the prisoner set and are shaded in black in
Figure 10 on the following page, and it can be illustrated in the previous example where xold= 0.9
and the attractor was zero. Those points whose orbits under the function “tend to infinity are
called Escaping Points” (Bedford, 1998, p. 162). The set of all these points is called the escaping
set and are shaded in black in Figure 10, and it can be illustrated in the previous example where
xold= 1.1 and the attractor was infinity. Then there are the remaining points called Julia Points

and are shaded in black in Figure 10. These points “do not tend to an attracting fixed point or
cycle and which do not tent to infinity,” and
“the set of all Julia Points is called the Julia
Set” (Bedford, 1998, p. 162).
How can Julia points be illustrated using
our previous formula x2old = xnew ? If we let xold=1.0 then the function would appear to be fixed at
the value of 1, but the function is actually very unstable. This is because if you take the tiniest
number you can think of and subtract it from 1 to equal xold, the attractor is zero, resulting in a
prisoner point (McGuire, 1991, p. 75). Conversely, if you take the most minute number you can
think of and add it to 1 to equal xold, the attractor is becomes infinity, resulting in an escaping
point.
To explore the meaning behind this phenomenon, the same function will be used under
the complex number plane written as a function of z, where z is some complex number. Keeping
these properties in mind, the sequence can be applied in the complex plane and acts similarly,
using the form mentioned earlier and use a simple transformation of z where znew=z2old .
Therefore, if zold=0.9, the points in Figure 10 show that the attractor is zero and it results in the
prisoner set. If zold=1.1, the points in Figure 10 show that the attractor is infinity and it results in
the escaping set. . If zold=1.0 the points in Figure 10 show that there is no attractor and it is
unstable, jumping around on the circle z=|1| and it results in the Julia set.
Now, a complex constant will be added to the equation on the complex plane resulting in
znew=z2old+c where c is some constant position on the complex plane. It could be written as
z=(x+iy)2 +a+ib, and c= a+bi where c is a constant position on the complex plane (McGuire,
1991, p. 74). Unlike Figure 10, this results in a set of Julia points that is not a circle, except for
Figure 10

the trivial case when c is equal to zero (McGuire, 1991, p. 75). The boundary, called the Julia set,
is a fractal which depends on the value of the complex constant c
(McGuire, 1991, p. 75).
These different values of c produce different Julia sets.
However, all of these Julia sets have common characteristics being
that they are all dependent on the value of c, they all fall within the
|z|=2, and they are all symmetric about the origin of the complex
plane (McGuire, 1991, p. 75). Now, look at the two Julia sets in
Figure 11 illustrated by the formula znew=z2old+c (numerous stages
can also be seen in Appendix A for different values of c). The
white part in Figure 11 represents those points that are attracted to
infinity, or the escaping points, and the black part are those that are
not attracted to infinity (McGuire, 1991, p. 75). These are both the
prisoner points as well as the Julia points, but the boundary of the black part is the Julia points.
Displayed in Figure 12 are different Julia Sets displayed by the iteration znew=z2old+c
where c is some constant position on the complex plane (Strzyzewski, 2008). These have the
initial conditions that z=x+iy, c=a+ib, -4<x<4, -3<y<3, and -16<b<16, and the
green lines in Figure 12 represent the complex coordinate plane. As in Figure
11, the Julia set in Figure 12 and all Julia sets are
mapped onto the complex plain using “a grid of points
in the square region bounded by -2 and 2 on the real axis and -2i and 2i on
the imaginary axis (McGuire, 1991, p. 77). This creates “a contour map
whose ‘elevations’ are the number of iterations” where the different colors
Figure 11: Julia sets
Figure 12.2
Figure 12.1

are used to keep count of the number of iterations of z for each point up to some maximum
number as long it stays within |z| = 2 (McGuire, 1991, p. 77).
Recall discussing the Cantor Set as “Cantor dust,” and also recall the fact that when a
fractal is made up of these discrete, or individual, points it is called “dust” (Lauwerier, 1991, p.
16). The Julia set in Figure 11 where c=0.354+0.5361i can satisfy
the “dust” condition (McGuire, 1991, p. 76). Therefore some Julia
sets that can be described as “Julia dust,” but “for what values of c
do Julia sets have a connected substance?” (McGuire, 1991, p. 78).
Mandelbrot posed this question, and his solution was “an incredible
organizing principle” which results in the fractal figure in Figure 13,
and this fractal known as the Mandelbrot set “is the part of the complex plane where the c values
have Julia sets which are not dusts” (McGuire, 1991, p. 78-79). A larger and more detailed
picture of the connected Julia sets within the Mandelbrot can be seen in Appendix B.
Fractals in Biology
How then are fractals used and studied in other fields of science? Fractals have had a
significant impact in the study of microscopy, which is the biological study of things using a
microscope, and also morphology, which is a “branch of biology that deals with the form and
structure of animals and plants” or “the form and structure of an organism or any of its parts”
(Merriam-Webster Online). Since Mandelbrot’s development of fractal geometry and his
research on properties such as iteration, recursion, self-similarity, and fractal dimension, the
study of fractal geometry has had an immense impact on these fields of science. “Fractals have
profound implications in relation to the effects of magnification and scaling on morphology” and
the measurement methods needed to measure self-similar figures (Landini, 2010, p.1).
Figure 13: Mandelbrot Set

Particularly, the concept of self-similarity has been important in microscopy because
“discrepancies in surface and volume estimation in tissues under varying magnification” which
can be “explained within the framework of fractals” (Landini, 2010, p.3). However, while
fractals in the natural world display self-similarity, there are limits because of the “existence of
discrete structural units” which will not show “the same degree of detail when the observation
scale” increases because they don’t display infinitely small amounts of details like true fractals
(Landini, 2010, p.3). Then why is it common to see fractals appearing in biological structures? It
is partly because of the fractal properties of recursion and iteration. Cells in biological systems
“are often the structural replicating of units that iterate the previous state of tissue or colonies”
(Landini, 2010, p.3). Therefore, because “fractals commonly appear in ‘disordered systems’
controlled by physical phenomena…where randomness is thought to play a role, so it would not
be surprising if similar mechanisms are also at play during morphogenesis, development or
carcinogenesis,” or the generation of cancer cells in living organisms (Landini, 2010, p.3).
In conclusion, fractals are extremely complex geometric figures, and they are all around
us in the natural world. They demonstrate certain properties such as recursion, iteration, self-
similarity, and fractal dimension, and they can appear as simple as the Cantor Set or as complex
as the Julia Set. Because of its use in of theoretical and experimental mathematics, fractal
geometry has also had a major impact in other scientific fields and research. As the main
contributor of fractal geometry Benoit Mandelbrot explains that “fractal geometry is not just a
chapter of mathematics, but one that helps Everyman to see the same old world differently”
(McGuire, 1991, Forward).

References
Barnsley, M. (1988). Fractals Everywhere. United States of America: Academic Press, Inc.
Bedford, C.W. (1998). Introduction to Fractals and Chaos: Mathematics and Meaning.
Andover, MA: Venture Publishing.
(n.d.) Untitled (British Coastline Image). [Photograph]. Retrieved from: https://upload.
wikimedia.org/wikipedia/commons/2/20/Britain-fractal-coastline-combined.jpg.
Gleick, James. (1987). Chaos: Making a New Science. Harrisonburg, VA: R.R. Donnelley &
Sons Co.
Gowers, T. (Ed.) Barrow-Green, J. & Leader, I. (Assoc. eds.). (2008). The Princeton Companion
to Mathematics. Princeton, NJ: Princeton University Press.
Landini, G. (2010). Fractals in microscopy. Journal of Microscopy, 241(1), 1-8.
doi: 10.111/j.1365-2818.2010.03454.x
Lauwerier, H. A. (1991). Fractals: Endlessly Repeated Geometrical Figures. Princeton, NJ:
Princeton University Press.
Mandelbrot, Benoit B. (1977). The Fractal Geometry of Nature. New York: W.H. Freeman and
Company.
McGuire, Michael. (1991). An Eye For Fractals. United States of America: Addison-Wesley
Publishing Co., Inc.
Morphology [Def. 1]. (n.d.). Merriam-Webster Online. In Merriam-Webster. Retrieved
December 13, 2015, from http://www.merriam-webster.com/dictionary/morphology
Parasher, R. (2008). Fractal Dimension: Measuring Infinite Complexity. Pi in The Sky, (12), 3-5.
Peitgen, H.O., Jurgens, H., Saupe, D., Maletsky, E., Perciante, T., & Yunker, L. (1992). Fractals
for the Classroom: Part One Introduction to Fractals and Chaos. Rensselaer, NY:
Springer-Verlag New York, Inc.

Peitgen, H.O., Jurgens, H., Saupe, D., & Zahlten C. (Producers). (1990). Fractals: An Animated
Discussion [VHS]. New York: W.H. Freeman and Company.
Strzyzewski, F. [Florian Strzyżewski]. (2008, May 3). More about Julia Set Fractal - part 1 of 3.
[Video File]. Retreived from: https://www.youtube.com/watch?v=RAgR_KVWtcg&
index=2&list=PLymzxCT1I9d3cmOQgZWwjff6jd0uEW0kk.

Appendix A
Examples of Julia sets for different values of c substituted into znew=z2old+c where c is some
constant position on the complex plane. (Peitgen, Part One, 1992, p. 140).

Appendix B
A larger and more detailed picture of the connected Julia sets within the Mandelbrot Set
(Peitgen, Part One, 1992, p. 318).

An Exploration of Fractal Geometry

More Related Content

Similar to An Exploration of Fractal Geometry

More from M H

Recently uploaded

An Exploration of Fractal Geometry