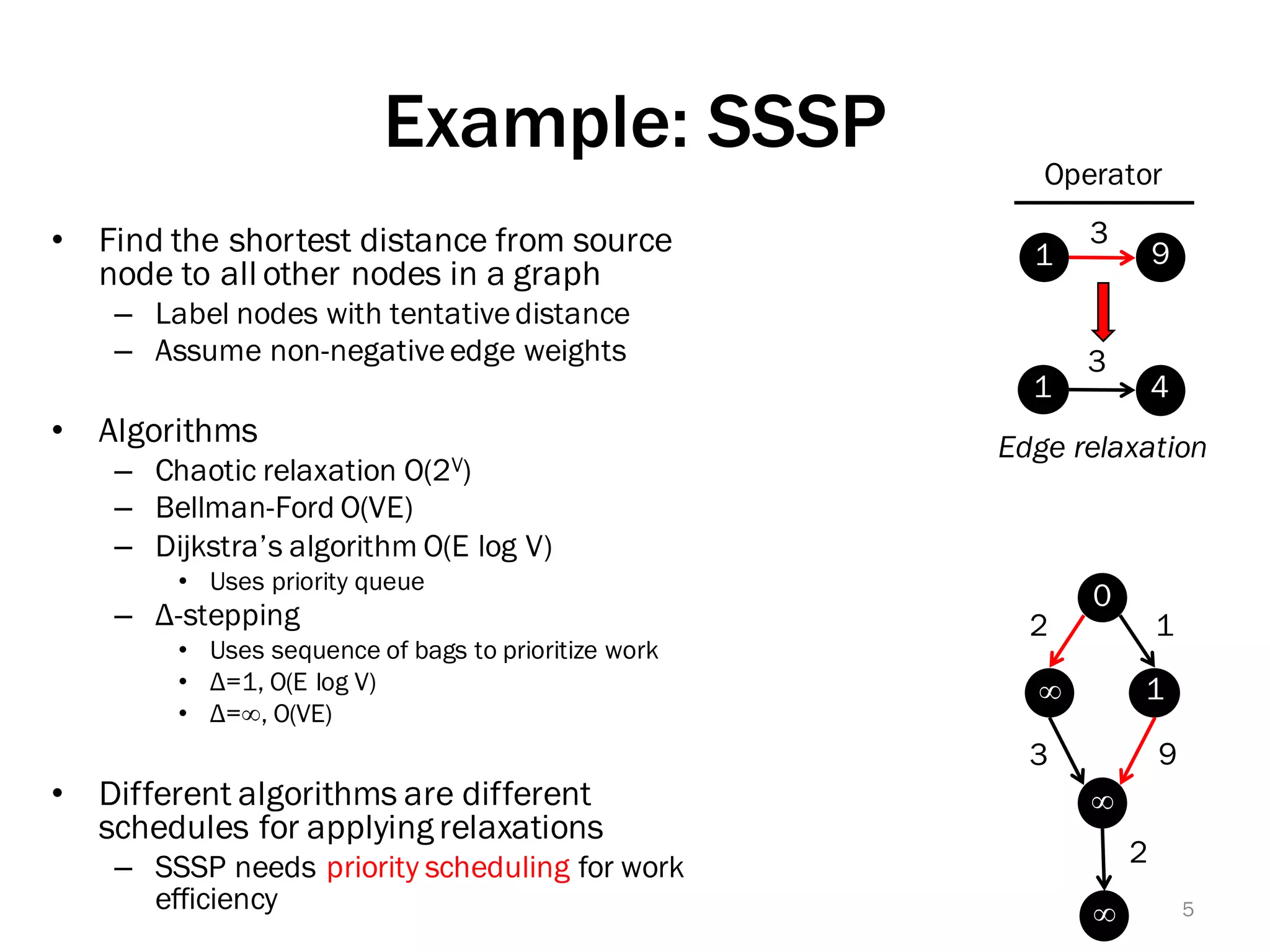
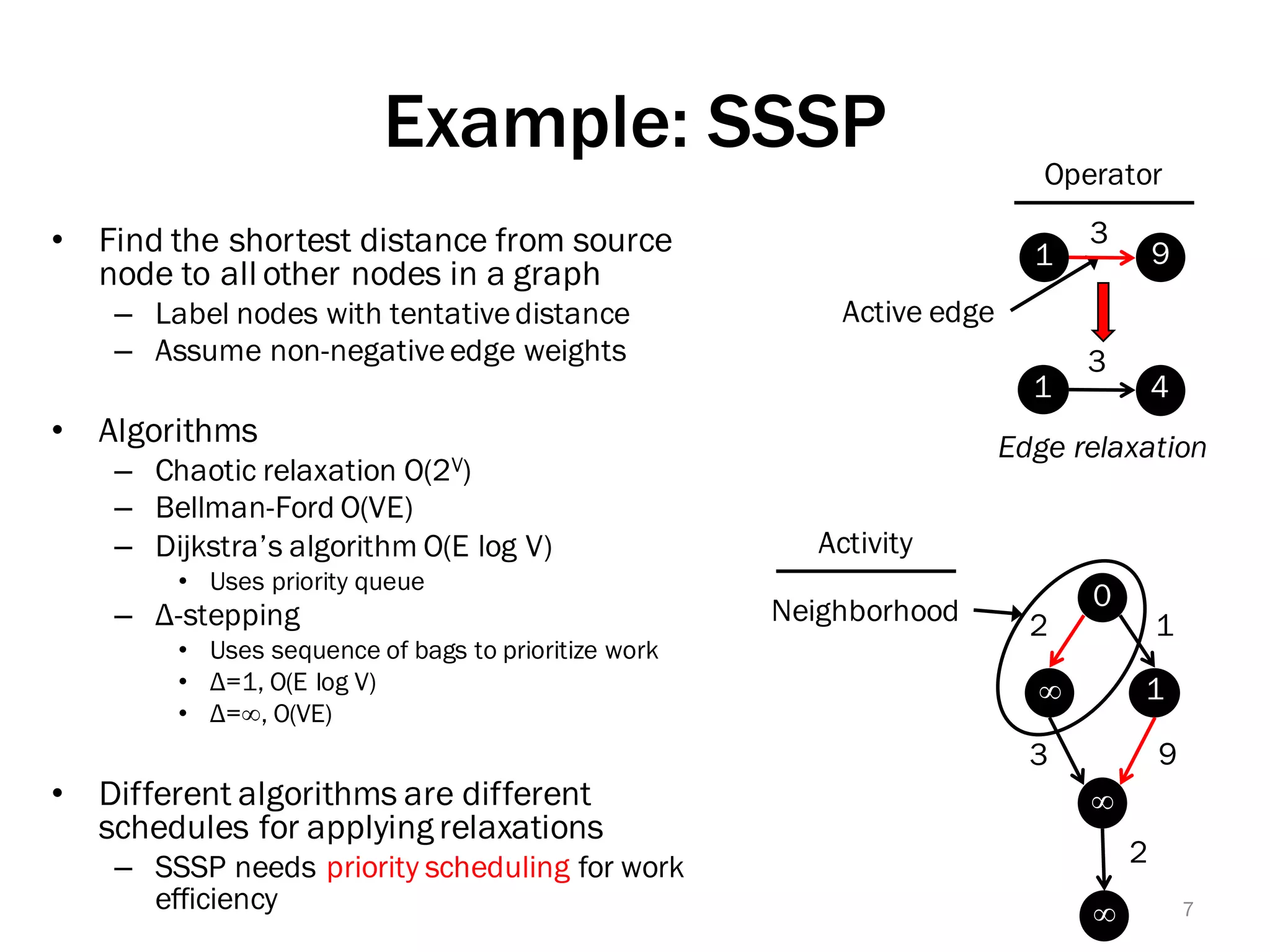
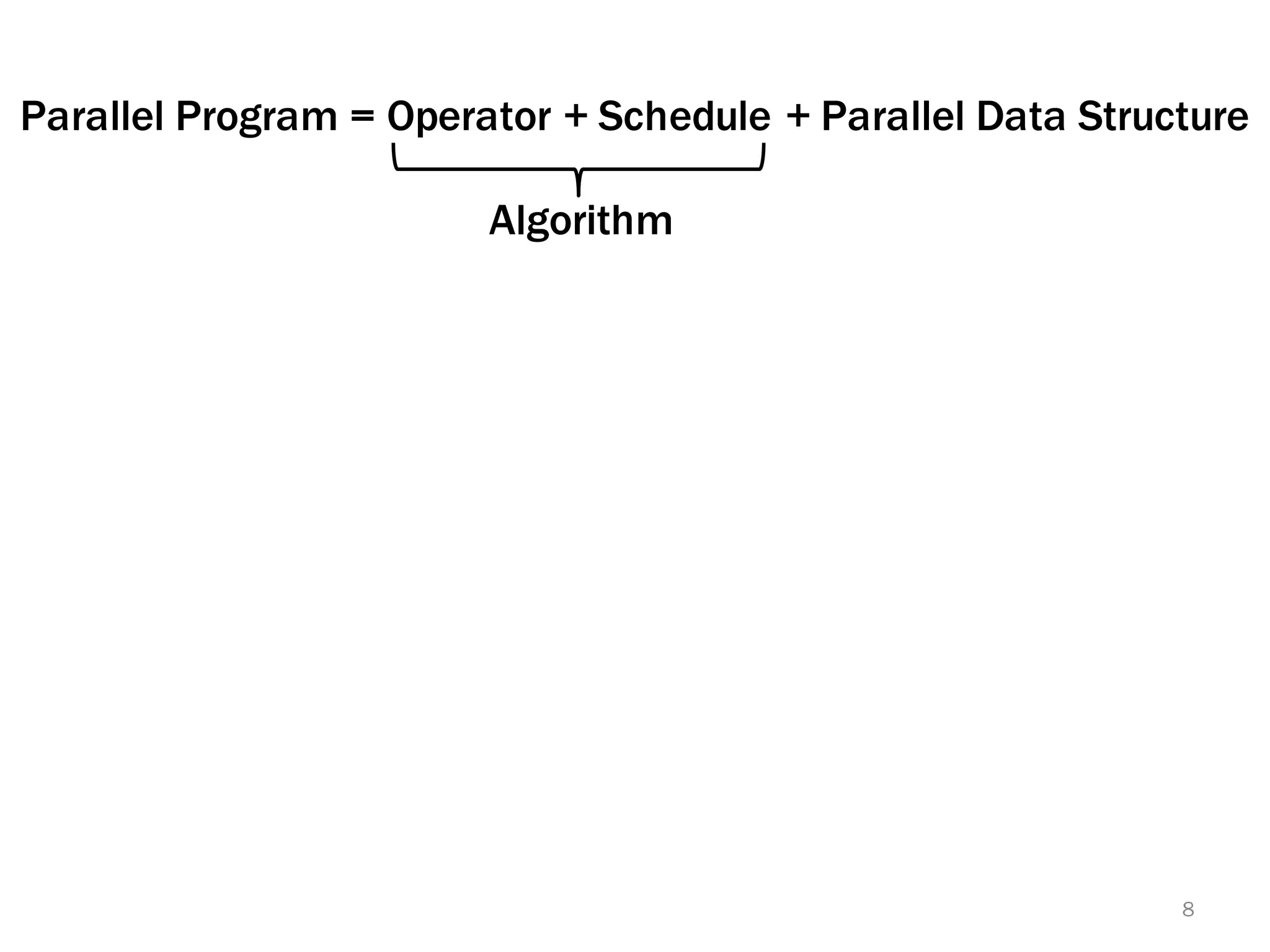
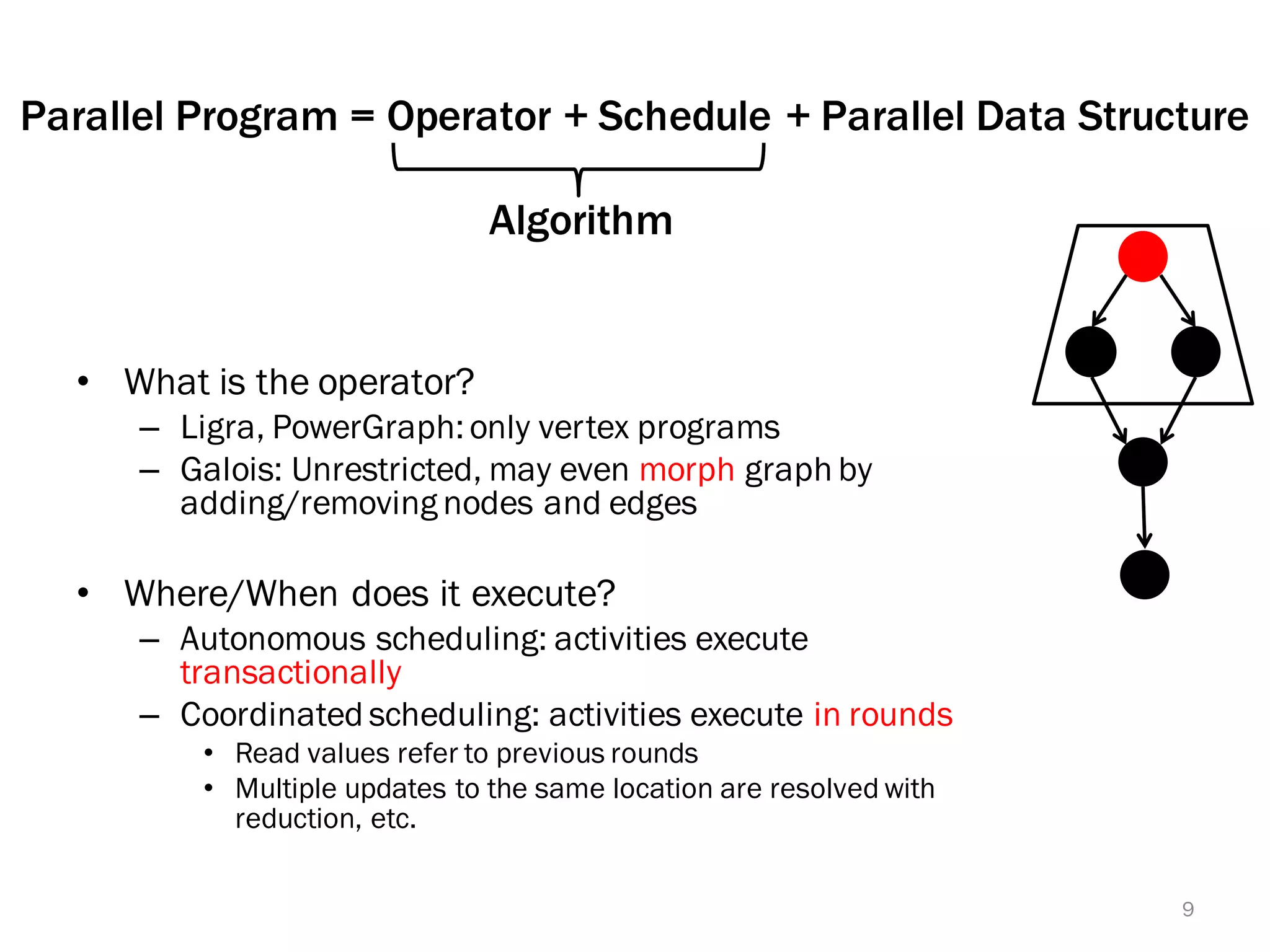
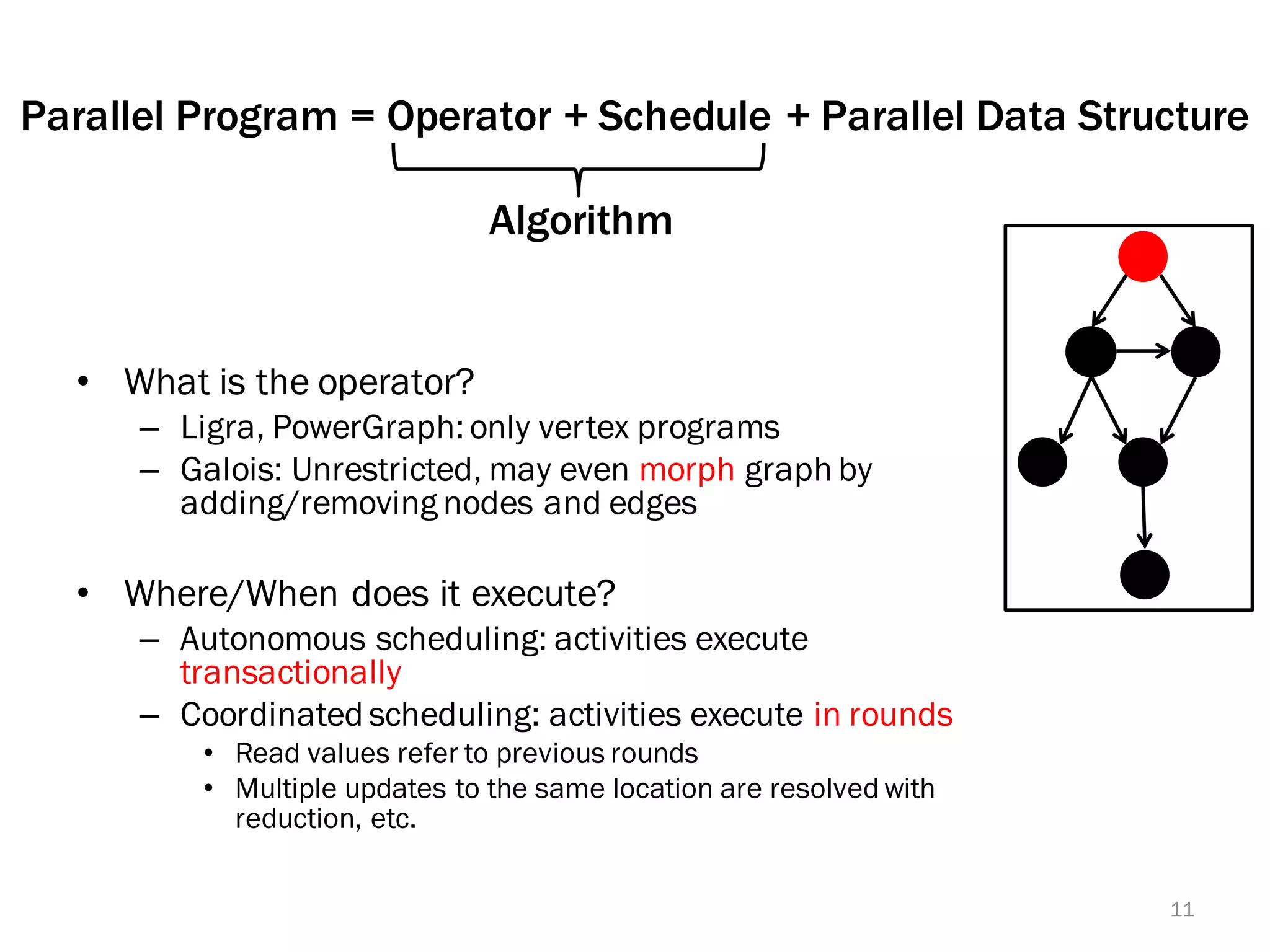
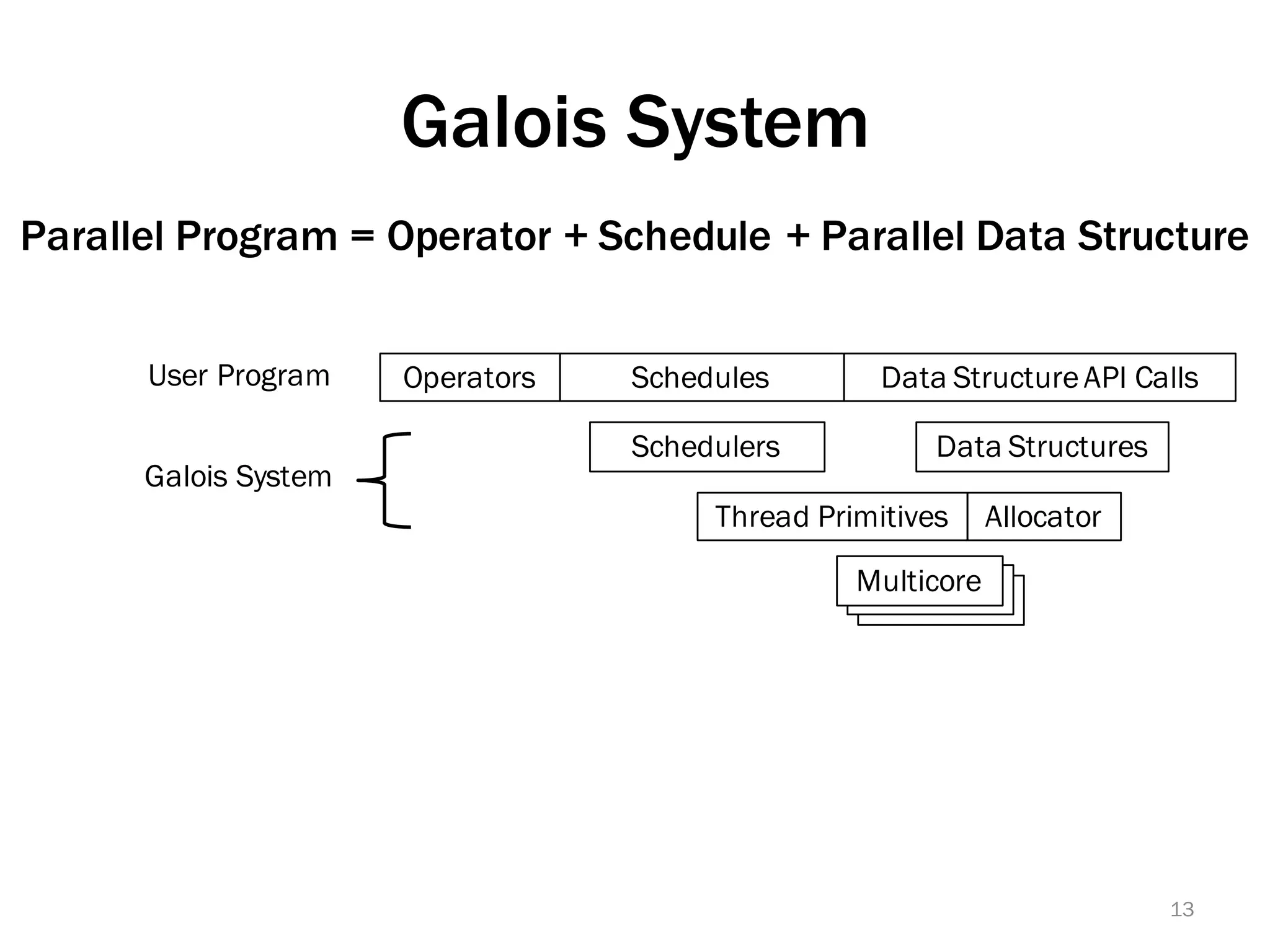
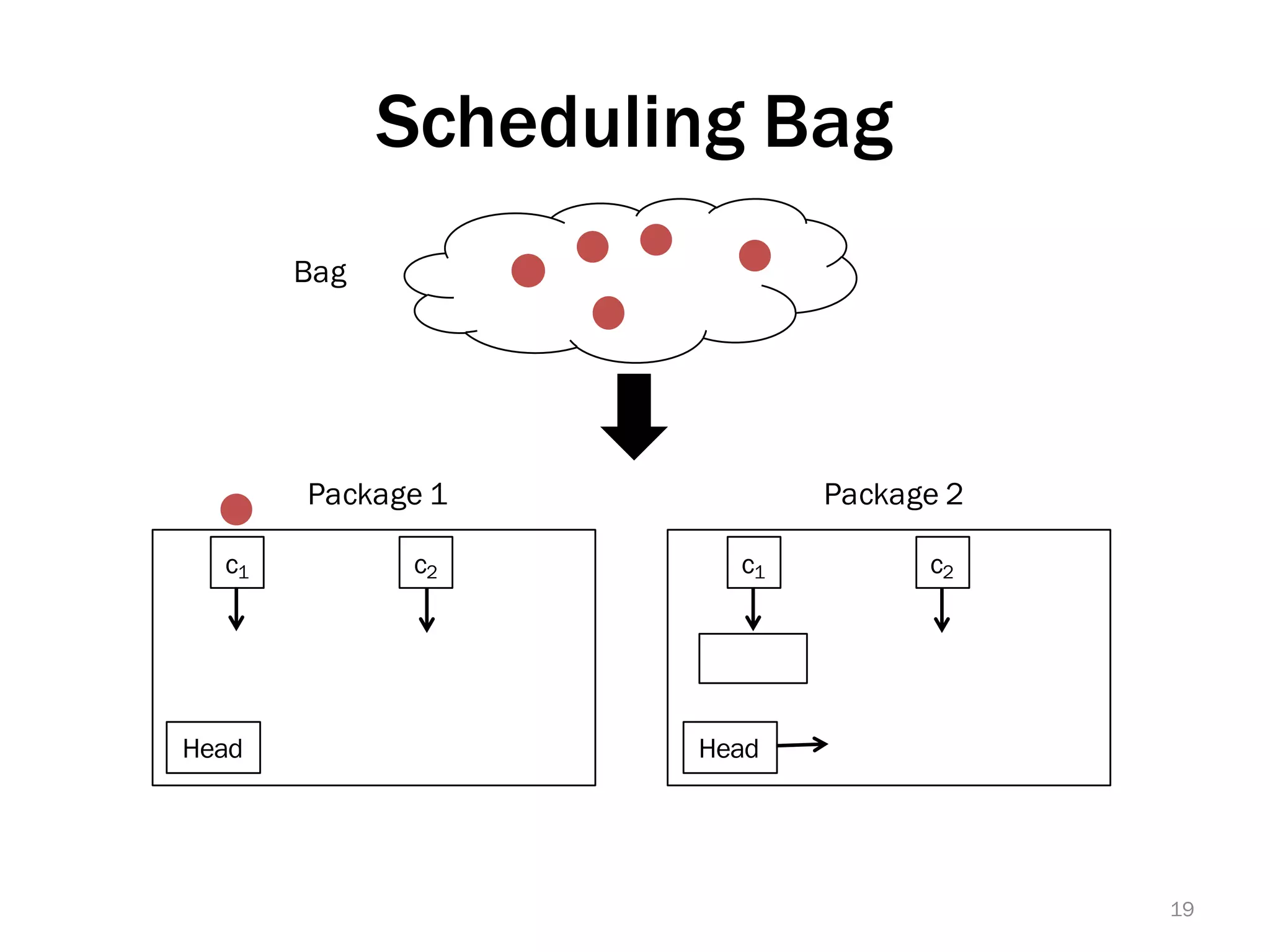
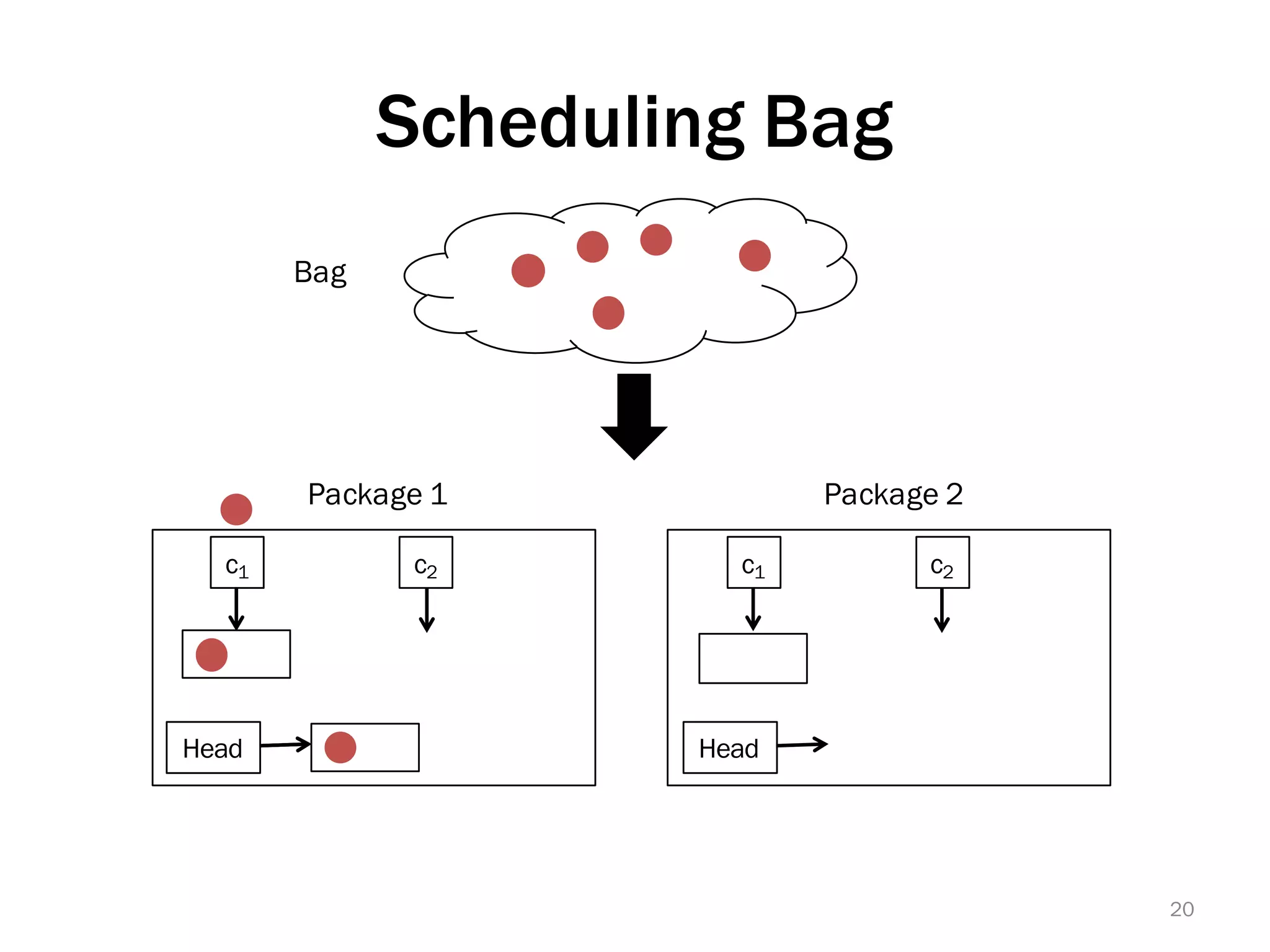
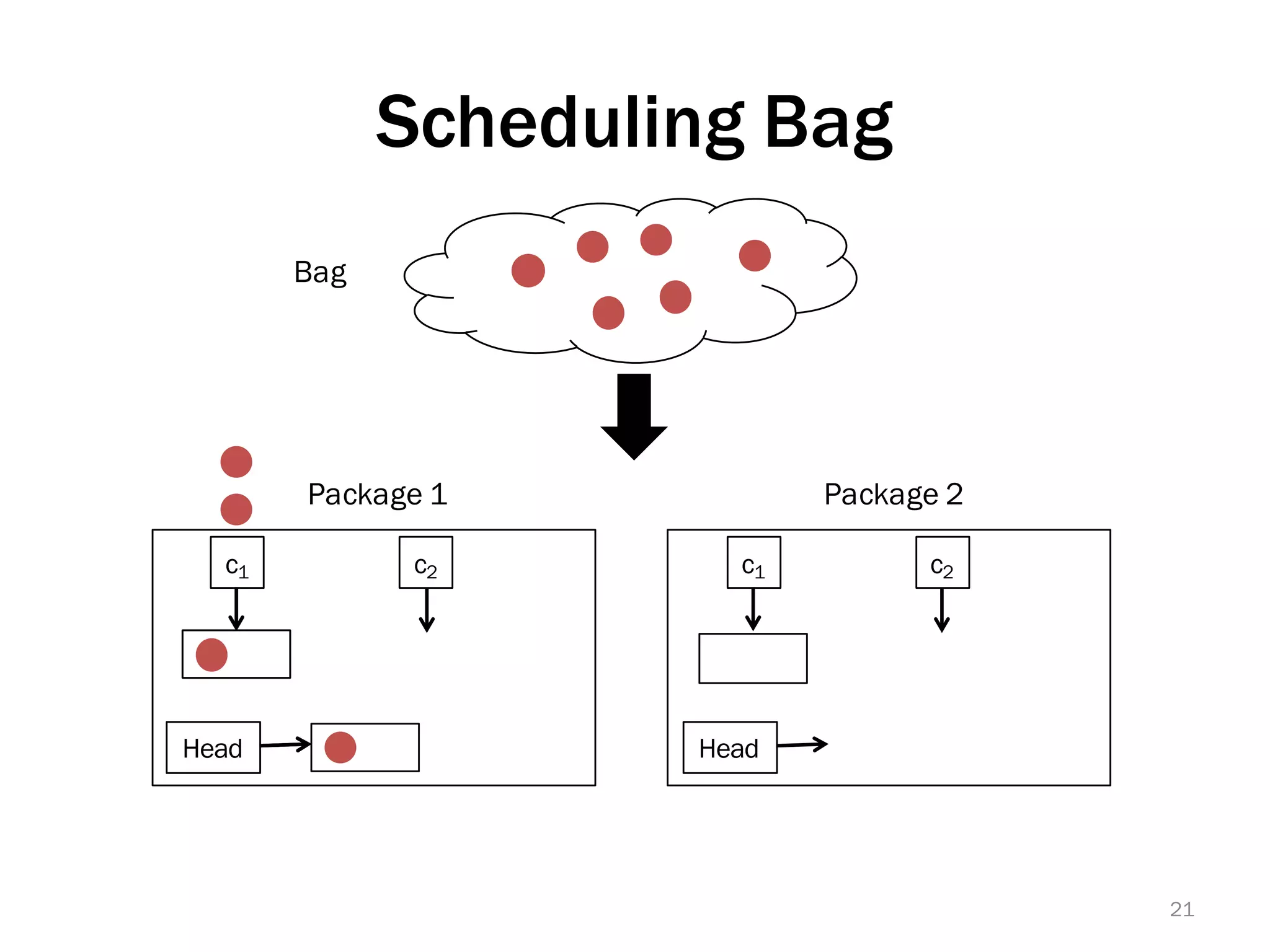
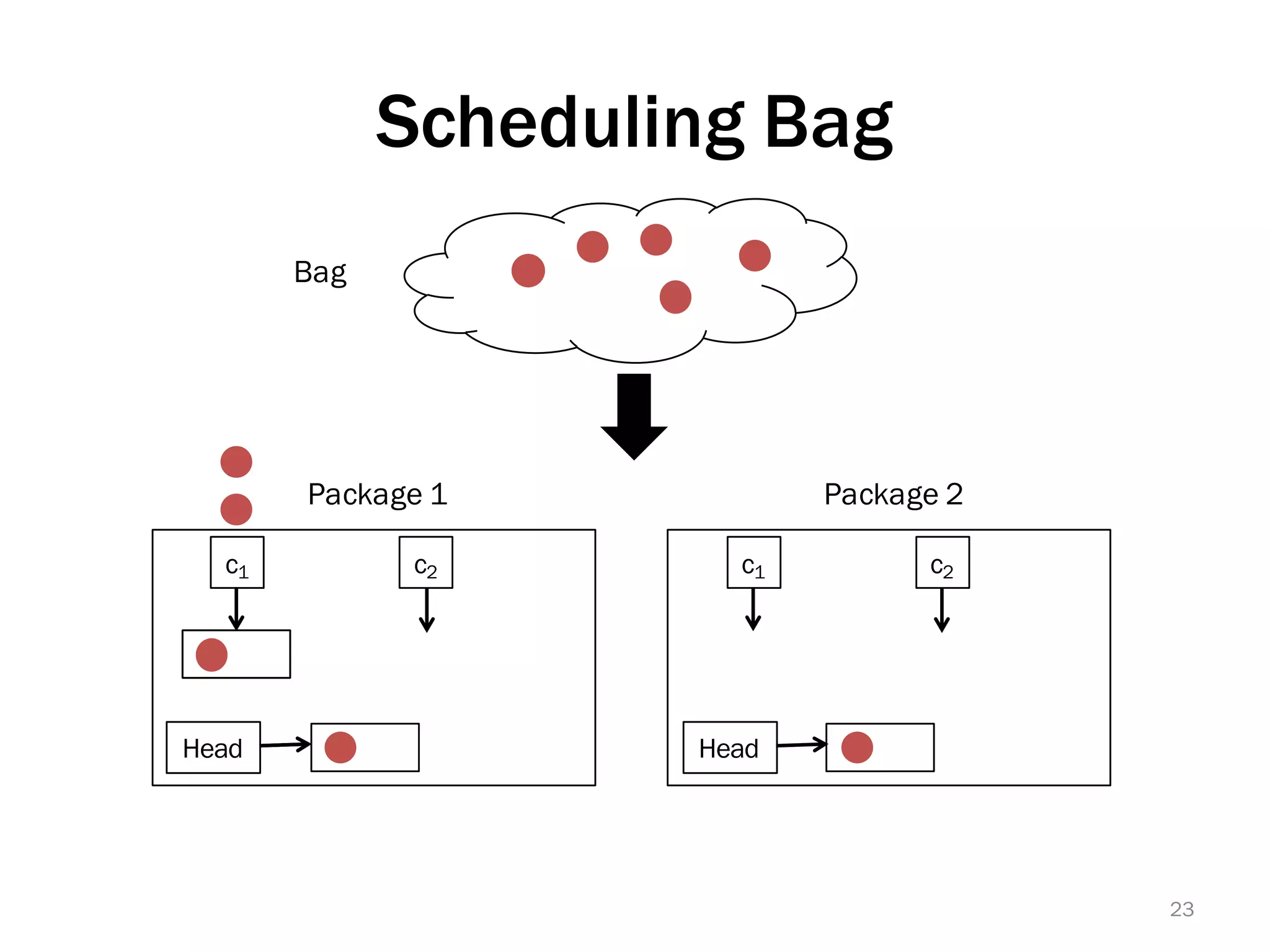
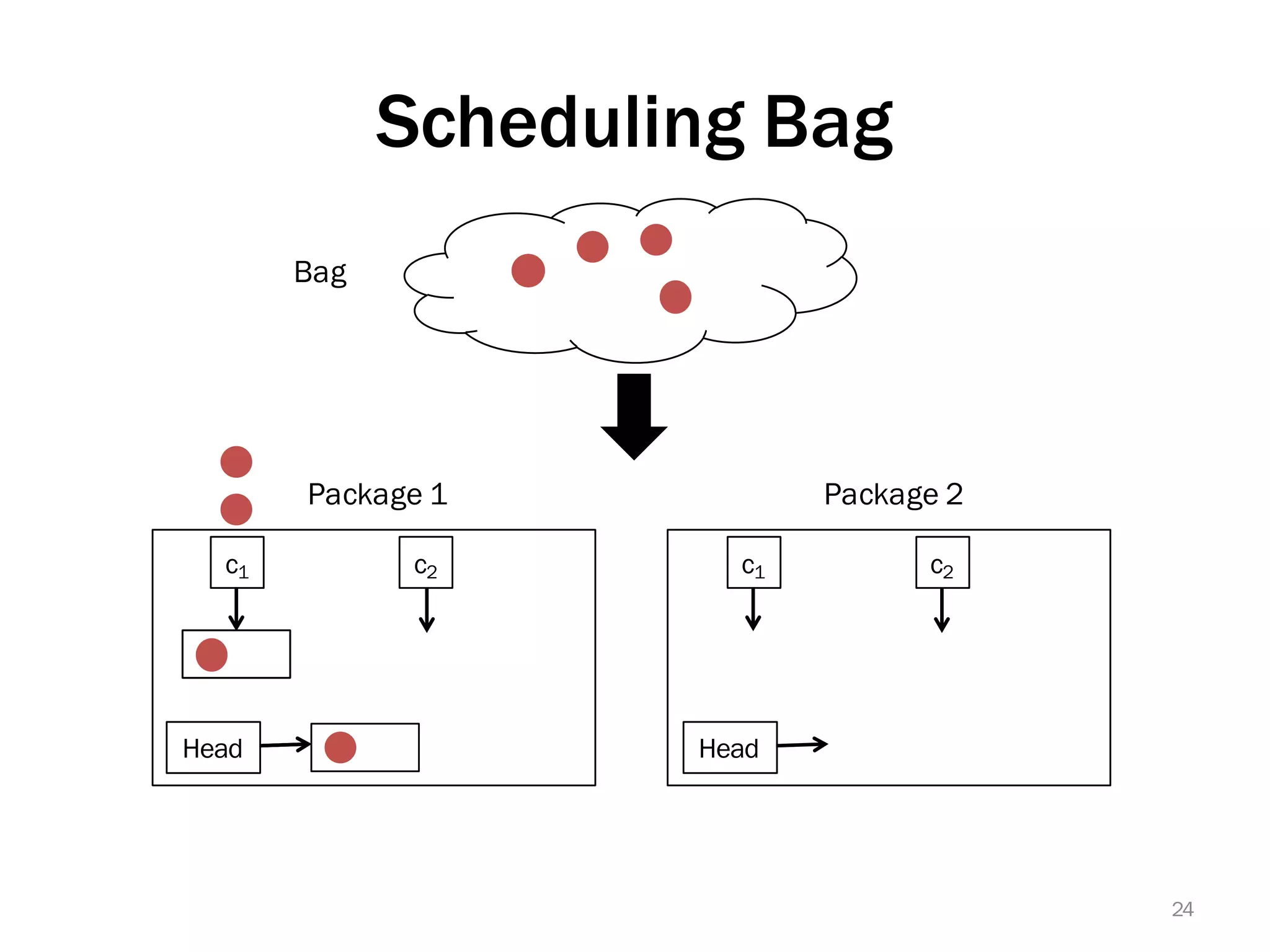
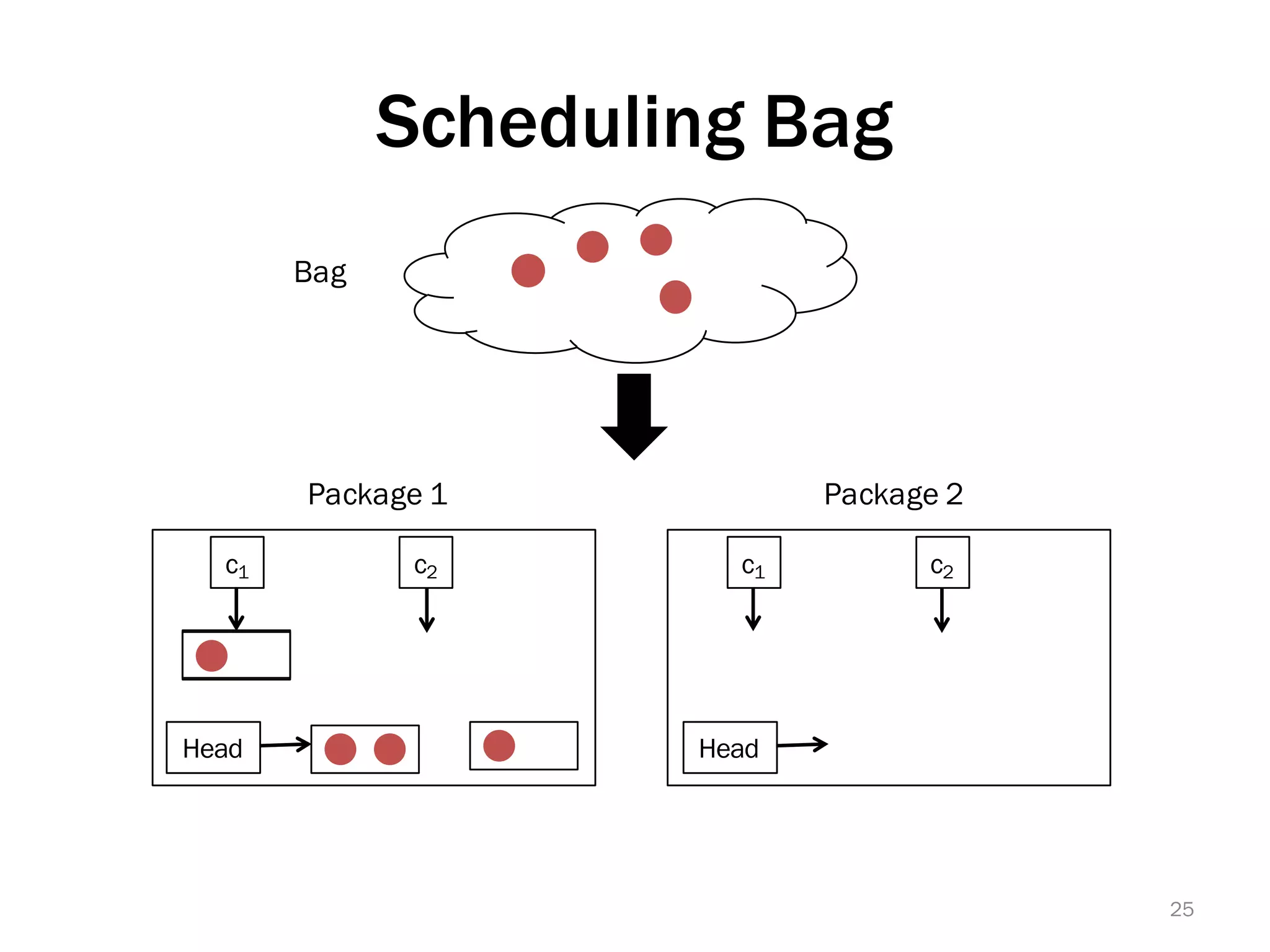
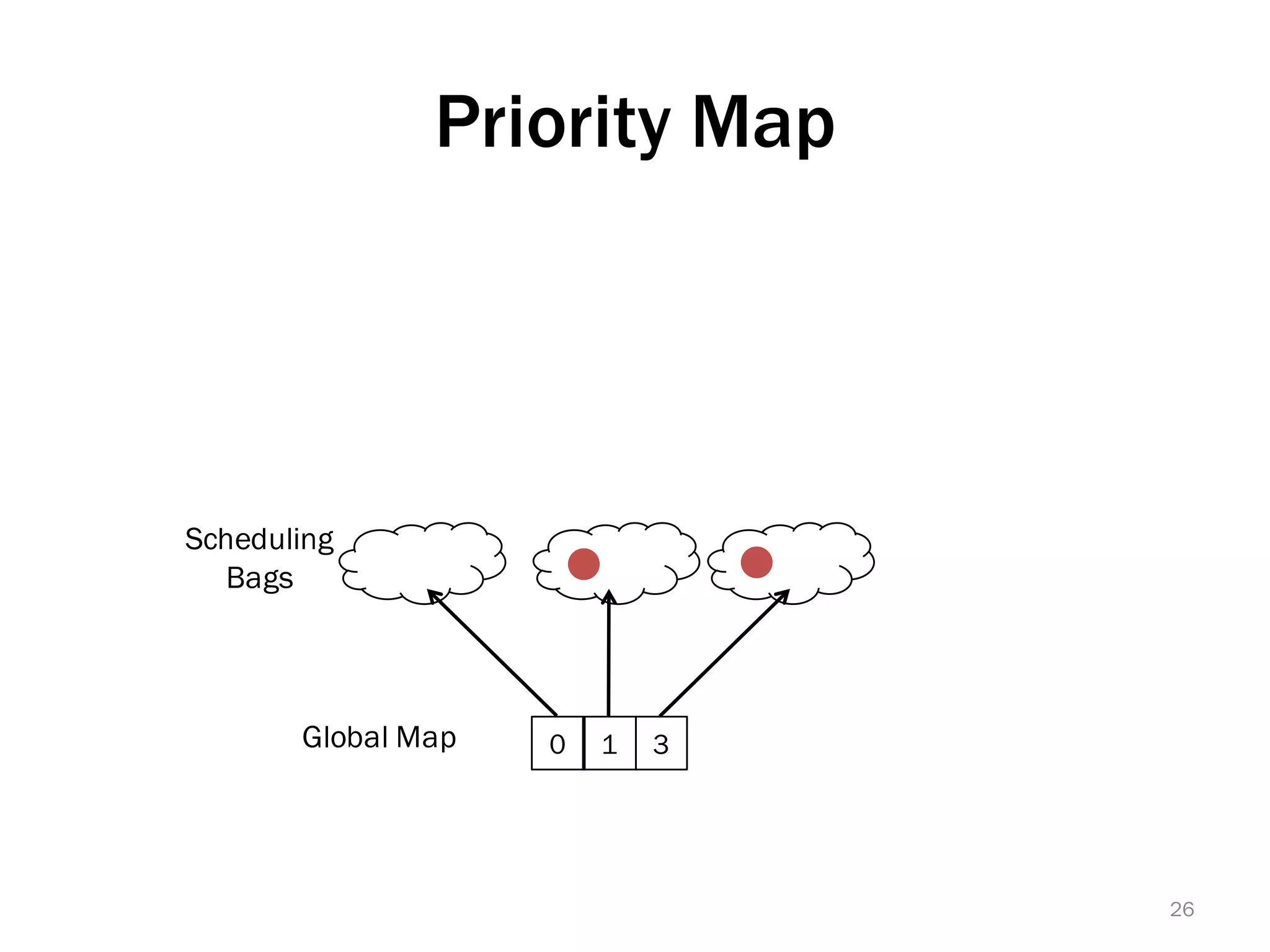
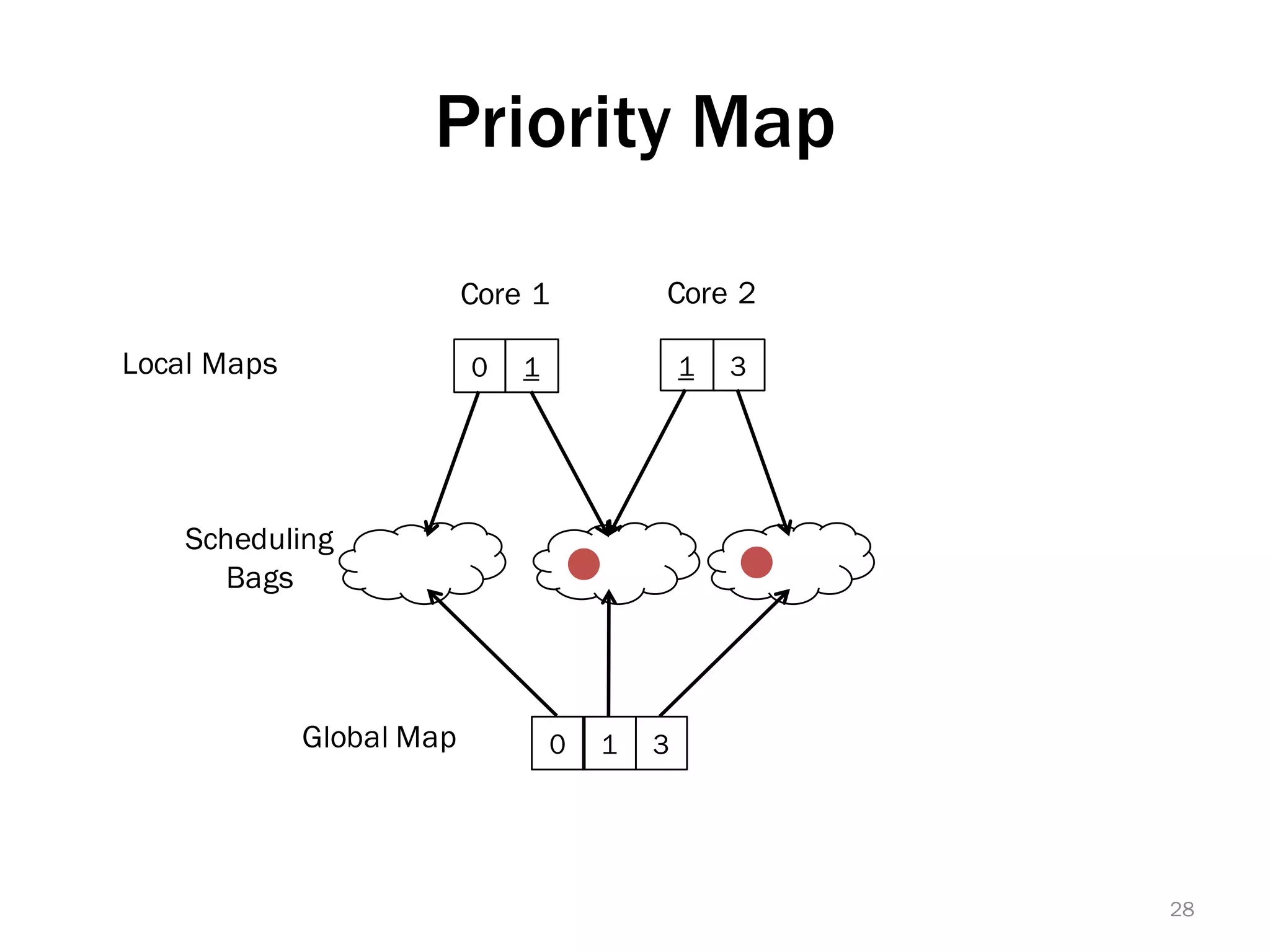
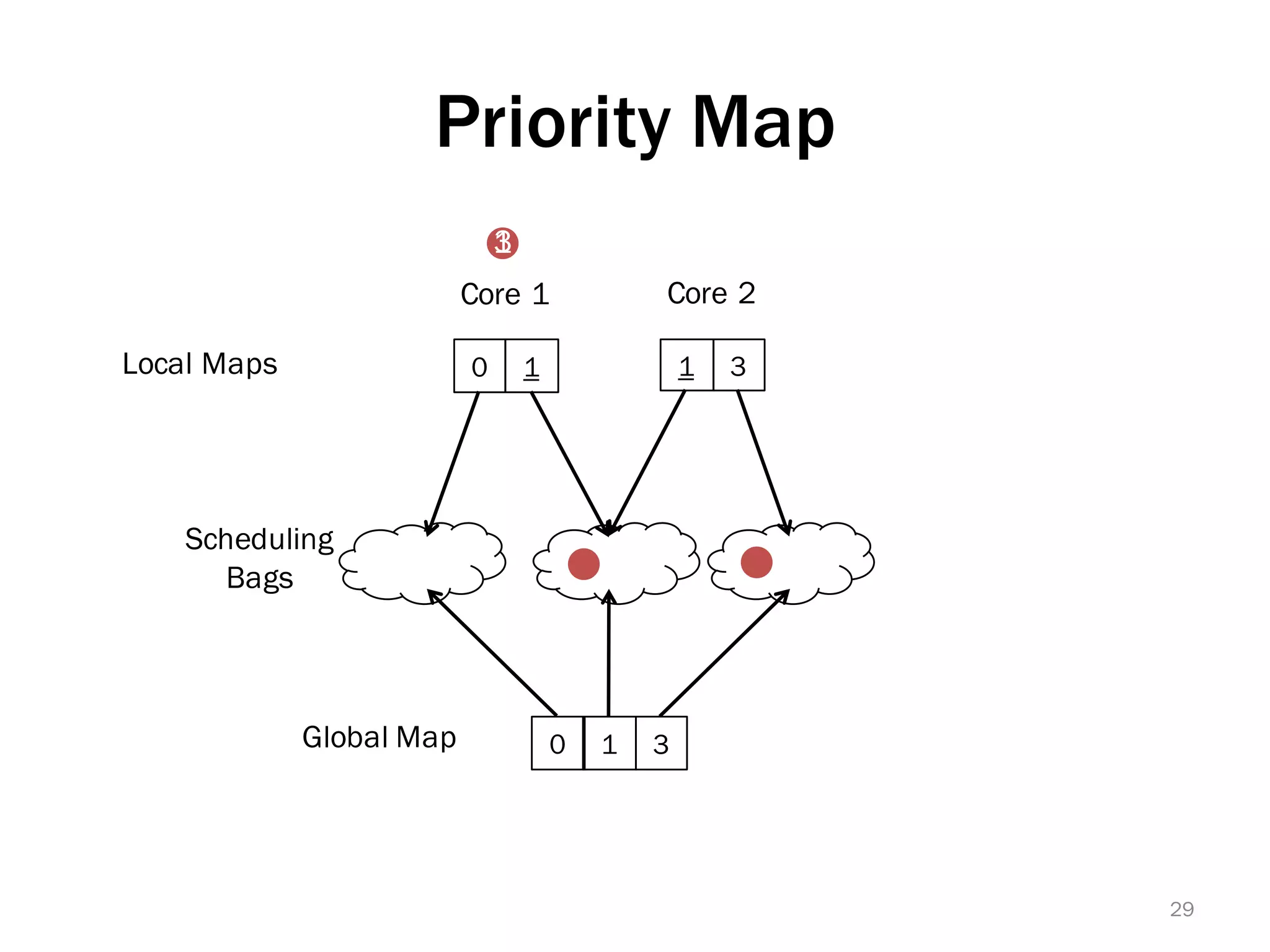
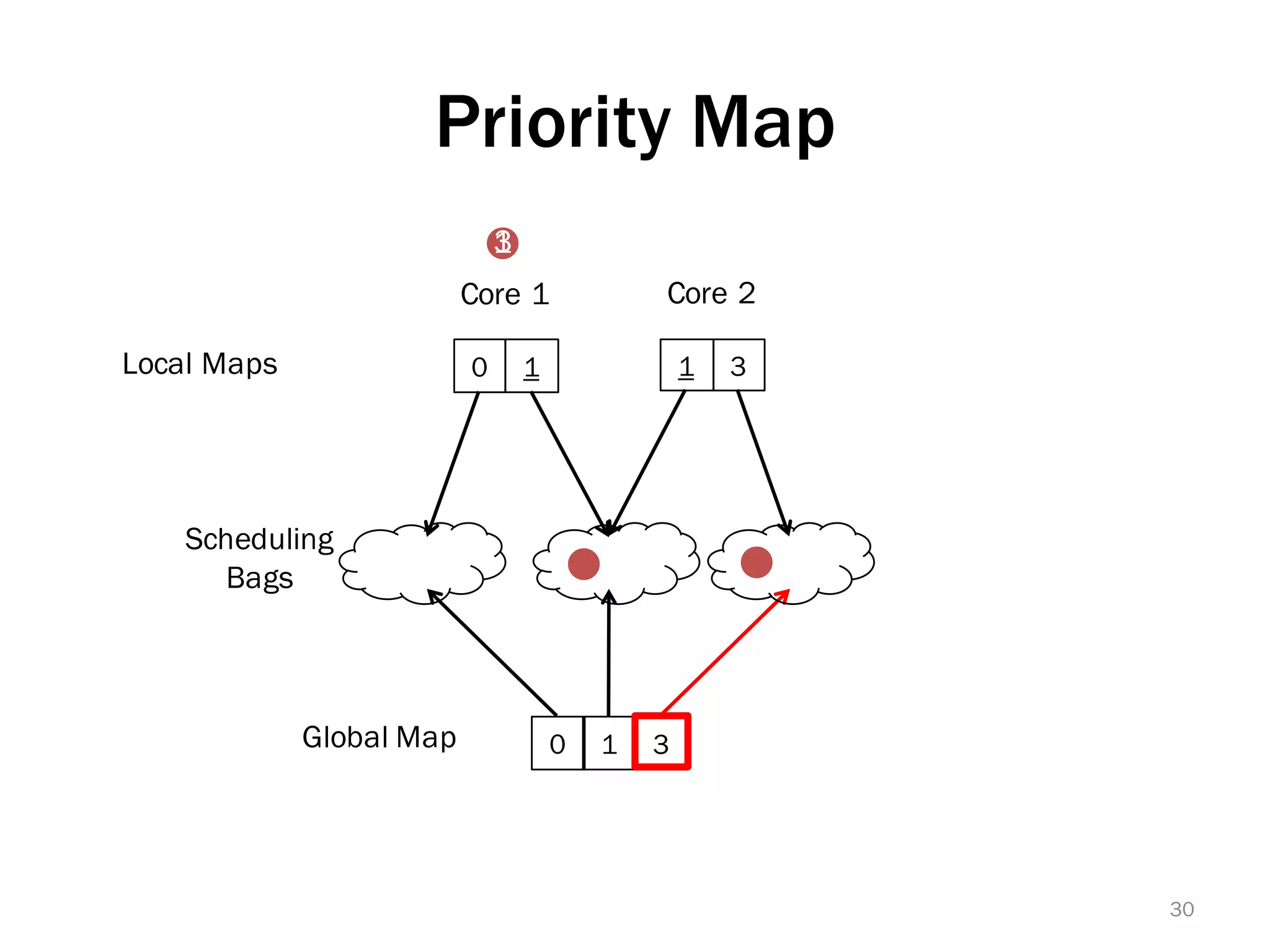
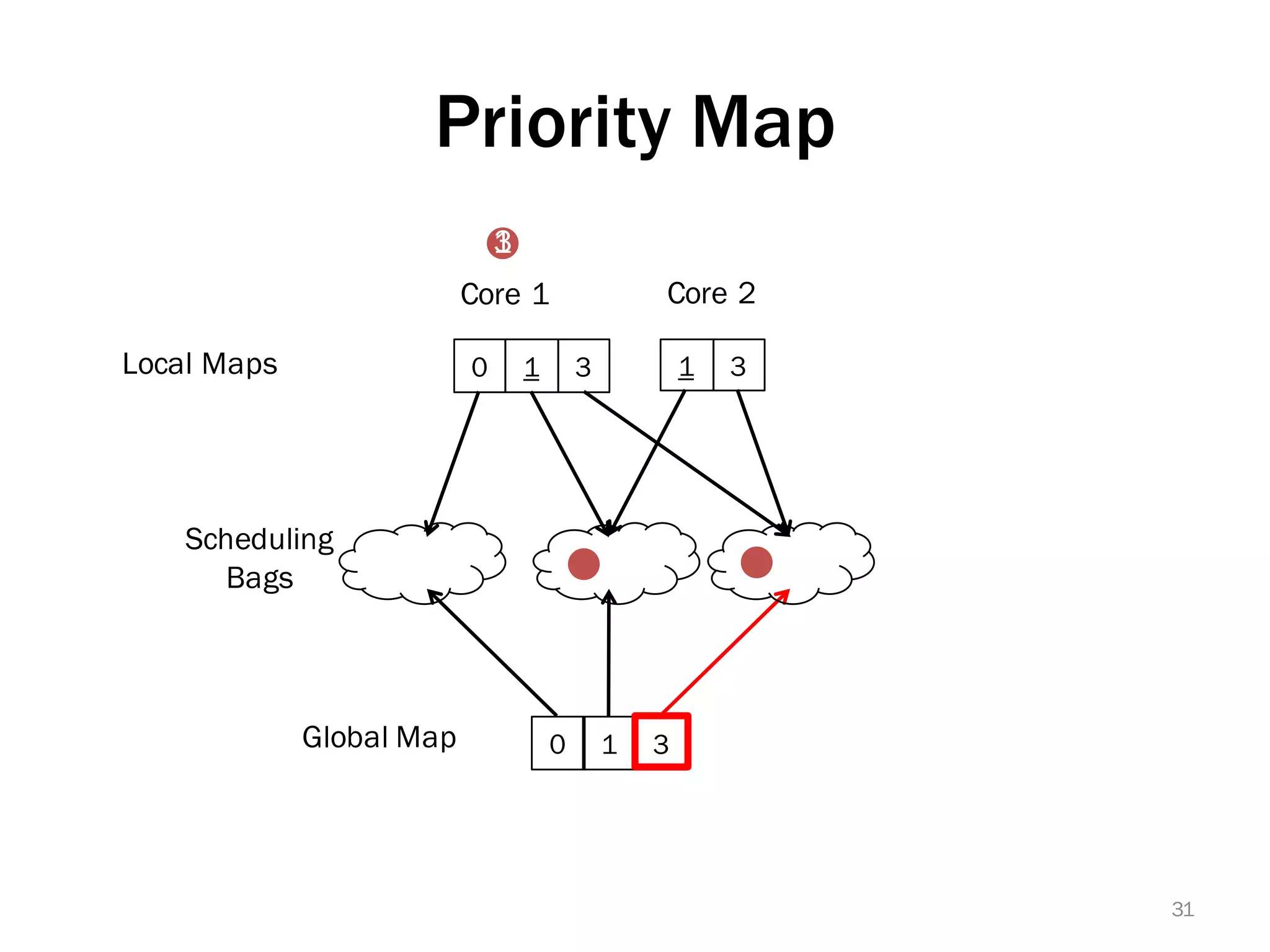
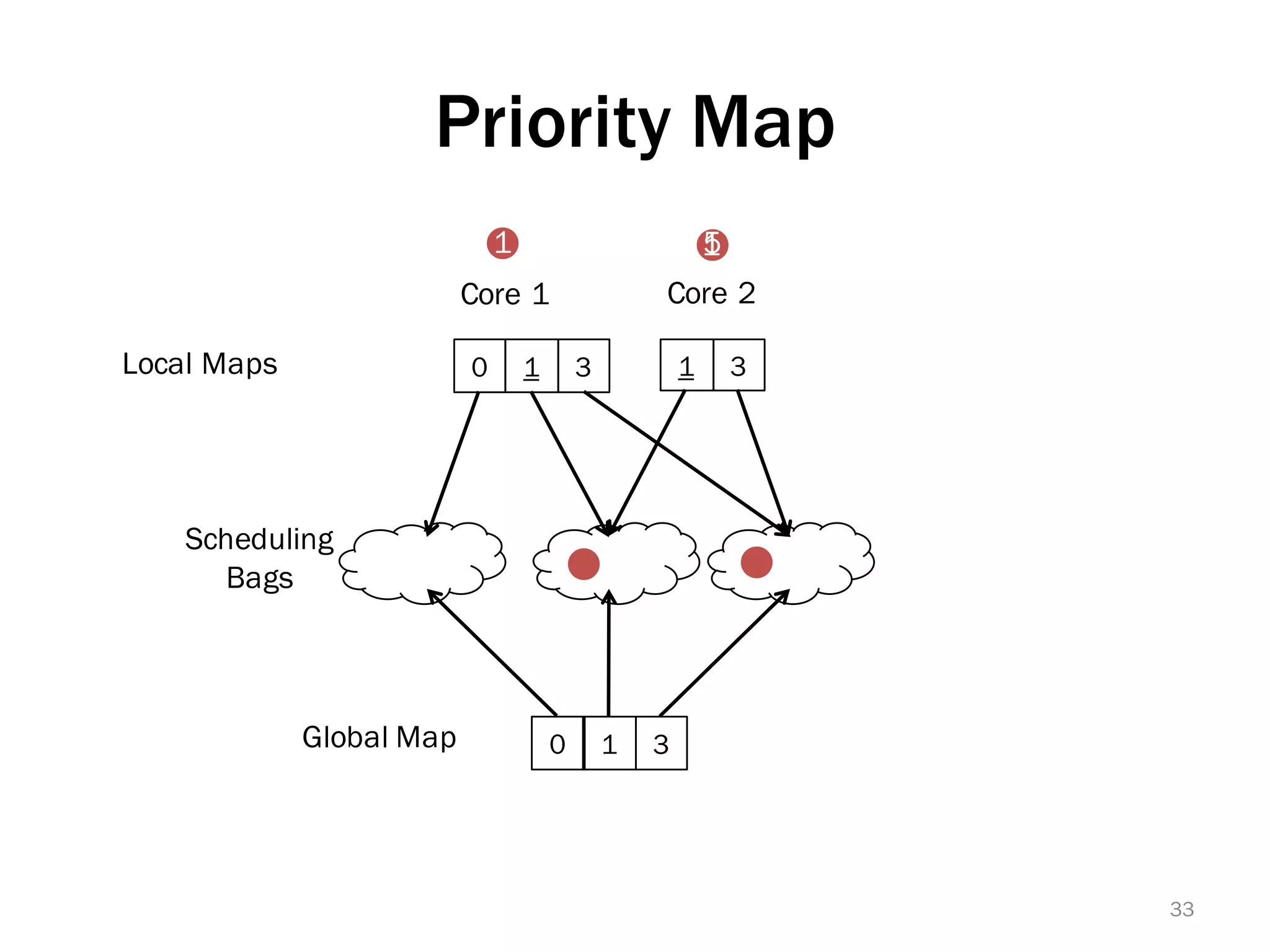
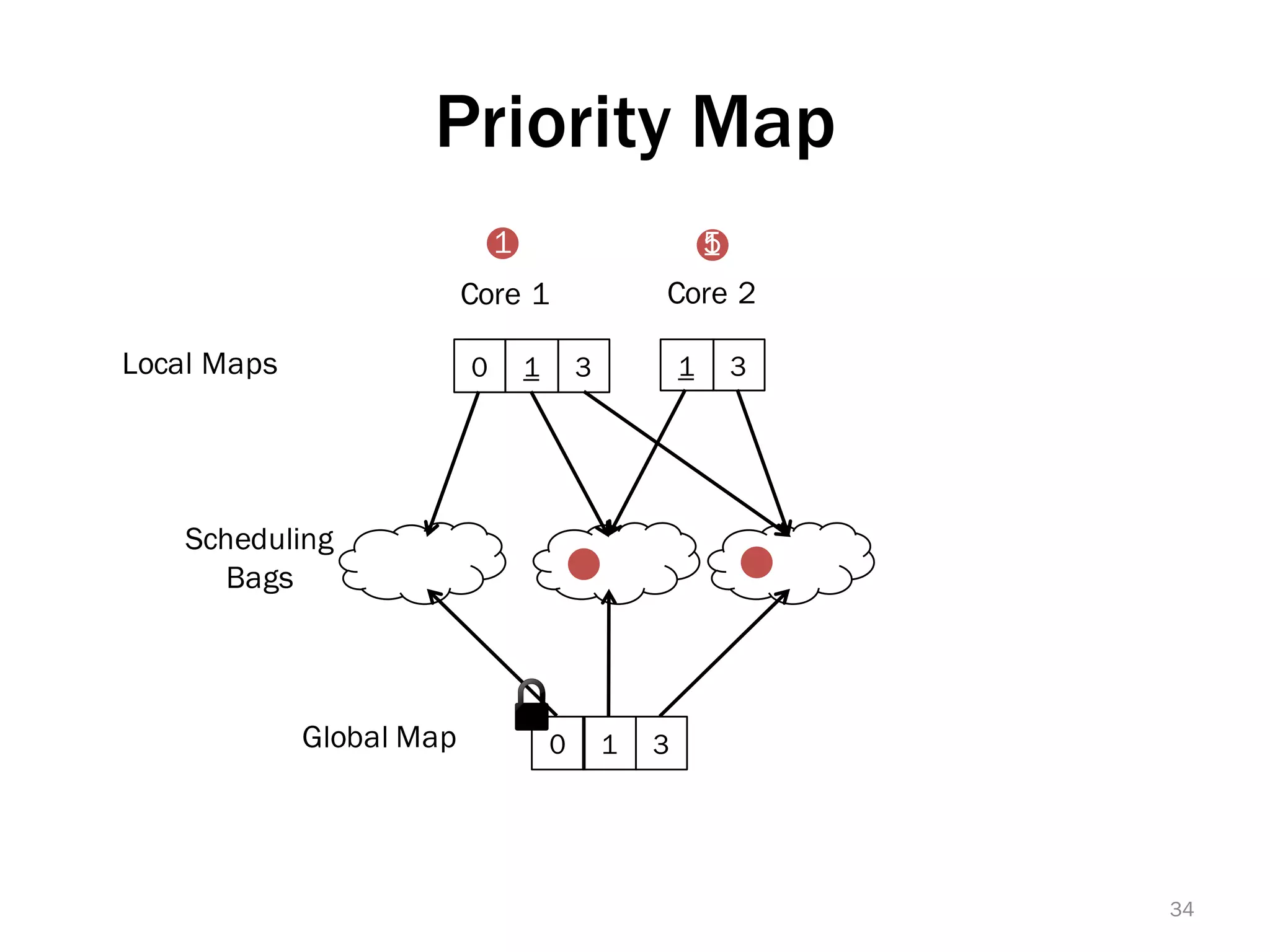
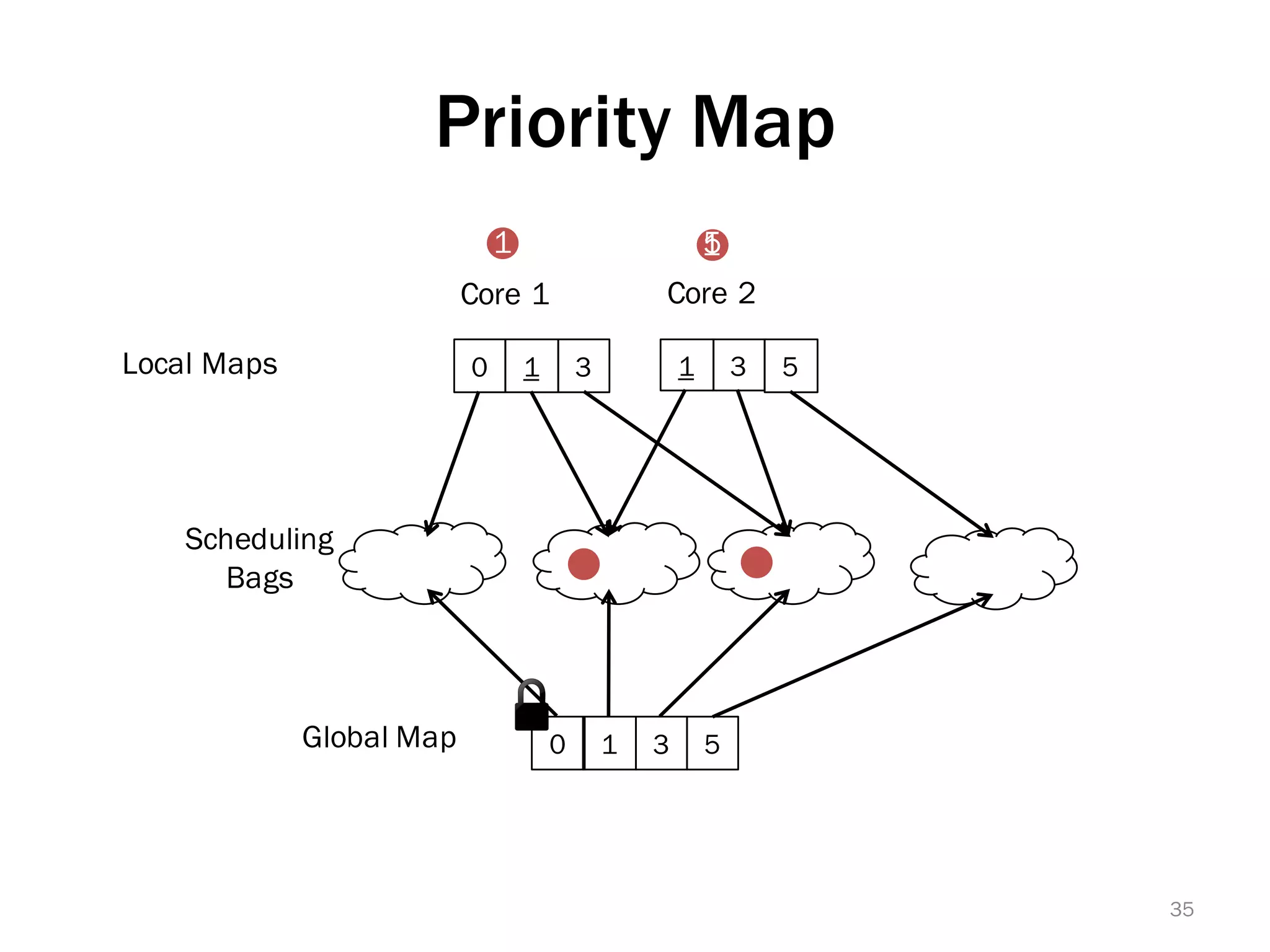
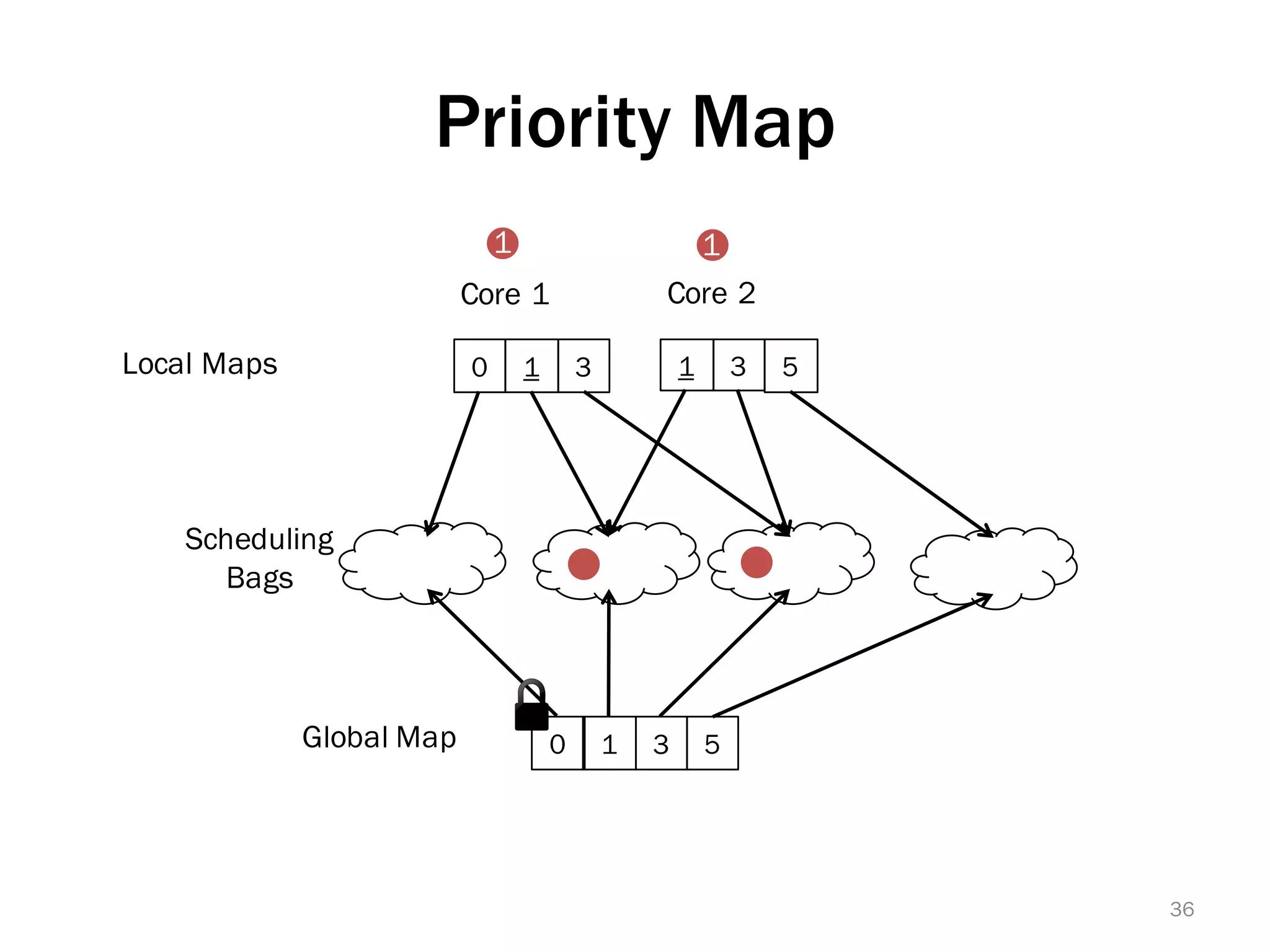
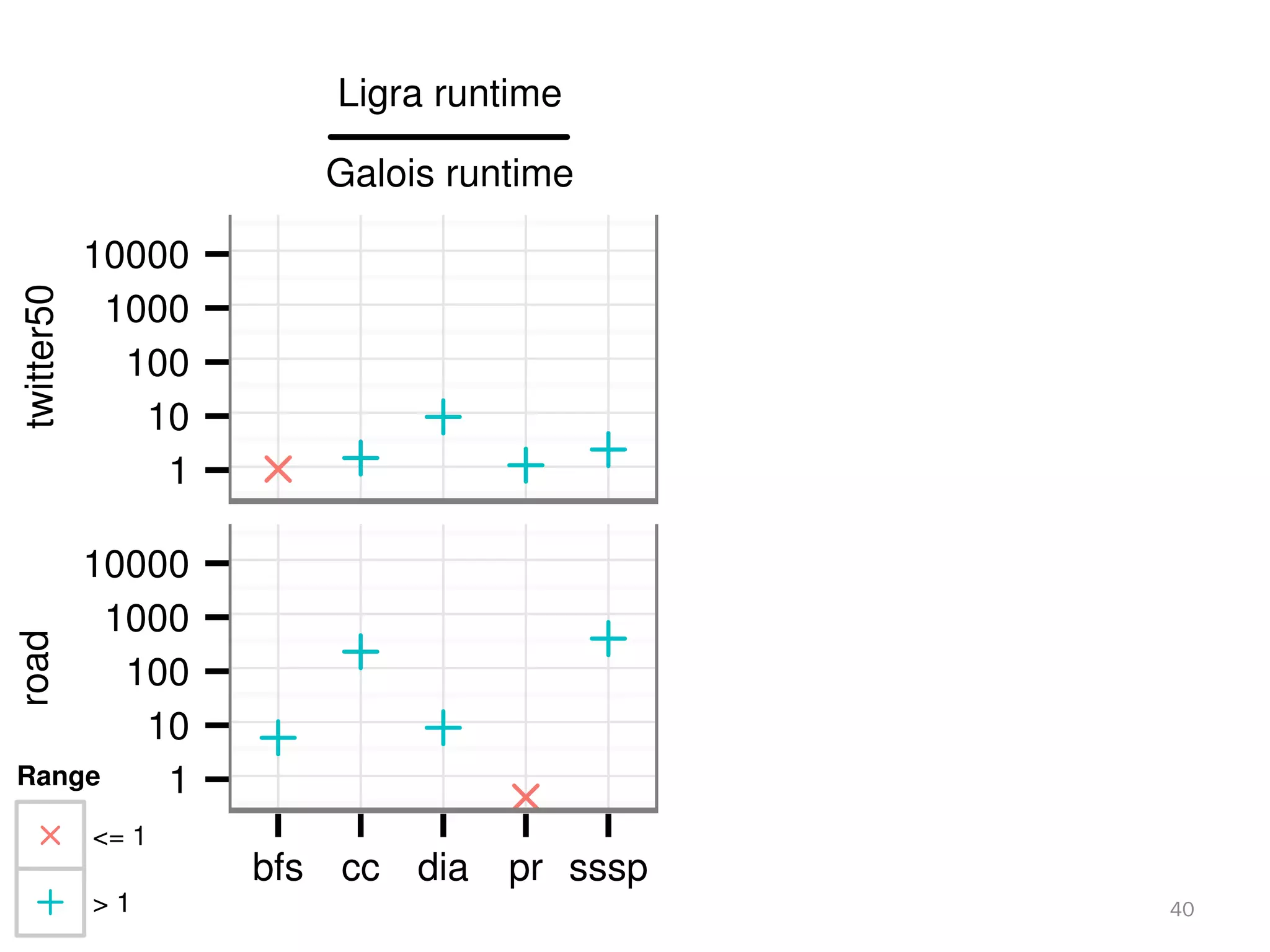
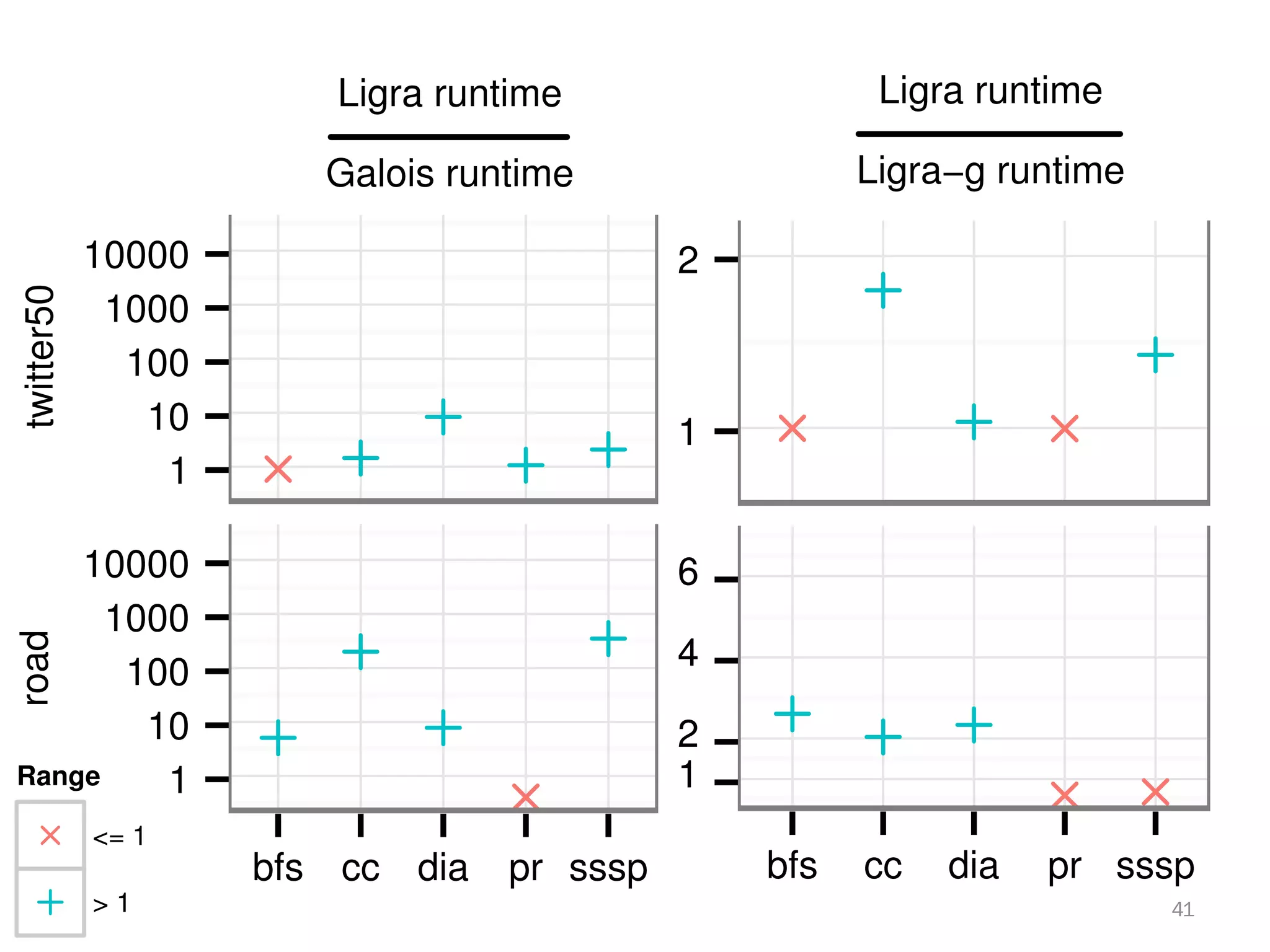
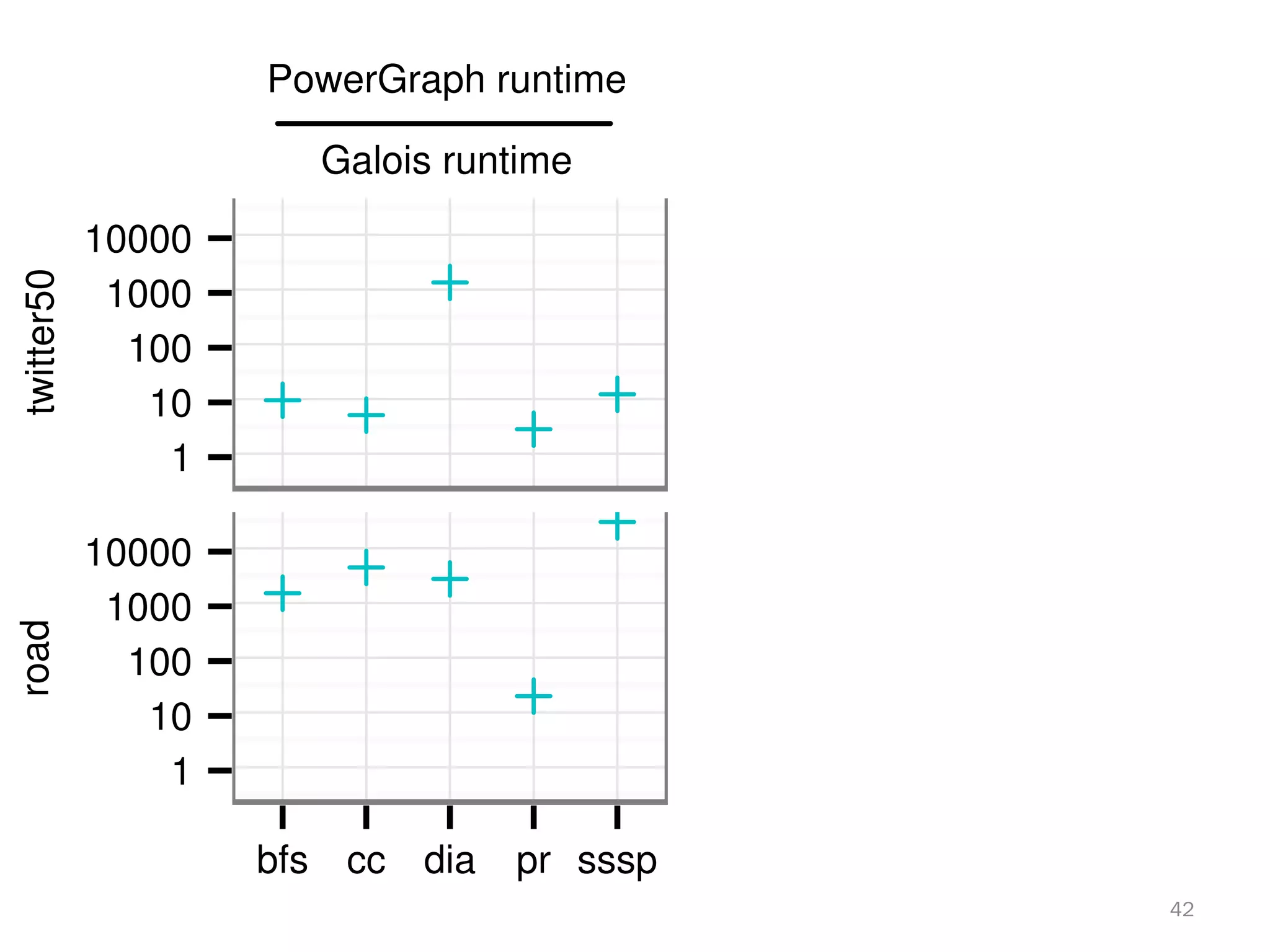
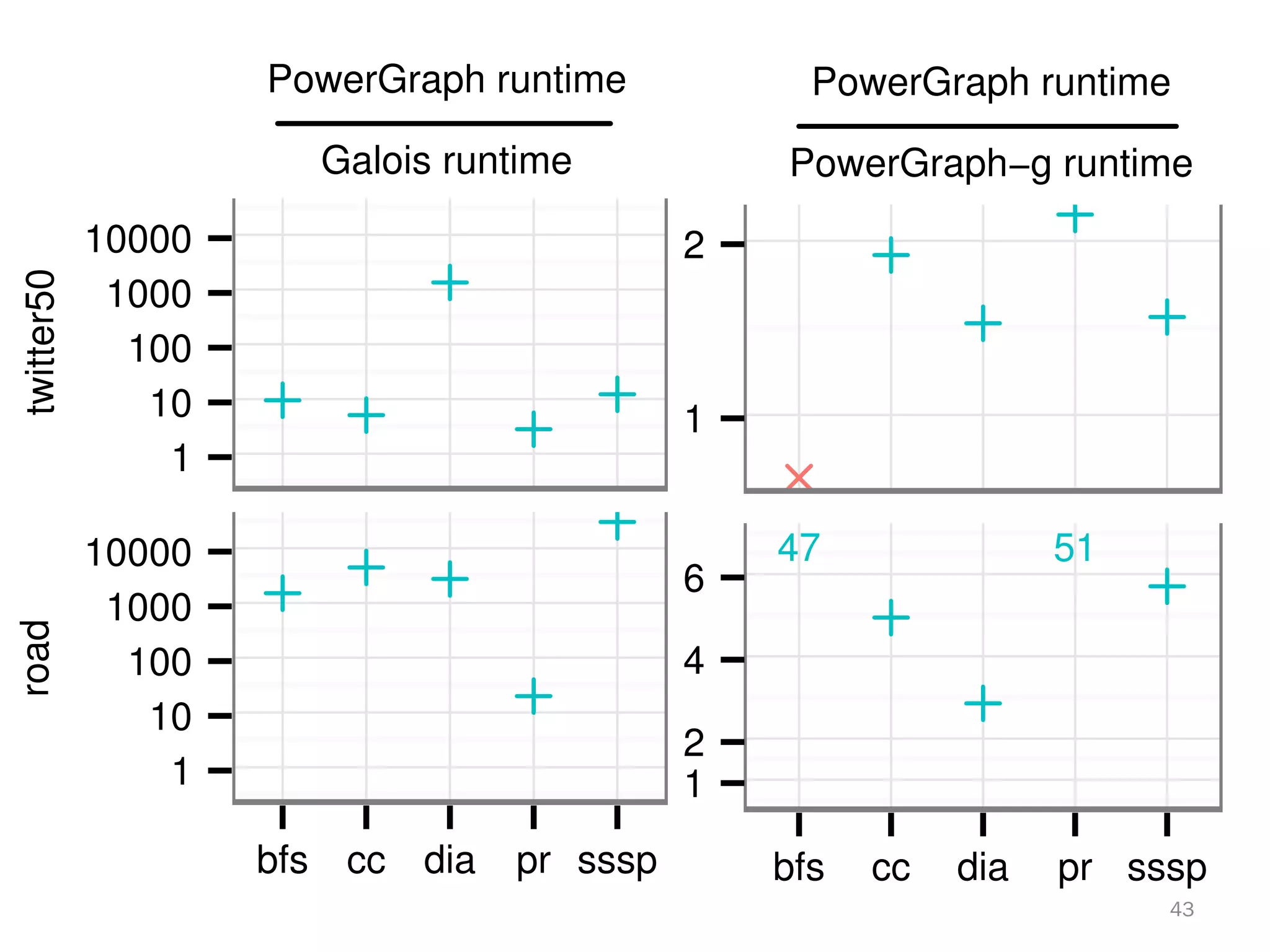
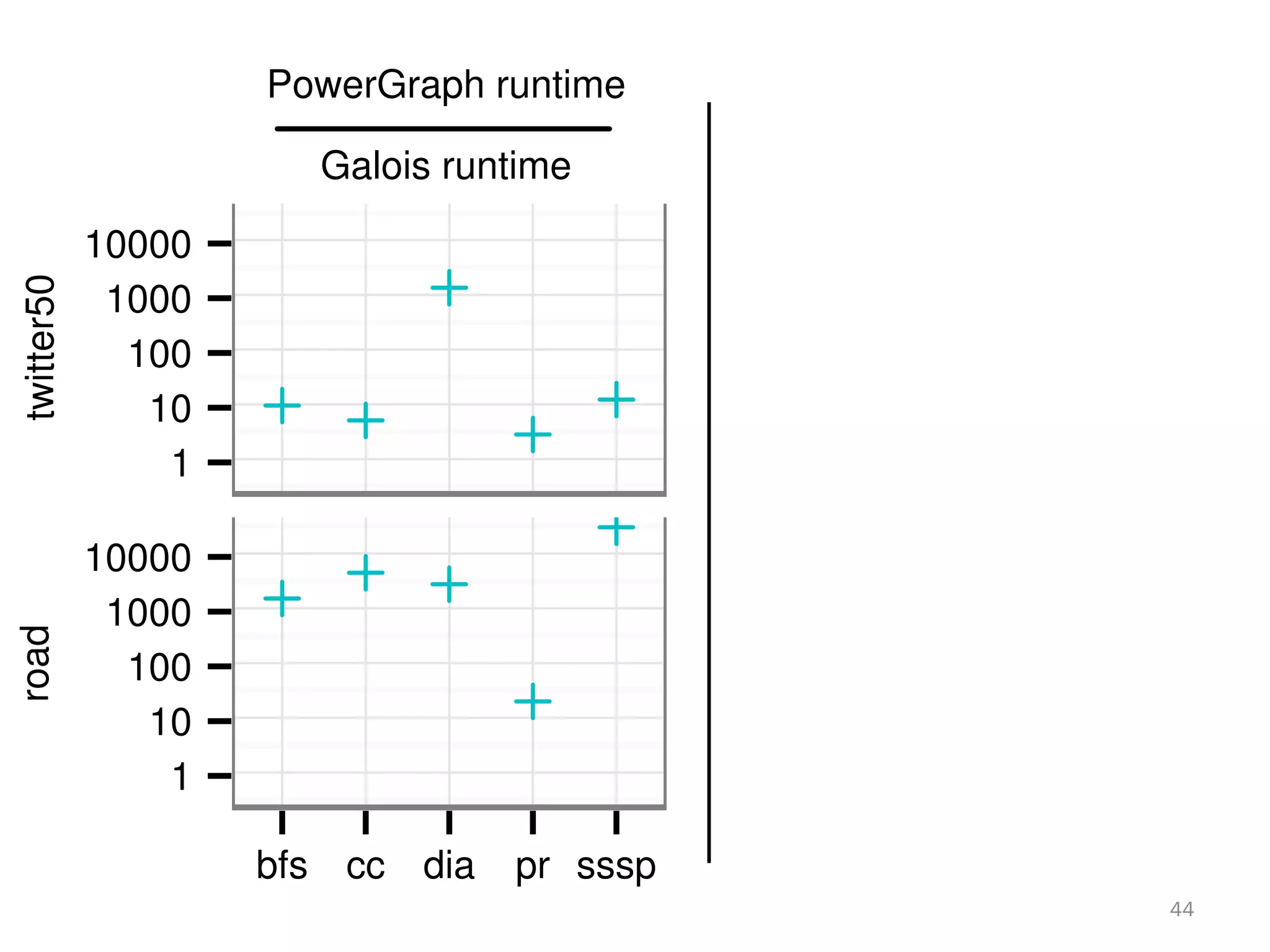
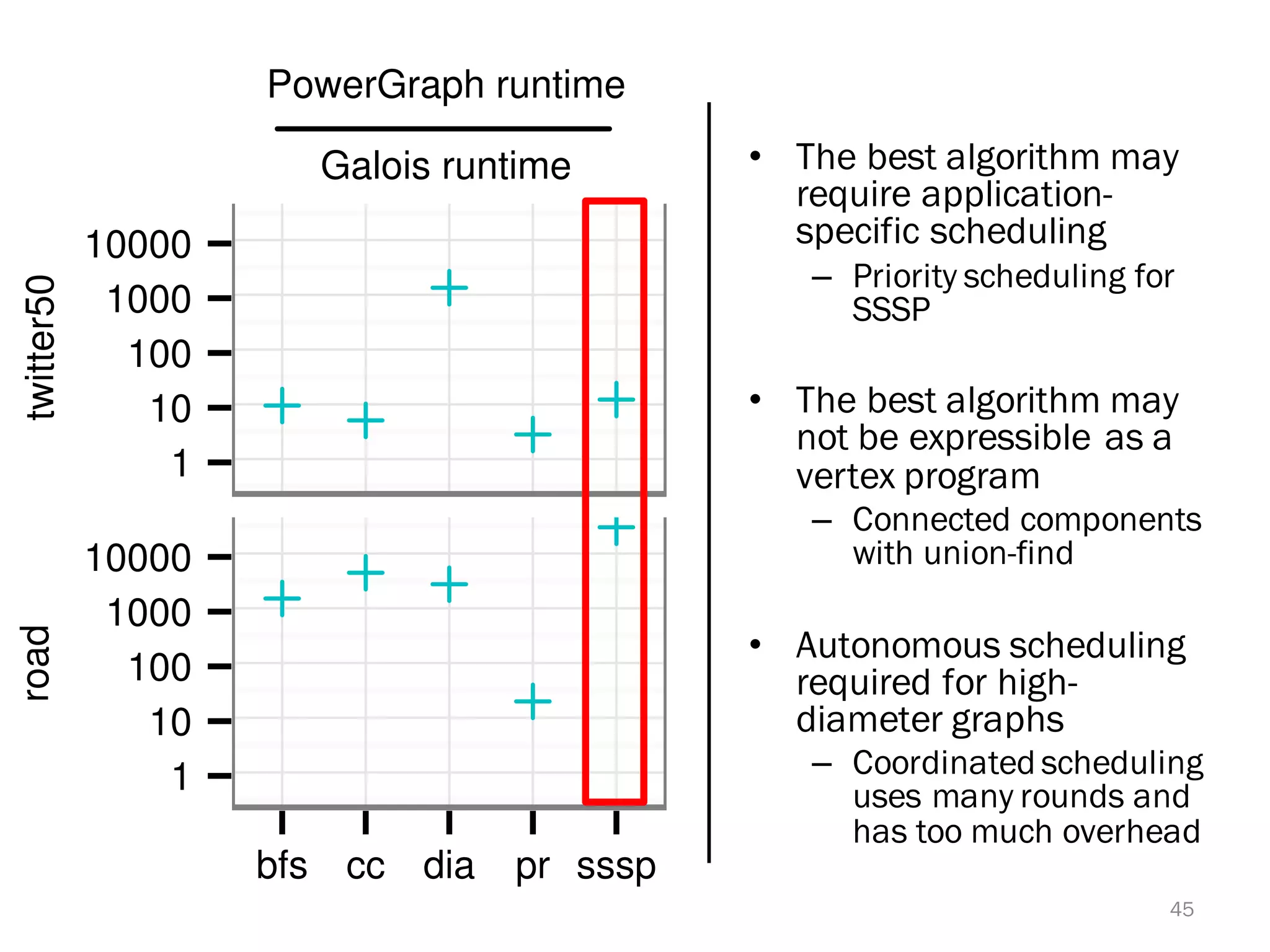
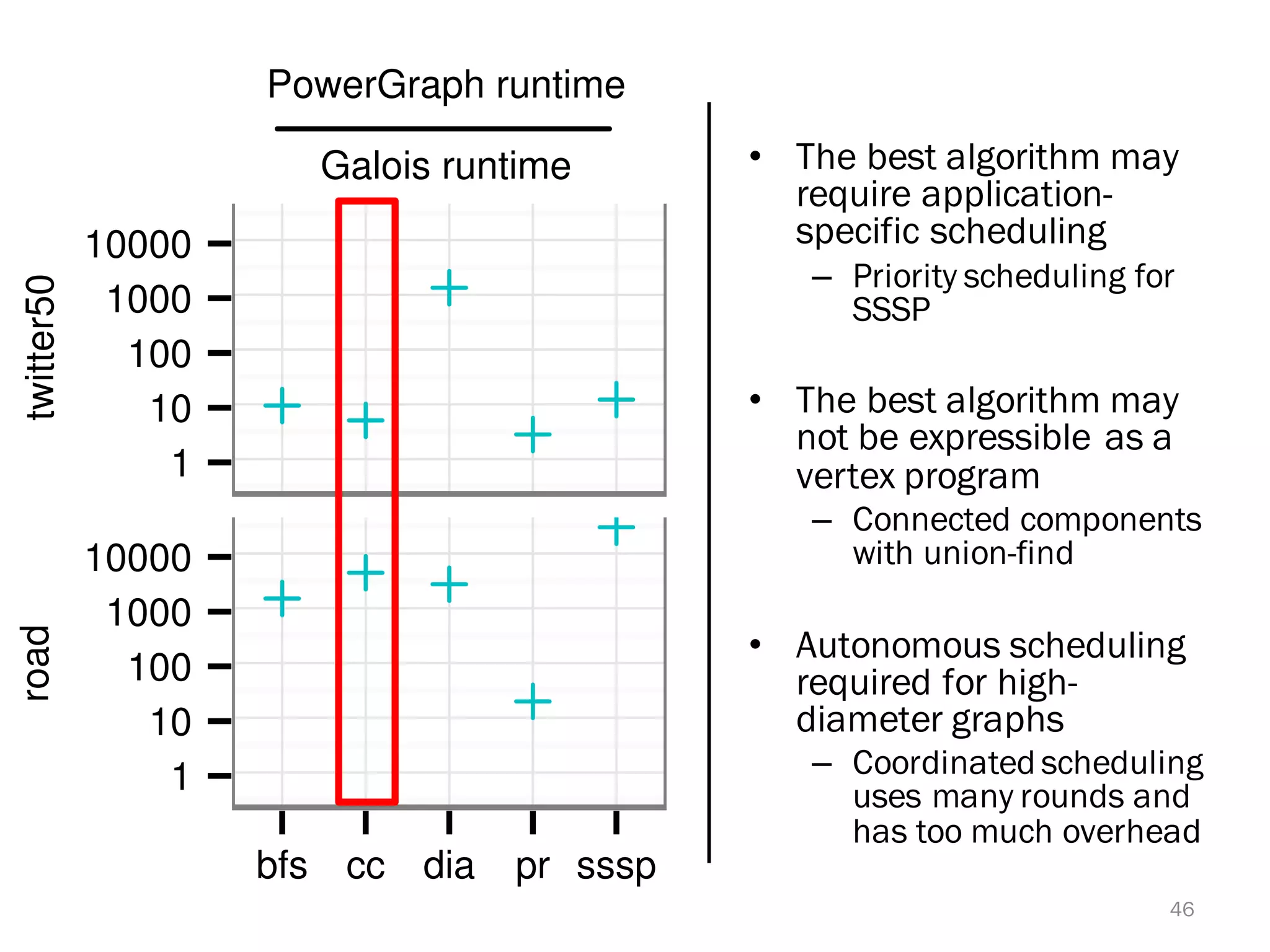
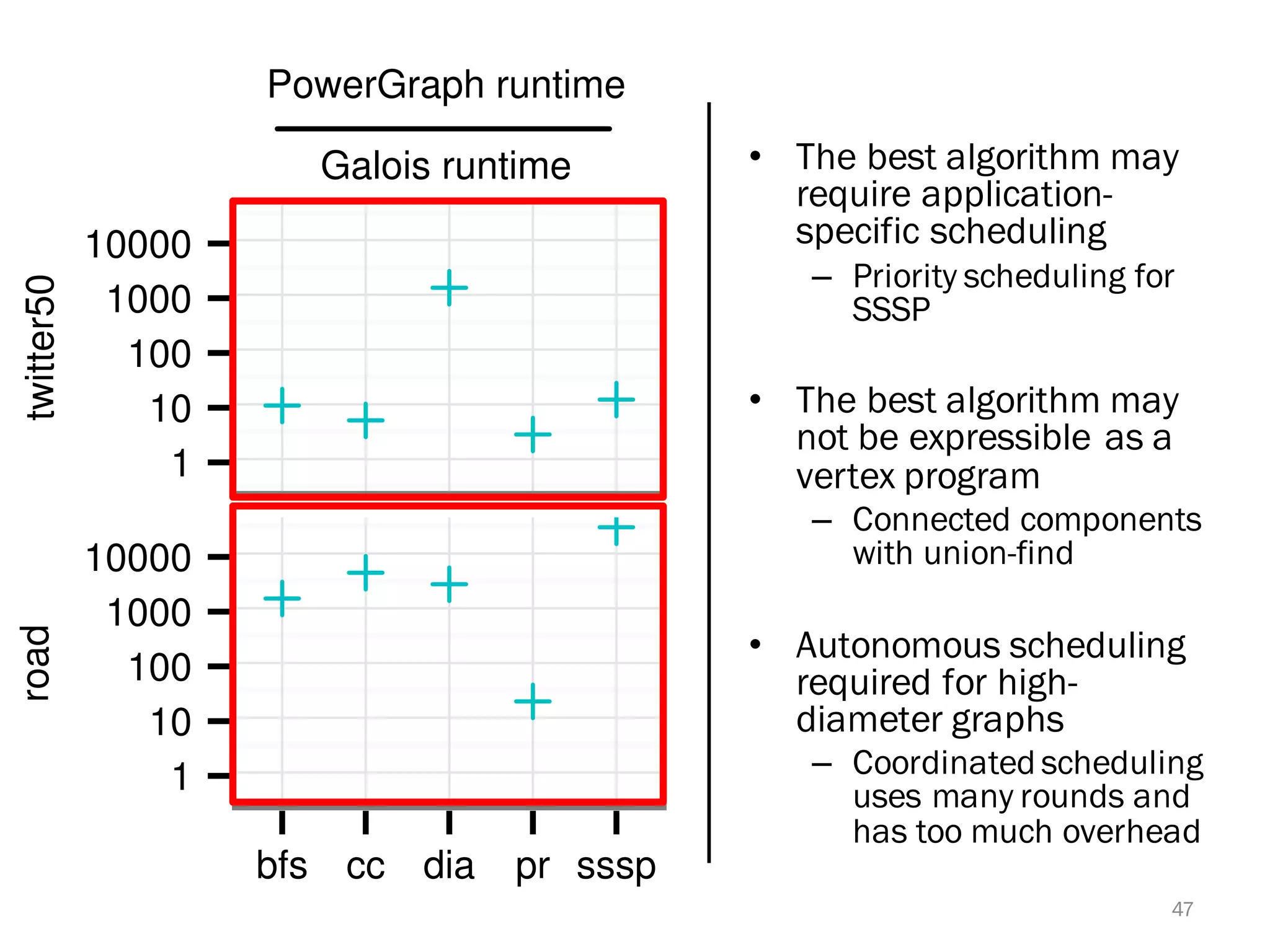
The document discusses a lightweight infrastructure for graph analytics based on the Galois system, which improves efficiency in computing properties of graphs. It highlights scalable priority scheduling that enables faster execution compared to existing graph DSLs, demonstrating significant performance gains across various algorithms, especially for applications like single-source shortest paths. The Galois programming model is noted for its generality and scalability, making it suitable for high-performance graph processing.