This document discusses binary arithmetic and how it works using boolean logic. It provides examples of adding binary numbers and what happens in overflow conditions when the results exceed the bit limit. The key concepts covered are: 1) Binary addition employs the same process as decimal addition, carrying values to the next column when the sum exceeds the base. 2) Overflow occurs when the result of an addition does not fit in the allocated bit space, with part of the value lost. Programs can detect overflow as an error. 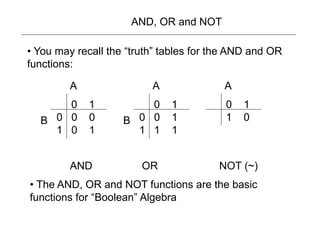3) Binary operations can be represented using boolean logic functions like AND, OR and NOT. Single bit adders use these functions with inputs A, B, and a carry in to calculate outputs for the

1. Binary Arithmetic
• Adding Binary numbers
• Overflow conditions
• How does it all work?
• AND, OR and NOT

2. Decimal Addition
• You are probably already familiar with adding
decimal numbers
7
+2
9
5
+1
6
2
+3
5
• You also know that when the addition of two
numbers exceeds the base, a value is “carried” over
to the next column
7
+ 5
1 2
1 Carry the “1”

3. Binary Addition
• Adding binary numbers employs the same
procedures as adding decimal numbers:
00
+00
00
01
+00
01
00
+01
01
• As with decimal addition, when the addition of two
numbers exceeds the base value, the value is
“carried” over to the next column
01
+01
10
1 Carry the “1”

4. Binary Addition Examples
01001100
01101010
10110110
11001100
00110011
11111111
01111111
00000001
10000000
• What happens when we have the following case?
11
+11
???
1 Carry the “1”

5. More Binary Addition Examples
01111111
01000001
11000000
10001100
00111011
11000111
01111111
01001001
11001000
11111111
00000001
????????
• What happens when we get the following case?
(note: assume that we are limited to 8 bits)

6. Overflow
11111111
00000001
00000000
• In the following case, we have a condition called
“overflow”. The result may be somewhat unexpected
1 Carry the “1”
• When adding two numbers, it is possible that the
result will not fit within the space we have provided.
The addition completes, but part of the value is lost.
• Luckily, overflow is often considered to be an error
condition, so the program “knows” that this has
happened and can take appropriate action.

7. How does it all work?
• In the first week of lectures, we discussed vacuum
tubes, relays, and transistors
• As we went through the discussion, I asked, “How
could you add two numbers using switches?”
• I didn’t expect an answer, but I did show how switches
could be set up to implement the AND function and the
OR function.

8. AND, OR and NOT
• You may recall the “truth” tables for the AND and OR
functions:
0 1
0 0 0
1 0 1
0 1
0 0 1
1 1 1
A
B
A
B
AND OR
• The AND, OR and NOT functions are the basic
functions for “Boolean” Algebra
0 1
1 0
A
NOT (~)

9. Binary Arithmetic/AND and OR
• All binary arithmetic can be represented using
boolean algebra
• Each 1-bit adder has 3 inputs: A, B and CarryIn
• Each 1-bit adder has 2 output: C and CarryOut
CIN 0 0 0 0 1 1 1 1
A 0 0 1 1 0 0 1 1
B 0 1 0 1 0 1 0 1
C 0 1 1 0 1 0 0 1
COUT 0 0 0 1 0 1 1 1

10. Boolean Equations for Addition
CIN 0 0 0 0 1 1 1 1
A 0 0 1 1 0 0 1 1
B 0 1 0 1 0 1 0 1
C 0 1 1 0 1 0 0 1
COUT 0 0 0 1 0 1 1 1
C = (~A and B and ~CIN) or (A and ~B and ~CIN) or
(~A and ~B and CIN) or (A and B and CIN)
COUT= (A and B) or (A and CIN) or (B and CIN)