This document describes a coding challenge problem involving seating arrangements in a library reading room while maintaining social distancing.
The key details are:
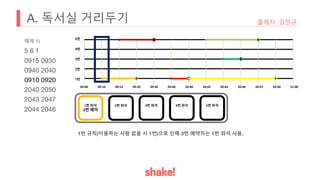
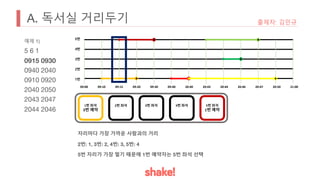
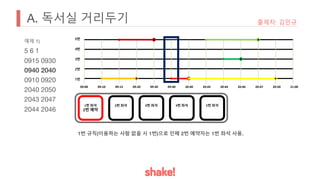
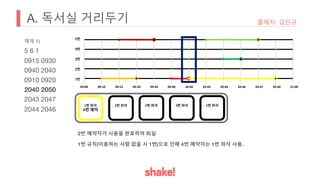
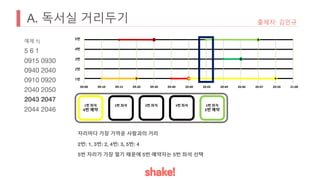
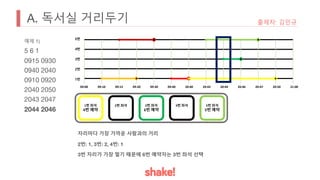
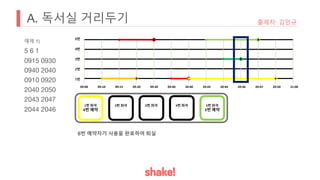
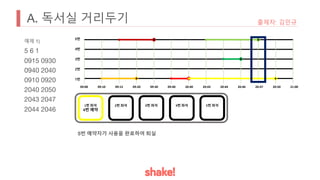
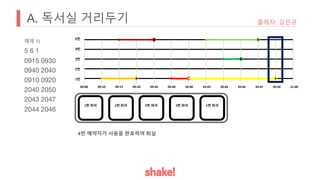
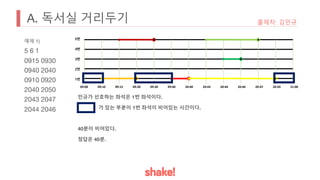
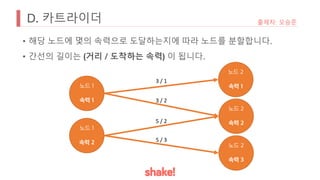
- Seating is assigned based on keeping the greatest distance from the nearest occupied seat. Empty seats are prioritized over more distant occupied seats.
- An example seating arrangement is provided over time as people arrive and leave.
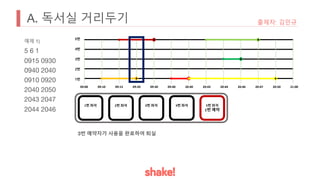
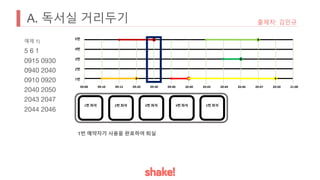
- The task is to calculate how long the preferred seat of the problem author is available.
The problem is modeled as a simulation over discrete time steps to track the seating status and calculate the desired result. The time complexity is analyzed as O(T*N) where T is the number of time steps and N is the number of reservations.










![B. 인물이와 정수
• Solution
• Parametric Search
최적화 문제를 결정 문제로 바꾸어 푸는 방법
탐색하려는 범위 [s, e]가 있으면 중간 값 mid = (s+e) / 2를 잡아 문제의
조건을 만족하는지 확인
이후 탐색할 범위를 절반으로 줄여가는 방식이다.
출제자: 손병호](https://image.slidesharecdn.com/2020shakesolution-210315074639/85/2020-shake-solution-23-320.jpg)




![C. 크롬
• DP table을 적절하게 구성하여 해결하는 배낭 문제입니다.
• 만약 dp[i][j][k] 를
• i 번째 탭까지 사용할 때
• cpu j, memory k 를 만들 수 있는
• 중요도 합의 최솟값
• 로 정의한다면
• 시간 복잡도는 100 * 1000 * 100000
= Time Limit 이 발생합니다.
출제자: 오승준](https://image.slidesharecdn.com/2020shakesolution-210315074639/85/2020-shake-solution-28-320.jpg)
![C. 크롬
• 이때 중요도의 합은 최대 500이고, 메모리만 최대값이 큰 것을
활용해서 새롭게 dp table을 정의해봅시다.
• dp[i][j][k] =
• i 번째 탭까지 사용할 때
• cpu j, priority k 를 만들 수 있는
• 메모리의 최댓값
• 시간 복잡도는 100 * 1000 * 500 으로 줄어들게 됩니다.
출제자: 오승준](https://image.slidesharecdn.com/2020shakesolution-210315074639/85/2020-shake-solution-29-320.jpg)
![C. 크롬
• 관계식은 배낭 문제와 비슷하게 구할 수 있습니다.
• dp[i][j][k] =
max(dp[i][j][k], dp[i - 1][j - tab.cpu][k - tab.priority] + tab.memory)
• dp[i][j][k] ≤ Memory을 만족하는 가장 작은 k 값이 정답입니다.
출제자: 오승준](https://image.slidesharecdn.com/2020shakesolution-210315074639/85/2020-shake-solution-30-320.jpg)







![E. Close to You 출제자: 김동이
인접 행렬의 거듭제곱
정사각 행렬인 인접 행렬 E에 대해 다음이 성립한다.
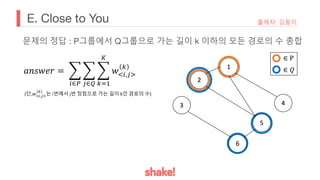
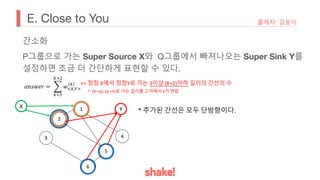
• 𝐸&의 원소 𝐸& 𝑖 [𝑗]는 정점 i 에서 정점 j 로 가는 경로의 경우의 수를 나타낸다.
즉, 변형한 그래프의 인접 행렬을 E 라고 할 때 문제의 정답은 다음과 같다.
X Y
• N은 100 이하이므로 (N+2)^2 행렬의 제곱은 쉽다.
• K가 크므로 행렬의 빠른 제곱을 구현하면 된다.
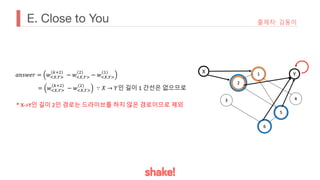
𝑎𝑛𝑠𝑤𝑒𝑟 = 𝐸!%&
𝑋 𝑌 − 𝐸&
[𝑋][𝑌]
시간 복잡도는 𝑂(log& 𝐾 7 𝑁&
)](https://image.slidesharecdn.com/2020shakesolution-210315074639/85/2020-shake-solution-42-320.jpg)


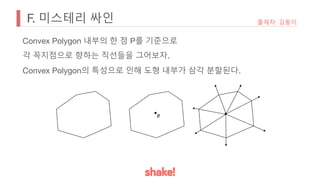





![H. 대세는 바이러스야
• 하나의 입구를 먼저 관찰해보자.
• 문제를 단순화해 선형으로 관찰해보자.
• 보스는 언제나 죽어야 하므로, 노드의 모든 수 g[i] = gcd(g[1], g[i])
• 오른쪽을 고정했을 때 가능한 연속 구간 gcd의 종류는?
출제자: 홍준표
1 2 3 4 5 6 7](https://image.slidesharecdn.com/2020shakesolution-210315074639/85/2020-shake-solution-54-320.jpg)
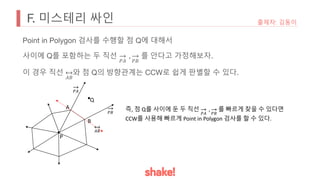
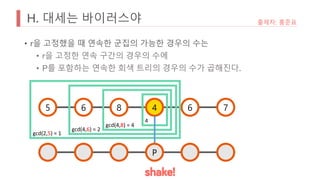
![H. 대세는 바이러스야
• 고려하는 수가 많아질수록, gcd 값은 작아진다.
• 고정된 g[r]의 소인수 단위로 감소
• r이 고정된 모든 연속 구간에서 가능한 gcd 수의 종류는 최대 log(g[r]) 개
임이 보장된다.
출제자: 홍준표
5 6 8 4 6 7
4
gcd(4,8) = 4
gcd(4,6) = 2
gcd(2,5) = 1](https://image.slidesharecdn.com/2020shakesolution-210315074639/85/2020-shake-solution-55-320.jpg)
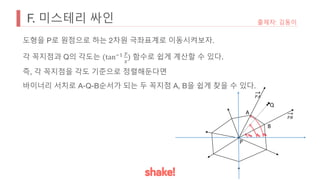
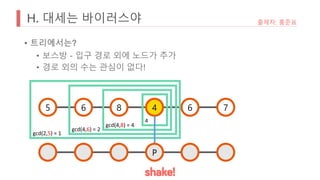
![H. 대세는 바이러스야
• 고정된 r이 한 칸 이동하면 어떻게 변할까?
• 전에 고려된 모든 수 X가 gcd(X, g[r + 1]) 된다.
• 길이 1인 g[r + 1] 이 목록에 추가
• 이런 식으로 점차 확장하면 모든 연속 구간의 gcd 합을 구할 수 있다.
출제자: 홍준표
5 6 8 4 6 7
4
gcd(4,6)=2
gcd(4,8) = 4
gcd(4,6)=4
gcd(4,6) = 2
gcd(2, 6)=2
gcd(2,5) = 1
gcd(1, 6) = 1](https://image.slidesharecdn.com/2020shakesolution-210315074639/85/2020-shake-solution-56-320.jpg)
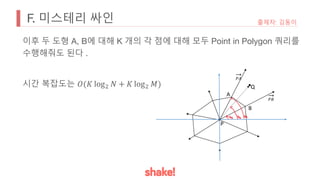
![H. 대세는 바이러스야
• cnt[x] : x의 부모와 연결했을 때 x의 부모와 연속할 수 있는 구간
의 개수
• path 위에 구간을 선택하지 않았을 때 또한 cnt를 활용해 고려한
다. 이때는 보스만을 죽이므로 g[1]
• cnt를 활용해 다이나믹 프로그래밍을 하면 각 입구에서의 치트키
합을 구할 수 있다.
• 주의! cnt는 1e9+7의 배수일 수 있기 때문에 modular inverse를
활용하면 오답을 받을 수 있다.
• 시간 복잡도 :
출제자: 홍준표
x
𝑐𝑛𝑡[𝑥] = 1 + *
< ∈ >?@ ABCDE
𝑐𝑛𝑡[𝑦]
𝑂(𝑁𝑙𝑜𝑔:𝑋)](https://image.slidesharecdn.com/2020shakesolution-210315074639/85/2020-shake-solution-59-320.jpg)