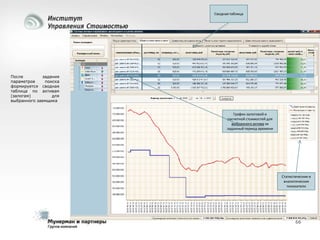
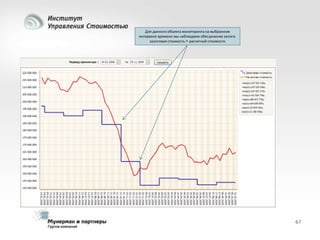
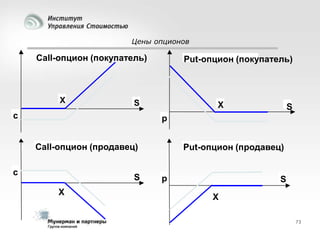
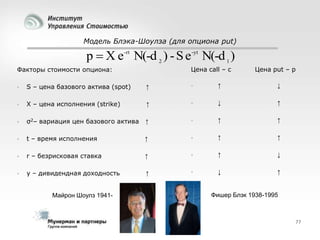
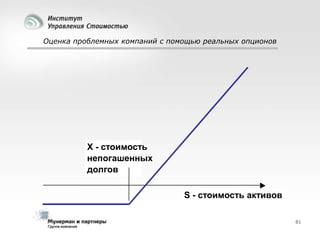
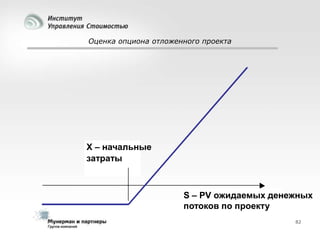
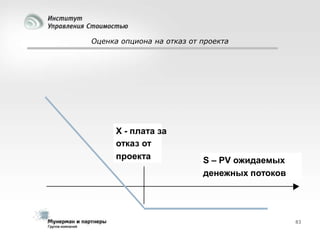
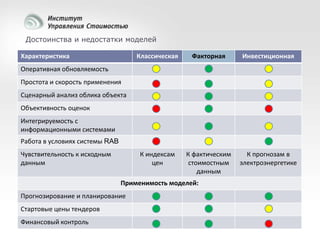
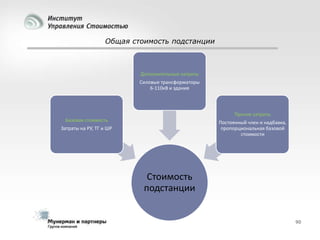
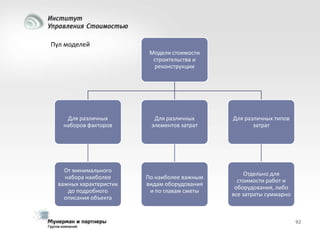
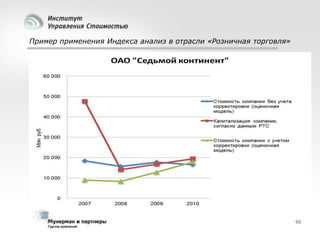
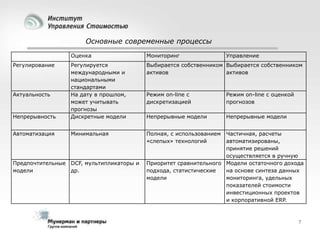
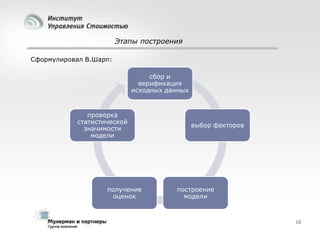
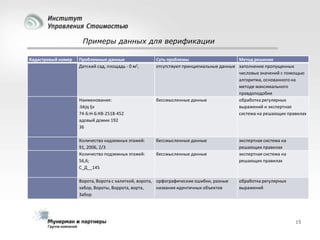
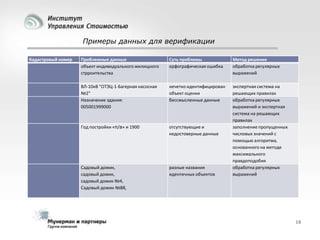
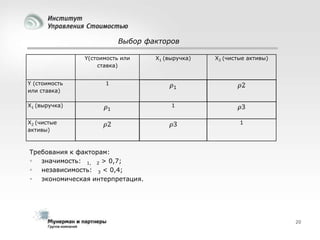
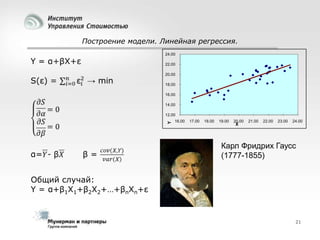
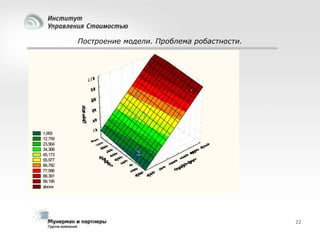
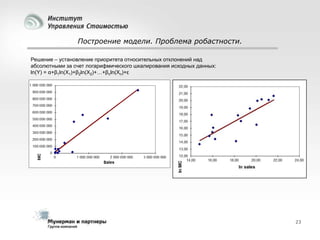
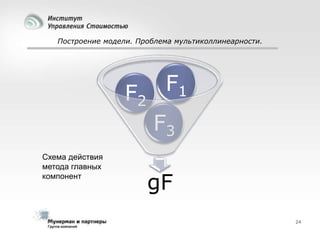
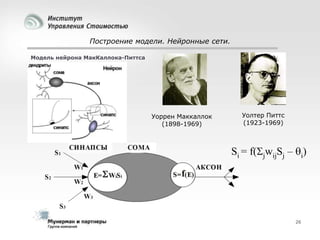
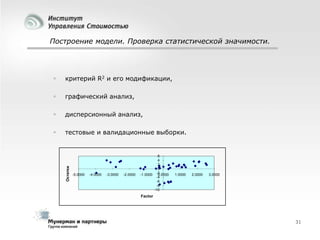
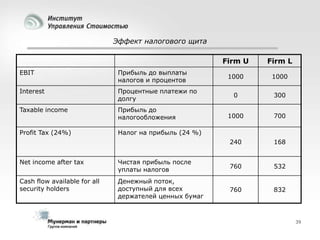
Документ рассматривает современные модели и методы стоимостной оценки, управления стоимостью и мониторинга экономических показателей, акцентируя внимание на макроэкономических предпосылках и различных экономических парадигмах, таких как классическая, кейнсианская и монетаристская. Он также анализирует историческое развитие оценочных моделей, включая дисконтированные денежные потоки и современные статистические подходы, а также механизмы верификации данных и методы анализа. В заключение, подчеркнута важность использования моделей и методов для повышения эффективности оценки и минимизации транзакционных издержек.

1. Современные модели, методы и информационное
обеспечение стоимостной оценки, управления
стоимостью и мониторинга экономических
показателей
1

2. Введение
2

3. Макроэкономические предпосылки
Экономическая
парадигма
Классическая
Суть парадигмы
Подход к стоимости
Недостатки парадигмы
Роль управления стоимостью
Невмешательство государства в
экономические процессы.
Конкурентные рынки сами
формируют успешное
экономическое развитие.
Классическое определение –
стоимость формируется абсолютно
свободными и информированными
покупателями и продавцами
Учитываются в первую очередь
рыночные стоимости активов, как
наиболее достоверные
посредством постоянного
мониторинга.
Кейнсианская
Государство должно управлять
экономическими процессами,
преследуя обеспечение всеобщей
занятости.
Игнорирование стоимостного
анализа. Убежденность в
случайном формировании цен на
рынках.
Свободные рынки не формируются,
образуются провалы (gap).
Требуются вмешательство
государства для устранения
вызванных этими провалами
кризисов.
В результате игнорирования
стоимостной проблематики
складывается ситуация, в которой
организация всеобщей занятости
приводит к неконтролируемому
росту бюджетных расходов, без
достижения значимых результатов.
Монетаристская
Государство должно управлять
экономическими процессами, но не
через хозяйственную активность, а
через подбор оптимальных
параметров денежно-кредитной
политики.
Государство и общество, через
экономические институты должно
добиваться снижения
транзакционных издержек, как в
макроэкономическом аспекте
(общественный договор), так и в
микроэкономическом.
Из всех подходов к стоимости
наиболее приоритетным
полагается анализ
дисконтированных денежных
потоков.
Отрыв стоимости финансовых
активов от реального сектора
экономики.
Учитываются денежные потоки в
неразрывной связи со стоимостным
ядром (RIM).
Не выявлен
Не выявлены
Объединяя все лучшее от
различных подходов, создает
эффективный инструмент для
снижения транзакционных
издержек.
Институциональная
Учитываются рыночные стоимости
осуществления инвестиционных
проектов и производится оценка
полезности их реализации (УПС).
3

4. Макроэкономические предпосылки
Современные исследования:

Закон Гудхарта – отказ от всеобъемлющих решений;

Поведенческая экономика;

Отличия реального человека от рационального экономического агента;

Современные рейтинговые и скоринговые модели;

Конвергенция с другими науками;

Использование больших данных, data mining, открытых данных;

Использование сложных моделей обработки данных;

Постановка экономических экспериментов.
4

5. Историческое введение – стоимость бизнеса











20-е годы – первые модели стоимостного анализа от Грэхема-Ри
к Эдвардсу-Бэллу;
с 1948 по 1959 – DDM, модель Гордона-Шапиро, WACC в качестве
ставки;
1959 – теорема Миллера-Модильяни, дискуссия 59;
70-е годы – работы Марковица и CAPM Шарпа;
80-е годы концепция VBM Коупленда;
90-е – модели реальных опционов, остаточного дохода, EVA
Стерна, Дамодаран и др;
1999 – модель Бакши-Ченга;
2002 – агрегационная теорема Типпета-Кука-Эштона;
2006 – dirty surplus, непрерывная стоимость;
2008 – модель Адама;
2005 – EBM.
5

6. Историческое введение – стоимость для акционеров





с 1948 – формирование корпораций и конфликта
менеджмента и акционеров;
50-е годы – американская (прибыль) и европейская (рынки
сбыта) школа;
70-е годы – концепция оплаты труда менеджеров опционами;
80-е годы BSC-KPI и концепция VBM Коупленда;
2005 – EBM.
Том Коупленд
6

7. Основные современные процессы
Оценка
Мониторинг
Выбирается собственником Выбирается собственником
активов
активов
Непрерывность
Регулируется
международными и
национальными
стандартами
На дату в прошлом,
может учитывать
прогнозы
Дискретные модели
Автоматизация
Минимальная
Полная, с использованием
«слепых» технологий
Регулирование
Актуальность
Предпочтительные DCF, мультипликаторы и
модели
др.
Управление
Режим on-line с
дискретизацией
Режим on-line с оценкой
прогнозов
Непрерывные модели
Непрерывные модели
Частичная, расчеты
автоматизированы,
принятие решений
осуществляется в ручную
Приоритет сравнительного Модели остаточного дохода
подхода, статистические
на основе синтеза данных
модели
мониторинга, удельных
показателей стоимости
инвестиционных проектов
и корпоративной ERP.
7

8. Принципиальная схема системы мониторинга и управления стоимостью
8

9. Статистические модели
9

10. Этапы построения
Сформулировал В.Шарп:
сбор и
верификация
исходных данных
проверка
статистической
значимости
модели
получение
оценок
выбор факторов
построение
модели
10

11. Сбор и верификация исходных данных для оценки бизнеса

источники информации в РФ:
,Бюллетень
«Государственное имущество», Бюллетень «Рынок слияний и поглощений»

источники информации в мире:

отраслевые классификаторы ОКВЭД, Fama/French industry classification;

коды SIC (Standard Industrial Classification) и NAICS (North American Industry Classification
System);

проблема различий в финансовой отчетности;

проблема даты окончания финансового года;

проблемы пересчета per share data;

проблемы величины продаваемых пакетов;

проблемы сбора производственных данных.
11

12. Сбор и верификация исходных данных для оценки активов
Оценка активов – методы верификации:

семантические анализаторы,

матрицы граничных значений,

наборы решающих правил,

проверка данных с использованием колл-центра,

тестовые и валидационные выборки.
12

13. Требования международных стандартов
Standard on Automated
Valuation Models (AVMs) by International Association of Assessing Officers
2.3.3 Data Management and Quality Analysis
The reliability of any appraisal depends on accurate data. Appraisal data fall into two general categories:
property data and market data. Property data relate to location, land characteristics, and building features.
Market data include sales, income, and cost information. Asking prices and independent appraisals can
sometimes be used to supplement sparse sales data.
Computerized statistical tools used to develop AVMs afford the opportunity to screen data for missing or outofrange occurrences and inconsistencies; examples include homes with more than two fireplaces or a bilevel
home with no listed lower level living area.
Cluster Analysis - A statistical technique for grouping cases (for example, properties) based on specified variables
such as size, age, and construction quality. The objective of cluster analysis is to generate groupings that are
internally homogeneous and highly different from one another. Various cluster algorithms can be employed.
Homogeneous - Possessing the quality of being alike in nature and therefore comparable with respect to the
parts or elements; said of data if two or more sets of data seem drawn from the same population; also said of data if
the data are of the same type (that is, if counts, ranks, and measures are not all mixed together).
13

14. Этапы верификации

составление и анализ дескриптивной статистики,

анализ и отсеивание выбросов,

составление частотного словаря,

обработка регулярных выражений,

кластеризация объектов статистическими методами,

построение экспертной системы на решающих правилах,

заполнение пропущенных числовых значений с помощью
алгоритма, основанного на методе максимального
правдоподобия,

тестирование полученных результатов.
14

15. Примеры данных для верификации
Кадастровый номер
Проблемные данные
Детский сад, площадь - 0 м2,
Наименования:
:bkjq ljv
74-Б:Н-Б:КВ-2518-452
адовый домик 192
36
Количество надземных этажей:
91, 2006, 2/3
Количество подземных этажей:
56,6;
С_Д__145
Суть проблемы
Метод решения
отсутствуют принципиальные данные заполнение пропущенных
числовых значений с помощью
алгоритма, основанного на
методе максимального
правдоподобия
бессмысленные данные
обработка регулярных
выражений и экспертная
система на решающих правилах
бессмысленные данные
бессмысленные данные
Ворота, Ворота с калиткой, ворота, орфографические ошибки, разные
забор, Вороты, Воррота, ворта,
названия идентичных объектов
Забор
экспертная система на
решающих правилах
экспертная система на
решающих правилах
обработка регулярных
выражений
15

16. Примеры данных для верификации
Кадастровый номер
Проблемные данные
объект индивидуального жилищного
стрроительства
Суть проблемы
орфографическая ошибка
Метод решения
обработка регулярных
выражений
ВЛ-10кВ "ОТЭЦ-1-Багерная насосная
№2"
Назначение здания:
005001999000
нечетко идентифицирован
объект оценки
бессмысленные данные
Год постройки «n/a» и 1900
отсутствующие и
недостоверные данные
Садовый домик,
садовый домик,
садовый домик №4,
Садовый домик №88,
разные названия
идентичных объектов
экспертная система на
решающих правилах
обработка регулярных
выражений и экспертная
система на решающих
правилах
заполнение пропущенных
числовых значений с
помощью алгоритма,
основанного на методе
максимального
правдоподобия
обработка регулярных
выражений
16

17. Ошибочные кросс-секционные данные
17

18. Преимущества статистических методов верификации

единообразное решение проблем во всей базе данных с
четким описанием и обоснованием,

наличие дескриптивной статистики по генеральной
совокупности данных, позволяющее значительно повысить
эффективность моделирования,

вычисляемая статистическая точность результатов
применения методов верификации,

сокращение времени оценки и рецензирования,

повышение точности итоговых результатов,

соблюдение требований международных стандартов.
18

19. Сбор и верификация исходных данных - другие случаи
Разработка удельных показателей
инвестиционных проектов:


стоимости
реализации
исходные данные – результаты тендеров на заключение
EPC-контрактов,
проблема нормализации инженерных данных.
Fraud-score:


исходные данные для выборки – судебные решения;
проблема идентификации юридических и физических лиц.
19

20. Выбор факторов
Y(стоимость или
ставка)
Y (стоимость
или ставка)
Х1 (выручка)
Х2 (чистые активы)
1
Х1 (выручка)
Х2 (чистые
активы)
1
1
Требования к факторам:
 значимость: 1, 2 > 0,7;
 независимость: 3 < 0,4;
 экономическая интерпретация.
20

21. Построение модели. Линейная регрессия.
24.00
22.00
20.00
18.00
16.00
14.00
Y
12.00
16.00
17.00
18.00
19.00
20.00
X
21.00
22.00
23.00
24.00
Карл Фридрих Гаусс
(1777-1855)
Общий случай:
Y = α+β1X1+β2X2+…+βnXn+ε
21

22. Построение модели. Проблема робастности.
1,955
12,759
23,564
34,368
45,173
55,977
66,782
77,586
88,391
99,195
above
22

23. Построение модели. Проблема робастности.
Решение – установление приоритета относительных отклонений над
абсолютными за счет логарифмического шкалирования исходных данных:
ln(Y) = α+β1ln(X1)+β2ln(X2)+…+βnln(Xn)+ε
23

24. Построение модели. Проблема мультиколлинеарности.
F2
Схема действия
метода главных
компонент
F1
F3
gF
24

25. Построение модели. Нелинейные модели.
Факторная модель в Бразилии:
пример зарубежного опыта
Зависимость между удельной стоимостью строительства
1 км воздушной линии электропередачи напряжением
69—138 кВ в тыс. долл. США (C) и еѐ мощностью в МВА (P):
C = – 0.0129666P2 +
+1.24905043P + 21.43201020
ε
25

26. Построение модели. Нейронные сети.
Модель нейрона МакКаллока-Питтса
Уоррен Маккаллок
(1898-1969)
Уолтер Питтс
(1923-1969)
Si = f(jwijSj – i)
26

27. Построение модели. Нейронные сети.
Функции активации




Входные сигналы формируются в
рецепторах. Далее эти сигналы
умножаются на веса соответствующих
синапсов, которые изменяются при
обучении, затем результаты
суммируются. На основе полученной
суммы с помощью функции активации
вычисляется выходной сигнал нейрона.
«Обучение с наставником» для задач
распознавания, когда заранее известен
правильный ответ и сеть настраивается
на выдачу ответов, максимально
приближенных к нему.
«Обучение без наставника» для задач
классификации, когда правильный ответ
неизвестен, но набор параметров
относительно устойчив и раскрытие
внутренней структуры данных или связей
между образцами.
Смешанные формы обучения.
27

28. Логистическая регрессия
Модель логистической регрессии, имеет вид:
t = w·x+b
y – значение признака в интервале [0,1];
w – весовые коэффициенты;
b – свободный член;
Оценка весовых коэффициентов производится
методом максимального правдоподобия.
ROC-кривая (англ. Receiver Operating Characteristic) –
график, позволяющий оценить качество бинарной
классификации, отображает зависимость доли верных
положительных классификаций от доли ложных
положительных классификаций при варьировании
порога решающего правила.
Количественную интерпретацию ROC даѐт показатель
AUC (англ. Area Under Curve) - площадь, ограниченная
ROC-кривой и осью доли ложных положительных
классификаций. Чем выше показатель AUC,
тем качественнее классификатор.
28

29. Построение модели. Другие модели.

CART (бинарные деревья регрессии и классификации),

нечеткая логика,

стохастические процессы.
Лотфи Заде (1921-)
Норберт Винер (1894-1964)
29

30. Получение оценок

в построенную модель подставляются данные объекта
анализа,

проводится экономическая интерпретация полученных
результатов.
30

31. Построение модели. Проверка статистической значимости.
критерий R2 и его модификации,

графический анализ,

дисперсионный анализ,

тестовые и валидационные выборки.
Остатки

-5.0000
-4.0000
-3.0000
-2.0000
6
4
2
0
-1.0000 -2
0.0000
-4
-6
-8
-10
1.0000
2.0000
3.0000
Factor
31

32. Экономические модели
32

33. Основы дисконтирования и капитализации
Pt 
CFt 1
CFt  2
CFt  n

 ... 
1  r1 1  r2 ...1  rn 
1  r1 1  r1 1  r2 
n
Стоимость актива
r=const; n→срок жизни актива
Pt  

Сумма бесконечной геометрической прогрессии
S

Стоимость актива
r=const; CF=const


Модель дисконтирования дивидендов (Dividend
discounting model, DDM) Уильямса (1938)
i 1
Et CFt  i 
1  r i
a1
1 q
Pt 
CF
r

dt
t
t 1 1  re 
Pt  
33

34. Классические модели дисконтирования

Модель оценки акций с однопериодной
доходностью

Модель дисконтирования дивидендов DDM
(модель Гордона-Шапиро, 1956);
r=const; n→∞
Pt 
d t  Pt 1
1 r

Pt  
i 1

Модель капитализации дивидендов с учетом
их нулевого роста
r=const; n→∞; d=const
Pt 

GGM (модель постоянного роста Гордона)
r=const; n→∞; g=const
Pt 

Модель капитализации денежных потоков с
учетом их постоянного роста
r=const; n→∞; g=const
Pt 
Et d t i 
1  r i
d
r
Майрон Гордон
1920-2010
d t 1  g 
rg
FCFt 1  g 
rg
34

35. Модели дисконтирования и капитализации дивидендов
Достоинства
- модели легко теоретически обосновываются, т.к. дивиденды являются ключевым
источником дохода по акциям;
- дивиденды – более подходящий измеритель денежных потоков по акциям при оценке
миноритарных пакетов, т.к. их владельцы не имеют влияния на размер и временное
распределение денежных потоков компании.
Недостатки
- не все компании (а в российской практике – далеко не все) платят дивиденды, а без
анализа исторической динамики невозможно определить будущие дивиденды;
- дивидендная политика может различаться у разных компаний (в российской практике
она часто вообще отсутствует);
- модели крайне чувствительны к изменению ставки, темпов роста и других вводных
данных, а также характеризуются значительной неопределенностью TV.
Резюме
Модели применимы, когда:
- компания платит дивиденды, причем имеется историческая динамика (минимум 5 лет);
- компании следует официально принятой дивидендной политике;
- акционеры не имеют возможности повлиять на текущую деятельность компании
(миноритарии).
35

36. Модели дисконтирования денежных потоков (DCF)
Инвестированный капитал
Собственный капитал
Денежный поток
FCFE = Net Income - (CapEx – D&A) ΔNNWC
= Net Income + D&A – CapEx ΔNNWC
re
Ставка дисконтирования
Модели капитализации
V0 
(1-стадийная модель)
n
Модели дисконтирования
(2-стадийная модель)
Термины и аббревиатуры:
ΔD
FCFF= EBIT (1 - t) – (CapEx – D&A) ΔNNWC
= EBIT (1 - t) + D&A – CapEx ΔNNWC
WACC = re x we + rd (1-t) x wd
FCFE1
re  g
FCFEt
TVn
V0  

t
1  re n
t 1 1  re 
VA0 
n
VA0  
t 1
FCFF1
WACC  g
FCFFt
TVAn

t
1  WACC  1  WACC n
Конечная
стоимость
(TV),
как
правило, определяется 3 способами:
1. По модели GGM
2. По мультипликаторам (P/E, EV/EBITDA и т.д.)
3. По остаточной балансовой стоимости
FCFE (Free Cash Flow to Equity) – свободный денежный поток на собственный капитал;
FCFF (Free Cash Flow to Firm) – свободный денежный поток фирмы
(на инвестированный капитал);
Net Income – чистая прибыль
EBIT (Earnings before interest and taxes) – прибыль до вычета налогов и процентов; t – ставка налога на прибыль
EBITDA (Earnings before interest, taxes, depreciation and amortization) – прибыль до вычета налогов, процентов износа и амортизации
D&A – износ и амортизация
CapEx (capital expenditures)– капитальные затраты
NNWC (net non-cash working capital) – чистый неденежный рабочий (оборотный) капитал, т.е. запасы + дебиторская задолженность –
кредиторская задолженность
WACC (weighted average cost of capital) – средневзвешенная стоимость капитала (инвестированного)
We и wd – доли собственного и заемного капитала в инвестированного капитале
V0 – текущая стоимость собственного (акционерного) капитала
VA0 – текущая стоимость операционных активов
Инвестированный капитал – сумма собственного капитала (E) и долга (D) на долгосрочной основе (определение из МСО)
36

37. Модели дисконтирования денежных потоков (DCF)
Достоинства
-свободные денежные потоки (FCFF или FCFE) могут быть спрогнозированы, исходя из
исторической динамики финансовых показателей, даже если компании не платят
дивиденды.
Недостатки
- иногда FCF могут оказаться отрицательными обычно из-за высоких капитальных затрат
(CapEx), особенно у компаний, находящихся на старте своей деятельности (start-up); для
преодоления этой проблемы оценщик должен построить долгосрочный прогноз
финансовых показателей компании (на 10-20 лет), но это не всегда возможно из-за
отсутствия информации о макроэкономических и отраслевых прогнозах на такой
временной горизонт;
- модели крайне чувствительны к изменению ставки, темпов роста и других вводных
данных, а также характеризуются значительной неопределенностью TV.
Резюме
Модели применимы, когда:
- компания не платит дивиденды или выплаты дивидендов исторически нестабильны при
отсутствии дивидендной политики;
- положительные FCF компании могут быть спрогнозированы в обозримом будущем;
- акционерам принадлежит контрольный пакет, и они могут повлиять на текущую
деятельность компании (мажоритарный акционер).
37

38. Теория Миллера-Модильяни


Теорема ММ №1 (1958):
стоимость компании не зависит
от структуры капитала
(финансового левериджа)
Компромиссная теория
Мертона Миллера (1976)
V V 
L
U
EBIT
r
V S
U
U
VL  S L  D
VL – стоимость левериджной фирмы (D>0)
VU – стоимость нелевериджной фирмы (D=0)
V 
U
EBIT( 1Tc )( 1Ts )
re
 ( 1T )( 1T ) 
c
s  D
VL VU  1
( 1Td )




Мертон
Миллер
1923-2000
Франко
Модильяни
1918-2003
D
I ( 1Td )
rd
Tc – налог на корпорации (налог на прибыль)
Ts – налог на личный доход от владения
акциями
Td – налог на личный доход от владения
облигациями
I – выплаченные проценты по долгу
Если (1 – Tc) (1 - Ts) = 1 – Td, то VL = VU
38

39. Эффект налогового щита
Firm U
Прибыль до выплаты
налогов и процентов
Interest
Процентные платежи по
долгу
Taxable income
Прибыль до
налогообложения
Profit Tax (24%)
1000
1000
0
300
1000
700
240
EBIT
Firm L
168
Налог на прибыль (24 %)
Net income after tax
Чистая прибыль после
уплаты налогов
760
532
Cash flow available for all
security holders
Денежный поток,
доступный для всех
держателей ценных бумаг
760
832
39

40. Экономические модели
Недостатки классических моделей дисконтирования

Сомнительные расчеты будущих дивидендов, чистой прибыли и денежных потоков

Ограничения по значению ставки (r>g в моделях постоянного роста)

Высокая чувствительность к изменению ставки дисконтирования

Невозможность оценивать убыточные компании
40

41. Модели остаточного дохода
Оценка остаточного дохода (residual income value - RIV) строится на индикаторах
стоимости, отражающих ее изменение посредством сравнения прибыли или денежных
потоков компании с нормированными доходами

EVATM (Economic Value Added) –
экономическая добавленная стоимость – Stern
& Stewart; Economic Profit Model – McKinsey
EVAt  NOPLAT t  IC t 1  WACC 
( ROIC  WACC )  IC t 1

MVA (Market Value Added) – рыночная
добавленная стоимость
MVA  MV  IC

SVA (Shareholder’s Value Added) –
добавленная стоимость для акционеров ALCARTM Alfred Rappaport
SVA  NOPAT WACC

CFROI (Cash Flow Return On Investment) – Holt
Value Associates; CVA (Cash Value Added) –
Boston Consulting Group)

EBM (Expectation Based Management)
n
CFi
TVn 1

i
1  r n1
1
i 1   r 
r  CFROI; CFROI WACC
IС  
EBM  EVA fact  EVAexp
41

42. Собственный капитал
RI = NI – re x BV = (ROE – re) BV
EVA = NOPLAT – WACC x IC = (ROIC – WACC) IC
re
Денежный поток
Инвестированный капитал
WACC = re x we + rd (1-t) x wd
Ставка дисконтирования
Модели капитализации
(1-стадийная модель)
Модели дисконтирования
(2-стадийная модель)
Термины и аббревиатуры:
ROE  re  BV
 ROE  re 

 BV0 1 

re  g
re  g 


n
RIt
RI / r  g 
V0  BV0  
 n 1 e n
t
1  re 
1
t 1   re 
V0  BV0 
0
RIt
TVn  BVn
 BV0  

t
1  re n
1
t 1   re 
n
ROIC  WACC IC
 ROIC  WACC 

 IC0 1 

WACC  g
WACC  g 


n
EVA
EVAn 1 / WACC  g 
t
VA0  IC0  

t
1  WACC n
1
t 1   WACC 
VA0  IC0 
n
 IC0  
t 1
0
EVA
TVAn  ICn
t

1  WACC t 1  WACC n
Конечная стоимость (TV), как правило, определяется 3
способами:
1. По модели GGM (предполагая, что ROE/ROIC стремятся
к нормализованному значению
2. По мультипликаторам (P/B, EV/IC)
3. Приравнивается к BVn, исходя из предположения RIn=0
(ROEn=re)
NI (Net Income) – чистая прибыль
NOPLAT (Net Operating profit less adjusted taxes) = EBIT (1-t)
BV (Book Value)– балансовая стоимость собственного капитала
IC (Invested Capital) балансовая стоимость инвестированного капитала
ROE – рентабельность собственного капитала
ROIC – рентабельность инвестированного капитала
V0 – текущая стоимость собственного (акционерного) капитала
VA0 – текущая стоимость инвестированного капитала (операционных активов)
Инвестированный капитал – сумма собственного капитала (E) и долга (D) на долгосрочной основе (определение из МСО)
Остаточный доход (residual income) = экономическая прибыль (Economic profit) = аномальные доходы (abnormal earnings)
RIM – прямое следствие DDM!
Ключевая
предпосылка
–
выполнение равенства чистого
прироста
(clean
surplus
relation, CSR), т.е. BV1 = BV0 +
NI1 – d1
42

43. Модель Эдвардса-Белла 1928, 1961
Первоначальные предпосылки:
Модель DDM
1

dt
V0  
t
t 1 1  re 
2
Соотношение чистого
прироста (clean surplus
relation, CSR):
BVt = BVt-1 + NIt – dt
3
Остаточные доходы
(«аномальные» доходы):
RIt = NIt – re x BVt-1 =
=(ROEt – re) BVt-1
Выразим чистую прибыль из второго соотношения и подставим в третье равенство, а затем выразим из него дивиденды:
NIt = BVt - BVt-1 + dt
RIt = BVt - BVt-1 + dt – re x BVt-1
dt = (1+re) x BVt-1 + Rit – BVt
Далее подставляем получившееся выражение в модель DDM:
V0 
1  re BV0  RI1  BV1  1  re BV1  RI 2  BV2  ...  1  re BV 1  RI   BV
1  re 
1  re 2
1  re 
Отсюда после взаимного сокращения членов и допущения, что член BV∞/(1+re)∞ близок к нулю,
получаем модель Эдвардса-Белла:

V0  BV0  
t 1
RIt
1  re t
Нереалистичное
предположение!!!
Если предположить, что существует постоянный темп прироста «аномальных доходов» g, тогда:
ROE1  re  BV
RI1
V0  BV0 
 BV0 
0
re  g
re  g
Если ROE > re, то V0 > BV0
Если ROE < re, то V0 < BV0
Если ROE = re, то V0 = BV0
43

44. Линейная информационная динамика - вклад Ольсона
Ольсон (James Ohlson, 1995) предположил,
что «аномальные доходы» изменяются во времени согласно следующим авторегрессионным процессам:
ID1 : RIt 1  RIt  t   t 1
ID2 : t 1   t  t 1
0   1
0   1
Переменная v представляет собой фактор «прочей информации» о той части аномальных прибылей следующего
года, которая не представлена в текущих аномальных доходах:
vt  RI t 1  RI t
Показатели ω и γ представляют собой индексы роста для переменных RI и v, причем этот рост отрицательный (!), т.к.
ω=(1+g)≤1, т.е. g ≤ 0.
В целом, это соответствует экономической теории в части выравнивания доходов к средней величине (т.е. стремления
аномальных доходов к 0).
44

45. Модель EBO (Edwards, Bell, Ohlson, 1961,1995)
Соединив линейную информационную динамику Ольсона и модель Эдвардса-Белла, получим:

V0  BV0  
t 1
RIt
RI0  v0  RI0  v0   v0   (RI0  v0 )  v0    2v0
 BV0 


 ... 
1 r
1  r t
1  r 2
1  r 3
 1

    2     2
BV0  RI0 
v0 


 ...
t
 1  r 1  r 2

1  r 3
1
t 1   r 



t
Сгруппировав слагаемые, относящиеся к RI и v, и выразив α1 и α2 как суммы бесконечно убывающих геометрических
прогрессий, получаем формулу модели EBO:
Vo  BVo  1RI0   2 0
1 

1 re 
2 
1 re
 1 re   1 re  
Эмпирические
исследования
Дечоу,
Хаттона
и
Слоана
(Dechow, Hutton, Sloan, 1999), провод
ившиеся на основе статистической
выборки более 50 000 компаний США
за
период
1976-1995
гг., показали, что:
ω = 0,62
γ = 0,32
• Если ω и γ равны 0, то аномальных доходов в будущем не предполагается и их текущая стоимость равна 0 (стоимость
собственного капитала V0 при этом равна балансовой стоимости)
• Если ω равна 1, то аномальных доходы в будущем существуют перманентно на текущем уровне и стоимость
собственного капитала V0 = BV0 + RI0/re
45

46. Входные данные для модели EBO
Vo  BVo  1 RI 0   2 0  BVo  1 RI 0   2 RI1  RI 0 
Vo  BVo   2 RI1   2  1 RI 0
Для определения стоимости собственного капитала по модели EBO необходимы следующие данные:
1. Балансовая стоимость собственного капитала на конец текущего периода BV0
2. Балансовая стоимость собственного капитала на конец предыдущего периода BV-1 (для расчета RI0)
3. Чистая прибыль за последний год NI0 (для расчета RI0)
4. Ожидаемая чистая прибыль в следующем году NI1 (для расчета RI1)
5. Ставка дисконтирования – стоимость собственного капитала re
6. Значение параметров авторегрессии ω и γ
Взаимосвязь модели EBO с мультипликатором P/BV

BV1 
P0 / BVo  1   2 ROE1  re    2  1  ROE0  re

BV0 

Таким образом мультипликатор P/BV будет больше 1, когда ROE будет больше re!
Взаимосвязь с P/BV
классической
модели капитализации
остаточных доходов:
P0
ROE  re
 1
BV0
re  g
46

47. Достоинства и недостатки модели EBO
Достоинства
- Модель представляет собой гармоничное сочетание затратного (поскольку задействован балансовый собственный
капитал) и доходного подходов (так как в расчетах применяется текущая и ожидаемая чистая прибыль)
- Модель «раньше признает» стоимость, чем DDM и FCF, благодаря BV и за счет этого результат расчета по модели
менее чувствителен к изменению ставки дисконтирования и других вводных данных и в меньшей степени зависят от
неопределенности будущих ожидаемых доходов (преимущество перед DDM и FCF)
- Модель позволяет дать наглядную и прозрачную трактовку стоимости через механизм остаточных («аномальных»)
доходов: если компания использует собственный капитала эффективно (ROE>re), то стоимость собственного капитала
компании выше его балансовой стоимости и наоборот
Недостатки
- Модель требуют детального анализа и корректировок финансовой отчетности, особенного в части оценки по
справедливой рыночной стоимости активов и пассивов (характерно для российской практики, если компания не
применяет МСФО). Частично этот недостаток устраняется механизмом, заложенным в саму модель – чем ниже BV, тем
выше ROE
- Модель предполагает выполнение соотношение чистого прироста (clean surplus relation), что на практике далеко не
всегда так (особенно в случае с РСБУ)
- Исчерпывающий тест модели и расчет параметров ω и γ сделан пока только по рынку США
- Модель не позволяет оценивать компании с отрицательным собственным капиталом
47

48. Модель FOM (Feltham-Ohlson, 1998)
Ключевое отличие модели FOM от модели EBO: соотношение чистого прироста не
выполняется, т.е. собственный капитал может пополняться за счет иных источников, помимо
чистой прибыли
Линейная информационная динамику Фелтхама-Ольсона:
RIt 1  RIt  1 BVt  1t   1t
 2 BVt  2t   2t
 1 1t  1t
BVt 1 
 1t 1 
 2 t 1 
 2 2t   2t
Джеймс Ольсон
1943-
1 ,  2  1 0    1
1  0
1  2  1 r
Соединяя модель Эдвардса-Белла с линейной информационной динамикой Фелтхама-Ольсона, получим:
V0  BV0  1 RI0   2 BV0  1 1t   2 2t
1 
2 

1 r 
1 
1 (1 r )
1 r
 1 r   1 r  1 
 r 1 1 r  2 
2 
2
1 r  2
Эмпирические
тесты
показали
низкую
статистическую значимость модели!
48

49. Модель Рисса (1999)

 1 g 
rw 
V0  BV0 1  e   NI 0 
 r g
 r  g w 

e


 e

 NI 1  g   re BV0 
 BV0   0
w
re  g


где w – весовой коэффициент для чистой прибыли (от 0 до 1)
Эмпирический тест модели был проведен в 2001 году на основе данных около 1100 компаний
финансового сектора (коммерческие банки, страховые компании, инвестиционных компаний и
агентства недвижимости) из 6 европейских стран за период 1989-2000 гг.
Результаты анализа показали, что значение параметра w и статистическая значимость
модели в значительной степени зависит от cабсектора (sub-sector) финансовой отрасли, а также
страны и принятой в ней традиции создания стоимости – shareholder’s value vs. stakeholder value.
49

50. Стохастические модели
50

51. Модель Бакши-Ченга
 m 

Pt    M t 
D d
 mt 

t

 P(t) – стоимость оцениваемой акции в момент t
 Мt [.] – математическое ожидание в момент t
 τ = t + Δt
 m(τ)/m(t) – ценовое ядро, представляющее собой
отношение мгновенной будущей и текущей
стоимости денег
 D(τ) – дивидендный поток в момент τ
51

52. Агрегационная теорема Типпета-Кука-Эштона
   i(τ  t)
dτ 
Pt   b(t)  M   e
a(τ ) 
t 
 
t

 P(t) – стоимость оцениваемой акции в момент t
 Мt [.] – математическое ожидание в момент t
 i(.) – стоимость капитала компании
 a(τ) – сверхдоходы в момент τ
52

53. Модель Адама



* Независимость economic value от параметров финансового рынка. Economic value
от привлечения новых клиентов не будет зависеть от состояния финансового
рынка на дату заключения договора.
Следствие: компания одинаково приращивает стоимость в условиях как высоких,
так и низких ставок.
Economic value соответствует функции приведенного дохода, полученного от
существующих клиентов

  r ( s ).ds 
t
EV  E   Incometstock .e
horizon t



0




В соответствии с пунктом *, ожидаемая сумма приведенных доходов, полученных
от новых клиентов не чувствительна к изменениям финансовых рынков

  r ( s ).ds 
new production

  Constant
E  Incomet
.e 0
t
horizon t





t

Следовательно, нечувствительность ожидаемых будущих доходов к движениям
финансового рынка делает economic value нечувствительной к движениям
финансового рынка. Другими словами при высокоразвитом уровне моделирования,
возможно согласовать в одной модели показатели чувствительности и показатели
основанные на разнице процентных ставок, такие, как экономический капитал

 r ( s ).ds 
Incomestock  new production .e 

0
dEV   dE
t


horizon t




t
53

54. Вспомогательные модели
54

55. Модели стоимости капитала
Ставка дисконтирования (стоимость капитала, Cost of Capital) – это:
-
требуемая норма доходности (required rate of return) всеми поставщиками (источниками)
капитала как компенсация за пользование их средствами с учетом риска инвестирования.
-
альтернативная стоимость капитала для его поставщиков (opportunity cost of funds for the
suppliers of capital)
Источники капитала компаний:
1) Обыкновенные акции;
2) Привилегированные акции;
3) Заемные средства (кредиты и займы, облигации и т.д.)
4) Прочие (конвертируемые облигации и пр.)
Стоимость капитала (истоки) – откуда берется значение ставки?
•
Стоимость долга rd
- спросить у банка!
•
Стоимость собственного капитала re
- спросить у акционеров!
55

56. Средневзвешенная стоимость капитала (WACC)
WACC = re x we + rd (1-t) x wd
где:

rd - стоимость долга

re - стоимость собственного капитала

t – ставка налога на прибыль

we и wd – доли собственного и заемного капитала в инвестированного капитале
Расчет весов (we и wd) в формуле WACC производится одним из следующих способов:
1) идеальная ситуация, когда применена целевая (target) структура капитала, т.е. пропорции долга (Debt, D) и
собственного капитала (Equity, E), которые компания стремиться достичь (НО! далеко не все компании раскрывают, а
иногда просто не имеют такой информации)
2) Текущая структура капитала принимается за целевую (маловероятная ситуация!)
3) Среднеотраслевая структура капитала принимается за целевую (или в прогнозном периоде предусматривается
стремление текущей структуры к среднеотраслевой)
Идеально, если при расчете весов (we и wd) использована рыночная стоимость собственного капитала и долга (однако
такая информация далеко не всегда имеется!)
Стоимость долга (rd) определяется исходя из кредитной ставки (если кредит выдан на рыночных условиях) и/или
доходности к погашению (YTM) облигаций компании
rd (1-t) – посленалоговая стоимость долга (с учетом эффекта налогового щита)
56

57. Модель ценообразования по капитальным активам (CAPM)
ri  rf   i rm  rf   rf   i ERP
где:
• ri – ожидаемая ставка доходности i-го актива
• rf – безрисковая ставка доходности
• rm – ожидаемая рыночная ставка доходности (рыночного
портфеля)
• ERP (Equity Risk Premium) или MRP (market risk premium) –
премия за риск инвестирования в собственный капитал (разница
между рыночной доходностью rm и безрисковой rf)
• βi – мера систематического риска для i-того актива (показывает
чувствительность доходности i-того актива к изменению
доходности рыночного портфеля)
•ставка, свободная от риска
дефолта;
•доходность
по
гос.
облигациям
(не
всегда
свободны от риска дефолта!)
i 
covri ; rm 

  i ,m i
 2 rm 
m
ri  i  i rm   i
• если β>1, то актив более доходный, чем рынок;
• если β<1, то актив менее доходный, чем рынок;
• если β=1, то доходности актива и рынка равны.
История модели:
• разработана Джеком Трейнером (Jack Treynor, 1962), Уильямом Шарпом (William Sharpe, 1964), Джоном Литнером (John
Lintner, 1965) и Яном Моссином (Jan Mossin, 1966) независимо друг от друга.
• строится на «Теории портфеля» Гарри Марковитца (Harry Markowitz, 1952) и является частью «Теории рынка капитала»
(Capital Market Theory, CMT).
Предпосылки модели (нереалистичные!):
1. На рынке капитала существует большое количество частных (небольших) инвесторов
2. Все инвесторы имеют одинаковый временной горизонт
3. Инвесторы могут вкладывать только в ценные бумаги, торгуемые на открытом рынке
4. Инвесторы занимают и дают в долг под одну и ту же номинальную безрисковую ставку
5. Налоги и транзакционные издержки отсутствуют
6. Все инвесторы рациональны и оптимально диверсифицируют свой портфель
7. Вся информация доступна всем инвесторам в одно и то же время и все инвесторы имеют одинаковые ожидания
57

58. Проблемы и недостатки CAPM
1. Безрисковая ставка доходности

доходность по гос. облигациям брать краткосрочную или долгосрочную?

доходность по гос. бумагам далеко не всегда свободны от риска дефолта!
2. ERP (премия за риск инвестирования в собственный капитал)

что считать рынком?

за какой исторический период делать расчет? арифметическая или геометрическая
средняя? от краткосрочной или долгосрочной безрисковой ставки?
3. Коэффициент β

за какой исторический период следует считать бету?

что делать, если история котировок акций компании очень недолгая (и/или гораздо
ниже, чем история индекса)?

что делать с акциями непубличных компаний?
Решение 1
Применяются различные варианты расчета β:
1) Потребительские (регрессия прироста
прибыли против прироста ВВП – страны
или мира)
2) Бухгалтерские
(регрессия
прироста
бухгалтерской чистой прибыли против
рыночного индекса
3) Скорректированные
и др.
Решение 2
Применение отраслевых β, рассчитанных исходя из
данных о публичных аналогах.
Это осуществляется при помощи поправки Хамады (Robert
Hamada, 1972)
Последовательность:
1) Рыночные (левериджные) беты (βL) компанийаналогов (или отрасли) с помощью данной формулы
«очищаются» от финансового рычага (D/E) и
рассчитывается среднее значение нелевериджной
беты отрасли (βU)
2) Нелевериджная бета отрасли (βU) по той же формуле
корректируется на финансовый рычаг оцениваемой
компании
ERP рассчитывают как от
Treasury Bills (краткосрочных
облигаций), так и от Treasury
Bonds (долгосрочных)
Доходность рынка в целом
считается от индексов:
• Dow Jones (DJIA) с 1896
• S&P500 с 1957
• MSCI World 1500 с 1969
• Willshire 5000 с 1974
и др.
Источники по историческим бетам
платные:
• Morningstar (Ibbotson SBBI)
• COMPUSTAT (S&P)
• Bloomberg
• DataStream
• BARRA
• Value Line
• Reuters
• Hoover’s
• CorporateInformation
• Factiva
и др.
бесплатный:
• www.damodaran.com
58

59. Другие модели расчета ставки. Развитие CAPM
Теория арбитражного ценообразования
(Arbitrage Pricing Theory, APT)
3-х факторная модель Фамы-Френча
(Eugene Fama&Kenneth French, 1992)
Метод кумулятивного построения
(Build-Up Method)
ri  rf   i RP1   i RP2  ...   i RPk
ri  rf   i ERP   i SMB   i HML
• многофакторная модель (CAPM и модель ФамыФренча – частные случаи)
• большое
количество
макроэкономических,
отраслевых
и
специфических факторов
• Примеры:
1) модель
BARRA
(около
70
факторов)
предложена Барром Розенбергом в 1982 году не публичная!
2) Модель BIRR (5 факторов) предложена
Бурмейстером, Роллом и Россом в 1994 году
• SMB (small minus big) – премия за размер
(малую капитализацию)
• HML (high minus low) – премия за разное
соотношение
book-to-market
(обратное
показателю P/B)
ri = Безрисковая ставка
+ Премия за страновой риск
+ ERP
Отраслевая премия
Премия за размер
+ Премия за специфический риск
компании
1. Безрисковая ставка берется, как правило, для
США, поэтому в российских условиях к ней
необходимо добавить премию за страновой
риск или риск дефолта (Источники: мировые
рейтинговые агентства Moody’s, S&P, Fitch)
2. Источники
данных
(платные)
по
систематическим рискам (ERP, премия за
размер) и отраслевой премии:
• Morningstar (Ibbotson SBBI)
• Duff & Phelps' Risk Premium Report
Вильям Шарп
1938-
Юджин Фама
1939-
3. Публикуемых
данных
по
премиям
за
специфический риск не существует, она
определяется экспертно, поэтому основной
недостаток метода – субъективность!
Ключевые факторы, влияющие на премию за
специфический
риск
(как
правило,
экспертная балльная оценка):
• зависимость от ключевых потребителей;
• зависимость от ключевых поставщиков;
• зависимость от ключевых сотрудников;
• уровень корпоративного управления.
59

60. Скорректированная CAPM (для развивающихся рынков)
riRUS  rf RUS   i ERPUS
 RUS
 RPSMB  RPSPECIFIC
 US
ERP для
России!
где:
•
ri RUS – ожидаемая ставка доходности i-го актива в России
•
rf RUS – безрисковая ставка доходности для РФ – доходность к погашению 30-летних ОФЗ (в ней уже
заложен спрэд дефолта)
•
βi – отраслевая нелевериджная бета, скорректированная на финансовый рычаг оцениваемой
компании (проекта)
•
ERPUS – премия за риск инвестирования в собственный капитал для рынка США (например, по
историческим значениям индекса S&P500 и доходностью долгосрочных американских облигаций)
•
σRUS – стандартное отклонение рынка акций России (например, по индексу РТС)
•
σUS – стандартное отклонение рынка акций США (например, по индексу S&P500)
•
σRUS / σUS – коэффициент волатильности
•
RPSMB – премия за размер
•
RPSPECIFIC - премия за специфический риск компании
60

61. Модели оценки и мониторинга активов
активы
земля
недвижимость
бизнес
прочие
61

62. Потребители системы мониторинга
• государство
–
система
управления
государственным
имуществом, налогообложение, кадастровая оценка,
• банки – система мониторинга стоимости залогов и кредитов,
• крупные холдинговые структуры, контроль стоимости дочерних
обществ и ключевых ценообразующих активов, отчетность по
МСФО
• правоохранительные органы, противодействие коррупции и
рейдерству
62

63. Мониторинг недвижимости
63

64. Массовая оценка недвижимости
64

65. 65

66. Сводная таблица
После
задания
параметров
поиска
формируется сводная
таблица по активам
(залогам)
для
выбранного заемщика
График залоговой и
расчетной стоимостей для
выбранного актива за
заданный период времени
Статистические и
аналитические
показатели
66

67. Для данного объекта мониторинга на выбранном
интервале времени мы наблюдаем обесценение залога:
залоговая стоимость > расчетной стоимости
67

68. Сравнительная оценка
объекта мониторинга с
рыночными аналогами
Карта с местоположением
объекта и его аналогов
Основные характеристики
объекта мониторинга
68

69. Возможности системы мониторинга:

оценка стоимости различных активов в режиме реального
времени с учѐтом превалирующей рыночной конъюнктуры,

отслеживание динамики изменения стоимости во времени
как отдельно взятого актива, так и портфеля активов,

проведение сравнительного анализа активов с их
рыночными аналогами,

получение различных статистических и аналитических
параметров для отдельно взятых активов и портфелей
активов,

мониторинг стоимости залогов в режиме реального времени
и предупреждение об их обесценении.
69

70. Учет неопределенности. Опционы.

Опцион - производный финансовый биржевой инструмент (дериватив),
предоставляющий ПРАВО (НО НЕ ОБЯЗАТЕЛЬСТВО) его владельцу на покупку (или
на продажу) базового актива по заранее оговоренной цене в заранее оговоренный
срок до даты исполнения

Опцион на покупку – call option

Опцион на продажу – put option

Цена (премия) опциона – option premium
Различают:

Европейские опционы (исполняется только на дату исполнения)

Американский опцион (может быть исполнен в любой день до даты исполнения)
70

71. Принятые обозначения

S – текущая цена базового актива на рынке – spot price

X – цена исполнения опциона – strike price

T – дата исполнения опциона – expiration date (t – срок до даты
исполнения)

r – ставка безрискового вложения

с – цена опциона call

p – цена опциона put
71

72. Свойства опционов

Внутренняя стоимость опциона (intrinsic value of an
option) – ценность опциона, если бы он был
немедленно реализован
Внутренняя стоимость опциона
Тип


При деньгах (in the money), когда цена выше 0 (c>0,
p>0)

Без выигрыша, по текущей цене (at the money),
когда цена примерно равна 0
S>X
c=
0
S-X
Put
Без денег (out of money или deep out of money),
когда цена опциона равна 0 (c=0, p=0)
S<X
Call
Опционы могут быть:
Стоимость
p=
X-S
0
Предельные значения цен опционов

Принцип отсутствия арбитража –невозможности
получения прибыли из-за разницы цен на один и тот
же актив на разных рынках

Теорема о соотношении премий (цен) опционов:
Стоимость
min
Max
Call
Ценообразование опционов:
Тип
c
S-X/(1+r)
S
Put
p
X/(1+r)-S
X/(1+r)
p + S = c + X/(1+r)
72

73. Цены опционов
Call-опцион (покупатель)
X
Put-опцион (покупатель)
S
c
X
S
p
Call-опцион (продавец)
c
S
X
Put-опцион (продавец)
p
S
X
73

74. Биномиальная модель опционного ценообразования
c = HS - B
BOPM,1976 (Cox, Ross, Rubinstein – CRR)
Условия модели:

Цены на базовый актив изменяется дискретно согласно биномиальному процессу

Создание безрискового портфеля из комбинации инвестиций в акции и опционы на
эти акции

Существует безрисковая ставка вложения средств r и она постоянна

H – «дельта» опциона, коэффициент хеджирования (отображает количество акций
на один опцион, которые нужно купить для создания безрискового портфеля)

B – приведенная текущая стоимость займа
74

75. Биномиальные деревья
75

76. Модель Блэка-Шоулза,1973 (для опциона call)
c  S e -yt N(d1 ) - X e -rt N(d2 )

ln
d
Условия модели:
d
1
2

S
X

( r  y 

 d
1
 
2
2
)t
t
t

Базовый актив имеет непрерывно изменяющиеся рыночные цены

σ2 –дисперсия (вариация, волатильность) цен базового актива постоянна

Существует безрисковая ставка вложения средств r и она постоянна

Исполнение опциона немедленное

Предполагается, что стандартизованные переменные d1 и d2 нормально
распределены
76

77. Модель Блэка-Шоулза (для опциона put)
p  X e -rt N(-d 2 ) - S e -yt N(-d 1 )
Цена call – c
Факторы стоимости опциона:
Цена put – p

S – цена базового актива (spot)
↑

↑
↓

X – цена исполнения (strike)
↑

↓
↑

σ2– вариация цен базового актива
↑

↑
↑

t – время исполнения
↑

↑
↑

r – безрисковая ставка
↑

↑
↓

y – дивидендная доходность
↑

↓
↑
Майрон Шоулз 1941-
Фишер Блэк 1938-1995
77

78. Реальные опционы

Реальные опционы – различные экономические ситуации, связанные с
неопределенностью и повышенным риском и подпадающие под процесс
ценообразования опционов
Ситуации:

Инвестиционные проекты (в т.ч. в сфере недвижимости)

Оценка проблемных предприятий и банков

Оценка стартапов

Разработка полезных ископаемых

Выпуск конвертируемых ценных бумаг

Оценка патентов и др.
78

79. Реальные опционы
Опционы на стороне активов:

Опцион на прекращение деятельности (отказ от проекта) – соответствует опциону put

Опцион на отсрочку развития (на выжидание) – call

Опцион на расширение (на продолжение инвестиций) – call

Опцион на сокращение (на прекращение инвестиций) – put

Опцион на смену деятельности – call
Опционы на стороне обязательств:

Варранты – call

Конвертируемые ценные бумаги (облигации и другие долговые обязательства) - call
79

80. Факторы стоимости для реальных опционов
Факторы
Интерпретация

Цена базового актива

Текущая стоимость прогнозируемых
денежных потоков от проекта

Цена исполнения

Необходимые затраты, связанные с
проектом

Дисперсия по доходам от
аналогичных активов
компании, полученная
моделированием бюджета

Вариация цен базового актива

Срок до даты исполнения

Срок действия опциона

Дивидендная доходность

Стоимость отсрочки (годовая
стоимость отсрочки равна 1/n, где n
– срок проекта)
80

81. Оценка проблемных компаний с помощью реальных опционов
X - стоимость
непогашенных
долгов
S - стоимость активов
81

82. Оценка опциона отложенного проекта
X – начальные
затраты
S – PV ожидаемых денежных
потоков по проекту
82

83. Оценка опциона на отказ от проекта
Х - плата за
отказ от
проекта
S – PV ожидаемых
денежных потоков
83

84. Ограничения использования реальных опционов

Базовый актив, лежащий в основе реального опциона, часто не имеет рыночных
цен, поскольку не торгуется на свободном рынке

Изменение цены базового активы не является непрерывным

Дисперсию сложно рассчитать и она не всегда постоянна

Исполнение опциона может не быть одномоментным

Некоторые реальные опционы создают другие опционы (составные опционы)
84

85. Кейсы
85

86. Удельные показатели стоимости энергетического строительства
Назначение системы
Прогнозирование величины затрат на работы
и оборудование при новом строительстве или
полномасштабной реконструкции подстанций
и воздушных линий электропередачи классом
напряжения от 220 кВ
86

87. Цели создания системы
Планирование и бюджетирование
Первоначальное определение затрат на этапе средне-срочной
инвестиционной программы
Тендерная и закупочная деятельность
•Определение
предельной начальной цены при объявлении
конкурса на строительство или реконструкцию
•Контроль
экономической обоснованности заявок участников
Институциональные преимущества
Рост прозрачности и эффективности взаимодействия между ОАО
«ФСК ЕЭС», подрядчиками, государственными финансовоконтрольными органами, стратегическими инвесторами
87

88. Подходы к определению стоимости строительства и реконструкции
Классическая модель
• Расчет на основе сметных показателей в базовых ценах
•
Индексация к текущим ценам
Факторная модель
• Статистический анализ фактических данных по стоимости
строительства
•
Расчѐт на основе моделей множественной регрессии
•
Применяется в США, Южной Америке, других регионах
Впервые применена ООО «Институт управления стоимостью»
в российской электроэнергетической отрасли
•
Инвестиционная модель
Расчет на основе тарифов на транспортировку электроэнергии
и инвестиционной потребности отрасли
• Применяется в США и Европе
•
88

89. Достоинства и недостатки моделей
Характеристика
Классическая
Факторная
Инвестиционная
К индексам
цен
К фактическим
стоимостным
данным
К прогнозам в
электроэнергетике
Оперативная обновляемость
Простота и скорость применения
Сценарный анализ облика объекта
Объективность оценок
Интегрируемость с
информационными системами
Работа в условиях системы RAB
Чувствительность к исходным
данным
Применимость моделей:
Прогнозирование и планирование
Стартовые цены тендеров
Финансовый контроль
89

90. Общая стоимость подстанции
Дополнительные затраты
Силовые трансформаторы
6-110кВ и здания
Прочие затраты
Базовая стоимость
Постоянный член и надбавка,
пропорциональная базовой
стоимости
Затраты на РУ, ТГ и ШР
Стоимость
подстанции
90

91. Направления дальнейшего развития системы
Автоматизация и информационная поддержка
•
Интеграция с КИСУ «Закупки» и базой данных по оборудованию
Создание баз данных по удельным стоимостям отдельных элементов
подстанций
•
•
Интеграция с электронной площадкой ТЗС «Электра»
•
Оперативная актуализация моделей в полуавтоматическом режиме
Создание прозрачного механизма расчёта стоимости, единого для
заказчика и подрядчиков
•
Внедрение RAB
• Разработка инструмента для прогнозирования изменения тарифов в результате
осуществления инвестиционной программы при внедрении RAB (системы
формирования тарифа по принципу возврата доходности на вложенный капитал)
Совершенствование моделей
• Расширение выборки исходных данных и множества учитываемых факторов
• Учёт надёжности оборудования и определение оптимального соотношения
«стоимость / надёжность»
91

92. Пул моделей
Модели стоимости
строительства и
реконструкции
Для различных
наборов факторов
Для различных
элементов затрат
Для различных типов
затрат
От минимального
набора наиболее
важных характеристик
до подробного
описания объекта
По наиболее важным
видам оборудования
и по главам сметы
Отдельно для
стоимости работ и
оборудования, либо
все затраты суммарно
92

93. Индекс должной осмотрительности ИДО СПАРК-Интерфакс

Система может стать эффективным инструментом экспрессдиагностики

Внедрение системы позволит выявить неблагонадежные компании и
исключить их из выборки, что позволит адекватно рассчитывать
среднеотраслевые коэффициенты

Формирование адекватного информационного обеспечения для
использования в построении финансовых моделей
(среднеотраслевые уровни рентабельности, собственного
оборотного капитала и др.)
93

94. База данных СПАРК на момент моделирования Индекса

7,3 миллиона компаний в базе данных СПАРК (включая ликвидированные)

4,6 миллиона компаний (включая ликвидированные) имеют организационно-правовую
форму обществ с ограниченной ответственностью

По 35% ООО в СПАРК представлена отчетность хотя бы за один год из последних трех лет

Компании, сдающие отчетность в соответствии с МСФО, составляют 0,0124% от общего
количества компаний в СПАРК

В базе данных насчитывается 0,0047% системообразующих компаний

В базе данных насчитывается 0,003% стратегических предприятий

Российские компании-эмитенты, представленные в базе СПАРК, составляют 0,0544% от
общего количества всех компаний базы

0,0078% базы данных СПАРК - это члены Российского союза промышленников и
предпринимателей
94

95. Пример применения Индекса анализ в отрасли «Розничная торговля»
95

96. Предсказание банкротства – история и современность
1-й этап исследований по предсказанию банкротств 1930 – 1965:

1930 - Bureau of Business Research (BBR) 24 фактора/ 29 фирм выборка;

1935 - Smith and Winakor 6 факторов/183 фирмы выборка.
Мало данных, мало факторов, простейшие модели.
2-й этап исследований по предсказанию банкротств 1965 – наши дни:

1966 - Beaver 30 факторов/79*2 фирмы выборка;

1968 - Altman 5 факторов/100 000 фирм выборка.
Первые компьютерные модели, больше выборки, больше факторов, сложнее модели.
3-й этап исследований по предсказанию банкротств:
Использование открытых данных, колоссальные выборки; сложные модели, включая
SVM и нейронные сети.
96

97. Факторное пространство (коэффициенты для модели)
коэффициент
'Net Income/Total Assets'
'Current assets/Current liabilities'
'Working capital/Total assets'
'Retained earnings / Total assets'
'Earnings before interest and taxes / Total assets'
'Sales / Total assets'
'Quick ratio'
'Total debt / Total assets'
'Current assets / Total assets'
'Net income / Net worth'
'Cash / Total assets'
'Quick assets / Total assets'
'Current assets / Sales'
'Inventory / Sales'
'Operating income / Total assets'
'Net income / Sales'
'Long-term debt / Total assets'
'Net worth / Total assets'
'Total liabilities / Net worth'
'Cash / Current liabilities'
97

98. Спасибо за внимание!
98