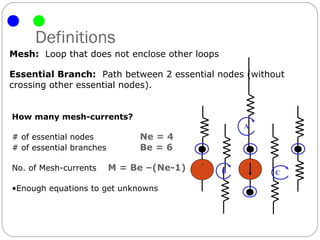
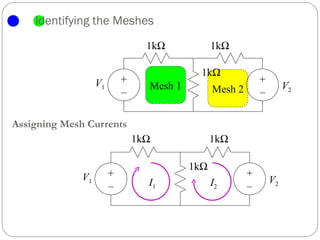
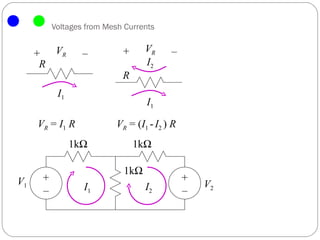
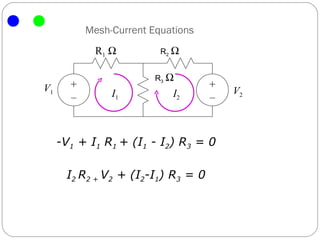
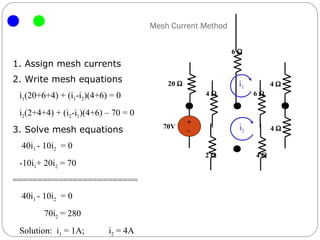
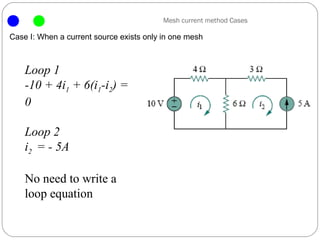
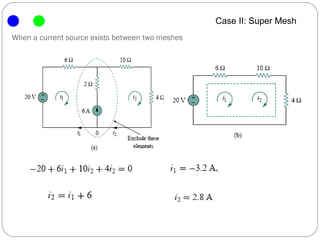
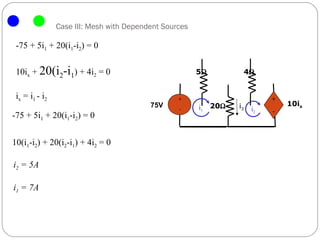
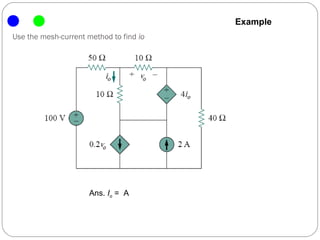
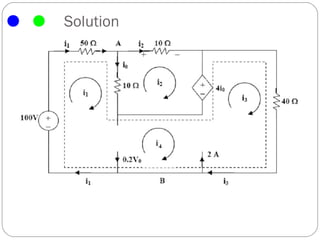
The document introduces the mesh-current method for solving electric circuits. It defines key terms like mesh and essential branch. The steps of the mesh-current method are: 1) identify meshes, 2) assign a current to each mesh, 3) write Kirchhoff's voltage law equations for each mesh in terms of the mesh currents, and 4) solve the resulting system of equations. Examples are provided to demonstrate how to apply the method to circuits with different elements like dependent sources.

1. Mesh Current Method

2. Objectives
To introduce the mesh – current method.
To formulate the mesh-current equations.
To solve electric circuits using the mesh-current
method.

3. Mesh Analysis (Loop Analysis)
MeshAnalysis is developed by applying KVL around meshes in
the circuit.
Loop (mesh) analysis results in a system of linear equations
which must be solved for unknown currents.
Reduces the number of required equations to the number of
meshes
Can be done systematically with little thinking
As usual, be careful writing mesh equations – follow sign
convention.

4. Definitions
Mesh: Loop that does not enclose other loops
Essential Branch: Path between 2 essential nodes (without
crossing other essential nodes).
How many mesh-currents?
A
# of essential nodes Ne = 4
# of essential branches Be = 6
+
No. of Mesh-currents M = Be –(Ne-1) B C
-
•Enough equations to get unknowns

5. Steps of Mesh Analysis
1. Identify the number of basic meshes.
2. Assign a current to each mesh.
3. Apply KVL around each loop to get an
equation in terms of the loop currents.
4. Solve the resulting system of linear
equations.

6. Identifying the Meshes
1kΩ 1kΩ
1kΩ
V1 + +
Mesh 1 Mesh 2 V2
– –
Assigning Mesh Currents
1kΩ 1kΩ
1kΩ
V1 + +
I1 I2 V2
– –

7. Voltages from Mesh Currents
+ VR – + VR –
R I2
R
I1
I1
V R = I1 R VR = (I1 - I2 ) R
1kΩ 1kΩ
1kΩ
V1 + +
I1 I2 V2
– –

8. Mesh-Current Equations
R1 Ω R2 Ω
R3 Ω
V1 + +
I1 I2 V2
– –
-V1 + I1 R1 + (I1 - I2) R3 = 0
I2 R2 + V2 + (I2-I1) R3 = 0

9. Mesh Current Method
6Ω
1. Assign mesh currents
2. Write mesh equations 20 Ω i1 4Ω
i1(20+6+4) + (i1-i2)(4+6) = 0 4Ω 6Ω
i2(2+4+4) + (i2-i1)(4+6) – 70 = 0
+
3. Solve mesh equations 70V
- i2 4Ω
40i1 - 10i2 = 0
2Ω 4Ω
-10i1+ 20i2 = 70
=========================
40i1 - 10i2 = 0
70i2 = 280
Solution: i1 = 1A; i2 = 4A

10. Mesh current method Cases
Case I: When a current source exists only in one mesh
Loop 1
-10 + 4i1 + 6(i1-i2) =
0
Loop 2
i2 = - 5A
No need to write a
loop equation

11. Case II: Super Mesh
When a current source exists between two meshes

12. Case III: Mesh with Dependent Sources
-75 + 5i1 + 20(i1-i2) = 0
10ix + 20(i2-i1) + 4i2 = 0 5Ω 4Ω
ix = i1 - i2 + +
75V 20Ω i3 10ix
- i1 i2 -
-75 + 5i1 + 20(i1-i2) = 0
10(i1-i2) + 20(i2-i1) + 4i2 = 0
i2 = 5A
i1 = 7A

13. Example
Use the mesh-current method to find io
Ans. Io = A

14. Solution

15. Solution