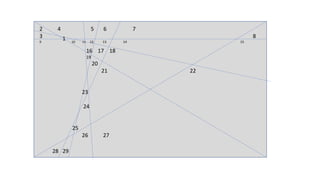
The document summarizes the maximum number of regions (Ln) that can be defined in a plane by n lines. It provides a closed-form formula of Ln=n(n+1)/2+1 and works through an example of n=7 to get Ln=29. It also shows a recursive formula approach, calculating L0 to L7 step-by-step to also arrive at Ln=29 for n=7.

1. Lines in the plane
Mohammad Junayed Khan Noor
ID: 163002029

3. PROBLEM: what’s the maximum number of regions Ln that
Can be defined in the plane by n lines?
Solution Method:
1.Closed form formula
2.Recursive formula

4. The maximum number Ln of regions in the plane that
can be defined by nstraight lines in the plane is:
Ln=n(n+1)2+1.
Suppose, n =7
Ln=7(7+1)2+1
= 29

5. Recursive Formula :
n=7
L0 =1
L1= L1-1 +1
= L0 +1
= 1+1 =2
L2= L2-1 +2
= L1+2
= 2+2
= 4
L3= L3-1 +3
= L2 +3
= 4+3 =7
L4= L4-1 +4
= L3 +4
= 7+4=11
L5= L5-1 +5
= L4+5
= 11+5=16
L6= L6-1 +6
= L5 +6
= 16+6=22
L7= L7-1 +7
= L6 +7
= 22+7=29

6. 1
2 4 5 6 7
3 8
9 10 11 12 13 14 15
16 17 18
19
20
21 22
23
24
25
26 27
28 29

7. • int main()
• { printf("Max region Solve via RF, Ln=%d",RF(n));
• CF=((n*(n+1))/2)+1;
• printf("Max region Solve via CF, Ln=%d",CF); return 0; }
• int RF(int n)
• {if(n==0)
• return 1;
• return RF(n-1)+n;}

8. Thank You