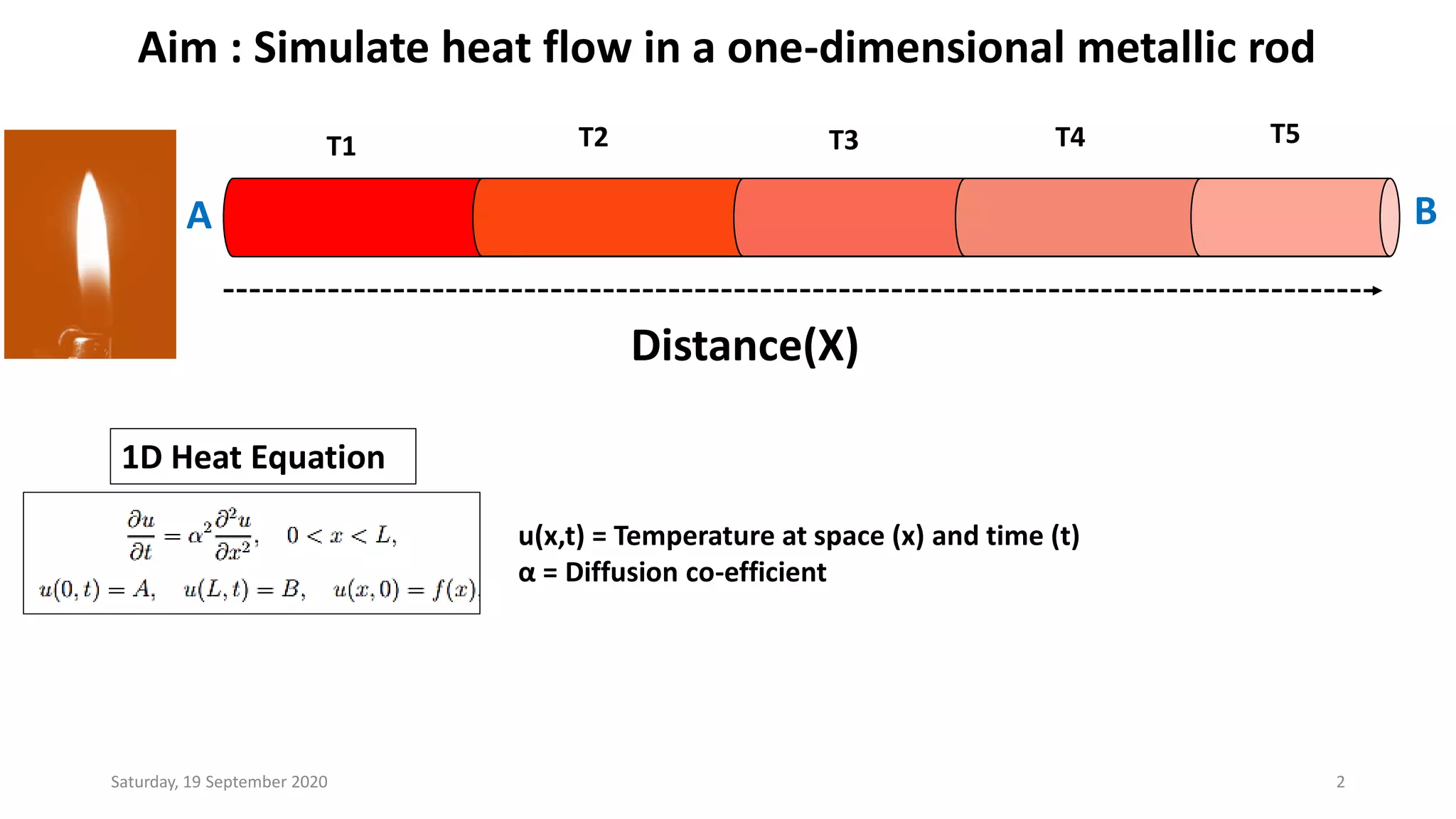
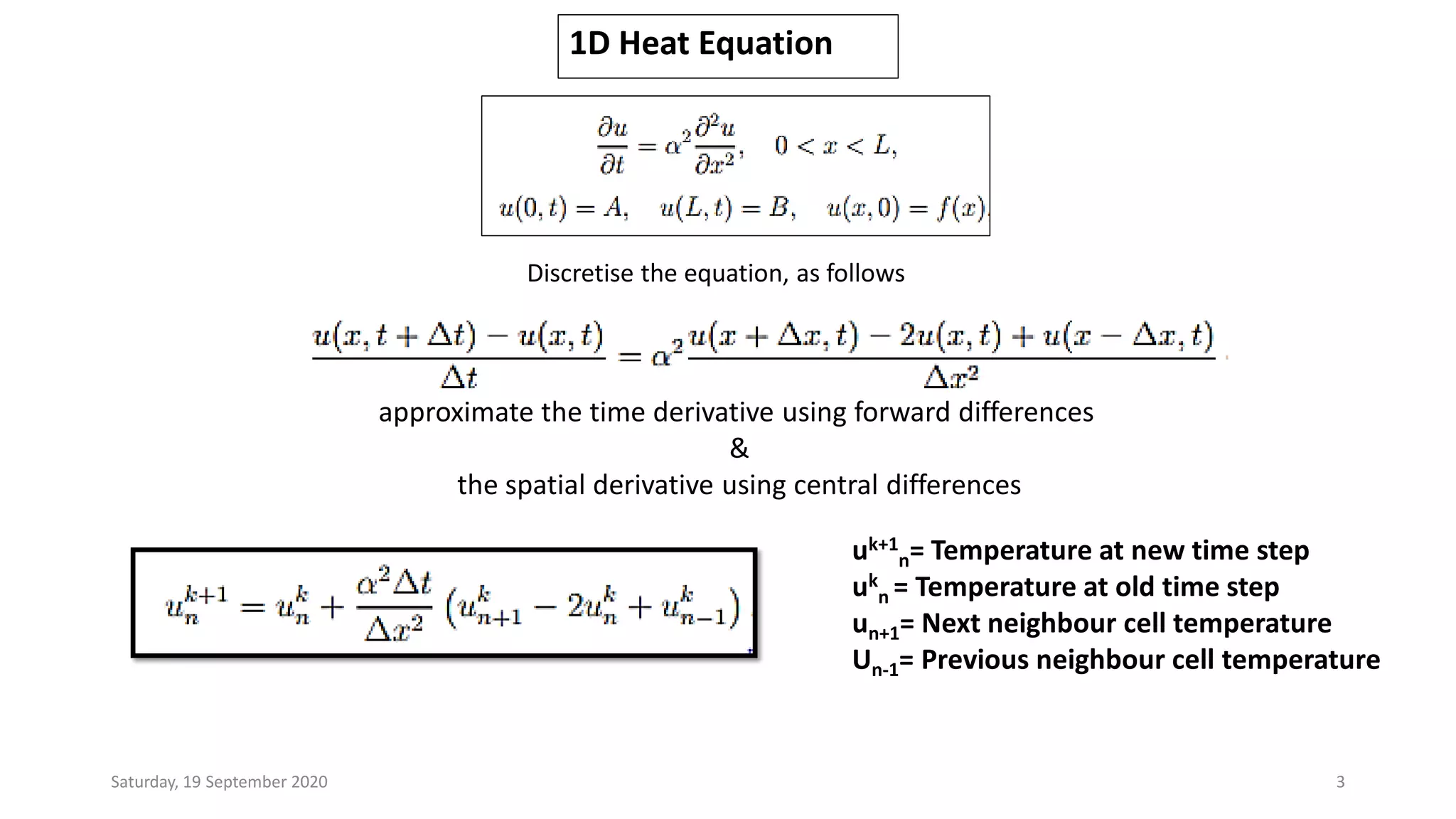
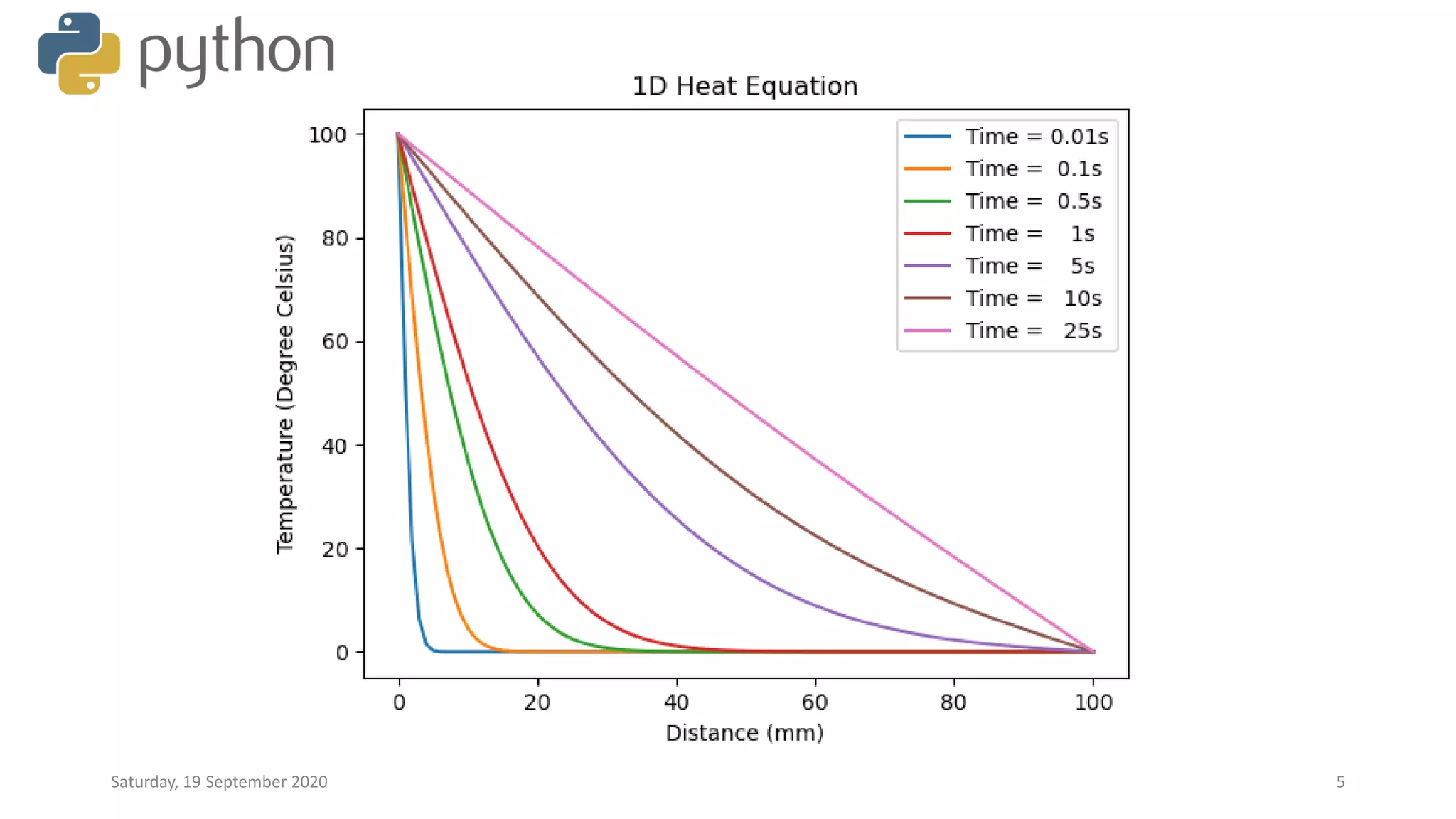
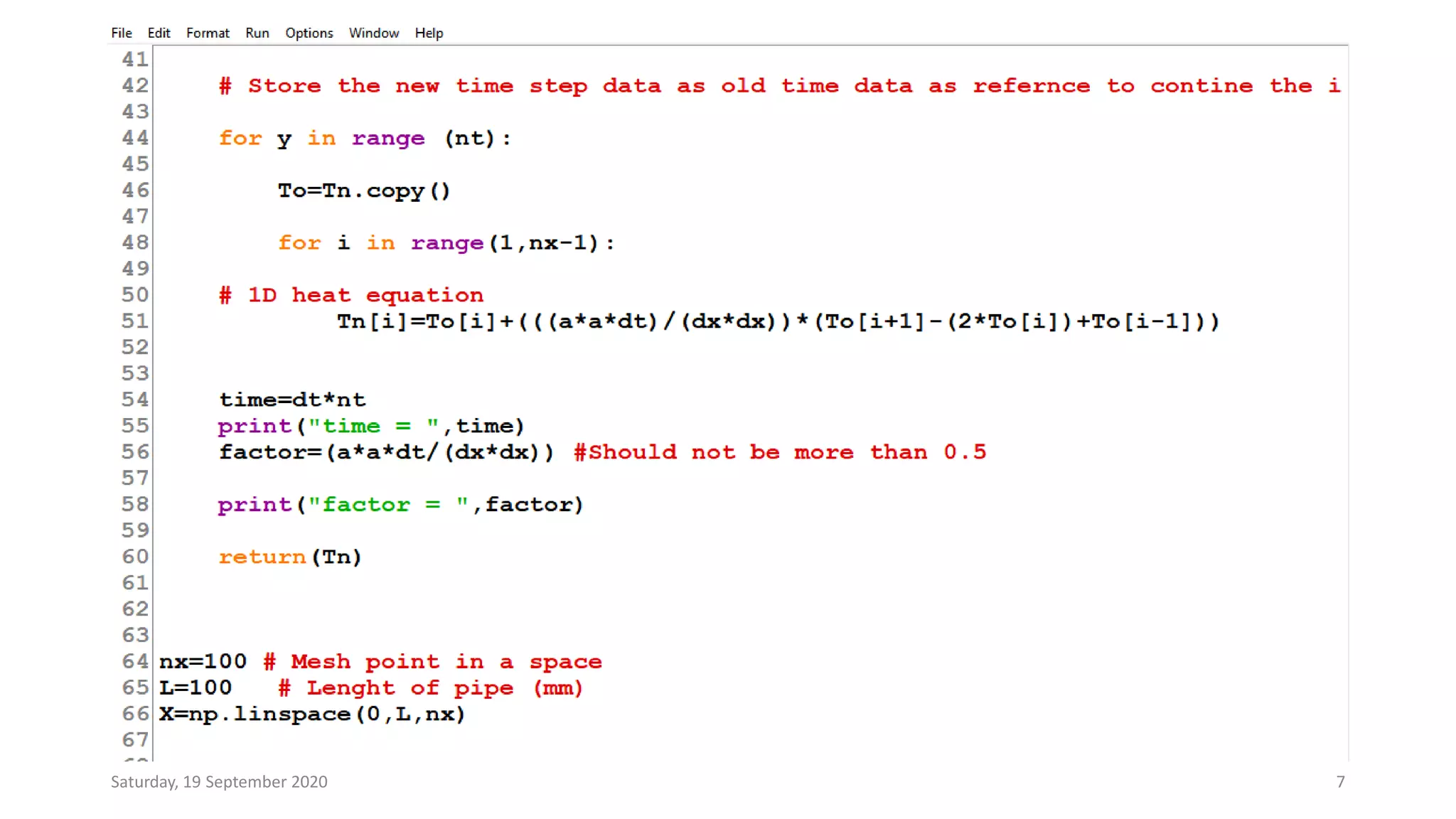
The document outlines a method for simulating heat flow in a one-dimensional metallic rod using the 1D heat equation. It discusses the discretization of the equation, employing forward differences for time derivatives and central differences for spatial derivatives. The author provides a brief introduction to the necessary variables and the finitedifference approximations involved in the simulation process.

1. Saturday, 19 September 2020 1
Manish Bhasme
CFD Engineer
MTech Chemical Plant Design (NIT Karnataka)
BTech Chemical Engineer (Nagpur University)
www.manishbhasme4@gmail.com

2. Saturday, 19 September 2020 2
Aim : Simulate heat flow in a one-dimensional metallic rod
Distance(X)
T1 T2 T4T3 T5
1D Heat Equation
A B
u(x,t) = Temperature at space (x) and time (t)
α = Diffusion co-efficient

3. Saturday, 19 September 2020 3
1D Heat Equation
Discretise the equation, as follows
approximate the time derivative using forward differences
&
the spatial derivative using central differences
uk+1
n= Temperature at new time step
uk
n = Temperature at old time step
un+1= Next neighbour cell temperature
Un-1= Previous neighbour cell temperature

4. Saturday, 19 September 2020 4
A B
xtime
x0 x1 x2 x3
uk+1
n
Uk
n+1Uk
n-1
Δx
Δt
uk
n

5. Saturday, 19 September 2020 5

6. Saturday, 19 September 2020 6

7. Saturday, 19 September 2020 7

8. Saturday, 19 September 2020 8
1D Heat Equation
u(x,t) = Temperature at space (x) and time (t)
α = Diffusion co-efficient
replace the derivatives by finite difference
approximation
uk+1
n= Temperature at new time step
uk
n = Temperature at old time step
un+1= Next neighbour cell temperature
un+1= Previous neighbour cell temperature

9. Saturday, 19 September 2020 9
Thank you
for your kind attention