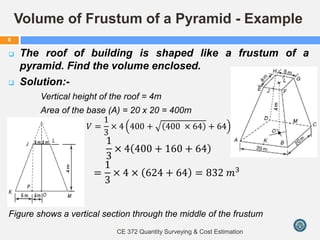
This document discusses calculating volumes of different shapes that are commonly encountered in quantity surveying and cost estimation. It begins by defining volume and identifying regular solids such as cubes, rectangular prisms, cylinders, pyramids, cones, and frustums. Formulas to calculate the volumes of these shapes are provided. The document then discusses calculating volumes of irregular shapes using trapezoidal, Simpson's, and prismoidal rules. Examples of applying these rules to practical problems are worked out. The key concepts covered are formulas for regular solids, techniques for irregular shapes, and applying these to quantity surveying problems involving excavation and construction volumes.

1. QUANTITY SURVEYING &
COST ESTIMATION
CE-372
Volumes
Quantity Surveying & Cost Estimation
SE Shahid

2. Today's Objectives
 Identify cubes, cuboids, rectangular and
triangular prisms, pyramids and cones
 Perform calculations to calculate the volumes of
the above solids
 Calculate the volume of irregular shapes using
Trapezoidal, Simpson’s and Prismoidal rule
 Solve practical problems involving volume
CE-372 Quantity Surveying & Cost Estimation
2

3. Practical Usage
 The QS has to work out quantitates from the
drawings and from site which involve volume
calculations in various items like:-
 Excavation, fill quantity, brickwork,
concreting, roof insulation, volume
calculations in road work etc
CE 372 Quantity Surveying & Cost Estimation
3

4. Volume
 Volume may be defined as the space in
a three-dimensional object. This is
different from area, which is applicable
to two-dimensional shapes
 Units of volume in metric systems are:
mm3, cm3, and m3
CE 372 Quantity Surveying & Cost Estimation
4

5. Volume of Regular Shapes
CE 372 Quantity Surveying & Cost Estimation
5
𝑉 = l x w x h
𝑉 =
𝑏𝑕
2
𝑙
𝑉 = 𝜋𝑟2
h
𝑻𝒓𝒊𝒂𝒏𝒈𝒖𝒍𝒂𝒓 𝑷𝒓𝒊𝒔𝒎
𝑹𝒆𝒄𝒕𝒂𝒏𝒈𝒖𝒍𝒂𝒓 𝑷𝒓𝒊𝒔𝒎
𝐶𝑦𝑙𝑖𝑛𝑑𝑒𝑟
l
b
r
h
l
h
w

6. CE 372 Quantity Surveying & Cost Estimation
6
𝑉 =
1
3
𝐵𝑎𝑠𝑒 𝐴𝑟𝑒𝑎 ×⊥ 𝑕
Volume of Regular Shapes
𝑷𝒚𝒓𝒂𝒎𝒊𝒅
𝑪𝒐𝒏𝒆
𝑉 =
1
3
𝜋𝑟2
𝑕
Square Base
h
l
r
.
Rectangular Base
Triangular Base
Square Base
Face
Vertex
Edge
.
.
h
h
h

7. CE 372 Quantity Surveying & Cost Estimation
7
𝑉 =
1
3
𝜋𝑕 𝑟2
+ 𝑟𝑅 + 𝑅2
Volume of Regular Shapes
𝑭𝒓𝒖𝒔𝒕𝒖𝒎 𝒐𝒇 𝒂 𝑪𝒐𝒏𝒆
𝑭𝒓𝒖𝒔𝒕𝒖𝒎 𝒐𝒇 𝒂 𝑷𝒚𝒓𝒂𝒎𝒊𝒅
𝑉 =
1
3
𝑕 𝐴 + √𝐴𝐵 + 𝐵

8. Volume of Frustum of a Pyramid - Example
 The roof of building is shaped like a frustum of a
pyramid. Find the volume enclosed.
 Solution:-
Vertical height of the roof = 4m
Area of the base (A) = 20 x 20 = 400m
𝑉 =
1
3
× 4 400 + 400 × 64 + 64
1
3
× 4 400 + 160 + 64
=
1
3
× 4 × 624 + 64 = 832 𝑚3
Figure shows a vertical section through the middle of the frustum
CE 372 Quantity Surveying & Cost Estimation
8

9. Volume of Irregular Shapes
 There are many situations where we are faced with the
determination of the volume of Irregular solids like
excavation in uneven ground for building and roads.
 Volume estimation techniques:
 Trapezoidal rule
 Simpson’s rule
 Prismoidal rule
CE 372 Quantity Surveying & Cost Estimation
9

10. Trapezoidal Rule for Volume
 Same procedure as for areas but the only difference is
that rather than the ordinates, the cross-sectional areas
are used in the volume calculations
 𝑉𝑜𝑙𝑢𝑚𝑒 =
𝑊𝑖𝑑𝑡𝑕 𝑜𝑓 𝑠𝑡𝑟𝑖𝑝 ×
1
2
𝑓𝑖𝑟𝑠𝑡 𝑎𝑟𝑒𝑎 + 𝑙𝑎𝑠𝑡 𝑎𝑟𝑒𝑎 + 𝑠𝑢𝑚 𝑜𝑓 𝑡𝑕𝑒 𝑟𝑒𝑚𝑎𝑖𝑛𝑖𝑛𝑔 𝑎𝑟𝑒𝑎𝑠
CE 372 Quantity Surveying & Cost Estimation
10
𝐴1
𝑤
𝐴2
𝐴3
𝐴4
𝐴5
𝑤
𝑤
𝑤

11. Simpson’s Rule for Volume
 The figure is divided into an even number of sections of
equal width (w), giving an odd number of areas
(Simpson’s rule will not work with an even number of
ordinates)
 𝑉𝑜𝑙𝑢𝑚𝑒 =
1
3
𝑊𝑖𝑑𝑡𝑕 𝑜𝑓 𝑠𝑡𝑟𝑖𝑝 ×
𝑓𝑖𝑟𝑠𝑡 𝑎𝑟𝑒𝑎 + 𝑙𝑎𝑠𝑡 𝑎𝑟𝑒𝑎 + 4 𝑠𝑢𝑚 𝑜𝑓 𝑒𝑣𝑒𝑛 𝑎𝑟𝑒𝑎𝑠
+2 𝑠𝑢𝑚 𝑜𝑓 𝑟𝑒𝑚𝑎𝑖𝑛𝑖𝑛𝑔 𝑜𝑑𝑑 𝑎𝑟𝑒𝑎𝑠
CE 372 Quantity Surveying & Cost Estimation
11
𝐴1
𝑤
𝐴2
𝐴3
𝐴4
𝐴5
𝑤
𝑤
𝑤

12. Prismoidal Rule for Volume
 The prismoidal rule is basically Simpson’s rule
for two strips, and may be used to determine the
volume of prisms, pyramids, cones and frustum
of cones and pyramids
 𝑉𝑜𝑙𝑢𝑚𝑒 =
ℎ
6
𝐴1 + 4 𝐴2 + 𝐴3
Where, 𝐴1= area of one end of the object
𝐴2 = area of the mid-section
𝐴3= area of the other end of the object
12

13. Volume using Trapezoidal Rule- Example
 The cross-sectional areas of a trench at 10 m
intervals are shown in Figure. Use the
trapezoidal rule and Simpson’s rule to calculate
the volume of earth excavated
CE 372 Quantity Surveying & Cost Estimation
13

14. Volume using Trapezoidal Rule - Example
A1 = 1.44m2, A2 = 1.62m2, A3 = 1.83m2, A4 = 2.0m2,
A5= 2.1m2
𝑉𝑜𝑙𝑢𝑚𝑒 = 𝑊𝑖𝑑𝑡𝑕 𝑜𝑓 𝑠𝑡𝑟𝑖𝑝
×
1
2
𝑓𝑖𝑟𝑠𝑡 𝑎𝑟𝑒𝑎 + 𝑙𝑎𝑠𝑡 𝑎𝑟𝑒𝑎 + 𝑠𝑢𝑚 𝑜𝑓 𝑡𝑕𝑒 𝑟𝑒𝑚𝑎𝑖𝑛𝑖𝑛𝑔 𝑎𝑟𝑒𝑎𝑠
𝑉𝑜𝑙𝑢𝑚𝑒 = 10 ×
1
2
1.44 + 2.1 + 1.62 + 1.83 + 2.0
= 10 × 1.77 + 1.62 + 1.83 + 2.0
= 10 × 1.77 + 5.45 = 72.2 𝑚3
CE 372 Quantity Surveying & Cost Estimation
14

15. Volume using Simpson’s Rule - Example
A1 = 1.44m2, A2 = 1.62m2,
A3= 1.83m2, A4 = 2.0m2, A5= 2.1m2
𝑉𝑜𝑙𝑢𝑚𝑒 =
1
3
𝑊𝑖𝑑𝑡𝑕 𝑜𝑓 𝑠𝑡𝑟𝑖𝑝
× 𝑓𝑖𝑟𝑠𝑡 𝑎𝑟𝑒𝑎 + 𝑙𝑎𝑠𝑡 𝑎𝑟𝑒𝑎
+ 4 𝑠𝑢𝑚 𝑜𝑓 𝑒𝑣𝑒𝑛 𝑎𝑟𝑒𝑎𝑠
+ 2 𝑠𝑢𝑚 𝑜𝑓 𝑟𝑒𝑚𝑎𝑖𝑛𝑖𝑛𝑔 𝑜𝑑𝑑 𝑎𝑟𝑒𝑎𝑠
𝑉𝑜𝑙𝑢𝑚𝑒 =
1
3
10 1.44 + 2.1 + 4 1.62 + 2.0
+ 2 1.83
=
1
3
10 3.54 + 4 3.62 + 2 1.83
=
1
3
10 3.54 + 14.48 + 3.66
=
1
3
10 21.68
= 72.267𝑚3
CE 372 Quantity Surveying & Cost Estimation
15

16. Volume using Prismoidal Rule - Example
Problem: An excavation for a basement measures 50m x 40 m at the
top and 44m x 34 m at the base. If the depth of the excavation is 3.0 m,
use the prismoidal rule to calculate the volume of the soil to be excavated.
Solution:
The dimensions at the mid-section of the excavation are:
𝐿𝑒𝑛𝑔𝑡𝑕 =
50 + 44
2
= 47 𝑚𝑊𝑖𝑑𝑡𝑕 =
40 + 34
2
= 37 𝑚
Depth of the excavation, h = 3.0 m
Area of top (A1 ) = 50 x 40 = 2000 m2
Area of mid-section (A2 ) = 47 x 37 = 1739 m2
Area of base (A3 ) = 44 x 34 = 1496 m2
𝑉𝑜𝑙𝑢𝑚𝑒 =
𝑕
6
𝐴1 + 4 𝐴2 + 𝐴3
=
3
6
2000 + 4 1739 + 1496
=
3
6
10452 = 5226 𝑚3
16
44 m
40 m
34m
50 m

17. Effort Never Dies
END
17
CE-372 Quantity Surveying & Cost Estimation