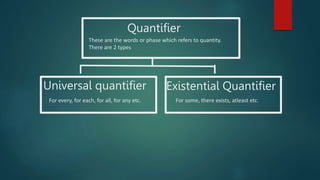
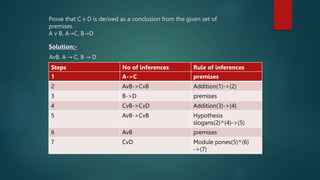
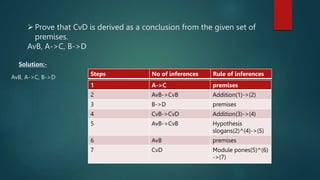
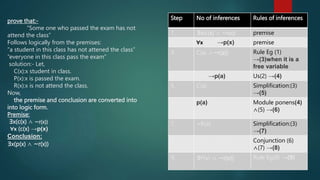
This document discusses rules of inference in predicate logic. It begins by defining rules of inference as logical forms consisting of premises and conclusions. It then defines universal and existential quantifiers. The document proceeds to list some common rules of inference for predicate logic, including universal specification, existential specification, universal generalization, and existential generalization. It provides an example of applying these rules of inference to derive a conclusion from given premises. Finally, it discusses two ways to form logical arguments using rules of inference: by translating statements into logical form and applying the rules, or by directly proving that one statement follows from others.

1. RULES OF INFERENCES.
guided By :-
Dr.Ashok Mishra
PRESENTED BY :-
Rajnikant pandey
(220101120115)

2. Rules Of Inference
 The rules of inference (also known as inference rules) are
a logical form or guide consisting of premises (or
hypotheses) and draws a conclusion.
 An argument is valid when the conclusion logically follows
from the truth values of all the premises.

3. Quantifier
These are the words or phase which refers to quantity.
There are 2 types
Universal quantifier
For every, for each, for all, for any etc.
Existential Quantifier
For some, there exists, atleast etc.

4. Rule of inferences for
predicate Logic:-
Universal specification:- Us.
Us: ∀ x P(x)->P(a).
Existential specification:- Es.
Es: ∃ x P(x)-> P(a).
Universal Generalization:- Ug.
Ug: P(a)-> ∀ x P(x).
Existential Generalization:- Eg.
Eg: P(a)-> ∃ x P(x).

5. There are two ways to form Logical
Arguments

6. Show that the following sentences imply the conclusion “It rained:”
“If it does not rain or if it is not foggy, then the sailing race will held
and the life-saving demonstration will go on.”
“If the sailing race is held, then the trophy will be awarded.”
“The trophy was not awarded.”
Let,
p = “It rains”
q = “It is foggy”
r = “The sailing race will be held”
s = “Life-saving demonstrations will go on”
t = “The trophy will be awarded”
Now, the premises and conclusion is
converted into following logical form.
(¬p ∨ ¬q) → (r ∧ s), r → t and ¬t
Conclusion: ‘p’
Step No. of Rule of inferences
1. ¬t Premise
2. r → t Premise
3. ¬r Modus tollens
(1) ∧(2) →(3)
4. ¬r ∨ ¬s Addition, (3) →(4)
5. ¬(r ∧ s) Demorgan law
(4) →(5)
6. (¬p∨¬q)→(r∧s) Premise
7. ¬(¬p∨¬q) Modus tollens
(5) ∧(6) →(7)
8. p ∧ q Demorgan law
(7) →(8)
9. p Simplification
(8) →(9)

7. Using the rule of inferences construct a valid argument using to prove
that.
“petter has two legs”
is a consequence off the premises,
“Every human being has two legs”
and “petter is a human being”
 Solution :-
Let Hx:- x is a human being.
Lx:- x has two legs.
Now premises and conclusion are translated to the following logical form
Step No of inferences Rule of inferences
2 H(p) premises
3 H(p)->L(p) Rule Us (1)->(3)
4 L(P) Modune pones (2)^(3)-
>(4)
1 ∀ x (H(x)->L(x)) Premises

8. Prove that C v D is derived as a conclusion from the given set of
premises.
A v B, A→C, B→D
Solution:-
AvB, A → C, B → D
Steps No of inferences Rule of inferences
1 A->C premises
2 AvB->CvB Addition(1)->(2)
3 B->D premises
4 CvB->CvD Addition(3)->(4)
5 AvB->CvB Hypothesis
slogans(2)^(4)->(5)
6 AvB premises
7 CvD Module pones(5)^(6)
->(7)

9. Using the rules of inferences construct a valid argument to prove that
“Some fierce creatures do not drink coffee.”
is a consequence (conclusion) of the premises
“All lions are fierce.”
“Some lions do not drink coffee.”
Let,
L(x): “x is a lion.”
F(x): “x is fierce.” and
C(x): “x drinks coffee.”
Now, the premises and conclusion are
translated into the following logical form.
Premises: ∀x(L(x)→ F(x))
∃x (L(x) ∧ ¬C(x))
Conclusion:
∃x (F(x) ∧ ¬C(x))
Step No. of inferences Rule of inferences
1. ∃x (L(x) ∧ ¬C(x)) Premise
2. L(x) ∧ ¬C(x) E.s. (1) →(2)
3. L(x) Simplification
(2) →(3)
4. ¬C(x) Simplification
(2) →(4)
5. ∀x (L(x)→ F(x)) Premise
6. L(x) → F(x) U.s. (5) →(6)
7. F(x) Modus ponens
(3) ∧(6) →(7)
8. F(x) ∧ ¬C(x) Conjunction
(4) ∧(7) →(8)
9 ∃x (F(x) ∧ ¬C(x)) E.g. (8) →(9)

10. Prove that CvD is derived as a conclusion from the given set of
premises.
AvB, A->C, B->D
Solution:-
AvB, A->C, B->D
Steps No of inferences Rule of inferences
1 A->C premises
2 AvB->CvB Addition(1)->(2)
3 B->D premises
4 CvB->CvD Addition(3)->(4)
5 AvB->CvB Hypothesis
slogans(2)^(4)->(5)
6 AvB premises
7 CvD Module pones(5)^(6)
->(7)

11. prove that:-
“Some one who passed the exam has not
attend the class”
Follows logically from the premises:
“a student in this class has not attened the class”
“everyone in this class pass the exam”
solution:- Let,
C(x):x student in class.
P(x):x is passed the exam.
R(x):x is not attend the class.
Now,
the premise and conclusion are converted into
into logic form.
Premise:
∃x(c(x) ∧ ~r(x))
∀x (c(x) →p(x)
Conclusion:
∃x(p(x) ∧ ~r(x))
Step No of inferences Rules of inferences
1. ∃x(c(x) ∧ ~r(x)) premise
2. ∀x (c(x) →p(x) premise
3. C(a) ∧~r(a)) Rule Eg (1)
→(3)when it is a
free variable
4. C(a) →p(a) Us(2) →(4)
5. C(a) Simplification:(3)
→(5)
6. p(a) Module ponens(4)
∧(5) →(6)
7. ~R(a) Simplification:(3)
→(7)
8. P(a) ∧ ~r(a)) Conjunction (6)
∧(7) →(8)
9. ∃P(x) ∧ ~r(x)) Rule Eg(8) →(9)

12. THANK YOU!!!!