Документ представляет собой лекцию о дереве ванэмдебоаса (van emdeboas tree) — структуре данных для динамического хранения множества целочисленных ключей с эффективными операциями поиска и манипуляции, выполняемыми за время O(log log u). Описаны основные операции, включая insert, delete и lookup, а также структура и алгоритмы, связанные с этой эффективной структурой данных. Лекция относится к курсу 'Алгоритмы и структуры данных' в Сибирском государственном университете телекоммуникаций и информатики.

1. Лекция 9Дерево ванЭмдеБоаса(van EmdeBoas tree)
КурносовМихаил Георгиевич
E-mail: mkurnosov@gmail.com
WWW: www.mkurnosov.net
Курс “Алгоритмы и структуры данных”
Сибирский государственный университет телекоммуникаций и информатики (Новосибирск)
Осенний семестр, 2014

2. Дерево ванЭмдеБоаса(Van EmdeBoas tree)
2
Дерево ванЭмдеБоаса(van EmdeBoas tree, vEBtree)– это структура данных, реализующая операции Lookup, Insert, Delete, Min, Max, Successor, Predecessor над динамическими множествами(sets)за времяO(lg(lg(n)))
Операции ExtractMinи DecreaseKeyмогут быть реализованы на базе операций Min, Delete и Insert

3. Дерево ванЭмдеБоаса(Van EmdeBoas tree)
Дерево ванЭмдеБоаса(van EmdeBoas tree, vEBtree)– это дерево поиска (search tree)для хранения целочисленных m-битных ключей
Ключ –целое неотрицательное число из множества 푈=0,1,…,푢−1,푢=2푚
Основные операции (Insert, Delete, Lookup, Min, Max) выполняются за время 푂(loglog푢), что асимптотически лучше, чем 푂log푛в сбалансированных бинарных деревьях поиска (AVL tree, red-black tree)
Автор: Peter van EmdeBoas, 1975
Peter van EmdeBoas. Preserving order in a forest in less than logarithmic time// Proceedings of the 16th Annual Symposium on Foundations of Computer Science, 1975, p. 75-84

4. Дерево ванЭмдеБоаса(Van EmdeBoas tree)
4
Дерево ванЭмдеБоаса(van EmdeBoas tree, vEBtree)– это дерево поиска (search tree)для хранения целочисленных неотрицательных ключей из множества {0, 1, …, u–1}
Например, пусть ключи –это целые числа из множества {0, 1, …, 1000}
Тогда u= 1000 +1 = 1001(мощность множества ключей)
Для хранения ключа с максимальным значением 1000 необходимо log21000+1=9.97+1=10бит
Максимальноезначение ключа
Количество бит для хранения ключа
255
8 (uint8_t)
65535
16 (uint16_t)
4294967295
32 (uint32_t)
264–1
64 (uint64_t)

5. Прямаяадресация
5
Динамическое множество значений из универсума푈=0,1,…,푢−1можно хранить в массиве 퐴[0,..푢−1]из 푢бит
Элемент 퐴[푥]хранит 1, если значение 푥принадлежит множеству, 0 –в противном случае
Операции Insert,Delete, Member/Lookup выполняются за время O(1)
Min, Max, Successor, Predecessor выполняются за времяO(u) – требуется просмотреть весь битовый вектор A
1
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
1
18
3
2
Универсум из 3-х элементов 푼=ퟎ,ퟑ,ퟏퟖ,풖=ퟐퟎ
Successor(0) = 3, Successor(18) = NULL
Predecessor(18) = 3
Min
Max

6. Наложение бинарного дерева
6
Динамическое множество значений из универсума푈=0,1,…,푢−1можно хранить в массиве 퐴[0,..푢−1]из 푢бит
Элементы битового вектора –это листья бинарного дерева, внутренний узел содержит 1 тогда и только тогда, когда некоторый лист в его поддереве содержит 1 (внутренний узел содержит логическое ИЛИ дочерних узлов)
푼=ퟐ,ퟑ,ퟒ,ퟓ,ퟕ,ퟏퟒ,ퟏퟓ,풖=ퟏퟔ
Min–от корня вниз, выбирая самый левый узел с 1
Max–от корня вправо, выбирая самый правый узел с 1
Predecessor(x) –от листа к корню, пока не войдем справа в узел с левым дочерним элементом 1, затем вниз, выбирай крайний справа узел с 1
Высота дерева h= O(log(u)) Сложность операцийMin/Max/Predecessor –O(log(u))
Сложность Lookup –O(1)

7. Наложение деревапостоянной высоты
7
푼=ퟐ,ퟑ,ퟒ,ퟓ,ퟕ,ퟏퟒ,ퟏퟓ,풖=ퟏퟔ
Динамическое множество значений из универсума 푈=0,1,…,푢−1можно хранить в массиве 퐴[0,..푢−1]из 푢бит
Элементы битового вектора –это листья бинарного дерева, внутренний узел содержит 1 тогда и только тогда, когда некоторый лист в его поддереве содержит 1 (внутренний узел содержит логическое ИЛИ дочерних узлов)
Можно ли наложить на бинарный вектор дерево постоянной высоты (не зависящей отu)?
h=O(log(u))

8. Наложение деревапостоянной высоты
푼=ퟐ,ퟑ,ퟒ,ퟓ,ퟕ,ퟏퟒ,ퟏퟓ,풖=ퟏퟔ
Пусть размер универсума푢=22푚, так что 푢=2푚целое число
Наложим на битовый вектор дерево степени 푢=2푚
Узлы на уровне 1 –это результат ИЛИ для группы из 푢=4бит
Узлы на уровне 1 –это элементы массива summary[0..푢−1]
summary[i] –это логическое ИЛИ подмассива퐴푖푢..푖+1푢−1
summary[i] –это кластер(cluster)i
Бит xмассива Aнаходится в кластерес номером 푥/푢
Дерево степени 16=4
summary[0]
summary[3]

9. Наложение деревапостоянной высоты
푼=ퟐ,ퟑ,ퟒ,ퟓ,ퟕ,ퟏퟒ,ퟏퟓ,풖=ퟏퟔ
Insert:A[x] = 1, summary[푥/푢] = 1 O(1)
Min/Max: ищем крайний слева(справа)элемент summary[i] = 1,затем в кластере iнаходим крайней слева (справа) бит 1O(풖)
Successor/Predecessor: ищем в пределах кластера вправо (влево) бит 1, если не нашли, то ищем кластер справа (слева) от 푥/푢, который содержит 1 и в нем отыскиваем крайний слева (справа) бит 1O(풖)
Delete: A[x] = 0, summary[푥/푢] = логическое ИЛИ битов кластера iO(풖)
summary[0]
summary[3]

10. Рекурсивная структура
푼=ퟐ,ퟑ,ퟒ,ퟓ,ퟕ,ퟏퟒ,ퟏퟓ,풖=ퟏퟔ
Имеем универсум из 푢элементов
Создаем структуры хранящие 푢=푢 12элементов, которые хранят структуры по푢 14элементов, которые хранят структуры по 푢 18элементов, … до структур по 2 элемента
Считаем, что 푢=22푘 , для некоторого целого k
Тогда u, u1/2, u1/4и т.д. –целые числа
uиз множества {2, 4, 16, 256, 65536, …}
summary[0]
summary[3]

11. Рекурсивная структура
푼=ퟐ,ퟑ,ퟒ,ퟓ,ퟕ,ퟏퟒ,ퟏퟓ,풖=ퟏퟔ
Значение xрасполагается в кластере с номером 푥/푢
Будем считать, что x –это log2u –битовое число, тогда номер кластера определяется log2(u)/ 2старшими битами числа x
high푥=푥/푢
В своем кластереxнаходится в позиции 푥mod푢, которая задается младшими log2(u)/ 2битами x
low푥=푥mod푢
indexℎ,푙=ℎ푢+푙
summary[0]
summary[3]

12. ПротоструктураванЭмдеБоаса(proto-vEB)
12
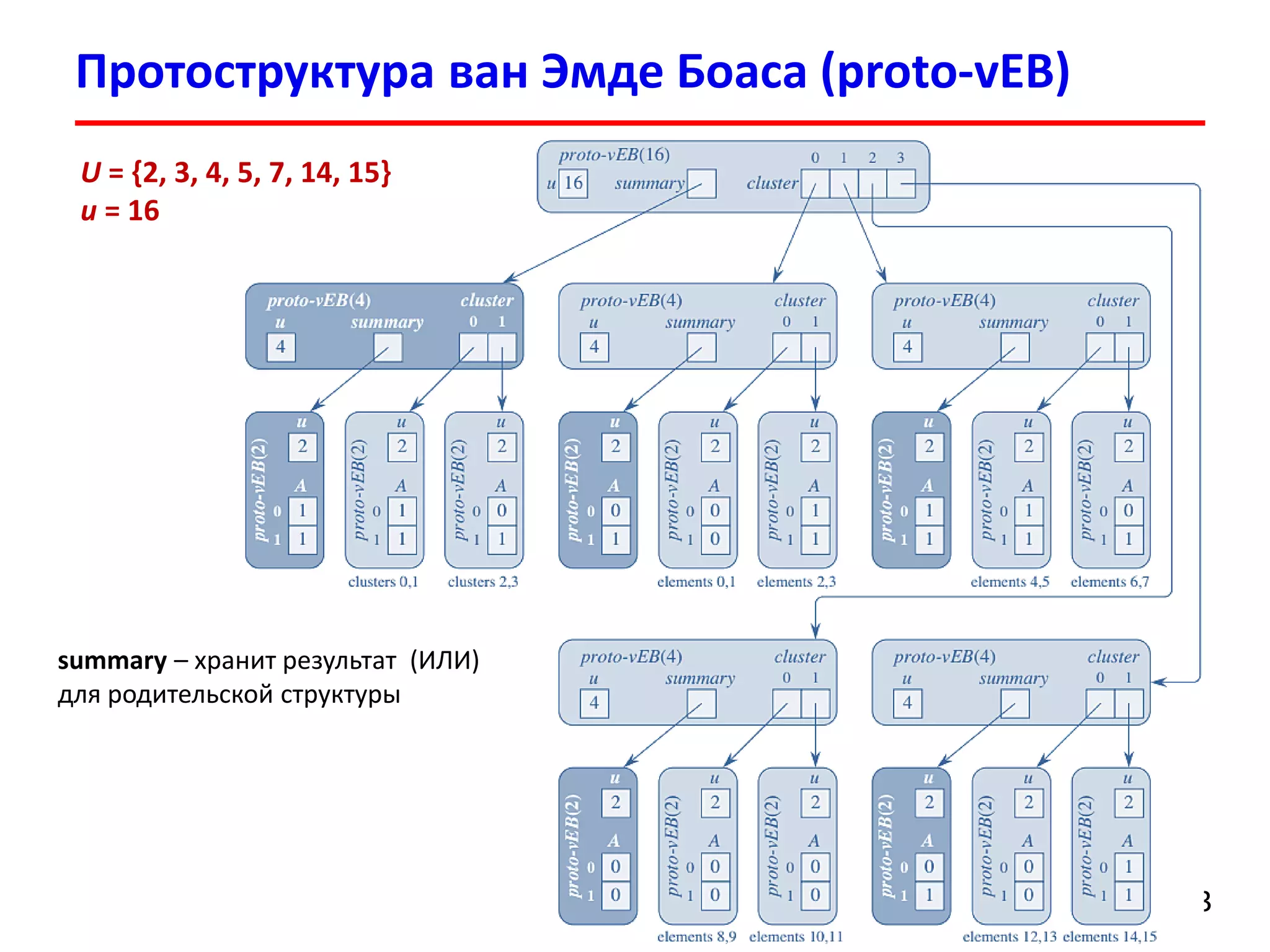
Обозначим через proto-vEB(u)протоструктуруванЭмдеБоаса, содержащее ключи из множества {0, 1, …, u–1}
Каждый узел дерева proto-vEB(u) содержит:
значение u –размер универсума
если u= 2
это базовый размер и структура содержит массив A[0..1] из двух бит
иначе
указатель summaryна структуру proto-vEB(푢)
массив cluster[0..푢−1] указателей на структурыproto-vEB(푢)

13. ПротоструктураванЭмдеБоаса(proto-vEB)
13
U= {2, 3, 4, 5, 7, 14, 15}
u= 16
summary–хранит результат (ИЛИ) для родительской структуры

14. Поиск элемента
14
U= {2, 3, 4, 5, 7, 14, 15}
u= 16
functionLookup(V, x)
ifV.u= 2 then
returnV.A[x]
node = V.cluster[high(x)]
returnLookup(node, low(x))
end function

15. Поиск элемента
15
U= {2, 3, 4, 5, 7, 14, 15}
u= 16
functionLookup(V, x)
ifV.u= 2 then
returnV.A[x]
node = V.cluster[high(x)]
returnLookup(node, low(x))
end function
Lookup(V, 14)
high(14) = 3
low(14) = 2
Lookup(V, 2)
high(2) = 1
low() = 0
Lookup(V, 0)
return A[0]
1410= 11102
210= 102

16. Поиск элемента
16
U= {2, 3, 4, 5, 7, 14, 15}
u= 16
functionLookup(V, x)
ifV.u= 2 then
returnV.A[x]
node = V.cluster[high(x)]
returnLookup(node, low(x))
end function
Lookup(V, 14)
high(14) = 3
low(14) = 2
1410= 11102
210= 102
T(u) = T(풖) + O(1) = O(log(logu))
Lookup(V, 2)
high(2) = 1
low() = 0
Lookup(V, 0)
return A[0]

17. Структурадерева ванЭмдеБоаса
17
Обозначим через vEB(u)дерево ванЭмдеБоаса, содержащее ключи из множества {0, 1, …, u–1}
Каждый узел дерева vEB(u) содержит:
указатель summaryна дерево푣퐸퐵2log2푢 2
массив cluster[0..2log2푢 2−1] указателей на корни деревьев 푣퐸퐵2log2푛 2
минимальный minэлемент в дереве vEB(копии min нет в поддеревьях cluster[…])
максимальный maxэлемент в дереве vEB
значение u

18. Пример дерева vEB(16)
18
vEB(16)
u: 16
min: 2
max: 15
summary
cluster[]:
vEB(4)
u: 4
min: 0
max: 3
summary
cluster[]:
vEB(4)
u: 4
min: 3
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: 0
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(4)
u: 4
min: 2
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: 1
max: 1
vEB(4)
u: 4
min: -
max: -
summary
cluster[]:
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(4)
u: 4
min: 0
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: 0
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: 1
max: 1
Дерево vEB(16), содержащее ключи 2, 3, 4, 5, 7, 14, 15
Данные только в полях min, max

19. Пример дерева vEB(16)
19
vEB(16)
u: 16
min: 2
max: 15
summary
cluster[]:
vEB(4)
u: 4
min: 0
max: 3
summary
cluster[]:
vEB(4)
u: 4
min: 3
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: 0
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(4)
u: 4
min: 2
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: 1
max: 1
vEB(4)
u: 4
min: -
max: -
summary
cluster[]:
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(4)
u: 4
min: 0
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: 0
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: 1
max: 1
15
2
7
5
11
01
00
10
1
0
3
4
14
Дерево vEB(16), содержащее ключи 2, 3, 4, 5, 7, 14, 15
Данные только в полях min, max

20. Структурадерева ванЭмдеБоаса
20
Значения(value) ассоциированные с ключами хранятся только в полях min, maxузлов(min.value, max.value)
Ключ не хранится в узлах (аналогия с trie, prefix tree)– биты ключа распределены по узламна пути от корня к листьям
Время выполнения операций не зависит от количества nэлементов в дереве
Хранение min и max в узлах позволяет сократить глубину спуска по дереву при поиске минимального/максимального элемента, а также при поиске следующего элемента (successor) и предыдущего(predecessor)

21. Структурадерева ванЭмдеБоаса
21
В ключе “закодирован”путь в дереве vEB
Пример, ключи из множества {0, 1, …, 65535}, u= 65536 = 216
Дерево vEB(65536)
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
Key:
Индекс в cluster[] уровня 0 (корень)
Индекс в cluster[] уровня 1
Индекс уровня 2
high(key) = 101100112 = 17910
high(x) = 210
high(x) = 310

22. Структурадерева ванЭмдеБоаса
22
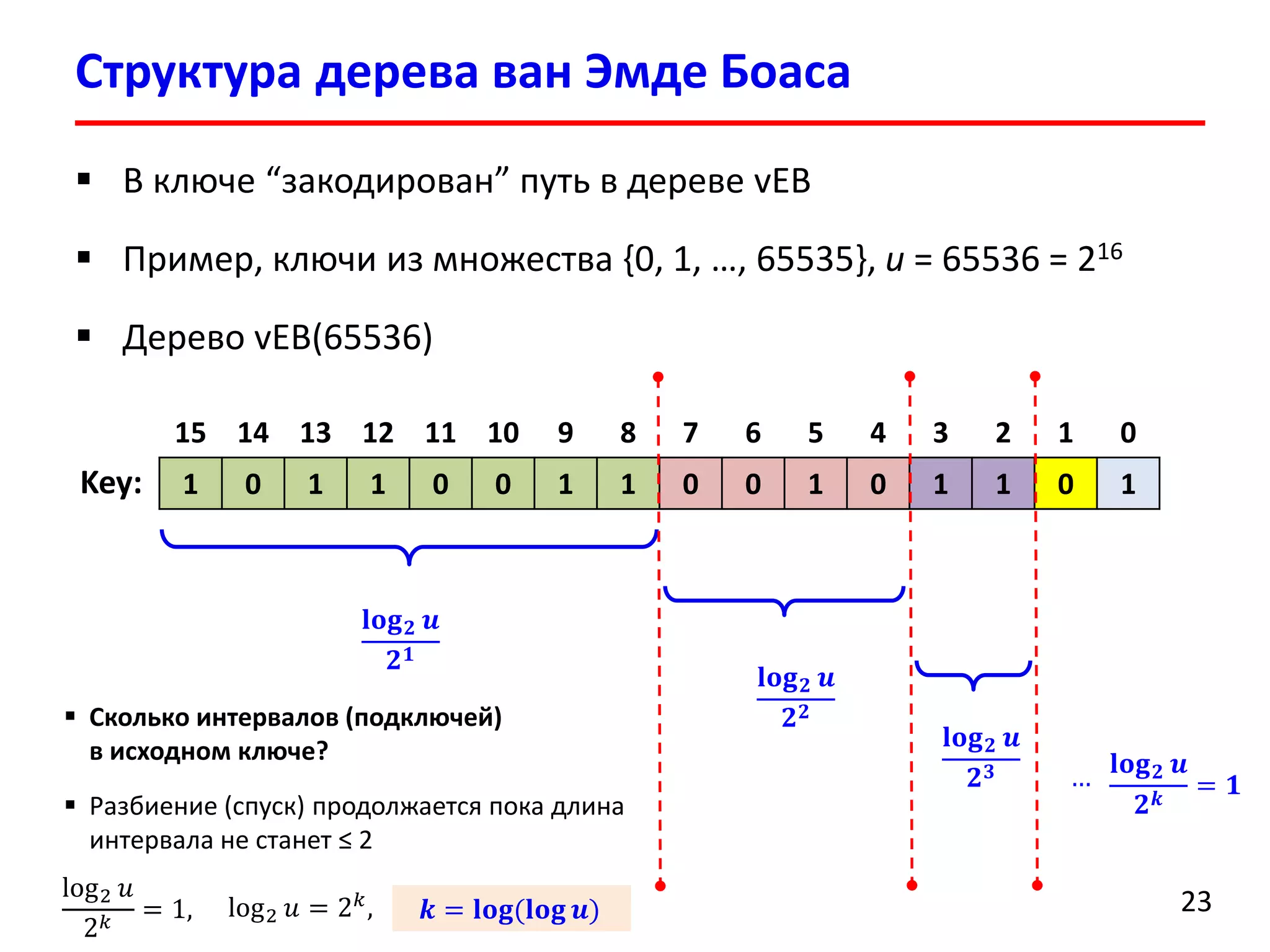
В ключе “закодирован”путь в дереве vEB
Пример, ключи из множества {0, 1, …, 65535}, u= 65536 = 216
Дерево vEB(65536)
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
Key:
Индекс в cluster[] уровня 0 (корень)
Индекс в cluster[] уровня 1
Индекс уровня 2
high(key) = 101100112 = 17910
high(x) = 210
high(x) = 310 퐥퐨퐠ퟐ풖 ퟐퟏ 퐥퐨퐠ퟐ풖 ퟐퟐ 퐥퐨퐠ퟐ풖 ퟐퟑ
…
Размер интервала (подключа) уменьшается по геометрической прогрессии

23. log2푢 2푘=1,
log2푢=2푘,
Структурадерева ванЭмдеБоаса
23
В ключе “закодирован”путь в дереве vEB
Пример, ключи из множества {0, 1, …, 65535}, u= 65536 = 216
Дерево vEB(65536)
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
Key: 퐥퐨퐠ퟐ풖 ퟐퟏ 퐥퐨퐠ퟐ풖 ퟐퟐ 퐥퐨퐠ퟐ풖 ퟐퟑ
…
Сколько интервалов (подключей) в исходном ключе?
Разбиение (спуск) продолжается пока длина интервала не станет ≤ 2 퐥퐨퐠ퟐ풖 ퟐ풌=ퟏ
풌=퐥퐨퐠(퐥퐨퐠풖)

24. Структурадерева ванЭмдеБоаса
24
Дерево vEB(65536), u= 65536 = 216
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
Key:
Индекс в cluster[] уровня 0 (корень)
Индекс в cluster[] уровня 1
Индекс уровня 2
high(key) = 101100112 = 17910
high(x) = 210
high(x) = 310
풉풊품풉풙= 풙 ퟐ logퟐ풖 ퟐ
풍풐풘풙=풙modퟐ logퟐ풖 ퟐ
Половина старших битов
Половина младших битов
ℎ푖푔ℎ45869= 4586928=179
푙표푤45869=45869mod256=45

25. Поиск экстремальных(min/max)элементов
25
functionvEB_Min(tree)
returntree.min
end function
functionvEB_Max(tree)
returntree.max
end function
Вместе с деревом хранятся минимальныйи максимальный элементы, доступ к ним осуществляется за время O(1)
TMin= O(1)
TMax= O(1)

26. Поиск элемента в дереве vEB
26
functionvEB_Lookup(tree, key)
ifkey = tree.min.keythen
returntree.min
ifkey = tree.max.keythen
returntree.max
// Дерево vEB(2) данных кроме min, max не имеет
iftree.u= 2
returnNULL
hi = high(key) // Номер поддеревав cluster[]
lo = low(key)// Новый ключ
returnvEB_Lookup(tree.cluster[hi], lo)
end function
TLookup= O(log(logu))
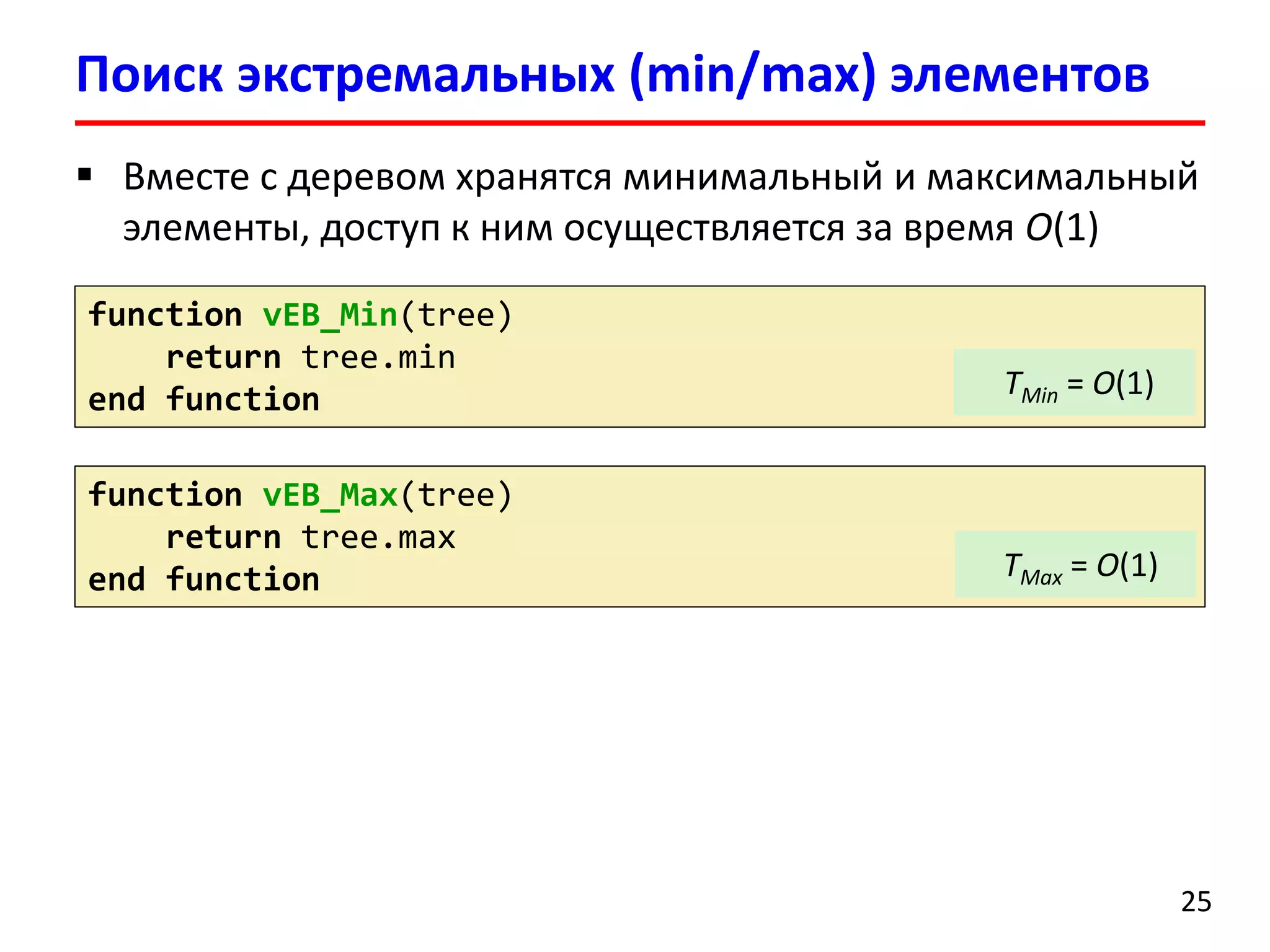
Рекурсивно спускаемся по дереву проверяя поля min и max
С каждым рекурсивным вызовом длина ключа keyуменьшается:
key -> low(key) -> low(low(key)) -> low(low(low(key))) -> …

27. Поиск в дереве vEB(16)элемента 7 (01112)
27
vEB(16)
u: 16
min: 2
max: 15
summary
cluster[]:
vEB(4)
u: 4
min: 0
max: 3
summary
cluster[]:
vEB(4)
u: 4
min: 3
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: 0
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(4)
u: 4
min: 2
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: 1
max: 1
vEB(4)
u: 4
min: -
max: -
summary
cluster[]:
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(4)
u: 4
min: 0
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: 0
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: 1
max: 1
Дерево vEB(16), содержащее ключи 2, 3, 4, 5, 7, 14, 15
high(7) = high(0111) = 1
low(7) = low(0111) = 3
Запись для key= 7
в поле
max
Lookup(vEB(16), 7)
Lookup(vEB(4), 3)
1
2

28. Добавление элемента в пустое дерево vEB
28
functionvEB_AddEmpty(tree, key, value)
// Дерево пусто–заполняем поля min, max
tree.min.key= key
tree.min.value= value
tree.max.key= key
tree.max.value= value
end function
TAddEmpty= O(1)
При вставке элемента в пустое дерево, заносим его в поля min и max
После вставки в дереве один элемент и min = max

29. Добавление элемента в дерево vEB
29
functionvEB_Add(tree, key, value)
iftree.min= NULL then
// Дерево пусто
vEB_AddEmpty(tree, key, value)
end if
if key < tree.min.keythen
// Заменим minновым значением, а старый min
// добавим в поддерево
swap(<min.key, min.value>, <key, value>)
end if
Добавление элемента в дерево выполняется рекурсивно, при каждом вызове (для каждого поддерева) обрабатываем возможные ситуации:
Если поддерево пусто, добавляем элемент в поля min и max
Если ключ меньше ключа min, заменяем в minключ на новый, астарый ключ min вставим в поддерево позднее (см. ниже)

30. Добавление элемента в дерево vEB
30
iftree.u> 2 then
hi = high(key)
lo = low(key)
ifvEB_Min(tree.cluster[hi]) = NULL then
// Поддерево hi пусто
vEB_Add(tree.summary, hi)
vEB_AddEmpty(tree.cluster[hi], lo)
else
vEB_Add(tree.cluster[hi], lo)
end if
ifkey > tree.max.keythen
// Обновляем max
tree.max.key= key
tree.max.value= value
end if
end function
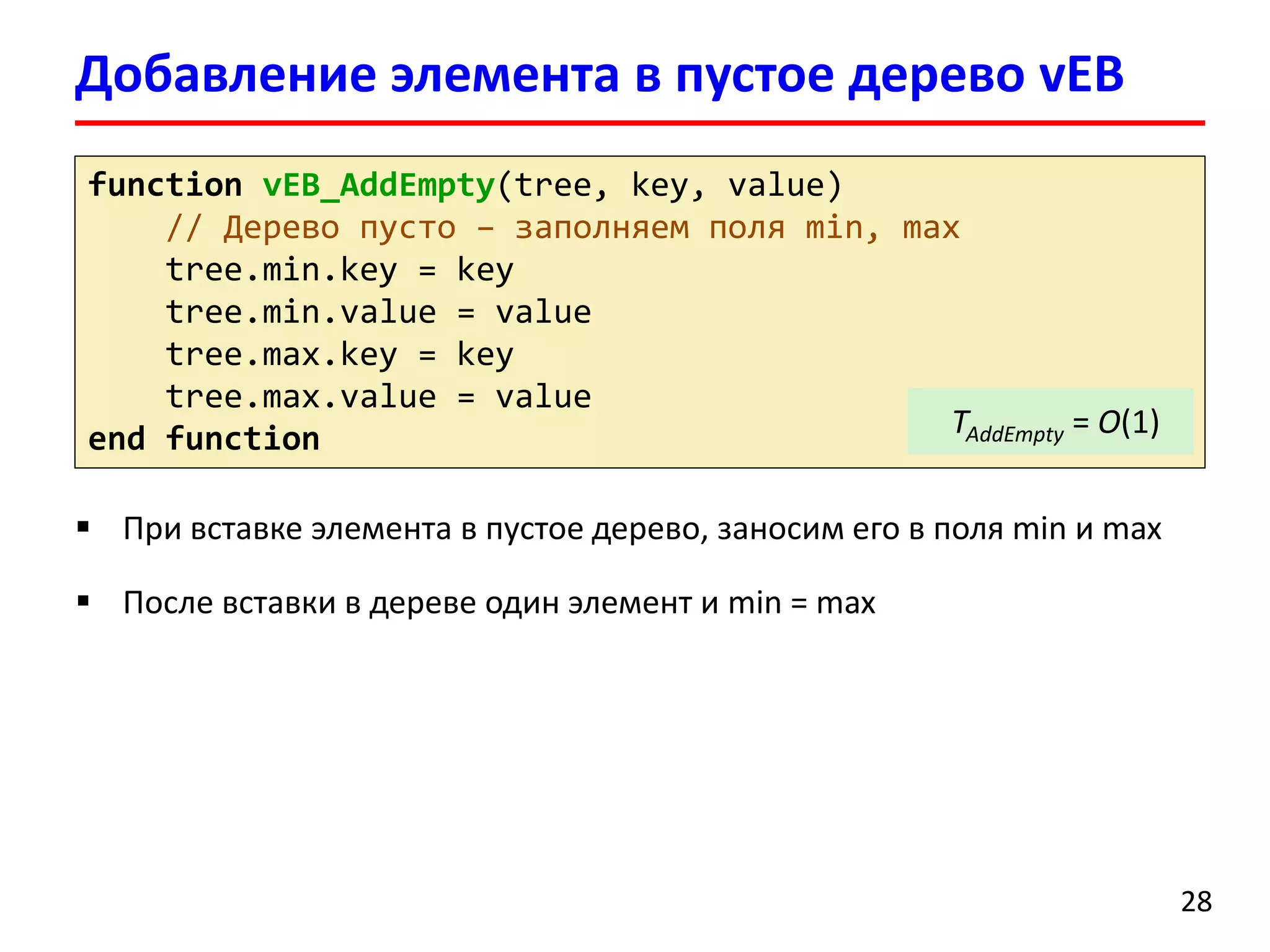
Рекурсивно спускаемся пока, не дойдем до узла с u≤ 2
TAdd= O(log(log(u)))

31. Вставка в дерево vEB(16)элемента 6 (01102)
31
vEB(16)
u: 16
min: 2
max: 15
summary
cluster[]:
vEB(4)
u: 4
min: 0
max: 3
summary
cluster[]:
vEB(4)
u: 4
min: 3
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: 0
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(4)
u: 4
min: 2
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: 1
max: 1
vEB(4)
u: 4
min: -
max: -
summary
cluster[]:
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(2)
u: 2
min: -
max: -
vEB(4)
u: 4
min: 0
max: 3
summary
cluster[]:
vEB(2)
u: 2
min: 0
max: 1
vEB(2)
u: 2
min: 1
max: 1
vEB(2)
u: 2
min: 0
max: 1
high(6) = high(0110) = 1
low(6) = low(0110) = 2
vEB_Add(vEB(16), 6)
hi = 1, lo = 2
vEB_Min(vEB(16).cluster[1]) != NULL
vEB_Add(vEB(16).cluster[1], 2)
hi = 1, lo = 0
vEB_Min(vEB(4).cluster[1]) != NULL
vEB_Add(vEB(4).cluster[1], 0)
Обмениваем min=1и key=0
7
6
Add(vEB(16), 6)
1
Add(vEB(4), 2)
2
Add(vEB(2), 0)
3

32. Удаление элемента из дерева vEB
32
Рекурсивно спускаемся по дереву vEBи ищем узел, которому соответствует ключ
Если дерево(узел) содержит один элемент (min = max), удаляем min и max
Если в дереве (узле) 2 элемента (u= 2), удаляем один из них и корректируем min и max;в дереве остается один элементи min = max
…
HOME WORK
Изучить алгоритм удаления элемента из дерева vEB
[CLRS_3ed, C.590]“Удаление элемента”

33. Эффективность дерева vEB
33
Высота дерева определяется значением u–длинной ключа
При первомвызове Lookup длина ключа log2푢
На второмрекурсивном вызове длина ключа log2푢 2(в два раза короче –low(key))
На третьемвызове длина ключа: log2푢 22(в четыре раза короче –low(low(key)))
и т.д. пока не дойдем до узла с u= 2log2푢 21, log2푢 22, log2푢 23,⋯, log2푢 2푘=1
log2푢=2푘,
푘=log2log2푢
Дерево vEB(u) имеет высоту푶(퐥퐨퐠ퟐ퐥퐨퐠ퟐ풖)

34. Дерево ванЭмдеБоаса(van EmdeBoas tree)
34
Операция
Худший случай (worst case)
Add(key,value)
푂(log2log2푢)
Lookup(key)
푂(log2log2푢)
Delete(key)
푂(log2log2푢)
Min
푂(1)
Max
푂(1)
Сложность по памяти: O(2logu)= O(u)
u–максимальное значение ключа + 1

35. Плюсы и минусы дерева vEB
35
Достоинства дерева vEB
Вычислительная сложность операций 푂(log2log2푢):
асимптотически быстрее чем сбалансированные деревья поиска (AVL tree, red-back tree)
сложность операций не зависит от количества nэлементов в дереве (в словаре)
Недостатки
Применимо лишь в случае целых неотрицательных ключей
Высокие требования к памяти O(u) = O(2logu)

36. Применение дерева vEB
36
Словарь(ассоциативный массив) с целочисленными ключами
Сортировкаnцелочисленных ключейза время 푂푛∙log2log2푢–быстрее чем поразрядная сортировка(Radix sort)
Реализация кучии применение в алгоритме Дейкстрыпостроения кратчайшего пути в графе: реализация DecreaseKeyза время 푂log2log2푢, таким образом итоговое время работы алгоритма Дейкстрысоставит 푂퐸∙log2log2푢

37. Задания
37
Изучить алгоритм удаления элемента из дерева vEB[CLRS_3ed, C.590]“Удаление элемента”
Разобраться с функциями удаления, поиска следующего(Successor)и предыдущего(Predecessor)элементов в vEB