Документ посвящен теории авл-деревьев (AVL trees) как сбалансированных двоичных деревьев поиска, описывая основные операции их работы и алгоритмы балансировки. Рассматриваются алгоритмы добавления и удаления узлов, а также вычислительная сложность операций. Также приводится анализ эффективности авл-деревьев и их свойств связи с последовательностью Фибоначчи.

1. Лекция 3АВЛ-деревья(AVL trees)
КурносовМихаил Георгиевич
E-mail: mkurnosov@gmail.com
WWW: www.mkurnosov.net
Курс “Алгоритмы и структуры данных”
Сибирский государственный университет телекоммуникаций и информатики (Новосибирск)
Осенний семестр, 2014

2. Двоичные деревья поиска
2
Двоичное дерево поиска(Binary search tree, BST) – этодвоичное дерево, в котором:
1)каждый узел (node) имеет не более двух дочерних узлов (child nodes)
2)каждый узел содержитключ(key) и значение(value)
3)ключи всех узлов левого поддерева меньшезначения ключародительского узла
4)ключи всех узлов правого поддерева больше значения ключа родительского узла
15
Барсук
180
Тигр
200
Лев
Value:
Key:
Двоичные деревья поиска используются для реализации словарей(map, associative array)и множеств (set)

3. Двоичные деревья поиска
3
60
Волк
35
Рысь
90
Ягуар
8
Лиса
15
Барсук
180
Тигр
200
Лев
4000
Слон
600
Медведь
9 узлов, высота (height)= 3, глубина (depth) = 3
Value:
Key:
Min
Max

4. Двоичные деревья поиска
4
1
Value1
2
Value2
1.Операции над BST имеют трудоемкость пропорциональную высоте hдерева
2.В среднем случае высота дерева O(logn)
3.В худшем случае элементы добавляютсяпо возрастанию (убыванию) ключей – дерево вырождается в список длины O(n)
bstree_add(1, value1)
bstree_add(2, value2)
bstree_add(3, value3)
bstree_add(4, value4)
3
Value3
4
Value4
NULL
NULL
NULL

5. Сбалансированное дерево поиска (Self-balancing binary search tree)–дерево поиска, в котором высота поддеревьев любого узла различается не более чем на заданную константу k
Cбалансированныедеревьяпоиска:
Красно-черныедеревья(Red-blacktrees)
АВЛ-деревья(AVLtrees)
2-3-деревья(2-3trees)
B-деревья(B-trees)
AAtrees
…
Сбалансированные деревья поиска
5

6. AVL-деревья
АВЛ-дерево (AVL tree) –сбалансированное по высоте двоичное дерево поиска, в котором у любой вершины высота левого и правого поддеревьев различаются не более чем на 1
x
h
h -2
h -1
Авторы: Адельсон-Вельский Г.М., Ландис Е.М. Один алгоритм организации информации // Доклады АН СССР. –1962. Т.146, №2. – C. 263–266.
Right
Left
Адельсон-Вельский Г.М.
Ландис Е.М.
GNU libavl
libdict
Python avllib
avlmap

7. AVL tree
7
Операция
Среднийслучай (Average case)
Худший случай (Worst case)
Add(key,value)
O(logn)
O(logn)
Lookup(key)
O(logn)
O(logn)
Remove(key)
O(logn)
O(logn)
Min
O(logn)
O(logn)
Max
O(logn)
O(logn)
Сложность по памяти(space complexity): O(n)

8. AVL-деревья
8
Основная идея
Если вставка или удаление элемента приводит к нарушению сбалансированности дерева, то необходимо выполнить его балансировку
Коэффициент сбалансированности узла (balance factor)– это разность высот его левого и правого поддеревьев
В АВЛ-дереве коэффициент сбалансированности любого узла принимает значения из множества {-1, 0, 1}
Высота узла (height) –это длина наибольшего пути от него до дочернего узла, являющего листом

9. Высота узла (Node height)
9
10
Height 3
5
20
12
4
7
2
10
2
1
0
0
1
0
1
Высота пустого поддерева (NULL) равна -1

10. Коэффициент сбалансированности
10
10
1
5
0
20
1
12
0
4
1
7
-1
2
0
10
0
Key:
Balance:
Balance(Node)=
Height(Left)–Height(Right)
Высота поддерева = 1
Balance(4)=
= 0 -(-1) = 1

11. Коэффициент сбалансированности
11
10
2
5
0
20
0
4
1
7
-1
2
0
10
0
Key:
Balance:
Balance(Node)=
Height(Left)–Height(Right)
Высота поддерева = 1
Balance(4)=
= 0 -(-1) = 1
Не AVL-дерево

12. Балансировка дерева (Rebalancing)
12
После добавления нового элемента необходимо обновить коэффициенты сбалансированности родительских узлов
Если любой родительский узел принял значение -2 или 2, то необходимо выполнить балансировку поддерева путем поворота (rotation)
Повороты:
Одиночный правый поворот (R-rotation, single right rotation)
Одиночный левый поворот (L-rotation, single left rotation)
Двойной лево-правый поворот (LR-rotation, double left-right rotation)
Двойной право-левый поворот (RL-rotation, double right-left rotation)

13. Правый поворот (R-rotation)
13
2
3
1
2
0
1
В левое поддерево узла 3 добавили элемент 1
Дерево с корнем в узле 3не сбалансированноH(Left) =1 >H(Right) =-1
Необходимо увеличить высоту правого поддерева
Left LeftСase

14. Правый поворот (R-rotation)
14
2
3
1
2
0
1
Left LeftСase
Поворачиваем ребро, связывающее корень и его левыйдочерний узел, вправо

15. Правый поворот (R-rotation)
15
2
3
1
2
0
1
Left LeftСase
Поворачиваем ребро, связывающее корень и его левыйдочерний узел, вправо
0
2
0
1
0
3
Деревосбалансированно

16. Правый поворот (R-rotation)
16
P
L
T1
T2
T3
X
Правый поворот в общем случае
L
P
T2
T3
X
T1
В левое поддерево вставлен элемент Х
Дерево не сбалансированноH(Left) > H(Right)

17. Правый поворот (R-rotation)
17
P
L
T1
T2
T3
X
L
P
T2
T3
X
T1
P.left= L.right
L.right= P
P.height= 1 + max(P.left.height,
P.right.height)
L.height= 1 + max(L.left.height,
P.height)

18. Левый поворот (L-rotation)
18
В правое поддерево узла 1 вставлен элемент 3
Поворачиваем ребро, связывающее кореньи его правый дочерний узел, влево
-2
1
-1
2
0
3
0
2
0
1
0
3
Деревосбалансированно
Right RightСase

19. Левый поворот (L-rotation)
19
-2
P
-1
R
0
x
0
2
0
1
0
3
Деревосбалансированно
P.right= R.left
R.left= P
P.height= 1 + max(P.left.height,
P.right.height) + 1
R.height= 1 + max(R.right.height,
P.height) + 1
Right RightСase

20. Двойной лево-правый поворот (LR-rotation)
20
LR-поворот выполняется после добавления элемента в правое поддерево левого дочернего узла дерева
L
T1
R
T2
T3
X
X
или
P
T4
1. L-поворот левого поддерева P
2. R-поворот нового дерева свершиной P
Left Right Case

21. Двойной лево-правый поворот (LR-rotation)
21
LR-поворот выполняется после добавления элемента в правое поддерево левого дочернего узла дерева
L
T1
R
T2
T3
X
X
или
P
T4
1. L-поворот левого поддерева P
P.left= L_rotate(P.left)

22. Двойной лево-правый поворот (LR-rotation)
22
LR-поворот выполняется после добавления элемента в правое поддерево левого дочернего узла дерева
R
T3
L
T1
T2
X
X
P
T4
1. L-поворот левого поддерева P

23. Двойной лево-правый поворот (LR-rotation)
23
LR-поворот выполняется после добавления элемента в правое поддерево левого дочернего узла дерева
R
T3
L
T1
T2
X
X
P
T4
2. R-поворот нового дереваc корнем P
P = R_rotate(P)

24. Двойной лево-правый поворот (LR-rotation)
24
LR-поворот выполняется после добавления элемента в правое поддерево левого дочернего узла дерева
R
T3
X
T1
T2
X
P
L
T4
2. R-поворот нового дереваc корнем P

25. Двойной лево-правый поворот (LR-rotation)
25
LR-поворот выполняется после добавления элемента в правое поддерево левого дочернего узла дерева
2
3
-1
1
0
2
2
3
1
2
0
1
L-поворот
0
2
0
3
0
1
R-поворот

26. Двойной право-левый поворот (RL-rotation)
26
RL-поворот выполняется после добавления элемента в левое поддерево правого дочернего узла дерева
-2
1
1
3
0
2
L-поворот
-1
2
0
3
-2
1
R-поворот
0
2
0
3
0
1
Right Left case
P.right= R_rotate(P.right)
P = L_rotate(P)

27. Повороты в АВЛ-дереве
27
Вычислительная сложность любого поворота O(1)
Любой поворот сохраняет свойства бинарного дерева поиска (распределение ключей по левыми и правым поддеревьям)

28. Анализ эффективности АВЛ-деревьев
28
Оценим сверху высоту hАВЛ-дерева, содержащего Nвнутренних узлов(узлов, имеющих дочерние вершины)
Обозначим через N(h) минимальное количество внутреннихузлов необходимых для формирования АВЛ-дерева высоты h
h= 0
h= 1
h= 2
h= 3
АВЛ-деревья различной высоты
N(0) = 0
N(1) = 1
N(2) = 2
N(3) = 4

29. Анализ эффективности АВЛ-деревьев
29
Значения N(h): 0, 1, 2, 4, 7, 12, 20, 33, 54, …
Видно, что
N(h) = N(h–1) + N(h–2) + 1, для h= 2, 3, …
Значения последовательности N(h)можно выразить через значения последовательности Фибоначчи
푭풏=푭풏−ퟏ+푭풏−ퟐ, 퐹0=0, 퐹1=1
Значения 푭풏: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
Значения N(h): 0, 1, 2, 4, 7, 12, 20, 33, 54, …
N(h) = F(h+2) –1, для h≥0

30. Анализ эффективности АВЛ-деревьев
30
Выразим из N(h)= F(h+ 2) –1значение высоты hАВЛ-дерева, состоящего из N(h) внутренних узлов
По формуле Бинеможно найти приближенное значение n-гочлена последовательности Фибоначчи
–золотое сечение(gold ratio)

31. Анализ эффективности АВЛ-деревьев
31
푵풉= 흋풉+ퟐ ퟓ −ퟏ> 흋풉+ퟐ ퟓ −ퟐ 5푁ℎ+2>휑ℎ+2
log휑(5푁ℎ+2)>ℎ+2
ℎ<log휑5(푁ℎ+2)−2
ℎ<log휑5+log휑(푁ℎ+2)−2
ℎ< lg5lg휑 + 1log2휑 log2(푁ℎ+2)−2
ℎ< lg5lg휑 + lg2lg휑 log2(푁ℎ+2)−2

32. Анализ эффективности АВЛ-деревьев
32
ℎ< lg5lg휑 + lg2lg휑 log2(푁ℎ+2)−2
ℎ<1.6723+1.44log2(푁ℎ+2)−2
풉<ퟏ.ퟒퟒퟎퟓ퐥퐨퐠ퟐ푵풉+ퟐ−ퟎ.ퟑퟐퟕퟕ
풉=푶(퐥퐨퐠풏+ퟐ)

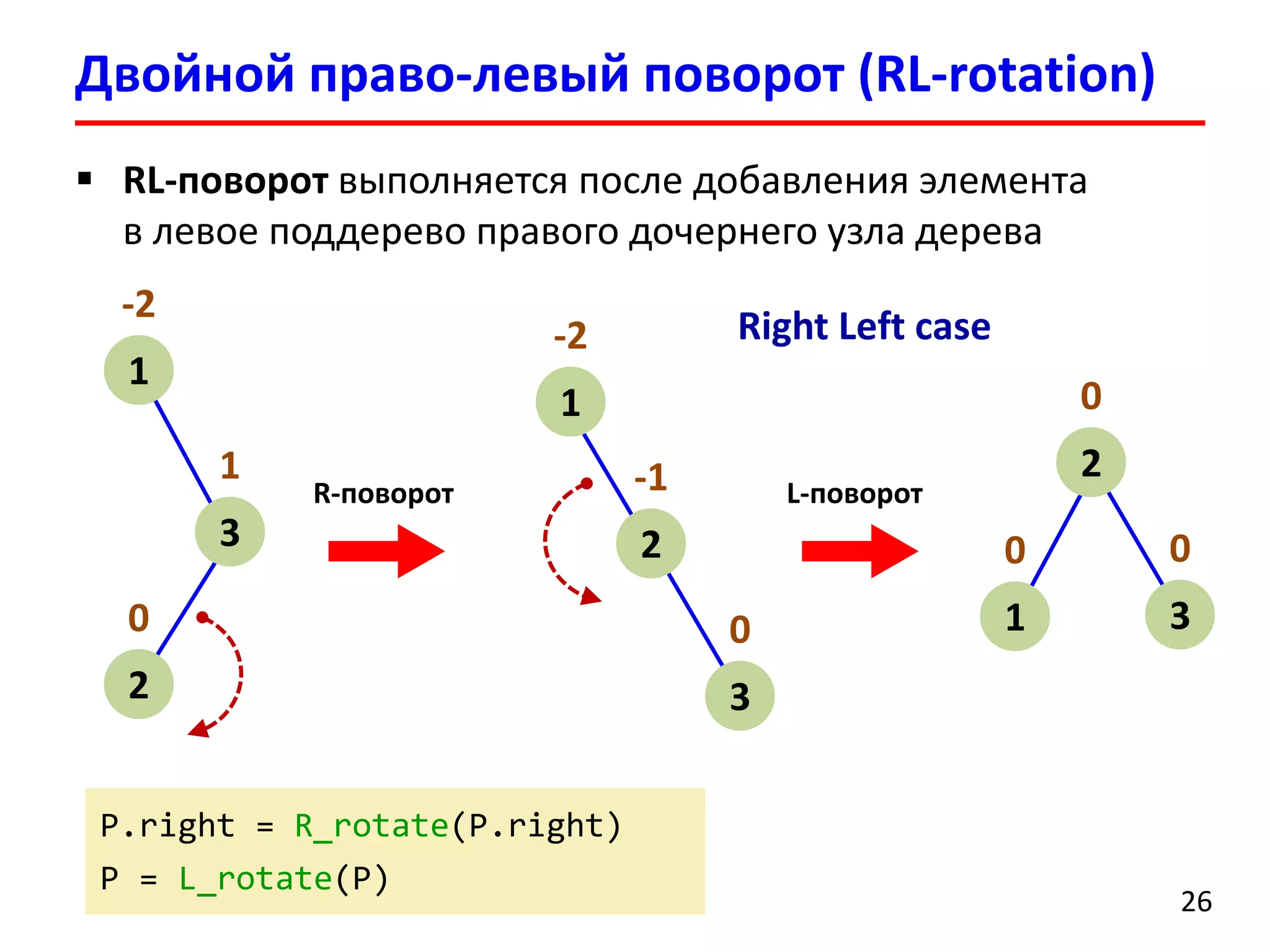
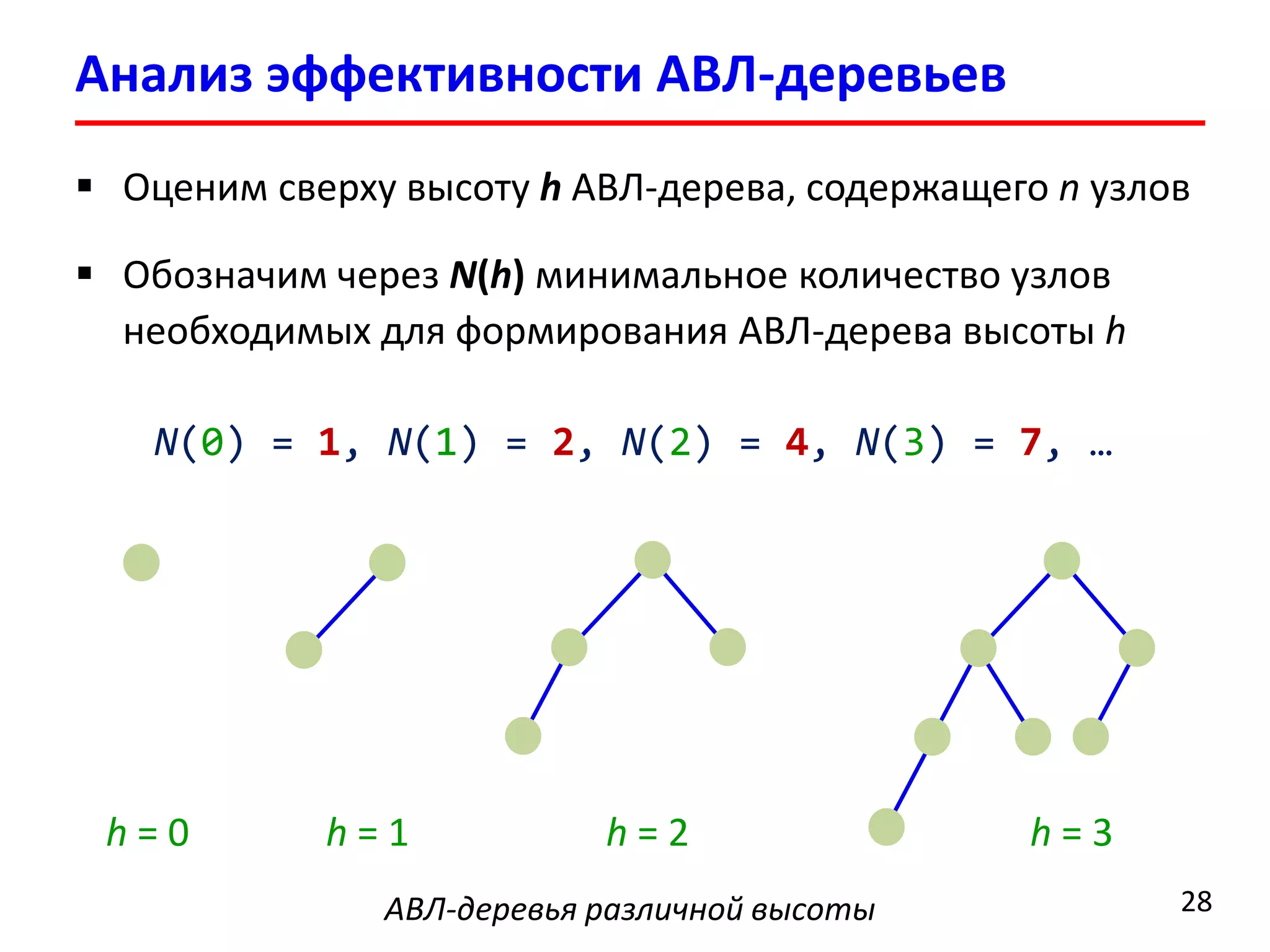
33. Анализ эффективности АВЛ-деревьев
33
Оценка сверху высоты h(n) АВЛ-дерева[Knuth, Vol.3], [Wirth89]:
log2(n+ 1) ≤ h(n) <1.4405∙log2(n+ 2) –0.3277
Оценка сверху высоты h(n) АВЛ-дерева[Levitin2006]: 퐥퐨퐠ퟐ풏≤풉풏<ퟏ.ퟒퟒퟎퟓ퐥퐨퐠ퟐ풏+ퟐ−ퟏ.ퟑퟐퟕퟕ

34. AVL Tree
34
structavltree{
intkey;
char*value;
intheight;
structavltree*left;
structavltree*right;
};

35. intmain()
{
structavltree*tree = NULL;
tree = avltree_add(tree, 10, "10");
tree = avltree_add(tree, 5, "5");
tree = avltree_add(tree, 3, "3");
tree = avltree_add(tree, 11, "11");
tree = avltree_add(tree, 12, "12");
avltree_print(tree);
avltree_free(tree);
return0;
}
Построение AVL-дерева
35
11
5
3
10
12

36. intmain()
{
structavltree*tree = NULL;
tree = avltree_add(tree, 5, "5");
tree = avltree_add(tree, 3, "3");
/* Code */
tree = avltree_delete(tree, 5);
avltree_free(tree);
return0;
}
Удаление узлов из AVL-дерева
36

37. voidavltree_free(structavltree*tree)
{
if(tree == NULL)
return;
avltree_free(tree->left);
avltree_free(tree->right);
free(tree);
}
Удаление всех узлов из AVL-дерева
37
TFree= O(n)
11
5
3
10
12

38. structavltree*avltree_lookup(
structavltree*tree, intkey)
{
while(tree != NULL) {
if(key == tree->key) {
returntree;
} elseif(key < tree->key) {
tree = tree->left;
} else{
tree = tree->right;
}
}
returntree;
}
Поиск узла по ключу
38
TLookup= O(log2n)

39. structavltree*avltree_create(intkey,
char*value)
{
structavltree*node;
node = malloc(sizeof(*node));
if(node != NULL) {
node->key = key;
node->value = value;
node->left = NULL;
node->right = NULL;
node->height = 0;
}
returnnode;
}
Создание узла
39
TCreate= O(1)

40. intavltree_height(structavltree*tree)
{
return(tree != NULL) ? tree->height : -1;
}
intavltree_balance(structavltree*tree)
{
returnavltree_height(tree->left) –
avltree_height(tree->right);
}
Высота и баланс узла (поддерева)
40
THeight= O(1)
TBalance= O(1)

41. structavltree*avltree_add(
structavltree*tree, intkey, char*value)
{
if(tree == NULL) {
/* Insert new item */
returnavltree_create(key, value);
}
Добавление узла
41

42. if(key < tree->key) {
/* Insert into left subtree*/
tree->left = avltree_add(tree->left,
key, value);
if(avltree_height(tree->left) –
avltree_height(tree->right) == 2)
{
/* Subtreeis unbalanced */
if(key < tree->left->key) {
/* Left leftcase */
tree = avltree_right_rotate(tree);
} else{
/* Left right case */
tree = avltree_leftright_rotate(tree);
}
}
}
Добавление узла (продолжение)
42

43. else if (key > tree->key) {
/* Insert into right subtree*/
tree->right = avltree_add(tree->right,
key, value);
if(avltree_height(tree->right) -
avltree_height(tree->left) == 2)
{
/* Subtreeis unbalanced */
if(key > tree->right->key) {
/* Right rightcase */
tree = avltree_left_rotate(tree);
} else{
/* Right left case */
tree = avltree_rightleft_rotate(tree);
}
}
}
Добавление узла (продолжение)
43

44. tree->height =
imax2(avltree_height(tree->left),
avltree_height(tree->right)) + 1;
returntree;
}
Добавление узла (окончание)
44
TAdd= O(log2n)
Поиск листа для вставки нового элемента выполняется за время O(log2n)
Повороты выполняются за время O(1), их количество не может превышать O(log2n)при подъеме от нового элемента к корню (высота AVL-дерева O(log2n))

45. structavltree*avltree_right_rotate(
structavltree*tree)
{
structavltree*left;
left = tree->left;
tree->left = left->right;
left->right = tree;
tree->height = imax2(
avltree_height(tree->left),
avltree_height(tree->right)) + 1;
left->height = imax2(
avltree_height(left->left),
tree->height) + 1;
returnleft;
}
R-поворот (left leftcase)
45
T
L
X

46. structavltree*avltree_left_rotate(
structavltree*tree)
{
structavltree*right;
right = tree->right;
tree->right = right->left;
right->left = tree;
tree->height = imax2(
avltree_height(tree->left),
avltree_height(tree->right)) + 1;
right->height = imax2(
avltree_height(right->right),
tree->height) + 1;
returnright;
}
L-поворот (right right case)
46
T
R
X

47. structavltree*avltree_leftright_rotate(
structavltree*tree)
{
tree->left = avltree_left_rotate(tree->left);
returnavltree_right_rotate(tree);
}
LR-поворот (left right case)
47

48. structavltree*avltree_rightleft_rotate(
structavltree*tree)
{
tree->right = avltree_right_rotate(tree->right);
returnavltree_left_rotate(tree);
}
RL-поворот (right left case)
48

49. voidavltree_print_dfs(structavltree*tree, intlevel)
{
inti;
if(tree == NULL)
return;
for(i = 0; i < level; i++)
printf(" ");
printf("%dn", tree->key);
avltree_print_dfs(tree->left, level + 1);
avltree_print_dfs(tree->right, level + 1);
}
Вывод дерева на экран
49

50. tree = avltree_add(tree, 10, "10");
tree = avltree_add(tree, 5, "5");
tree = avltree_add(tree, 3, "3");
tree = avltree_add(tree, 11, "11");
tree = avltree_add(tree, 12, "12");
avltree_print_dfs(tree, 0);
Вывод дерева на экран
50
5
3
11
10
12
11
5
3
10
12

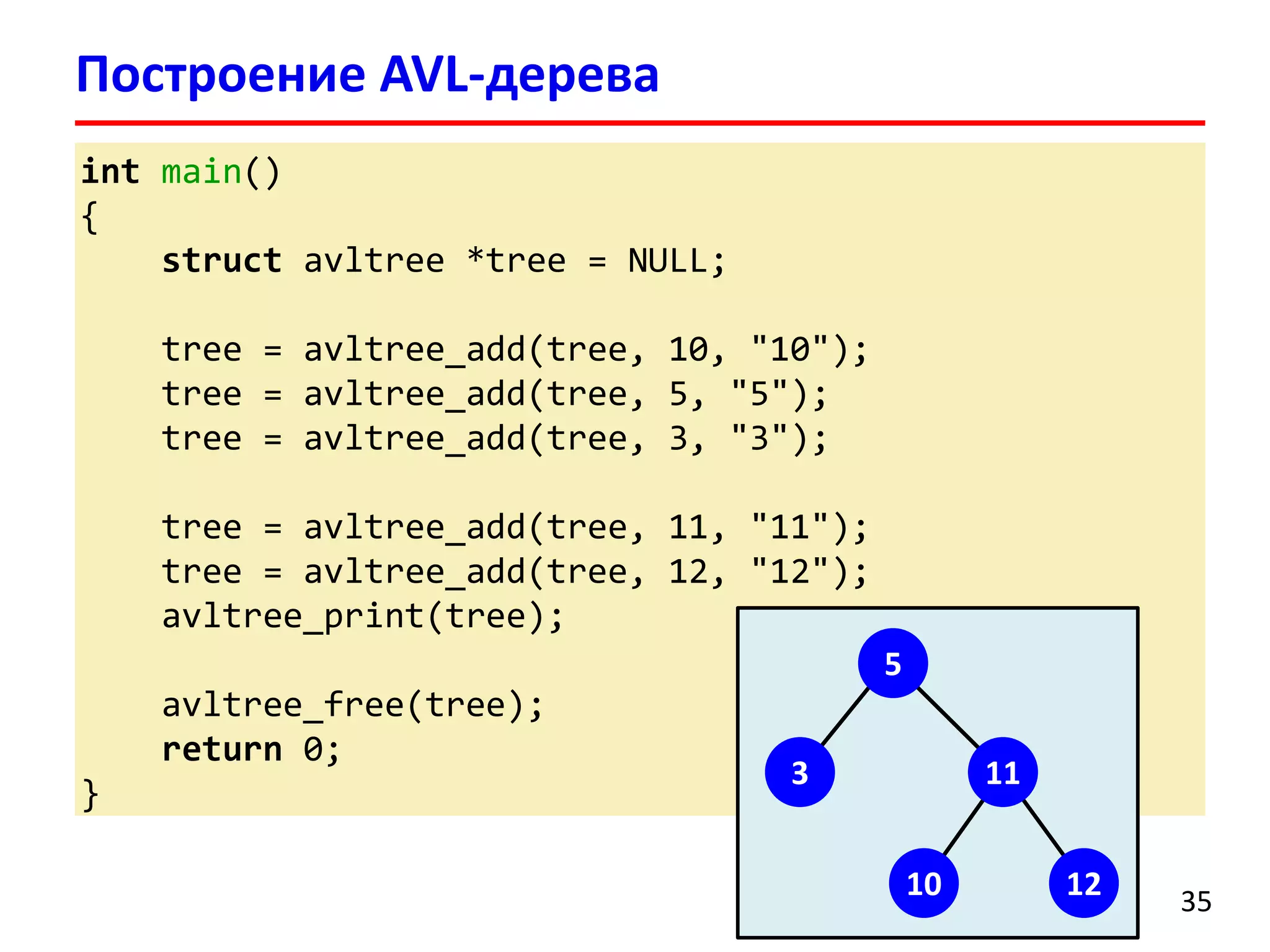
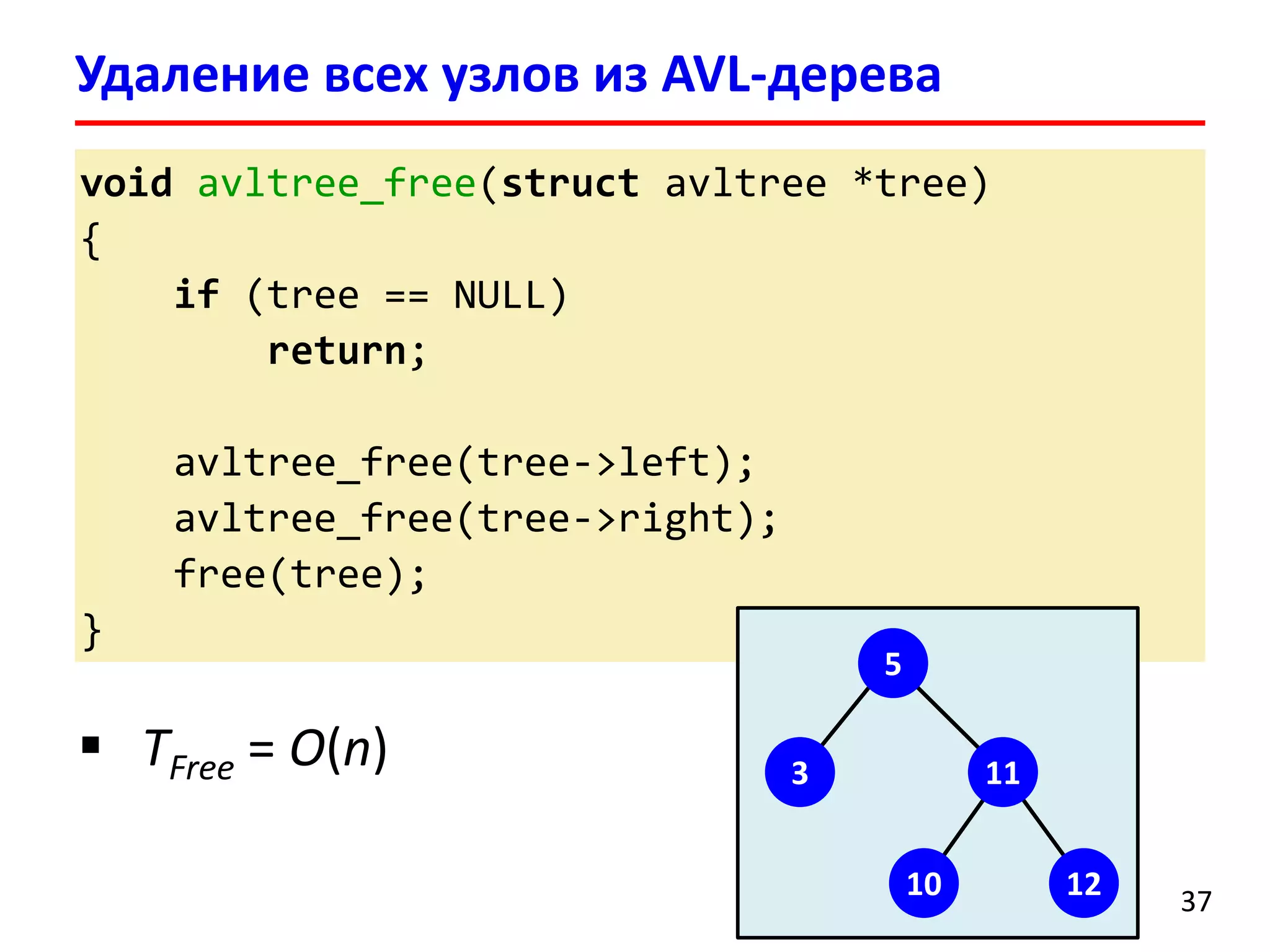
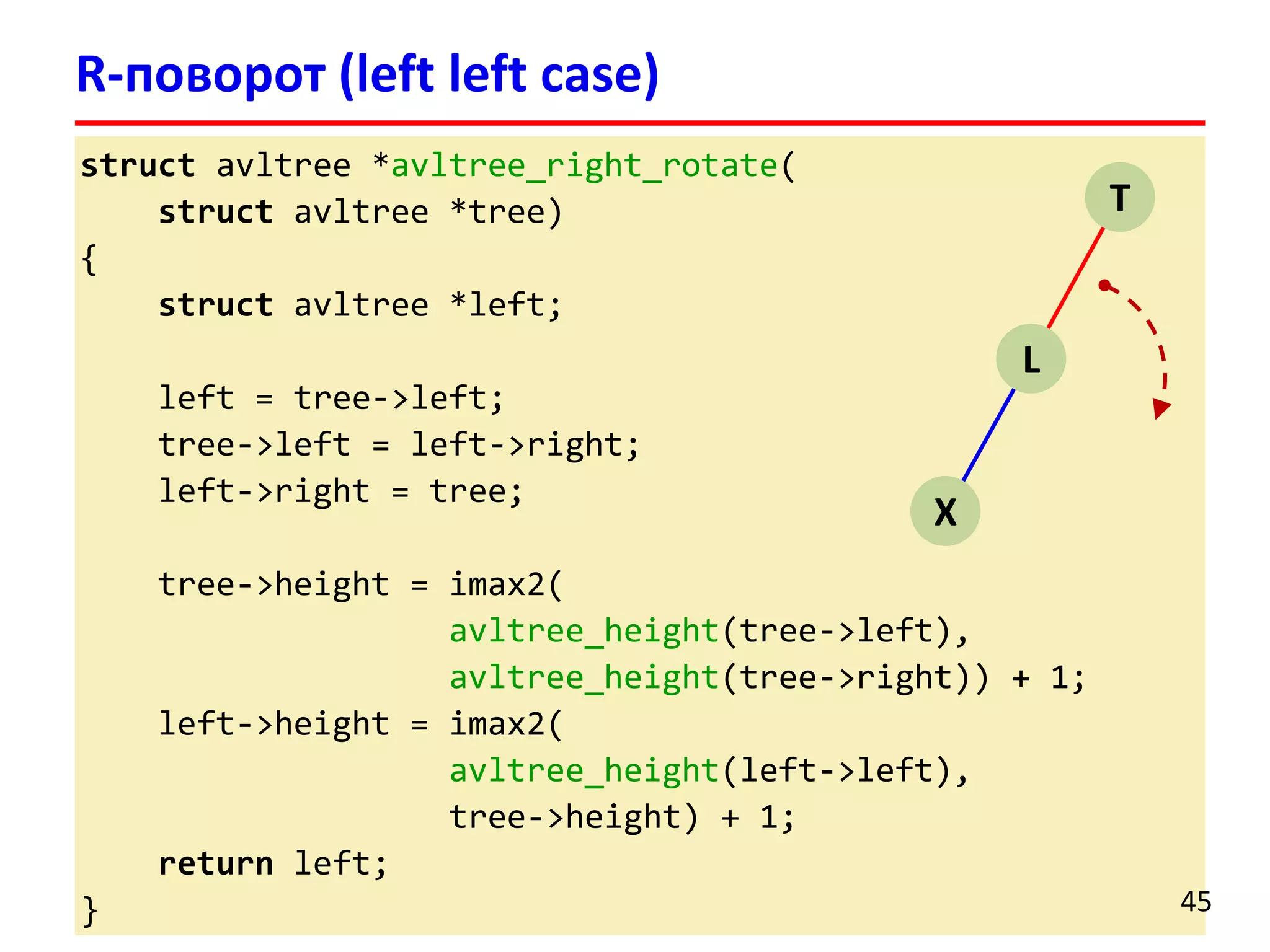
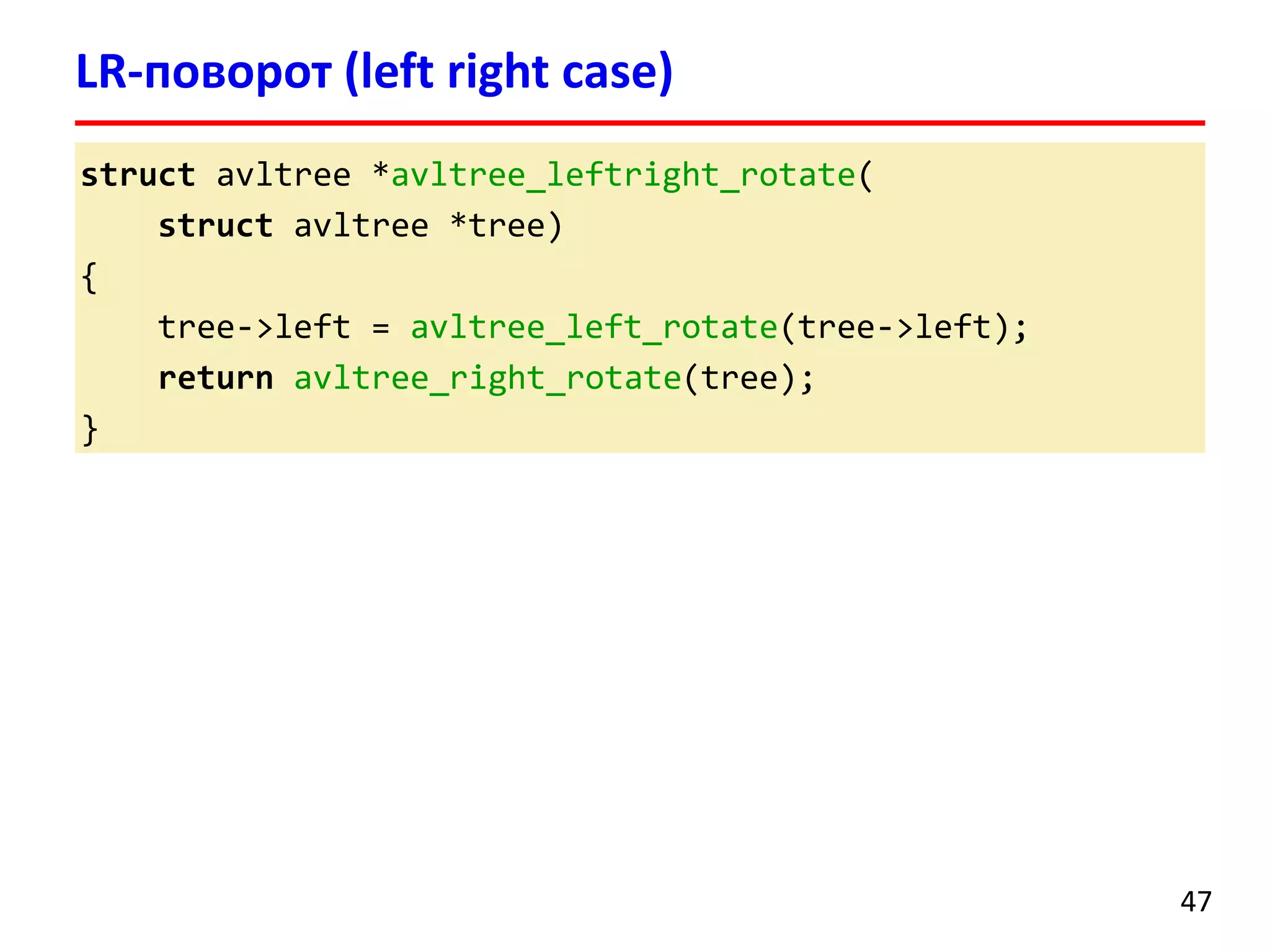
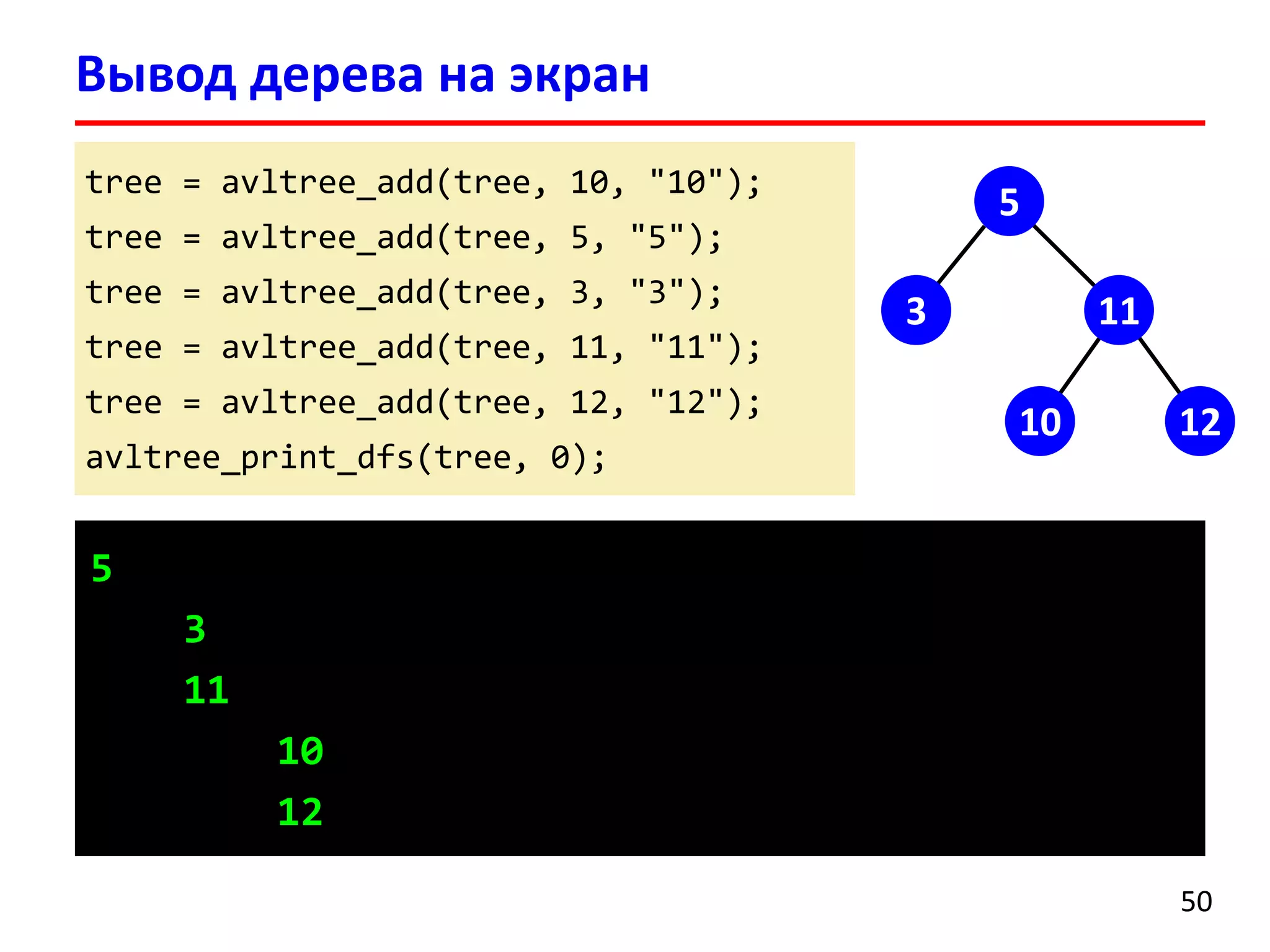
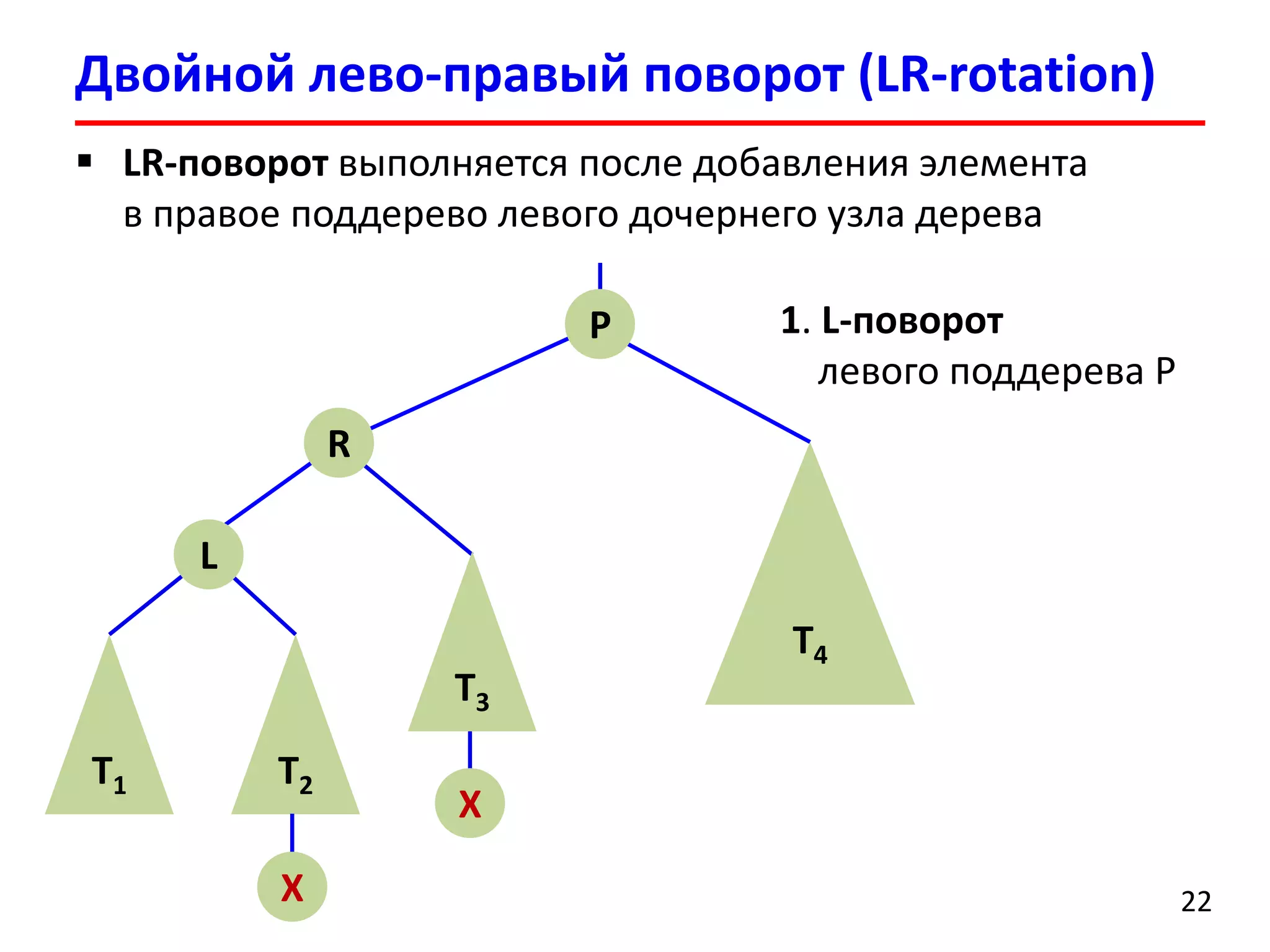
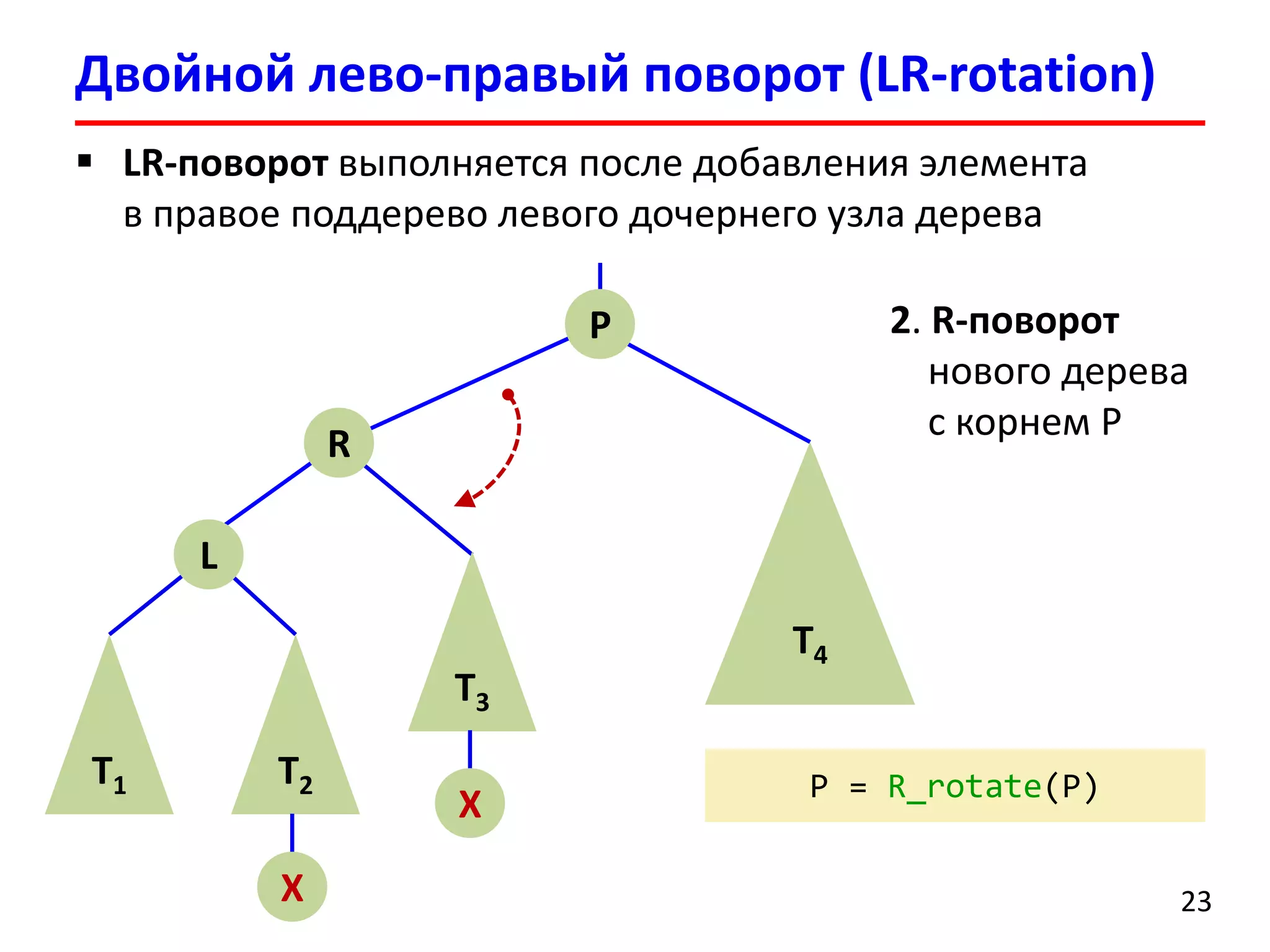
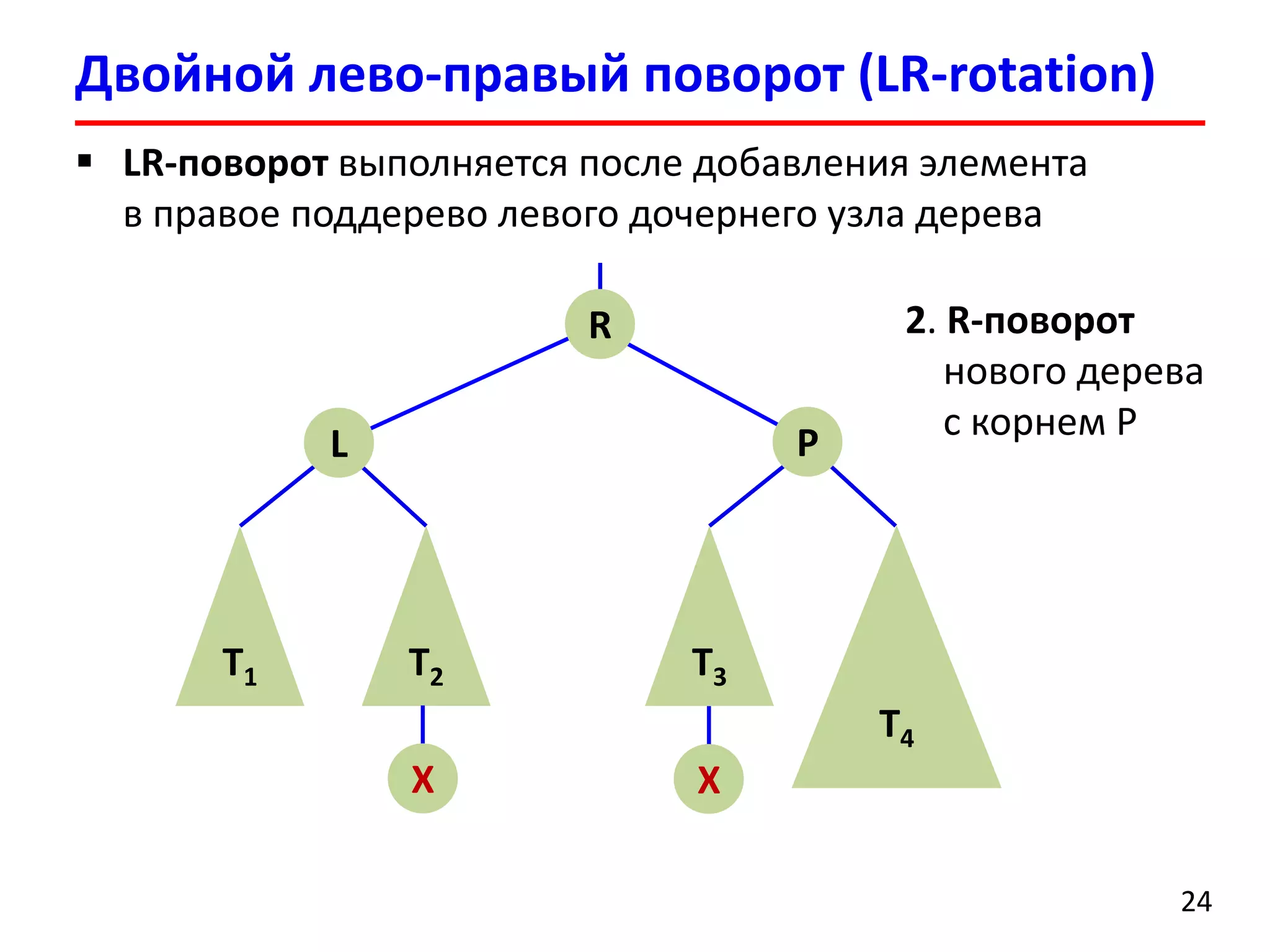
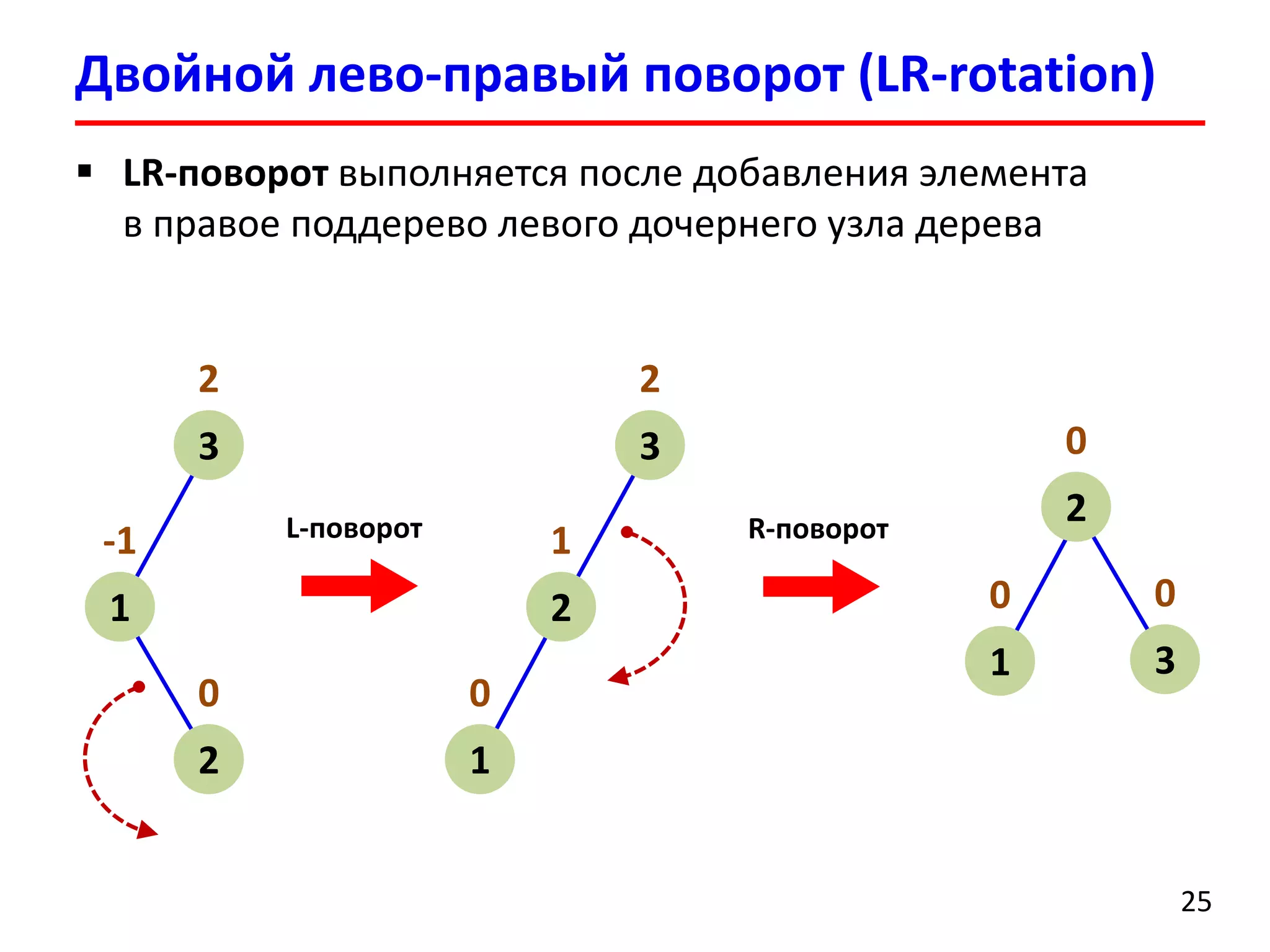
51. Удаление элемента выполняется аналогично добавлению
После удаления может нарушиться баланс нескольких родительских вершин
После удаления вершины может потребоваться порядка O(logn)поворотов поддеревьев
Удалениеэлемента
51
Вирт Н. Алгоритмы и структуры данных. –М.:Мир, 1989. [Глава 4.5, С. 272—286]

52. С каждым узлом АВЛ-дерева ассоциирован флаг deleted
При удалении узла находим его в дереве и устанавливаем флаг deleted= 1(реализуется за время O(logn))
При вставке нового узла с таким же ключом как и у удалённого элемента, устанавливаем у последнего флаг deleted= 0 (в поле данных копируем новое значение)
При достижении порогового значения количества узлов с флагом deleted= 1создаем новое АВЛ-деревосодержащее все не удалённые узлы (deleted= 0)
Поиск не удалённых элементов и их вставка в новое АВЛ-деревореализуется за время O(nlogn)
Ленивое удалениеэлементов (Lazy Deletion)
52

53. Литература
53
1.Левитин А.В. Алгоритмы: введение в разработку и анализ. –М.: Вильямс, 2006. –576 с.(С. 267-271)
2.Вирт Н. Алгоритмы и структуры данных. –М.: Мир, 1989. – 360 с.(С. 272-286)
3.Кнут Д. Искусство программирования, Том 3. Сортировка и поиск.–М.: Вильямс, 2007. –824 с.
4.AVL-деревья // Сайт RSDN.ru. – URL: http://www.rsdn.ru/article/alg/bintree/avl.xml
5.To Google:
“avltree” || “avltree ext:pdf” || “avltree ext:ppt”