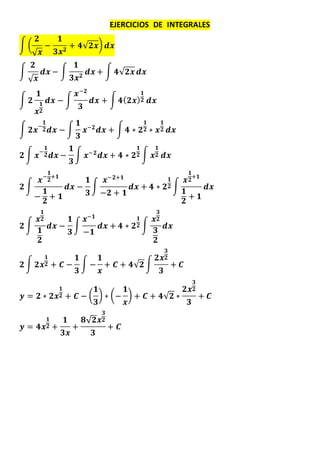More Related Content
Similar to Ejercicios de integrales
Similar to Ejercicios de integrales (15)
More from NILO ALBERTO BENAVIDES SOLIS
More from NILO ALBERTO BENAVIDES SOLIS (7)
Ejercicios de integrales
- 1. EJERCICIOS DE INTEGRALES
∫ (
𝟐
√ 𝒙
−
𝟏
𝟑𝒙 𝟐
+ 𝟒√𝟐𝒙) 𝒅𝒙
∫
𝟐
√ 𝒙
𝒅𝒙 − ∫
𝟏
𝟑𝒙 𝟐
𝒅𝒙 + ∫ 𝟒√𝟐𝒙 𝒅𝒙
∫ 𝟐
𝟏
𝒙
𝟏
𝟐
𝒅𝒙 − ∫
𝒙−𝟐
𝟑
𝒅𝒙 + ∫ 𝟒( 𝟐𝒙)
𝟏
𝟐 𝒅𝒙
∫ 𝟐𝒙
−
𝟏
𝟐 𝒅𝒙 − ∫
𝟏
𝟑
𝒙−𝟐
𝒅𝒙 + ∫ 𝟒 ∗ 𝟐
𝟏
𝟐 ∗ 𝒙
𝟏
𝟐 𝒅𝒙
𝟐 ∫ 𝒙
−
𝟏
𝟐 𝒅𝒙 −
𝟏
𝟑
∫ 𝒙−𝟐
𝒅𝒙 + 𝟒 ∗ 𝟐
𝟏
𝟐 ∫ 𝒙
𝟏
𝟐 𝒅𝒙
𝟐 ∫
𝒙−
𝟏
𝟐
+𝟏
−
𝟏
𝟐
+ 𝟏
𝒅𝒙 −
𝟏
𝟑
∫
𝒙−𝟐+𝟏
−𝟐 + 𝟏
𝒅𝒙 + 𝟒 ∗ 𝟐
𝟏
𝟐 ∫
𝒙
𝟏
𝟐
+𝟏
𝟏
𝟐
+ 𝟏
𝒅𝒙
𝟐 ∫
𝒙
𝟏
𝟐
𝟏
𝟐
𝒅𝒙 −
𝟏
𝟑
∫
𝒙−𝟏
−𝟏
𝒅𝒙 + 𝟒 ∗ 𝟐
𝟏
𝟐 ∫
𝒙
𝟑
𝟐
𝟑
𝟐
𝒅𝒙
𝟐 ∫ 𝟐𝒙
𝟏
𝟐 + 𝑪 −
𝟏
𝟑
∫ −
𝟏
𝒙
+ 𝑪 + 𝟒√𝟐 ∫
𝟐𝒙
𝟑
𝟐
𝟑
+ 𝑪
𝒚 = 𝟐 ∗ 𝟐𝒙
𝟏
𝟐 + 𝑪 − (
𝟏
𝟑
) ∗ (−
𝟏
𝒙
) + 𝑪 + 𝟒√𝟐 ∗
𝟐𝒙
𝟑
𝟐
𝟑
+ 𝑪
𝒚 = 𝟒𝒙
𝟏
𝟐 +
𝟏
𝟑𝒙
+
𝟖√ 𝟐𝒙
𝟑
𝟐
𝟑
+ 𝑪
- 2. ∫
(√ 𝒙 − 𝟐𝒙)
𝟐
√ 𝒙
𝒅𝒙
∫
(√ 𝒙)
𝟐
− 𝟐√ 𝒙( 𝟐𝒙) + ( 𝟐𝒙) 𝟐
√ 𝒙
𝒅𝒙
∫
𝒙 − 𝟒𝒙√ 𝒙 + 𝟒𝒙 𝟐
√ 𝒙
𝒅𝒙
∫
𝒙
√ 𝒙
−
𝟒𝒙√ 𝒙
√ 𝒙
+
𝟒𝒙 𝟐
√ 𝒙
𝒅𝒙
∫
𝒙
𝒙
𝟏
𝟐
− 𝟒𝒙 +
𝟒𝒙 𝟐
𝒙
𝟏
𝟐
𝒅𝒙
∫ ( 𝒙
𝟏
𝟐 − 𝟒𝒙 + 𝟒𝒙
𝟑
𝟐) 𝒅𝒙
∫ ( 𝒙
𝟏
𝟐) 𝒅𝒙 − ∫( 𝟒𝒙) 𝒅𝒙 + ∫( 𝟒𝒙
𝟑
𝟐) 𝒅𝒙
∫
𝒙
𝟏
𝟐
+𝟏
𝟏
𝟐
+ 𝟏
𝒅𝒙 − 𝟒 ∫
𝒙 𝟏+𝟏
𝟏 + 𝟏
𝒅𝒙 + 𝟒 ∫
𝒙
𝟑
𝟐
+𝟏
𝟑
𝟐
+ 𝟏
𝒅𝒙
∫
𝒙
𝟑
𝟐
𝟑
𝟐
𝒅𝒙 − 𝟒 ∫
𝒙 𝟐
𝟐
𝒅𝒙 + 𝟒 ∫
𝒙
𝟓
𝟐
𝟓
𝟐
𝒅𝒙
∫
𝟐𝒙
𝟑
𝟐
𝟑
+ 𝑪 − 𝟒 ∫
𝒙 𝟐
𝟐
+ 𝑪 + 𝟒 ∫
𝟐𝒙
𝟓
𝟐
𝟓
+ 𝑪
𝒚 =
𝟐𝒙
𝟑
𝟐
𝟑
− 𝟒 ∗
𝒙 𝟐
𝟐
+ 𝟒
𝟐𝒙
𝟓
𝟐
𝟓
+ 𝑪
𝒚 =
𝟐
𝟑
𝒙
𝟑
𝟐 − 𝟐𝒙 𝟐
+
𝟖
𝟓
𝒙
𝟓
𝟐 + 𝑪
- 3. ∫ ( 𝟒√𝟐𝒙 −
𝟏
𝟑𝒙 𝟐
+
𝟐
√ 𝒙
) 𝒅𝒙
∫ 𝟒( 𝟐𝒙)
𝟏
𝟐 𝒅𝒙 − ∫
𝒙−𝟐
𝟑
𝒅𝒙 + ∫
𝟐
𝒙
𝟏
𝟐
𝒅𝒙
∫ 𝟒 ∗ 𝟐
𝟏
𝟐( 𝒙)
𝟏
𝟐 𝒅𝒙 − ∫
𝟏
𝟑
𝒙−𝟐
𝒅𝒙 + ∫ 𝟐𝒙
−
𝟏
𝟐 𝒅𝒙
𝟒 ∗ 𝟐
𝟏
𝟐 ∫( 𝒙)
𝟏
𝟐 𝒅𝒙 −
𝟏
𝟑
∫ 𝒙−𝟐
𝒅𝒙 + 𝟐 ∫ 𝒙
−
𝟏
𝟐 𝒅𝒙
𝟒 ∗ 𝟐
𝟏
𝟐 ∫
( 𝒙)
𝟏
𝟐
+𝟏
𝟏
𝟐
+ 𝟏
+ 𝒄 −
𝟏
𝟑
∫
𝒙−𝟐+𝟏
−𝟐 + 𝟏
+ 𝒄 + 𝟐 ∫
𝒙−
𝟏
𝟐
+𝟏
−
𝟏
𝟐
+ 𝟏
+ 𝒄
𝟒 ∗ √𝟐 ∫
( 𝒙)
𝟑
𝟐
𝟑
𝟐
+ 𝒄 −
𝟏
𝟑
∫
𝒙−𝟏
−𝟏
+ 𝒄 + 𝟐 ∫
𝒙
𝟏
𝟐
𝟏
𝟐
+ 𝒄
𝟒 ∗ √𝟐 ∫
𝟐( 𝒙)
𝟑
𝟐
𝟑
+ 𝒄 −
𝟏
𝟑
∫ −
𝟏
𝒙
+ 𝒄 + 𝟐 ∫ 𝟐𝒙
𝟏
𝟐 + 𝒄
𝒚 = 𝟒√𝟐 ∗
𝟐( 𝒙)
𝟑
𝟐
𝟑
+
𝟏
𝟑
∗
𝟏
𝒙
+ 𝟐 ∗ 𝟐𝒙
𝟏
𝟐 + 𝒄
𝒚 =
𝟖√ 𝟐
𝟑
( 𝒙)
𝟑
𝟐 +
𝟏
𝟑𝒙
+ 𝟒√ 𝒙 + 𝒄
- 4. ∫
(√ 𝒙 − 𝟐𝒙)
𝟐
√ 𝒙
𝒅𝒙
∫ (
(√ 𝒙)
𝟐
− 𝟐√ 𝒙( 𝟐𝒙) + ( 𝟐𝒙) 𝟐
√ 𝒙
) 𝒅𝒙
∫ (
𝒙 − 𝟒𝒙√ 𝒙 + 𝟒𝒙 𝟐
√ 𝒙
) 𝒅𝒙
∫ (
𝒙
√ 𝒙
−
𝟒𝒙√ 𝒙
√ 𝒙
+
𝟒𝒙 𝟐
√ 𝒙
) 𝒅𝒙
∫ (
𝒙
𝒙
𝟏
𝟐
− 𝟒𝒙 +
𝟒𝒙 𝟐
𝒙
𝟏
𝟐
) 𝒅𝒙
∫ ( 𝒙 ∗ 𝒙
−
𝟏
𝟐 − 𝟒𝒙 + 𝟒𝒙 𝟐
∗ 𝒙
−
𝟏
𝟐) 𝒅𝒙
∫ ( 𝒙
𝟏
𝟐 − 𝟒𝒙 + 𝟒𝒙
𝟑
𝟐) 𝒅𝒙
∫ 𝒙
𝟏
𝟐 𝒅𝒙 − ∫ 𝟒𝒙𝒅𝒙 + ∫ 𝟒𝒙
𝟑
𝟐 𝒅𝒙
∫
𝒙
𝟏
𝟐
+𝟏
𝟏
𝟐
+ 𝟏
+ 𝒄 − 𝟒 ∫ 𝒙 𝒅𝒙 + 𝟒 ∫ 𝒙
𝟑
𝟐 𝒅𝒙
∫
𝒙
𝟑
𝟐
𝟑
𝟐
+ 𝒄 − 𝟒 ∫
𝒙 𝟏+𝟏
𝟏 + 𝟏
+ 𝒄 + 𝟒 ∫
𝒙
𝟑
𝟐
+𝟏
𝟑
𝟐
+ 𝟏
+ 𝒄
∫
𝟐𝒙
𝟑
𝟐
𝟑
+ 𝒄 − 𝟒 ∫
𝒙 𝟐
𝟐
+ 𝒄 + 𝟒 ∫
𝒙
𝟓
𝟐
𝟓
𝟐
+ 𝒄
∫
𝟐𝒙
𝟑
𝟐
𝟑
+ 𝒄 − 𝟒 ∫
𝒙 𝟐
𝟐
+ 𝒄 + 𝟒 ∫
𝟐𝒙
𝟓
𝟐
𝟓
+ 𝒄
𝒚 =
𝟐𝒙
𝟑
𝟐
𝟑
− 𝟒 ∗
𝒙 𝟐
𝟐
+ 𝟒 ∗
𝟐𝒙
𝟓
𝟐
𝟓
+ 𝒄
- 5. 𝒚 =
𝟐
𝟑
𝒙
𝟑
𝟐 − 𝟐𝒙 𝟐
+
𝟖
𝟓
𝒙
𝟓
𝟐 + 𝒄
INTEGRALES DE FUNCIONES DERIVADAS TRASCENDENTES
REGLA 1
∫
𝟏
𝒙
𝒅𝒙 𝒚 = 𝐥𝐧| 𝒙| + 𝒄
∫
𝟑
𝒙
𝒅𝒙
∫ 𝟑
𝟏
𝒙
𝒅𝒙
𝟑 ∫
𝟏
𝒙
𝒅𝒙
𝟑 ∫ 𝐥𝐧| 𝒙| + 𝒄
𝒚 = 𝟑 𝐥𝐧| 𝒙| + 𝒄
∫
𝟏
𝟓𝒙
𝒅𝒙
∫
𝟏
𝟓
∗
𝟏
𝒙
𝒅𝒙
𝟏
𝟓
∫
𝟏
𝒙
𝒅𝒙
𝟏
𝟓
∫ 𝐥𝐧| 𝒙| + 𝒄
𝒚 =
𝟏
𝟓
𝐥𝐧| 𝒙| + 𝒄
REGLA 2
∫ 𝒆 𝒙
𝒅𝒙 𝒚 = 𝒆 𝒙
+ 𝒄
- 6. ∫ 𝟏𝟏𝒆 𝒙
𝒅𝒙
𝟏𝟏 ∫ 𝒆 𝒙
𝒅𝒙
𝟏𝟏 ∫ 𝒆 𝒙
+ 𝒄
𝒚 = 𝟏𝟏𝒆 𝒙
+ 𝒄
∫
𝒆 𝒙
𝟐𝟎
𝒅𝒙
∫
𝟏
𝟐𝟎
𝒆 𝒙
𝒅𝒙
𝟏
𝟐𝟎
∫ 𝒆 𝒙
𝒅𝒙
𝟏
𝟐𝟎
∫ 𝒆 𝒙
+ 𝒄
𝒚 =
𝟏
𝟐𝟎
𝒆 𝒙
+ 𝒄
REGLA 3
∫( 𝒔𝒆𝒏 𝒙) 𝒅𝒙 𝒚 = −𝒄𝒐𝒔 𝒙 + 𝒄
REGLA 4
∫( 𝒄𝒐𝒔 𝒙) 𝒅𝒙 𝒚 = 𝒔𝒆𝒏 𝒙 + 𝒄
REGLA 5
∫ (
𝟏
𝒄𝒐𝒔 𝟐 𝒙
) 𝒅𝒙 𝒚 = 𝒕𝒈 𝒙 + 𝒄
REGLA 6
∫ (
𝟏
𝒔𝒆𝒏 𝟐 𝒙
) 𝒅𝒙 𝒚 = 𝒄𝒕𝒈 𝒙 + 𝒄
- 7. REGLA 7
∫ (
𝟏
√ 𝟏 − 𝒙 𝟐
) 𝒅𝒙 𝒚 = 𝒂𝒓𝒄 𝒔𝒆𝒏 𝒙 + 𝒄 𝒚 = −𝒂𝒓𝒄 𝒄𝒐𝒔 𝒙 + 𝒄
REGLA 8
∫ (
𝟏
𝟏 + 𝒙 𝟐
) 𝒅𝒙 𝒚 = 𝒂𝒓𝒄 𝒕𝒈 𝒙 + 𝒄 𝒚 = −𝒂𝒓𝒄 𝒄𝒕𝒈 𝒙 + 𝒄
REGLA 9
∫ 𝒂 𝒙
𝒅𝒙 a es una constante y condición a = 1
𝒚 =
𝒂 𝒙
𝐥𝐧 𝒂
+ 𝒄
∫ 𝟏𝟕 𝒙
𝒅𝒙
𝒚 =
𝟏𝟕 𝒙
𝐥𝐧 𝟏𝟕
+ 𝒄
∫ 𝟐( 𝟖 𝒙) 𝒅𝒙
𝟐 ∫( 𝟖 𝒙) 𝒅𝒙
𝟐 ∫ (
𝟖 𝒙
𝒍𝒏 𝟖
) + 𝒄
𝒚 = 𝟐
𝟖 𝒙
𝒍𝒏 𝟖
+ 𝒄
∫ (
𝟓 𝒙
𝟑
) 𝒅𝒙
∫
𝟏
𝟑
𝟓 𝒙
𝒅𝒙
𝟏
𝟑
∫ 𝟓 𝒙
𝒅𝒙
- 8. 𝟏
𝟑
∫
𝟓 𝒙
𝒍𝒏 𝟓
+ 𝒄
𝒚 =
𝟏
𝟑
∗
𝟓 𝒙
𝒍𝒏 𝟓
+ 𝒄 𝒚 =
𝟓 𝒙
𝟑𝒍𝒏 𝟓
+ 𝒄
INTEGRALES POR CAMBIO DE VARIABLE O SUSTITUCIÓN DE PRODUCTOS
∫( 𝒙 + 𝟑)√𝒙 − 𝟒 𝒅𝒙
𝒖 = 𝒙 − 𝟒 𝒅𝒆𝒔𝒑𝒆𝒋𝒂𝒓 𝒍𝒂 𝒙 𝒙 = 𝒖 + 𝟒
Derivar
𝒅𝒖
𝒅𝒙
= 𝟏 𝒅𝒖 = 𝒅𝒙
∫( 𝒖 + 𝟒 + 𝟑)√ 𝒖 𝒅𝒖
∫( 𝒖 + 𝟕) 𝒖
𝟏
𝟐 𝒅𝒖
∫ ( 𝒖 ∗ 𝒖
𝟏
𝟐 + 𝟕𝒖
𝟏
𝟐) 𝒅𝒖
∫ ( 𝒖
𝟑
𝟐 + 𝟕𝒖
𝟏
𝟐) 𝒅𝒖
∫ 𝒖
𝟑
𝟐 𝒅𝒖 + ∫ 𝟕𝒖
𝟏
𝟐 𝒅𝒖
∫
𝒖
𝟑
𝟐
+𝟏
𝟑
𝟐
+ 𝟏
𝒅𝒖 + 𝟕 ∫
𝒖
𝟏
𝟐
+𝟏
𝟏
𝟐
+ 𝟏
𝒅𝒖
∫
𝒖
𝟓
𝟐
𝟓
𝟐
+ 𝒄 + 𝟕 ∫
𝒖
𝟑
𝟐
𝟑
𝟐
+ 𝒄
∫
𝟐𝒖
𝟓
𝟐
𝟓
+ 𝒄 + 𝟕 ∫
𝟐𝒖
𝟑
𝟐
𝟑
+ 𝒄
- 9. 𝒚 =
𝟐
𝟓
𝒖
𝟓
𝟐 + 𝟕 ∗
𝟐
𝟑
𝒖
𝟑
𝟐 + 𝒄
𝒚 =
𝟐
𝟓
( 𝒙 − 𝟒)
𝟓
𝟐 +
𝟏𝟒
𝟑
( 𝒙 − 𝟒)
𝟑
𝟐 + 𝒄
∫( 𝒙 𝟐
+ 𝟐𝒙 − 𝟓) 𝟔( 𝒙 + 𝟏) 𝒅𝒙
𝒖 = 𝒙 𝟐
+ 𝟐𝒙 − 𝟓
Derivar
𝒅𝒖
𝒅𝒙
= 𝟐𝒙 + 𝟐
𝒅𝒖
𝒅𝒙
= 𝟐( 𝒙 + 𝟏)
𝒅𝒖
𝟐( 𝒙 + 𝟏)
= 𝒅𝒙
∫( 𝒖) 𝟔( 𝒙 + 𝟏)
𝒅𝒖
𝟐( 𝒙 + 𝟏)
∫( 𝒖) 𝟔
𝟏
𝟐
𝒅𝒖
𝟏
𝟐
∫
( 𝒖) 𝟔+𝟏
𝟔 + 𝟏
+ 𝒄
𝟏
𝟐
∫
( 𝒖) 𝟕
𝟕
+ 𝒄
𝒚 =
𝟏
𝟐
∗
𝟏
𝟕
𝒖 𝟕
+ 𝒄
𝒚 =
𝟏
𝟏𝟒
( 𝒙 𝟐
+ 𝟐𝒙 − 𝟓) 𝟕
+ 𝒄
∫
𝒙 𝟑
√ 𝒙 𝟐 + 𝟏
𝒅𝒙
𝒖 𝟐
= 𝒙 𝟐
+ 𝟏
𝒖 𝟐
= 𝒙 𝟐
+ 𝟏 𝒙 𝟐
= 𝒖 𝟐
− 𝟏 𝒙 = √ 𝒖 𝟐 − 𝟏
𝒖 = √ 𝒙 𝟐 + 𝟏
2 𝑢2−1
𝑑𝑢 = (2𝑥) 𝑑𝑥
2 𝑢𝑑𝑢 = (2𝑥) 𝑑𝑥
2 𝑢
(2𝑥)
𝑑𝑢 = 𝑑𝑥
𝑢
√ 𝒖 𝟐−𝟏
𝑑𝑢 = 𝑑𝑥
- 10. Regla de derivación de una función elevada a una potencia
𝒚 = ( 𝒙 𝟐
+ 𝟏) 𝟐
𝒖 = ( 𝒙 𝟐
+ 𝟏)
𝒚 = 𝟐( 𝒙 𝟐
+ 𝟏) 𝟐−𝟏
𝒅( 𝒙 𝟐
+ 𝟏)
𝒚 = 𝟐𝒖 𝟐−𝟏
𝒅𝒖
∫
𝒙 𝟑
√ 𝒙 𝟐 + 𝟏
𝒅𝒙
∫
(√ 𝒖 𝟐 − 𝟏)
𝟑
𝒖
∗
𝑢
√ 𝒖 𝟐 − 𝟏
𝑑𝑢
∫
(√ 𝒖 𝟐 − 𝟏)
𝟑
√ 𝒖 𝟐 − 𝟏
𝑑𝑢
∫ (√ 𝒖 𝟐 − 𝟏)
𝟐
𝑑𝑢
∫( 𝒖 𝟐
− 𝟏) 𝑑𝑢
∫ 𝑢2
𝑑𝑢 − ∫ 𝑑𝑢
∫
𝑢2+1
2 + 1
+ 𝑐 − 𝑢 + 𝑐
∫
𝑢3
3
− 𝑢 + 𝑐
𝑦 =
1
3
𝑢3
− 𝑢 + 𝑐
𝑦 =
1
3
(√ 𝒙 𝟐 + 𝟏)
3
− √ 𝒙 𝟐 + 𝟏 + 𝑐
- 11. ∫
𝒅𝒙
( 𝒙 − 𝟐)√ 𝒙 + 𝟐
DESPEJE 𝒖 𝟐
= 𝒙 + 𝟐 𝒙 = 𝒖 𝟐
− 𝟐 𝒖 = √ 𝒙 + 𝟐
DERIVACIÓN 𝟐𝒖 𝒅𝒖 = 𝒅𝒙
∫
𝟐𝒖
( 𝒖 𝟐 − 𝟐 − 𝟐) 𝒖
𝒅𝒖
∫
𝟐
𝒖 𝟐 − 𝟒
𝒅𝒖
𝟐
𝒖 𝟐 − 𝟒
=
𝟐
𝒖 𝟐 − 𝟒
=
𝑨
( 𝒖 − 𝟐)
+
𝑩
( 𝒖 + 𝟐)
𝟐 =
𝑨( 𝒖 𝟐
− 𝟒)
( 𝒖 − 𝟐)
+
𝑩( 𝒖 𝟐
− 𝟒)
( 𝒖 + 𝟐)
𝟐 =
𝑨( 𝒖 + 𝟐)( 𝒖 − 𝟐)
( 𝒖 − 𝟐)
+
𝑩( 𝒖 + 𝟐)( 𝒖 − 𝟐)
( 𝒖 + 𝟐)
𝟐 = 𝑨( 𝒖 + 𝟐) + 𝑩( 𝒖 − 𝟐)
𝒖 + 𝟐 = 𝟎 𝒖 − 𝟐 = 𝟎
𝒖 = −𝟐 𝒖 = +𝟐
𝟐 = 𝑨(−𝟐 + 𝟐) + 𝑩(−𝟐 − 𝟐)
𝟐 = 𝟎 + 𝑩(−𝟐 − 𝟐)
𝟐 = −𝟒𝑩
𝟐
−𝟒
= 𝑩
- 12. 𝑩 = −
𝟏
𝟐
𝟐 = 𝑨( 𝟐 + 𝟐) + 𝑩( 𝟐 − 𝟐)
𝟐 = 𝑨( 𝟐 + 𝟐) + 𝟎
𝟐 = 𝟒𝑨
𝑨 =
𝟏
𝟐
∫
𝟏
𝟐
( 𝒖 − 𝟐)
+
−
𝟏
𝟐
( 𝒖 + 𝟐)
𝒅𝒖
∫
𝟏
𝟐
𝟏
( 𝒖 − 𝟐)
−
𝟏
𝟐
𝟏
( 𝒖 + 𝟐)
𝒅𝒖
𝟏
𝟐
∫
𝟏
( 𝒖 − 𝟐)
𝒅𝒖 −
𝟏
𝟐
∫
𝟏
( 𝒖 + 𝟐)
𝒅𝒖
𝟏
𝟐
∫ 𝐥𝐧| 𝒖 − 𝟐| + 𝒄 −
𝟏
𝟐
∫ 𝐥𝐧| 𝒖 + 𝟐| + 𝒄
𝒚 =
𝟏
𝟐
𝐥𝐧| 𝒖 − 𝟐| −
𝟏
𝟐
𝐥𝐧| 𝒖 + 𝟐| + 𝒄
𝒚 =
𝟏
𝟐
𝐥𝐧|√𝒙 + 𝟐 − 𝟐| −
𝟏
𝟐
𝐥𝐧|√𝒙 + 𝟐 + 𝟐| + 𝒄
∫
𝒙 𝟐
√ 𝟏 + 𝟐𝒙𝟑
𝒅𝒙
𝒖 = √ 𝟏 + 𝟐𝒙𝟑
DESPEJE
𝒖 𝟑
= 𝟏 + 𝟐𝒙
𝒖 𝟑−𝟏
𝟐
= 𝒙
- 13. DERIVAMOS
𝑢3
= 1 + 2𝑥
3𝑢3−1
𝑑𝑢 = 2𝑑𝑥
3𝑢2
𝑑𝑢 = 2𝑑𝑥
3𝑢2
2
𝑑𝑢 = 𝑑𝑥
REEMPLAZAR
∫
(
𝑢3
− 1
2
)
2
𝑢
3𝑢2
2
𝑑𝑢
∫ (
𝑢3
− 1
2
)
2
3
2
𝑢 𝑑𝑢
3
2
∫ (
𝑢3
− 1
2
)
2
𝑢 𝑑𝑢
3
2
∫
( 𝑢3
− 1)2
22
𝑢 𝑑𝑢
3
2
∫
𝑢6
− 2𝑢3
+ 1
4
𝑢 𝑑𝑢
3
2
∗
1
4
∫( 𝑢6
− 2𝑢3
+ 1) 𝑢 𝑑𝑢
3
8
∫( 𝑢6
− 2𝑢3
+ 1) 𝑢 𝑑𝑢
3
8
∫( 𝑢7
− 2𝑢4
+ 𝑢) 𝑑𝑢
∫ 𝑥(√1 + 𝑥) 𝑑𝑥
DESPEJAR
INTEGRAMOS EL POLINOMIO
3
8
∫( 𝑢7
− 2𝑢4
+ 𝑢) 𝑑𝑢
3
8
(∫ 𝑢7
𝑑𝑢 − ∫2𝑢4
𝑑𝑢 + ∫ 𝑢 𝑑𝑢)
3
8
(∫
𝑢7+1
7 + 1
𝑑𝑢 − 2∫
𝑢4+1
4 + 1
𝑑𝑢 + ∫
𝑢1+1
1 + 1
𝑑𝑢)
3
8
(∫
𝑢8
8
+ 𝑐 − 2 ∫
𝑢5
5
+ 𝑐 + ∫
𝑢2
2
+ 𝑐)
3
8
(∫
1
8
𝑢8
+ 𝑐 − 2 ∫
1
5
𝑢5
+ 𝑐 + ∫
1
2
𝑢2
+ 𝑐)
𝑦 =
3
8
(
1
8
𝑢8
− 2 ∗
1
5
𝑢5
+
1
2
𝑢2
) + 𝒄
𝑦 =
3
64
𝑢8
−
3
20
𝑢5
+
3
16
𝑢2
+ 𝒄
REEMPLAZAMOS LA VARIABLE U
𝑦 =
3
64
( √1+ 2𝑥
3
)
8
−
3
20
( √1+ 2𝑥
3
)
5
+
3
16
(√1 + 2𝑥
3
)
2
+ 𝒄
- 14. 𝑢 = √1 + 𝑥
𝑢2
= 1 + 𝑥 𝑥 = 𝑢2
− 1
DERIVAMOS
𝑢2
= 1 + 𝑥
2𝑢 𝑑𝑢 = 𝑑𝑥
REEMPLAZAMOS
∫ 𝑥(√1 + 𝑥)𝑑𝑥
∫( 𝑢2
− 1) 𝑢 2𝑢 𝑑𝑢
2∫( 𝑢2
− 1) 𝑢2
𝑑𝑢
2∫( 𝑢4
− 𝑢2) 𝑑𝑢
INTEGRAMOS
2∫( 𝑢4
− 𝑢2) 𝑑𝑢
2∫ 𝑢4
𝑑𝑢 − ∫ 𝑢2
𝑑𝑢
2(∫
𝑢4+1
4 + 1
𝑑𝑢 − ∫
𝑢2+1
2 + 1
𝑑𝑢)
2(∫
𝑢5
5
+ 𝑐 − ∫
𝑢3
3
+ 𝑐)
2(∫
1
5
𝑢5
+ 𝑐 − ∫
1
3
𝑢3
+ 𝑐)
𝑦 = 2 (
1
5
𝑢5
−
1
3
𝑢3
) + 𝑐
𝑦 =
2
5
𝑢5
−
2
3
𝑢3
+ 𝑐
REEMPLAZAMOS LA VARIABLE U
𝑦 =
2
5
𝑢5
−
2
3
𝑢3
+ 𝑐
𝑦 =
2
5
(√1 + 𝑥)
5
−
2
3
(√1 + 𝑥)
3
+ 𝑐
- 15. ∫
𝑒4𝑥
+ 3
𝑒3𝑥
𝑢 = 𝑒 𝑥
DERIVAMOS
𝑢 = 𝑒 𝑥
𝑑𝑢 = 𝑒 𝑥
𝑑𝑥
𝑑𝑢
𝑒 𝑥 = 𝑑𝑥
𝑑𝑢
𝑢
= 𝑑𝑥
REEMPLAZAR
∫
𝑒4𝑥
+ 3
𝑒3𝑥
𝑑𝑥
∫
𝑢4
+ 3
𝑢3
∗
𝑑𝑢
𝑢
∫
𝑢4
+ 3
𝑢4
𝑑𝑢
∫ (
𝑢4
𝑢4
+
3
𝑢4
) 𝑑𝑢
∫(1 + 3𝑢−4) 𝑑𝑢
integramos
∫(1 + 3𝑢−4) 𝑑𝑢
∫ 𝑑𝑢 + ∫ 3𝑢−4
𝑑𝑢
∫ 𝑢 + 𝑐 + 3 ∫
𝑢−4+1
−4 + 1
𝑑𝑢
∫ 𝑢 + 𝑐 + 3 ∫
𝑢−4+1
−4 + 1
𝑑𝑢
∫ 𝑢 + 𝑐 + 3 ∫
𝑢−3
−3
+ 𝑐
𝑦 = 𝑢 + 3
𝑢−3
−3
+ 𝑐
𝑦 = 𝑢 −
1
𝑢3
+ 𝑐
𝑦 = 𝑒 𝑥
−
1
𝑒3𝑥
+ 𝑐
- 16. ∫
1 + 𝑒 𝑥
1 − 𝑒 𝑥
𝑑𝑥
𝑢 = 𝑒 𝑥
𝑑𝑢 = 𝑒 𝑥
𝑑𝑥
𝑑𝑢
𝑒 𝑥 = 𝑑𝑥
𝑑𝑢
𝑢
= 𝑑𝑥
∫
1 + 𝑒 𝑥
1 − 𝑒 𝑥
𝑑𝑥
∫
1 + 𝑢
1 − 𝑢
∗
𝑑𝑢
𝑢
∫
1 + 𝑢
𝑢(1 − 𝑢)
𝑑𝑢
1+𝑢
𝑢(1−𝑢)
=
(−)1+𝑢
𝑢(1−𝑢)(−)
=
−𝑢−1
𝑢( 𝑢−1)
−𝑢 − 1
𝑢( 𝑢 − 1)
=
𝐴
𝑢
+
𝐵
( 𝑢 − 1)
−𝑢 − 1 =
𝐴𝑢( 𝑢 − 1)
𝑢
+
𝐵𝑢( 𝑢 − 1)
( 𝑢 − 1)
−𝑢 − 1 = 𝐴( 𝑢 − 1) + 𝐵𝑢
𝑢 − 1 = 0 𝑢 = 0
𝑢 = 1
−1 − 1 = 𝐴(1 − 1) + 𝐵1 −0 − 1 = 𝐴(0 − 1) + 𝐵0
−2 = 𝐵 −1 = −𝐴 1 = 𝐴
∫
𝐴
𝑢
+
𝐵
( 𝑢 − 1)
𝑑𝑢
∫
1
𝑢
+
−2
( 𝑢 − 1)
𝑑𝑢
∫
1
𝑢
− 2 ∫
1
( 𝑢 − 1)
𝑑𝑢
∫ 𝑙𝑛| 𝑢| + 𝑐 − 2 ∫ 𝑙𝑛| 𝑢 − 1| + 𝑐
- 17. 𝑦 = 𝑙𝑛| 𝑢| − 2𝑙𝑛| 𝑢 − 1| + 𝑐
𝑦 = 𝑙𝑛| 𝑒 𝑥| − 2𝑙𝑛| 𝑒 𝑥
− 1| + 𝑐
∫
1
( 𝑥 + 1)√ 𝑥
𝑑𝑥
𝑢 = √ 𝑥
Despejar 𝑢2
= 𝑥 Derivar 2𝑢 𝑑𝑢 = 𝑑𝑥
Reemplazar
∫
1
( 𝑢2 + 1) 𝑢
2𝑢 𝑑𝑢
∫ 2
1
( 𝑢2 + 1)
𝑑𝑢
2 ∫
1
( 𝑢2 + 1)
𝑑𝑢
2 ∫
1
( 𝑢2 + 1)
𝑑𝑢
2 ∫ 𝑎𝑟𝑐 𝑡𝑔 𝑢 + 𝑐
2 ∫ 𝑎𝑟𝑐 𝑡𝑔 𝑢 + 𝑐
𝑦 = 𝑎𝑟𝑐 𝑡𝑔 𝑢 + 𝑐
𝑦 = 𝑎𝑟𝑐 𝑡𝑔 √ 𝑥 + 𝑐
∫
𝑒3𝑥
1 + 𝑒3𝑥
𝑑𝑥
𝑢 = 𝑒 𝑥
- 18. 𝑑𝑢 = 𝑒 𝑥
𝑑𝑥
𝑑𝑢
𝑒 𝑥 = 𝑑𝑥
𝑑𝑢
𝑢
= 𝑑𝑥
∫
𝑒3𝑥
1 + 𝑒3𝑥
𝑑𝑥
∫
𝑢3
1 + 𝑢3
∗
𝑑𝑢
𝑢
∫
𝑢3
𝑢(1+𝑢3)
𝑑𝑢 ∫
𝑢2
(1+𝑢3)
𝑑𝑢
𝑑𝑦
𝑑𝑥
= 1 + 𝑢3 𝑑𝑦
𝑑𝑢
= 3𝑢2
𝑑𝑦 = 3𝑢2
𝑑𝑢
𝑑𝑦
3𝑢2 = 𝑑𝑢
∫
𝑢2
(1 + 𝑢3)
∗
𝑑𝑢
3𝑢2
∫
1
(1 + 𝑢3)
∗
𝑑𝑢
3
∫
1
3
1
(1 + 𝑢3)
𝑑𝑢
1
3
∫
1
(1 + 𝑢3)
𝑑𝑢
1
3
∫ 𝑙𝑛|1 + 𝑢3| + 𝑐
𝑦 =
1
3
𝑙𝑛|1 + 𝑢3| + 𝑐
𝑦 =
1
3
𝑙𝑛|1 + 𝑒3𝑥| + 𝑐
∫( 𝑎2
+ 𝑏2
𝑥2)
1
2 𝑑𝑥
∫( 𝑎2
+ 𝑏2
𝑥2)
1
2 𝑑𝑥
𝑢 = 𝑎2
+ 𝑏2
𝑥2
𝑑𝑢 = 2𝑏2
𝑥𝑑𝑥
𝑑𝑢
2𝑏2 𝑥
= 𝑑𝑥
∫( 𝑎2
+ 𝑏2
𝑥2)
1
2 𝑑𝑥
- 19. ∫( 𝑢)
1
2
𝑑𝑢
2𝑏2 𝑥
1
2𝑏2 ∫( 𝑢)
1
2 𝑑𝑢
1
2𝑏2 ∫
( 𝑢)
1
2
+1
1
2
+1
𝑑𝑢
1
2𝑏2 ∫
( 𝑢)
3
2
3
2
𝑑𝑢
1
2𝑏2 ∫
2( 𝑢)
3
2
3
+ 𝑐
𝑦 =
1
2𝑏2 ∗
2
3
( 𝑢)
3
2 + 𝑐
𝑦 =
1
3𝑏2
( 𝑢)
3
2 + 𝑐
𝑦 =
1
3𝑏2
( 𝑎2
+ 𝑏2
𝑥2)
3
2 + 𝑐
∫
3𝑎𝑥 𝑑𝑥
𝑏2+𝑐2 𝑥2
𝑢 = 𝑏2
+ 𝑐2
𝑥2
𝑑𝑢 = 2𝑥𝑐2
𝑑𝑥
𝑑𝑢
2𝑥𝑐2
= 𝑑𝑥
∫
3𝑎𝑥
𝑢
∗
𝑑𝑢
2𝑥𝑐2
∫
3𝑎
𝑢
∗
𝑑𝑢
2𝑐2
∫
3𝑎
2𝑐2
∗
1
𝑢
𝑑𝑢
3𝑎
2𝑐2
∫ 𝑙𝑛| 𝑢| + 𝑐
𝑦 =
3𝑎
2𝑐2 𝑙𝑛| 𝑢| + 𝑐 𝑦 =
3𝑎
2𝑐2 𝑙𝑛| 𝑏2
+ 𝑐2
𝑥2| + 𝑐
𝑦 = 𝑥
𝑑𝑦
𝑑𝑥
= 𝑥
𝑑𝑦
𝑑𝑥
= 1
- 20. ∫
𝑥3
𝑥 + 1
𝑑𝑥
PARA RESOLVER DEBEMOS APLICAR LA DIVISIÓN POR EL MÉTODO DE
RUFINI
𝑥2
− 𝑥 + 1 −
1
𝑥 + 1
∫ ( 𝑥2
− 𝑥 + 1 −
1
𝑥 + 1
) 𝑑𝑥
∫ 𝑥2
𝑑𝑥 − ∫ 𝑥 𝑑𝑥 + ∫ 𝑑𝑥 − ∫
1
𝑥 + 1
𝑑𝑥
∫
𝑥2+1
2 + 1
𝑑𝑥 − ∫
𝑥1+1
1 + 1
𝑑𝑥 + ∫
𝑥0+1
0 + 1
𝑑𝑥 − ∫ 𝑙𝑛| 𝑥 + 1| 𝑑𝑥
∫
𝑥3
3
+ 𝑐 − ∫
𝑥2
2
+ 𝑐 + ∫
𝑥
1
+ 𝑐 − ∫ 𝑙𝑛| 𝑥 + 1| + 𝑐
∫
1
3
𝑥3
+ 𝑐 − ∫
1
2
𝑥2
+ 𝑐 + ∫ 𝑥 + 𝑐 − ∫ 𝑙𝑛| 𝑥 + 1| + 𝑐
𝑦 =
1
3
𝑥3
−
1
2
𝑥2
+ 𝑥 − 𝑙𝑛| 𝑥 + 1| + 𝑐
∫
4𝑒3𝑥
1 + 𝑒 𝑥
𝑑𝑥
4 ∫
𝑒3𝑥
1 + 𝑒2𝑥
𝑑𝑥
𝑢 = 𝑒 𝑥
𝑑𝑢 = 𝑒 𝑥
𝑑𝑥
𝑑𝑢
𝑒 𝑥 = 𝑑𝑥 𝑑𝑢
𝑢
= 𝑑𝑥
4 ∫
𝑢3
1 + 𝑢2
∗
𝑑𝑢
𝑢
4 ∫
𝑢2
1 + 𝑢2
𝑑𝑢
- 21. PARA RESOLVER DEBEMOS APLICAR LA DIVISIÓN POR EL MÉTODO DE
RUFINI
1 −
1
1 + 𝑢2
4 ∫ (1 −
1
1 + 𝑢2
) 𝑑𝑢
4 (∫ 𝑑𝑢 − ∫
1
1 + 𝑢2
𝑑𝑢)
4 (∫
𝑢0+1
0 + 1
𝑑𝑢 − ∫
1
1 + 𝑢2
𝑑𝑢)
4 (∫
𝑢
1
+ 𝑐 − ∫ 𝑎𝑟𝑐 𝑡𝑔𝑢 + 𝑐)
𝑦 = 4( 𝑢 − 𝑎𝑟𝑐 𝑡𝑔𝑢) + 𝑐
𝑦 = 4𝑢 − 4𝑎𝑟𝑐 𝑡𝑔𝑢 + 𝑐
∫
2𝑥 − 1
2𝑥 + 3
𝑑𝑥
PARA RESOLVER DEBEMOS APLICAR LA DIVISIÓN POR EL MÉTODO DE
RUFINI
1 −
4
2𝑥 + 3
∫ (1 −
4
2𝑥 + 3
) 𝑑𝑥
∫ 𝑑𝑥 − ∫
4
2𝑥 + 3
𝑑𝑥
∫
𝑥0+1
0 + 1
𝑑𝑥 − 4 ∫
1
2𝑥 + 3
𝑑𝑥
∫
𝑥
1
+ 𝑐 − 4 ∫ 𝑙𝑛|2𝑥 + 3| + 𝑐
- 22. 𝑦 = 𝑥 − 4𝑙𝑛|2𝑥 + 3| + 𝑐