Giraph Travelling Salesman Example
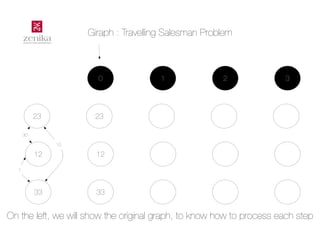
- 1. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 24 24 30 10 12 12 32 32 1 33 33 31 31 On the left, we will show the original graph, to know how to process each step
- 2. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 24 24 30 10 12 12 32 32 1 33 33 31 31 Superstep 0 begins
- 3. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 24 24 30 10 12 12 32 32 1 33 33 31 31 Superstep 0 : we compute vertex n°1, nothing to do, it is not the source
- 4. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 24 24 30 10 12 12 32 32 1 33 33 31 31 Superstep 0 : we compute vertex n°2, the source
- 5. Giraph : Travelling Salesman Problem Superstep : 0 1 2 3 23 23 24 24 30 2,12+30 10 12 12 32 32 1 2,12+1 33 33 31 31 The source sends all the possible paths and their values to the others nodes
- 6. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 24 24 30 2,12+30 10 12 12 32 32 1 2,12+1 33 33 31 31 The source then votes to halt
- 7. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 24 24 30 2,12+30 10 12 12 32 32 1 2,12+1 33 33 31 31 Superstep 0 : we compute vertex n°3, nothing happens as it is not the source
- 8. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 24 24 30 2,12+30 10 12 12 12 32 32 1 2,12+1 33 33 33 31 31 Superstep 1 begins
- 9. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 24 24 30 2,12+30 10 12 12 12 32 32 1 2,12+1 33 33 33 31 31 Superstep 1 : we compute vertex n°1
- 10. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 24 24 30 2,12+30 10 12 12 12 32 32 1 2,12+1 21,42+10+23 33 33 33 31 31 Superstep 1 : we compute vertex n°1
- 11. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 24 24 30 2,12+30 10 12 12 12 32 32 1 2,12+1 21,42+10+23 33 33 33 31 31 Superstep 1 : we compute vertex n°3
- 12. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 24 24 30 2,12+30 23,13+10+33 10 12 12 12 32 32 1 2,12+1 21,42+10+23 33 33 33 31 31 Superstep 1 : we compute vertex n°3
- 13. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 24 30 2,12+30 23,13+10+33 10 12 12 12 12 32 1 2,12+1 21,42+10+23 33 33 33 33 31 Superstep 2 begins
- 14. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 24 30 2,12+30 23,13+10+33 10 12 12 12 12 32 1 2,12+1 21,42+10+23 33 33 33 33 31 Superstep 2 : we compute vertex n°1
- 15. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 24 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 32 1 2,12+1 21,42+10+23 33 33 33 33 31 Superstep 2 : we compute vertex n°1
- 16. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 24 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 32 1 2,12+1 21,42+10+23 33 33 33 33 31 Superstep 2 : we compute vertex n°3
- 17. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 24 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 32 1 2,12+1 21,42+10+23 213,75+10+33=118 33 33 33 33 31 Superstep 2 : we compute vertex n°3
- 18. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 23 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 12 1 2,12+1 21,42+10+23 213,75+10+33=118 33 33 33 33 33 Superstep 3 begins
- 19. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 23 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 12 1 2,12+1 21,42+10+23 213,75+10+33=118 33 33 33 33 33 Superstep 3 : we compute vertex n°1
- 20. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 23 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 12 1 2,12+1 21,42+10+23 213,75+10+33=118 33 33 33 33 33 Superstep 3 : we compute vertex n°1 : votes to Halt
- 21. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 23 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 12 1 2,12+1 21,42+10+23 213,75+10+33=118 33 33 33 33 33 Superstep 3 : we compute the source, reactivated by the messages received
- 22. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 23 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 12 1 2,12+1 21,42+10+23 213,75+10+33=118 33 33 33 33 33 The source compares the values received and finds the minimum distance
- 23. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 23 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 109 1 2,12+1 21,42+10+23 213,75+10+33=118 33 33 33 33 33 and sets its value as the minimum
- 24. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 23 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 109 1 2,12+1 21,42+10+23 213,75+10+33=118 33 33 33 33 33 The source then votes to Halt
- 25. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 23 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 109 1 2,12+1 21,42+10+23 213,75+10+33=118 33 33 33 33 33 Superstep 3 : we compute vertex n°3
- 26. Giraph : Travelling Salesman Problem 0 1 2 3 23 23 23 23 23 30 2,12+30 23,13+10+33 231,56+30+23=109 10 12 12 12 12 109 1 2,12+1 21,42+10+23 213,75+10+33=118 33 33 33 33 33 Superstep 3 : we compute vertex n°3 : votes to Halt, ends the process