More Related Content
PDF
PDF
PDF
PDF
Asymptotically optimal policies in multiarmed bandit problems PDF
PDF
PDF
PPTX
Scaling up Machine Learning Algorithms for Classification Similar to Multi-state extension of asymmetric simple exclusion process
PPTX
【招待講演】パラメータ制約付き行列分解のベイズ汎化誤差解析【StatsML若手シンポ2020】 PDF
渡辺澄夫著「ベイズ統計の理論と方法」5.1 マルコフ連鎖モンテカルロ法 PDF
PDF
el text.life science6.tsuneda191106 PDF
El text.life science6.tsuneda191106 PDF
PDF
PDF
PDF
PDF
PDF
密度汎関数法 Density Functional Theory (DFT)の基礎第6回 PDF
PDF
PRML輪講用資料10章(パターン認識と機械学習,近似推論法) Recently uploaded
PPTX
Introduction to Japanese Language Learning.pptx PDF
プログラミング講座 【小学校高学年向け】Revision 6 2025/11/30 PDF
ふみこんで学ぶ世界遺産700<第2版>世界遺産検定準1級公式テキスト(2026年発売) PDF
高等専門学校卒業資格における準学士学位 (Associate Degre) の制度的展望 —国際的学位制度との比較から— PDF
横浜国立大学3年生に向けて研究室を紹介する資料【2026年度研究室配属について】 PDF
横浜国立大学3年生に向けて研究室を紹介するスライド【2026年度研究室配属について】 Multi-state extension of asymmetric simple exclusion process
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
非対称単純排他過程 (ASEP)
• 体積排他相互作用をもつマルコフ過程.
ratep1で右へホッピング.
rate p2で左へホッピング.
隣に粒子がいる場合,移動不可.
• 交通流やmRNAの転写モデルとしてよく知られる.
• 密度プロファイルに相転移がある.
(左から)
低密度相,カレント最大相,
共存相,高密度相
[Sasamoto 03]
• Uq(sl2)不変(閉じた境界条件の場合).一般の境界条件下では
Askey-Wilson代数が現れる.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
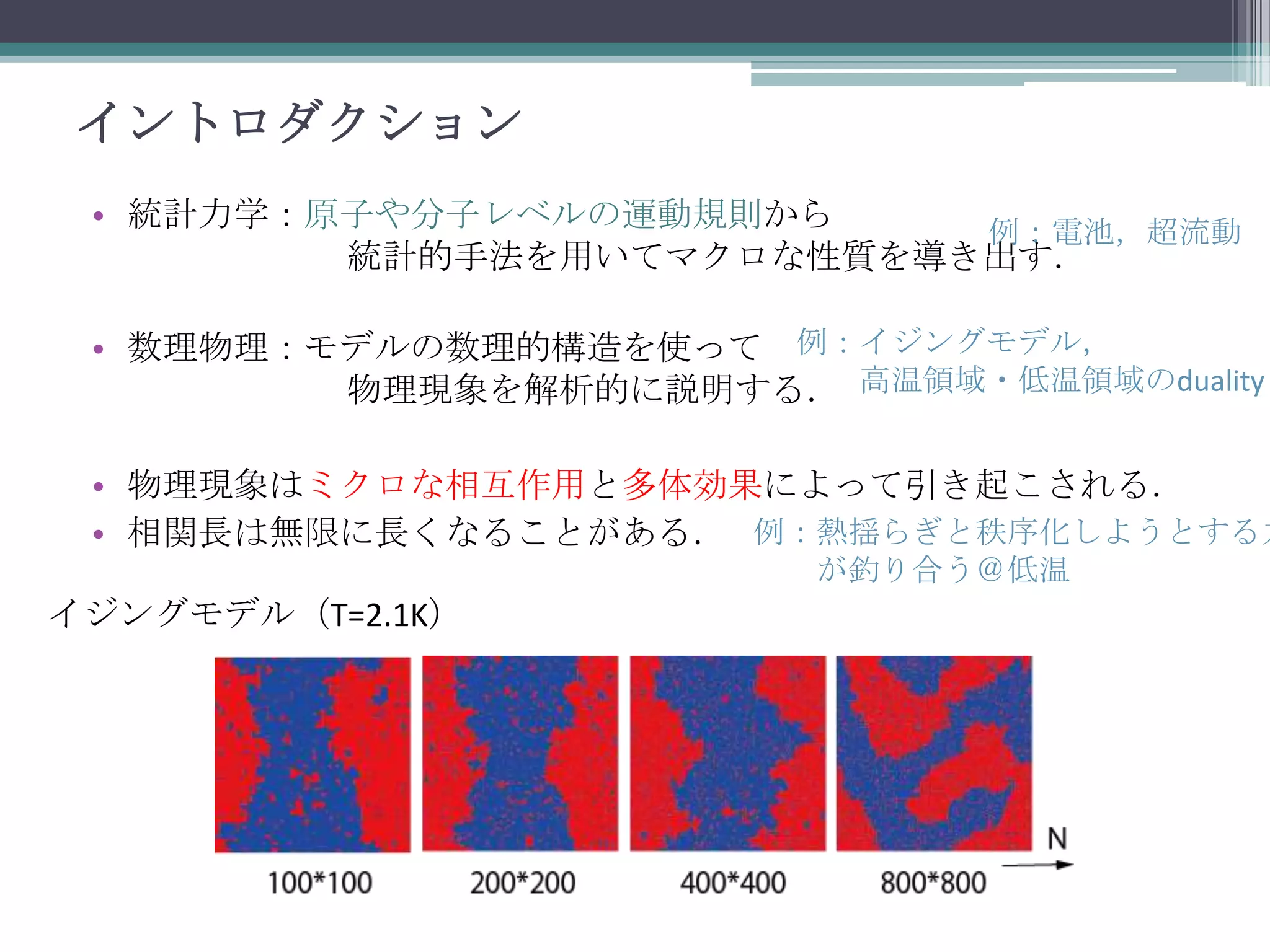
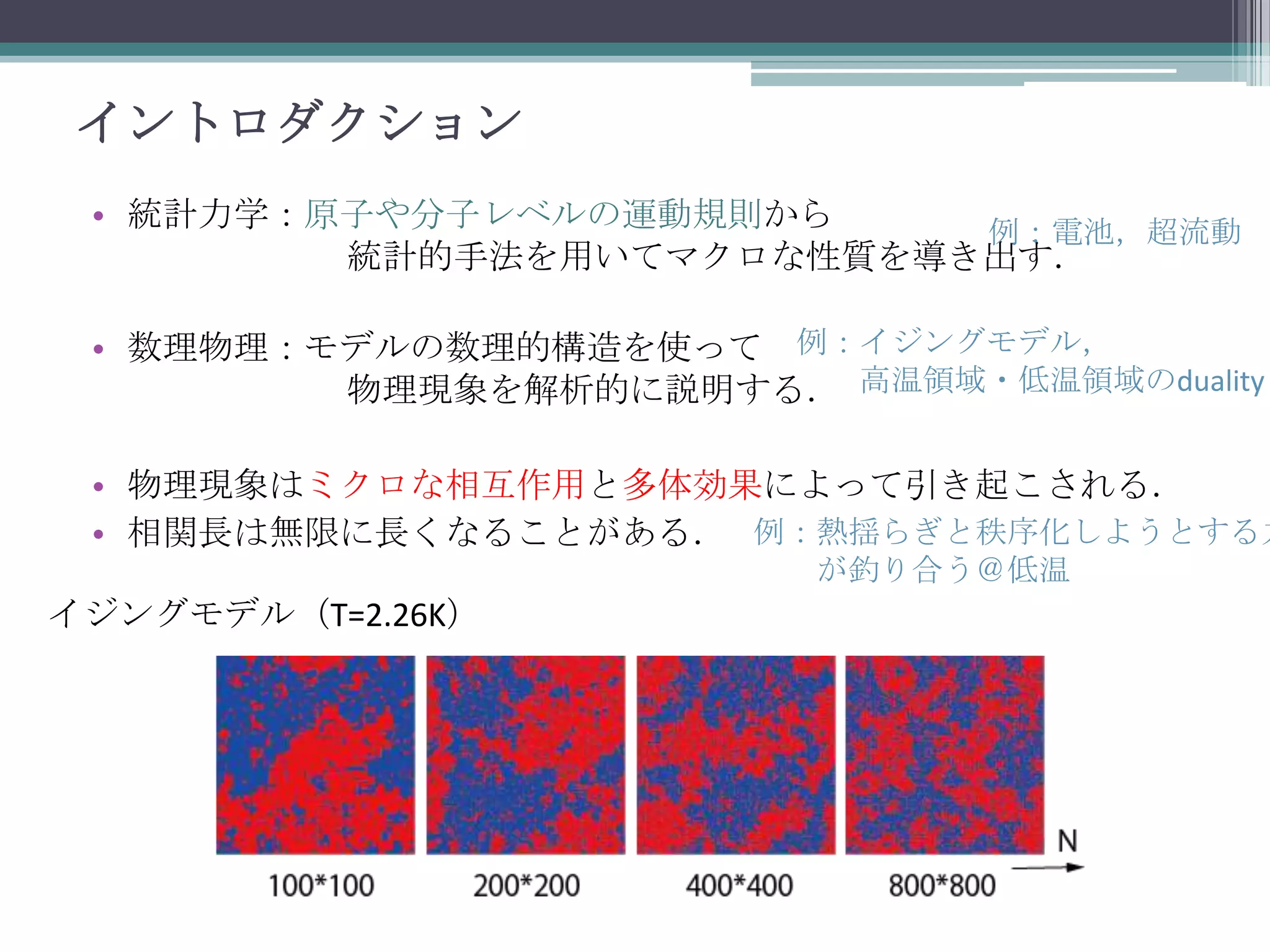
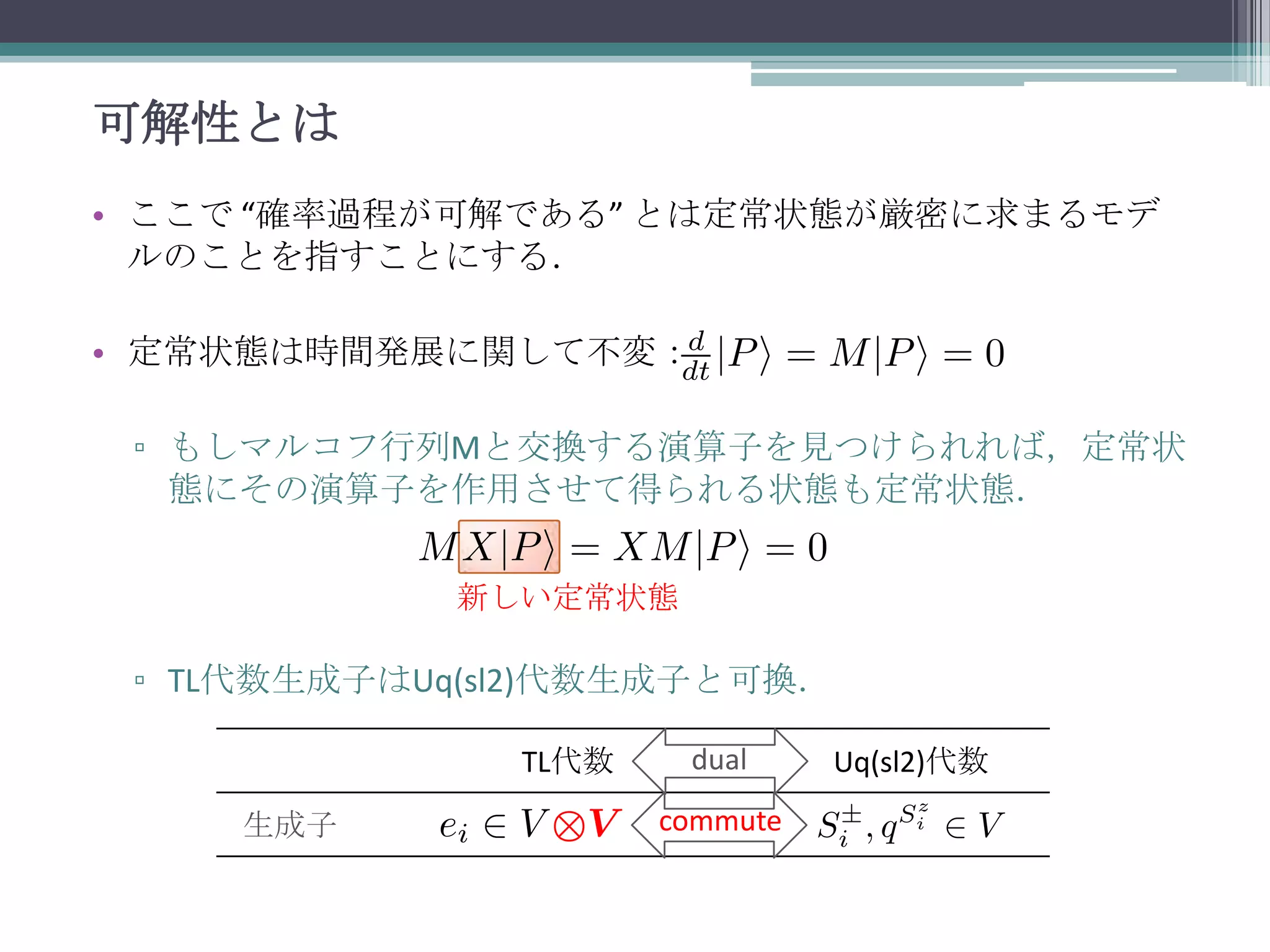
可解性とは
• ここで “確率過程が可解である”とは定常状態が厳密に求まるモデ
ルのことを指すことにする.
• 定常状態は時間発展に関して不変:
▫ もしマルコフ行列Mと交換する演算子を見つけられれば,定常状
態にその演算子を作用させて得られる状態も定常状態.
新しい定常状態
▫ TL代数生成子はUq(sl2)代数生成子と可換.
TL代数
生成子
dual
commute
Uq(sl2)代数
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.

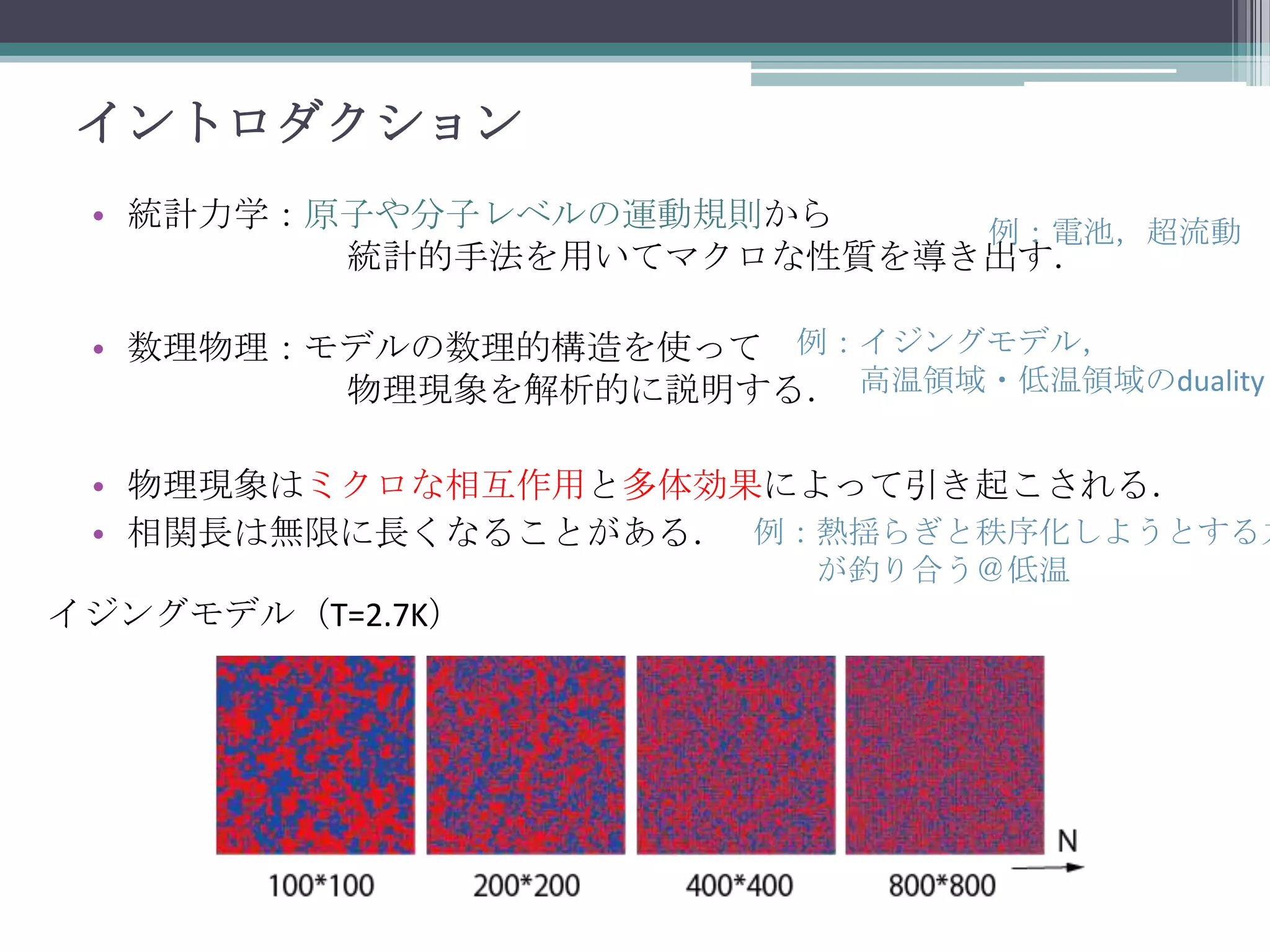

![非対称単純排他過程 (ASEP)
• 体積排他相互作用をもつマルコフ過程.
rate p1で右へホッピング.
rate p2で左へホッピング.
隣に粒子がいる場合,移動不可.
• 交通流やmRNAの転写モデルとしてよく知られる.
• 密度プロファイルに相転移がある.
(左から)
低密度相,カレント最大相,
共存相,高密度相
[Sasamoto 03]
• Uq(sl2)不変(閉じた境界条件の場合).一般の境界条件下では
Askey-Wilson代数が現れる.](https://image.slidesharecdn.com/jokyo21012014def-140201214528-phpapp01/75/Multi-state-extension-of-asymmetric-simple-exclusion-process-6-2048.jpg)



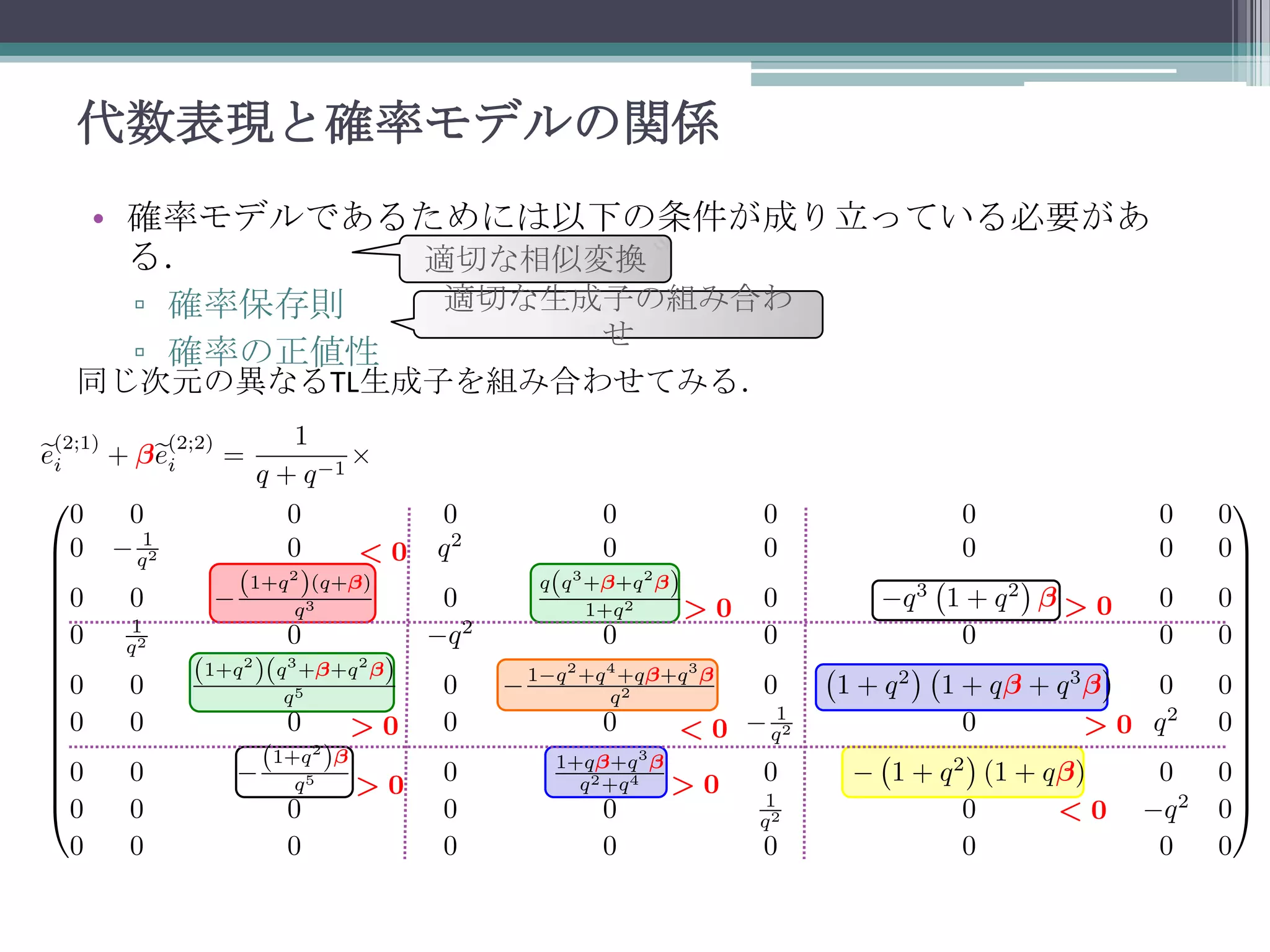
![代数表現と確率モデルの関係
• 元々のTL生成子に対してはgraphicalな表現が与えられている.
i
i
i
i+1
i+1
i
i+1
i+1
• テンソル積から空間の入れ替えに関して対称な部分空間を取り出し
て高次元表現を構成.
例:3状態の場合
1/2
1/2
1
0
射影演算子Yで
消える部分空間
i
Y
i+1
Y
i
Y
i+1
Y
Y
i
Y
i+1
Y
i
Y
i+1
[Zinn-Justin 07]](https://image.slidesharecdn.com/jokyo21012014def-140201214528-phpapp01/75/Multi-state-extension-of-asymmetric-simple-exclusion-process-10-2048.jpg)







![可解性とは—粒子密度—
• 導かれた公式:(ℓ+1)状態の粒子密度の計算は2状態の密度計算に分
解される.
• 2状態の場合の表式 [Sandow-Schutz 94]
large Nでの漸近形
高密度相から0密度相への減衰速度は
系の状態数に依存する.](https://image.slidesharecdn.com/jokyo21012014def-140201214528-phpapp01/75/Multi-state-extension-of-asymmetric-simple-exclusion-process-24-2048.jpg)