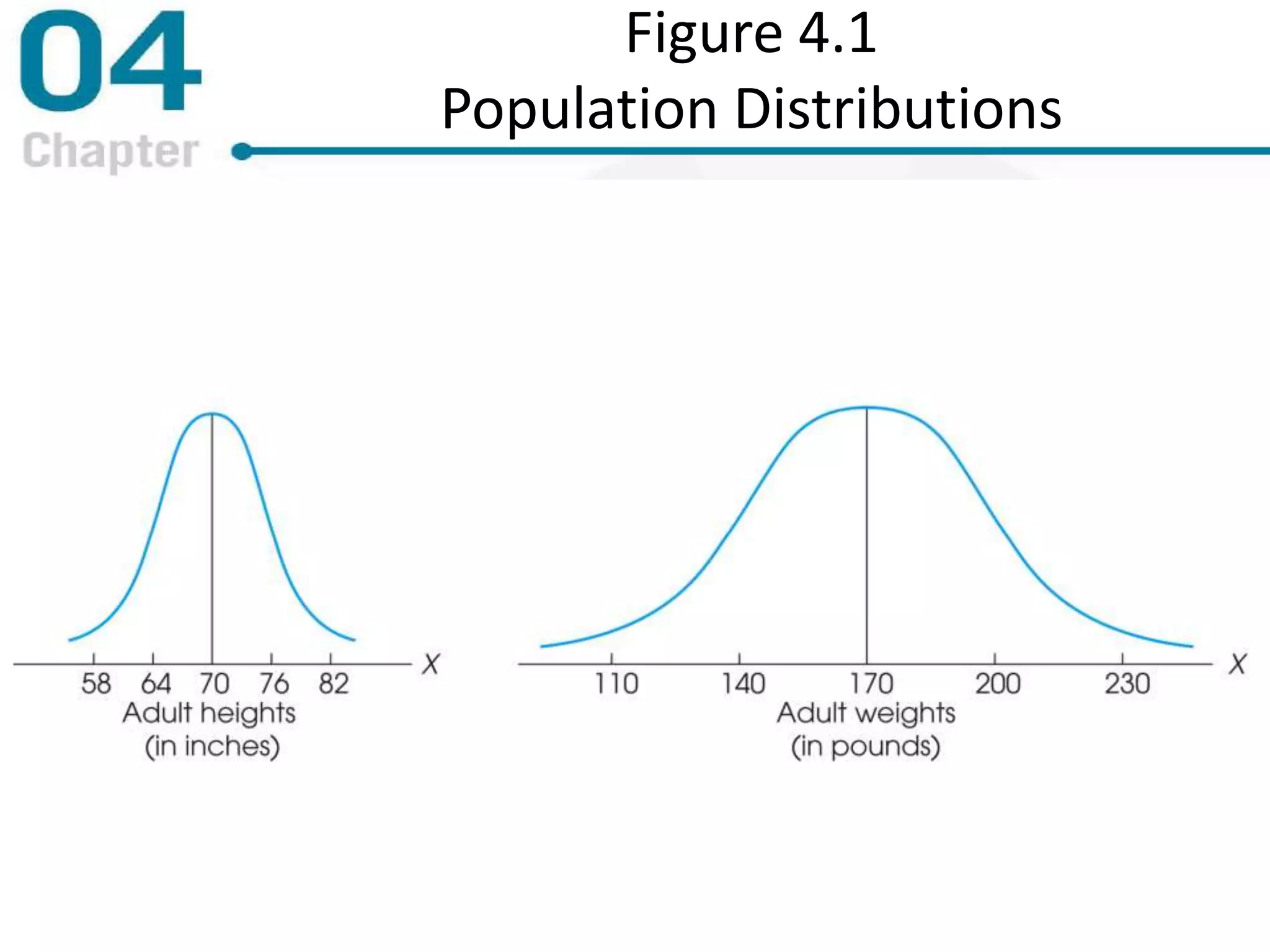
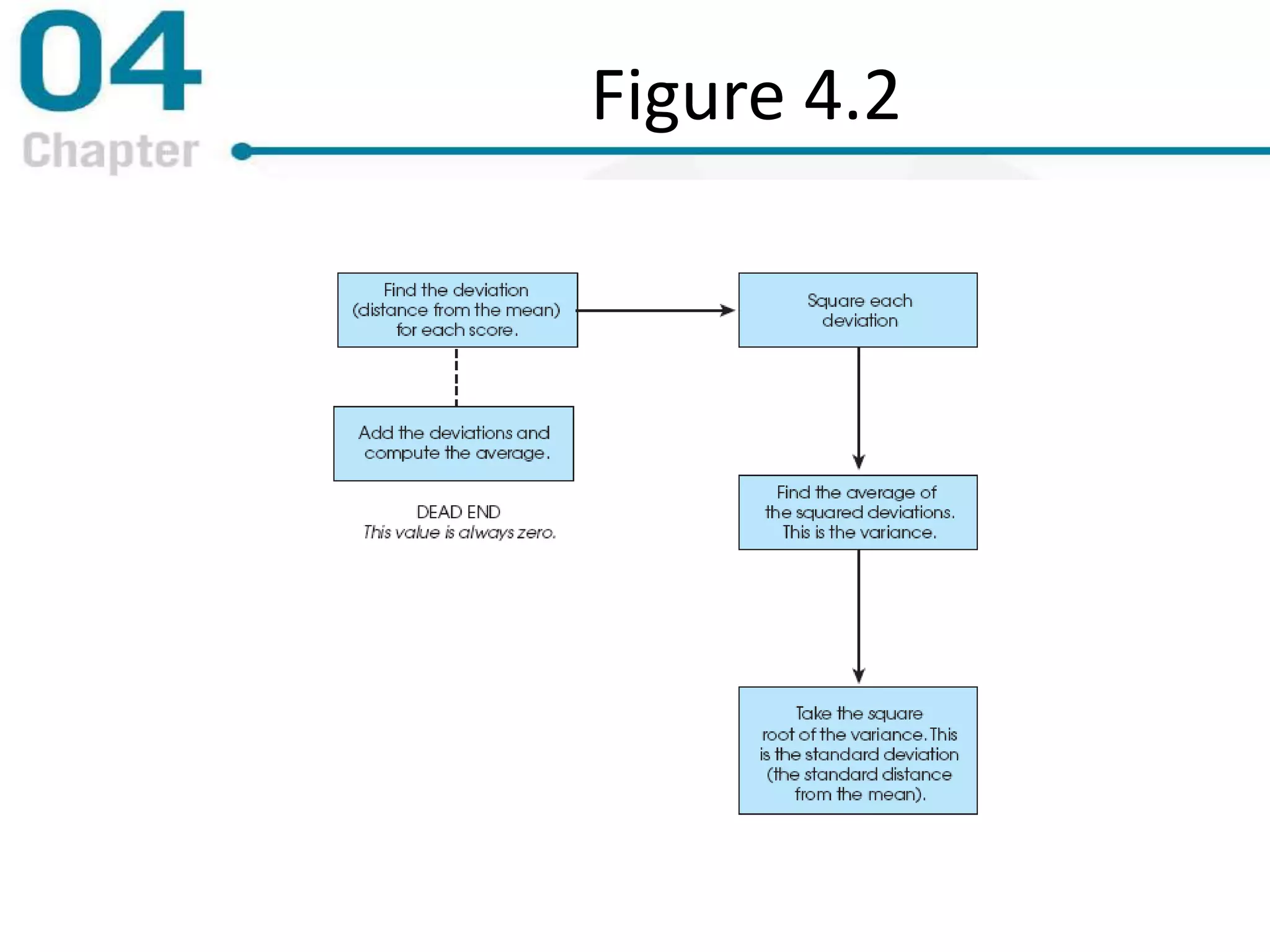
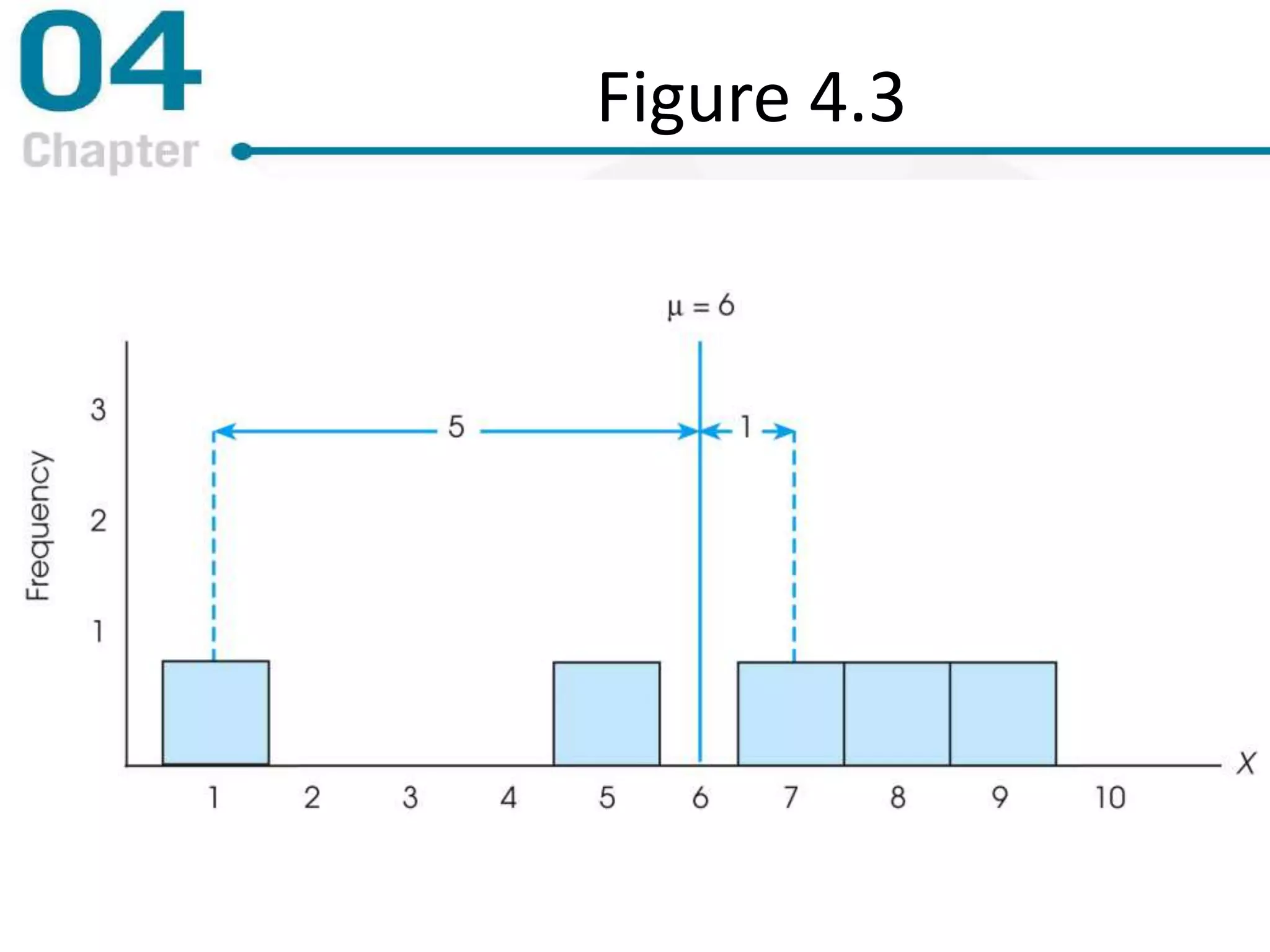
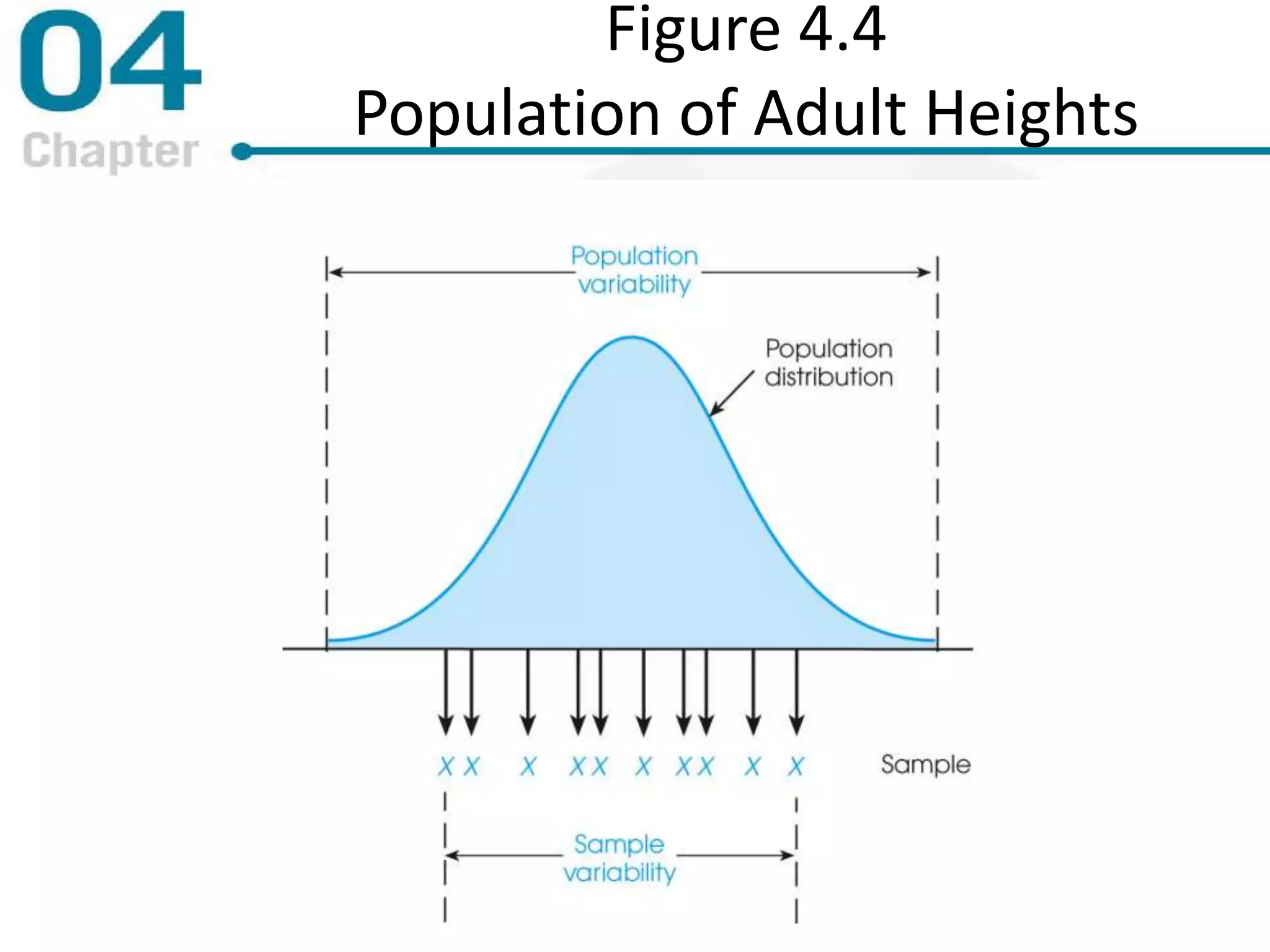
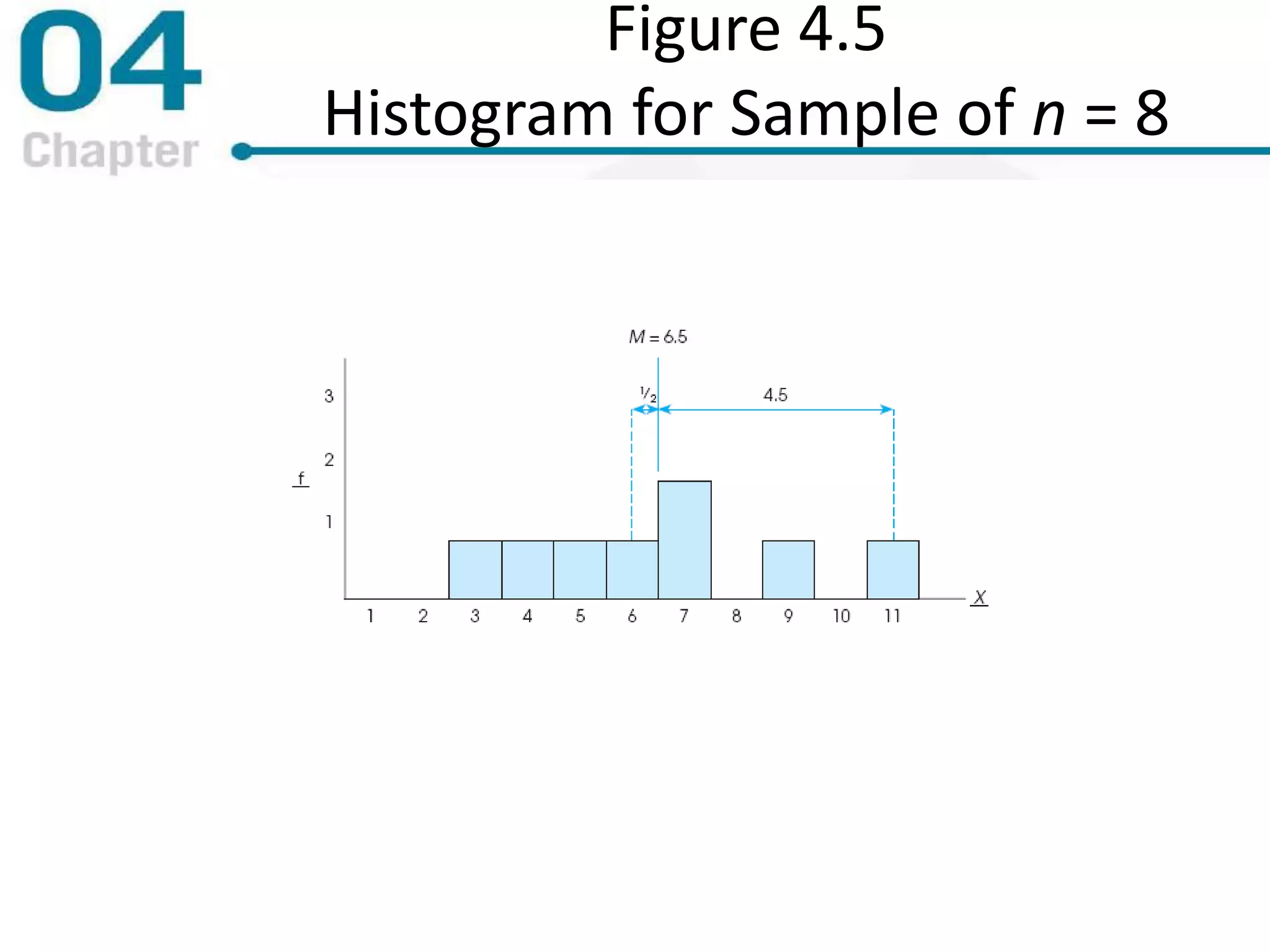
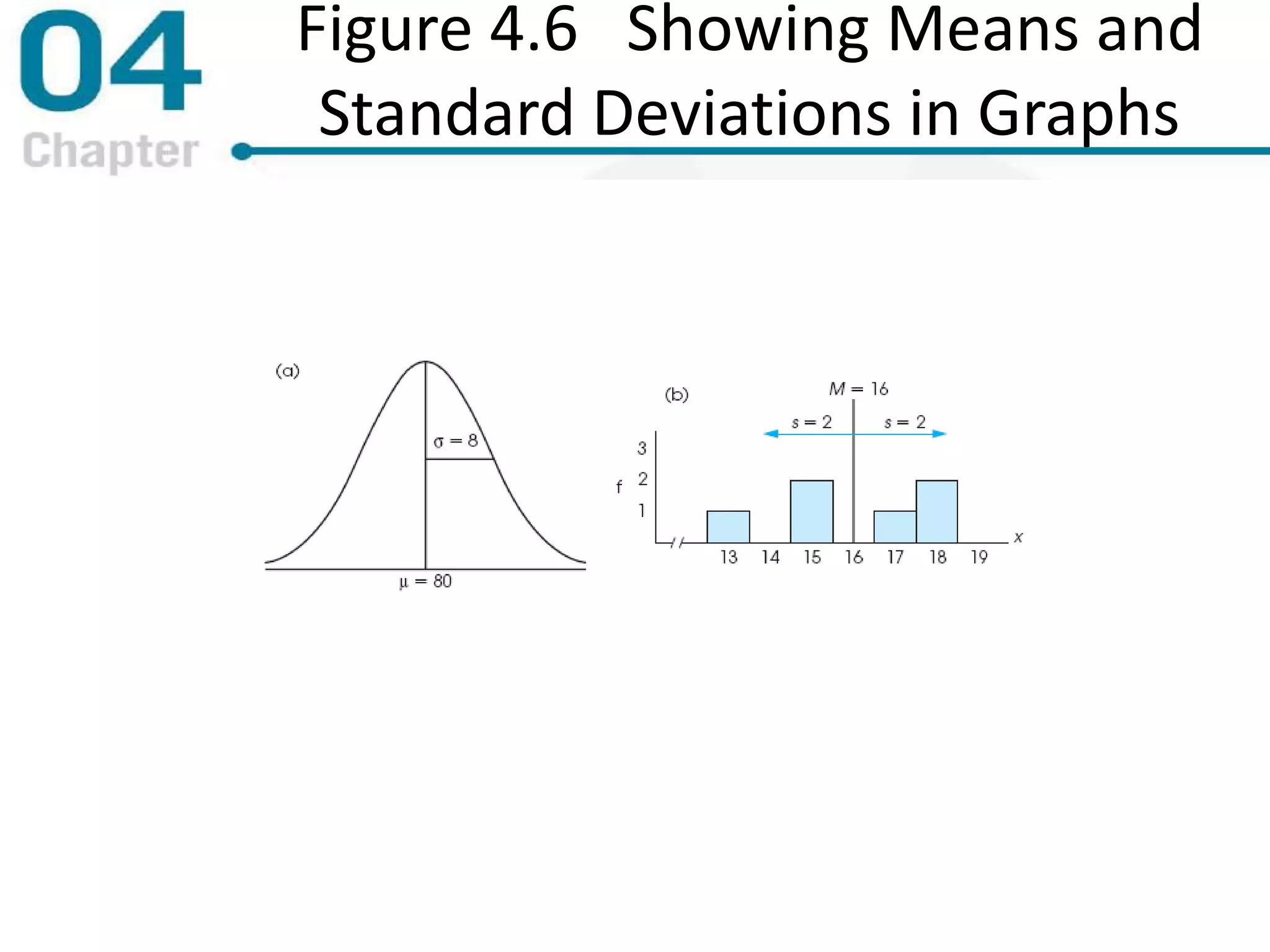
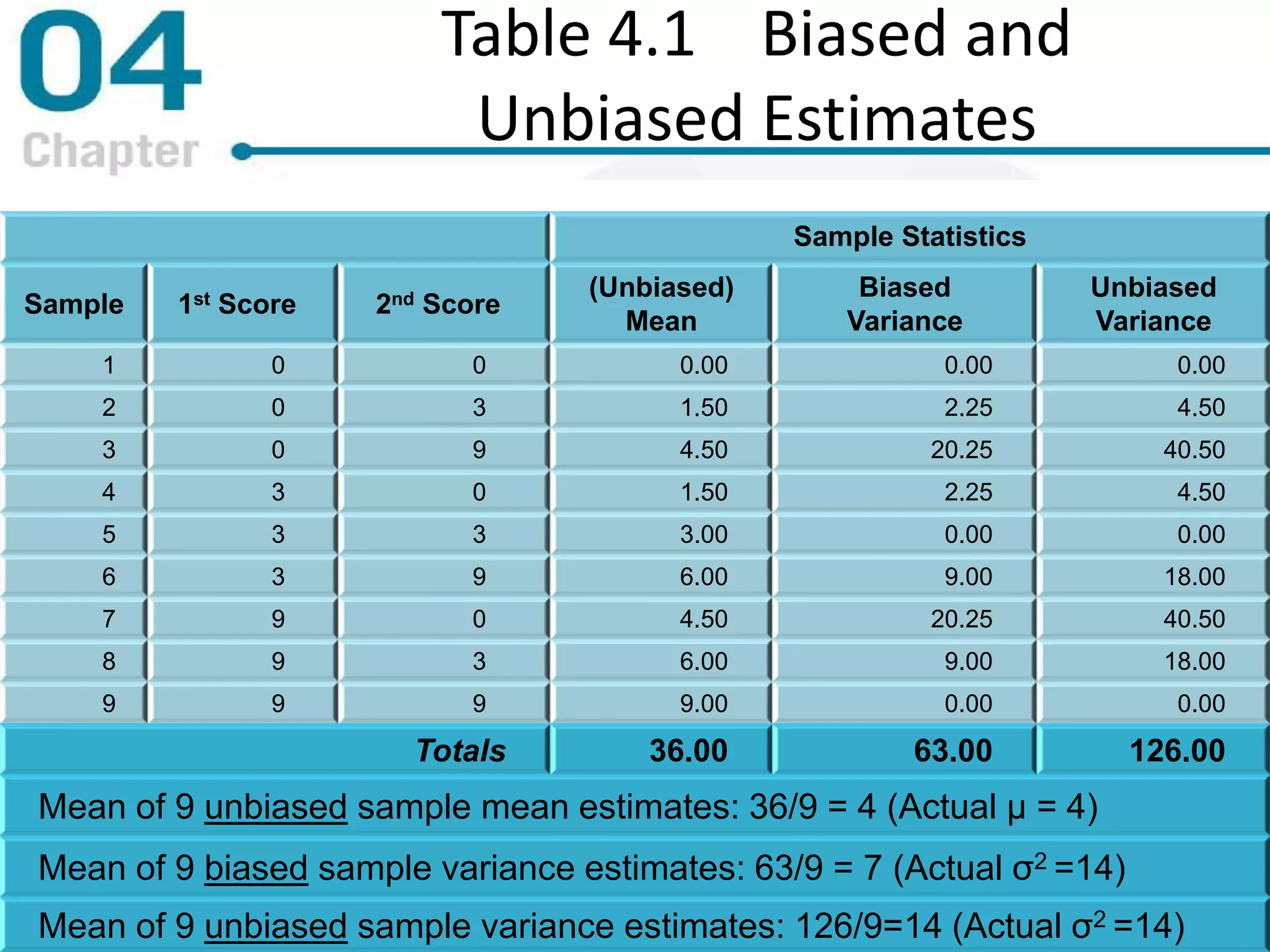
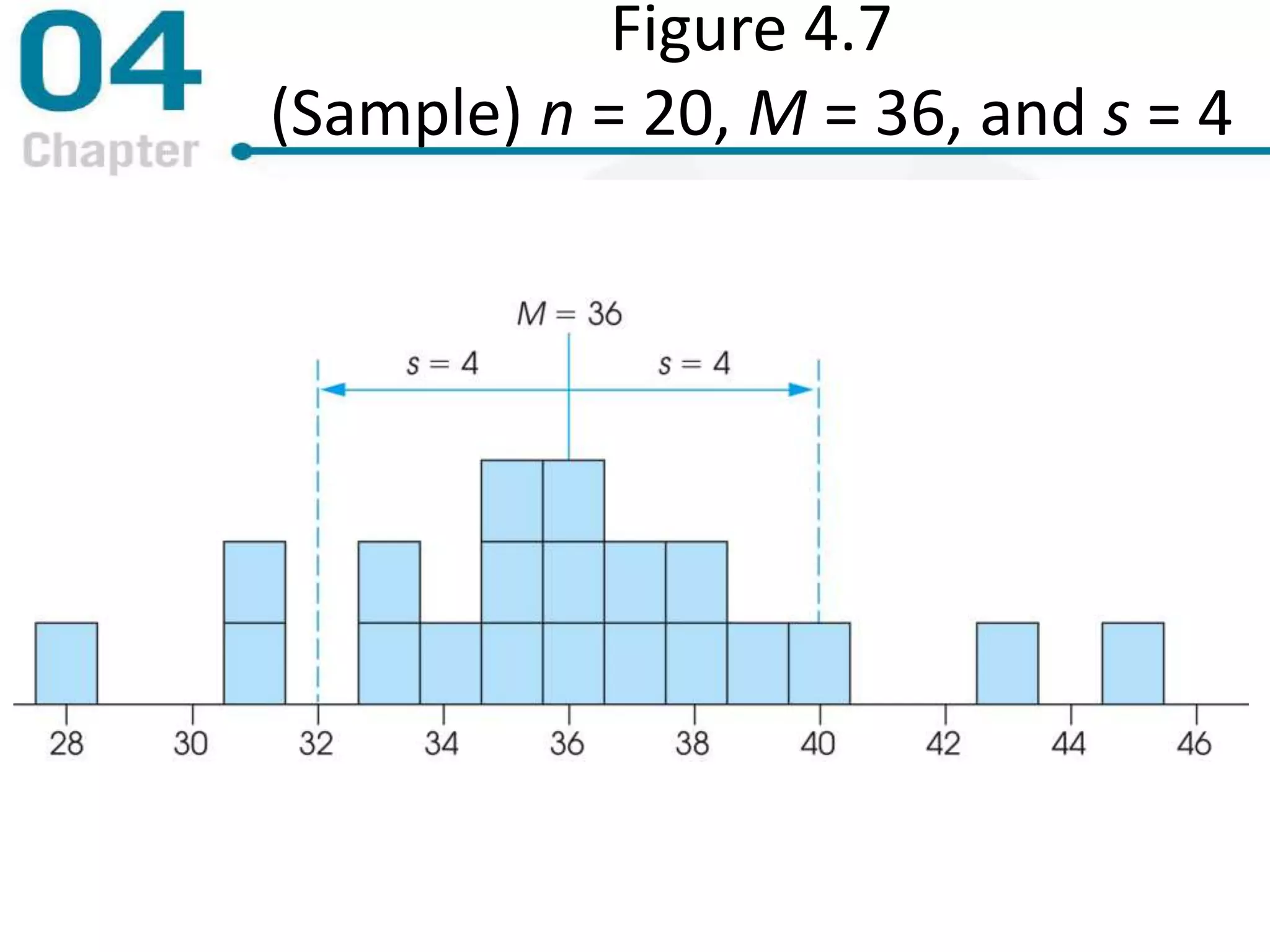
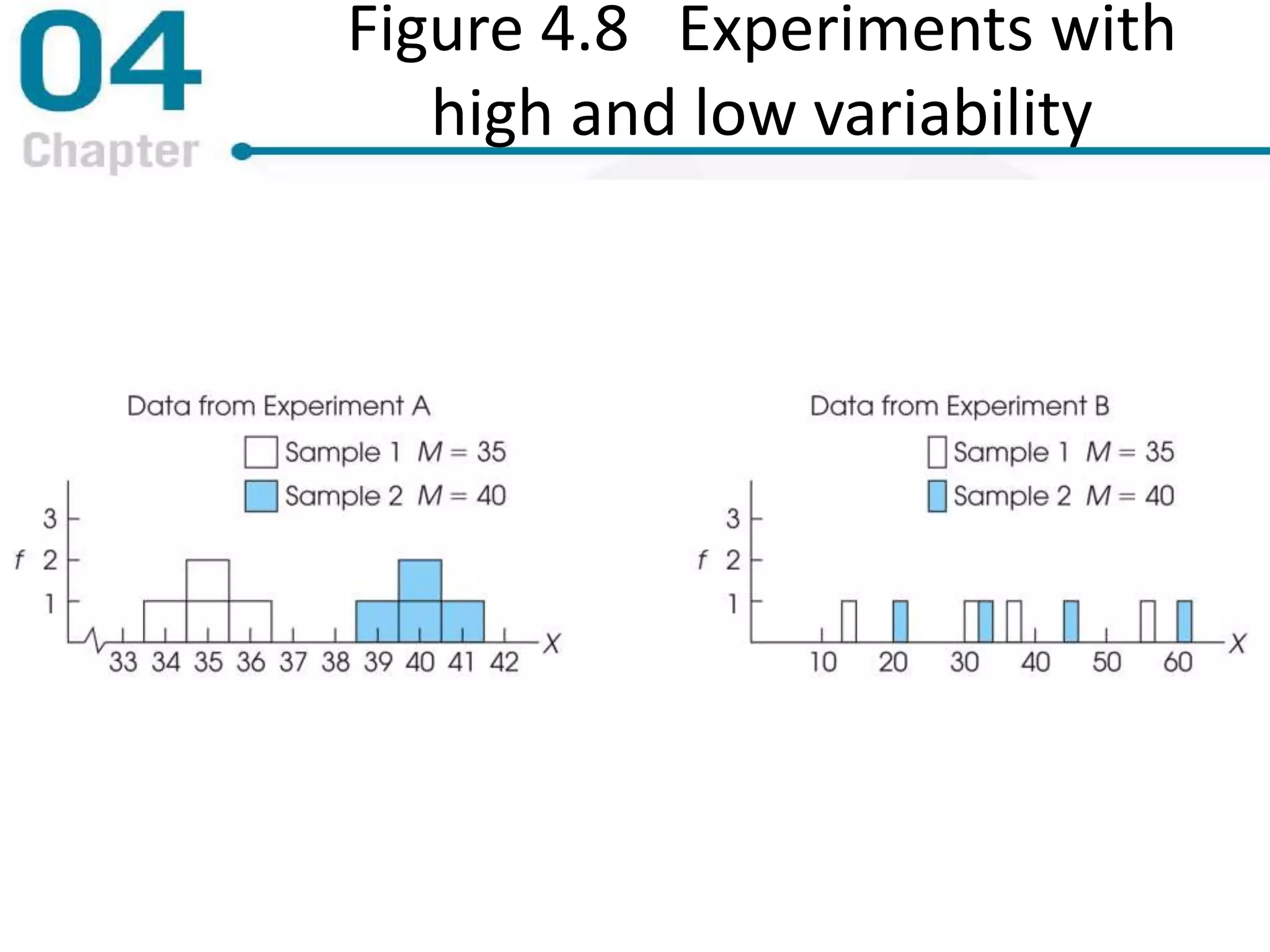
Chapter 4 focuses on measures of variability, specifically range, variance, and standard deviation, explaining their importance in statistical analysis. It details methods for calculating these measures for both populations and samples, highlighting the differences and implications of biased versus unbiased statistics. Additionally, the chapter discusses the relevance of variability in interpreting data distributions and making inferences about populations.