Designed for OCR A Level mathematics.

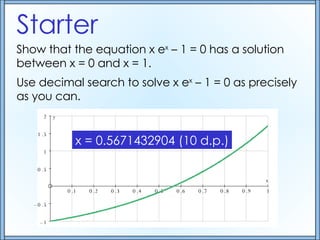
1. Starter Show that the equation x e x – 1 = 0 has a solution between x = 0 and x = 1. Use decimal search to solve x e x – 1 = 0 as precisely as you can. x = 0.5671432904 (10 d.p.)

2. Objective: to use iteration to produce a sequence that converges to a root

3. Iteration The equation x e x – 1 = 0 can be rearranged as follows:

4. Iteration The equation x e x – 1 = 0 can be rearranged as follows: This can be turned into an iterative formula:

5. Iteration The equation x e x – 1 = 0 can be rearranged as follows: This can be turned into an iterative formula:

6. Iteration Assume x 0 = 0. Complete this table: x 21 x 10 x 20 x 9 x 19 x 8 x 18 x 7 x 17 x 6 x 16 x 5 x 15 x 4 x 14 x 3 x 13 x 2 x 12 x 1 x 11 0 x 0

7. Iteration Assume x 0 = 0. Complete this table: x 21 x 10 x 20 x 9 x 19 x 8 x 18 x 7 x 17 x 6 x 16 x 5 x 15 x 4 x 14 x 3 x 13 x 2 x 12 1 x 1 x 11 0 x 0

8. Iteration Assume x 0 = 0. Complete this table: x 21 x 10 x 20 x 9 x 19 x 8 x 18 x 7 x 17 x 6 x 16 x 5 x 15 x 4 x 14 x 3 x 13 0.3678794412 x 2 x 12 1 x 1 x 11 0 x 0

9. Iteration Assume x 0 = 0. Complete this table: x 21 x 10 x 20 x 9 x 19 x 8 x 18 x 7 x 17 x 6 x 16 x 5 x 15 x 4 x 14 0.6922006276 x 3 x 13 0.3678794412 x 2 x 12 1 x 1 x 11 0 x 0

10. Iteration Assume x 0 = 0. Complete this table: x 21 x 10 x 20 x 9 x 19 x 8 x 18 x 7 x 17 x 6 x 16 x 5 x 15 0.5004735006 x 4 x 14 0.6922006276 x 3 x 13 0.3678794412 x 2 x 12 1 x 1 x 11 0 x 0

11. Iteration Assume x 0 = 0. Complete this table: x 21 x 10 x 20 x 9 x 19 x 8 x 18 x 7 x 17 x 6 x 16 0.6062435351 x 5 x 15 0.5004735006 x 4 x 14 0.6922006276 x 3 x 13 0.3678794412 x 2 x 12 1 x 1 x 11 0 x 0

12. Iteration Assume x 0 = 0. Complete this table: x 21 x 10 x 20 x 9 x 19 x 8 x 18 x 7 x 17 0.545395786 x 6 x 16 0.6062435351 x 5 x 15 0.5004735006 x 4 x 14 0.6922006276 x 3 x 13 0.3678794412 x 2 x 12 1 x 1 x 11 0 x 0

13. Iteration Assume x 0 = 0. Complete this table: 0.5671477143 x 21 0.5648793474 x 10 0.5671354902 x 20 0.5711431151 x 9 0.567157044 x 19 0.5601154614 x 8 0.5671190401 x 18 0.5796123355 x 7 0.5671860501 x 17 0.545395786 x 6 0.5670678984 x 16 0.6062435351 x 5 0.5672762322 x 15 0.5004735006 x 4 0.5669089119 x 14 0.6922006276 x 3 0.5675566373 x 13 0.3678794412 x 2 0.5664147331 x 12 1 x 1 0.568428725 x 11 0 x 0

14. Question a) Show that a solution of the equation x 3 – 3x – 5 = 0 lies between 2 and 3. b) Show that the equation can be rearranged into the form c) Use iteration based on this rearrangement to find the solution accurate to five decimal places. d) Show the equation can also be rearranged into the form e) Show that iteration based on this rearrangement fails to converge to a solution.

15. Core 3 & 4 Textbook Page 143 Exercise 8B Questions 4, 5, 6 Homework Numerical Methods Worksheet C

16. Core 3 June 2006 Core 3 January 2007