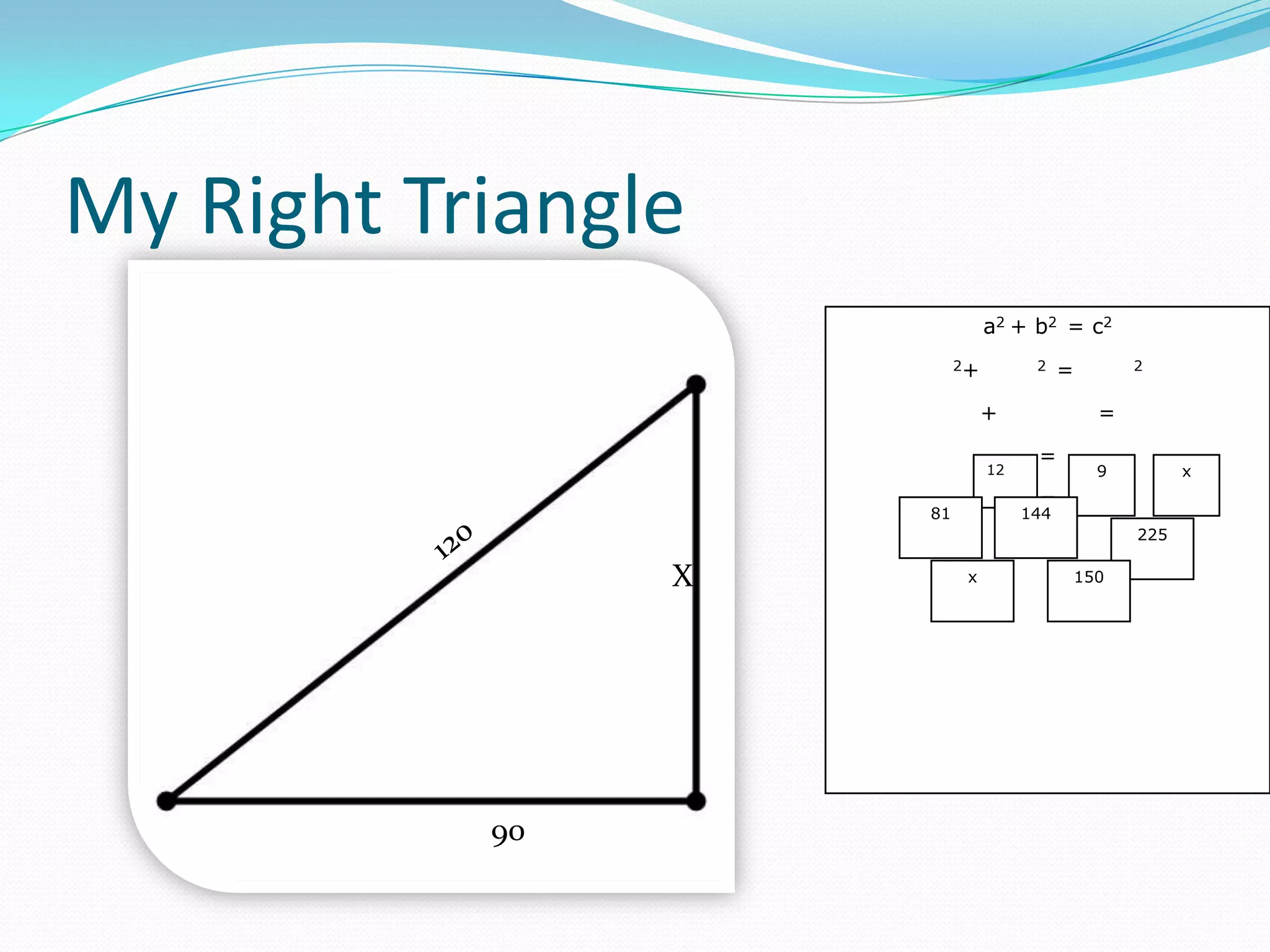
The Pythagorean theorem states that in any right triangle, the sum of the squares of the two shorter sides equals the square of the longest side. It is used for right triangles, which have one 90 degree angle. The distance formula calculates the distance between two points by taking the difference of the x-coordinates squared and the difference of the y-coordinates squared, adding those values, and taking the square root of the sum. An example is worked out step-by-step to demonstrate using the distance formula.

1. Pythagorean Theorem & Distance FormulaKwamaine Person

2. What Is Pythagorean Theorem ?Pythagoras' theorem states that in any right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.What Do the Variables stand for ?What type of triangle do we use the theorem for?The variables in the algebraic statement of the Theorem stand for the lengths of the sides of a right triangle.The right angled triangle has a right angle of 90° as one of its interior angles. In the image here the right angle is marked with the white square.

3. My Right Trianglea2 + b2 = c22+ 2 = 2 + === 129x81144225x150120X90

4. What is the distance formulaThe Formula a2+ b2= C2 d= square root of ((x2-x1)^2+(y2-y1)^21.Get the line that you are going to measure.A Find the coordinates of the line's endpoints.3Take the x-coordinates of both points and subtract them.4Square that amount.5Get the y-coordinates of both points and subtract them.6Square that amount.7Add both of the squares.8Find the square root of the final sum.9You have found the length of line, in units.

5. Distance Formula Example