Cartea lui Valeriu Lupu abordează algoritmii din perspectiva unui curs de programare, concentrându-se pe concepte fundamentale precum greedy, divide et impera, programare dinamică și backtracking, evidențiind aspectele esteticii algoritmilor. De asemenea, oferă o introducere în limbajul Visual Basic și analizează metodele de implementare a algoritmilor prin exemple intuitive, accesibile și fără o bază matematică avansată. Cu un conținut fluid, cartea se dovedește utilă atât pentru începători, cât și pentru cei cu experiență limitată în programare.

1. VALERIU LUPU
ALGORITMI. TEHNICI ŞI
LIMBAJE DE PROGRAMARE
EDITURA UNIVERSITĂŢII “ŞTEFAN cel MARE” SUCEAVA
2007
3

2. Prefaţă
Cartea isi propune in primul rand sa fie un curs si nu o "enciclopedie" de algoritmi. Pornind de la structurile de date
cele mai uzuale si de la analiza eficientei algoritmilor, cartea se concentreaza pe principiile fundamentale de elaborare a
algoritmilor: greedy, divide et impera, programare dinamica, backtracking. Majoritatea algoritmilor selectati au o conotatie
estetica. Efortul necesar pentru intelegerea elementelor mai subtile este uneori considerabil. Ce este insa un algoritm "estetic"?
Putem raspunde foarte simplu: un algoritm este estetic daca exprima mult in cuvinte putine. Un algoritm estetic este oare in
mod necesar si eficient? Cartea raspunde si acestor intrebari.
In al doilea rand, cartea prezinta mecanismele interne esentiale ale limbajului Visual Basic si trateaza implementarea
algoritmilor in mod iterative cat si recursiv. Totusi, aceasta carte nu este un curs complet de Visual Basic. Algoritmii nu sunt
pur si simplu "transcrisi" din pseudo-cod in limbajul Visual Basic, ci sunt reganditi din punct de vedere al programarii
orientate pe obiect. Speram ca, dupa citirea cartii, veti dezvolta aplicatii de programare in mod iterative cat si recursiv si veti
elabora implementari ale altor structuri de date. Programele pot fi scrise si in limbajul C#. Acest limbaj se caracterizeaza, in
principal, prin introducerea claselor parametrice si a unui mecanism de tratare a exceptiilor foarte avansat, facilitati deosebit de
importante pentru dezvoltarea de biblioteci C#.
Fara a face concesii rigorii matematice, prezentarea este intuitiva, cu numeroase exemple. Am evitat, pe cat posibil,
situatia in care o carte de informatica incepe - spre disperarea ne-matematicienilor - cu celebrul "Fie ... ", sau cu o definitie.
Am incercat, pe de alta parte, sa evitam situatia cand totul "este evident", sau "se poate demonstra". Fiecare capitol este
conceput fluid, ca o mica poveste, cu putine referinte si note. Multe rezultate mai tehnice sunt obtinute ca exercitii. Algoritmii
sunt prezentati intr-un limbaj pseudo-cod compact, fara detalii inutile.
Presupunem ca cititorul nu are la baza cel putin un curs introductiv in programare, fiindu-i straini termeni precum
algoritm, recursivitate, functie, procedura si pseudo-cod. Exista mai multe modalitati de parcurgere a cartii. In functie de
interesul si pregatirea cititorului, acesta poate alege oricare din partile referitoare la elaborarea, analiza, sau implementarea
algoritmilor. Cu exceptia partilor de analiza a eficientei algoritmilor (unde sunt necesare elemente de matematici superioare),
cartea poate fi parcursa si de catre un elev de liceu. Pentru parcurgerea sectiunilor de implementare, este recomandabila
cunoasterea limbajului Visual Basic.
S-a dovedit utila si experienta autorului de peste douzeci de ani in dezvoltarea produselor software. Le multumesc
pentru aprecieri pro/contra asupra lucrării membrilor catedrei de informatică de la Facultatea de Ştiinţe Economice şi
Administraţie Publică.
Autorul,
Conf. univ. dr. Lupu Valeriu
Universitatea “Ştefan cel Mare” Suceava
Facultatea de Ştiinţe Economice şi Administraţie Publică
Catedra de Informatică
4

3. Cuprins
Capitolul I Descrierea algoritmilor .................................................................................. ...............
6
Capitolul II Subprograme ................................................................................................. .............1
6
Capitolul III Metode de proiectare a algoritmilor .............................................................. .............2
3
Capitolul IV Analiza algoritmilor ...................................................................................... .............2
7
Capitolul V Clase de algoritmi ........................................................................................... .............3
4
Capitolul VI Evoluţia limbajelor de programare ................................................................ .............4
1
Capitolul VII Limbajul Visual Basic ................................................................................... .............5
5
Capitolul VIII Reguli privind alegerea unui limbaj de programare ...................................... .............6
9
Capitolul IX Metoda backtracking ..................................................................................... .............7
3
Capitolul X Metoda Divide et impera ............................................................................... .............9
1
Capitolul XI Metoda Greedy .............................................................................................. .............9
5
Capitolul XII Studii de caz – Aplicaţii ................................................................................ ...........10
9
Bibliografie ......................................................................................................................... ...........13
5
5

4. CAPITOLUL I
DESCRIEREA ALGORITMILOR
1.1 Algoritm, program, programare
Apariţia primelor calculatoare electronice a constituit un salt uriaş în direcţia automatizării
activităţii umane. Nu există astăzi domeniu de activitate în care calculatorul să nu îşi arate utilitatea[18].
Calculatoarele pot fi folosite pentru a rezolva probleme, numai dacă pentru rezolvarea acestora se
concep programe corespunzătoare de rezolvare. Termenul de program (programare) a suferit schimbări în
scurta istorie a informaticii. Prin anii '60 problemele rezolvate cu ajutorul calculatorului erau simple şi se
găseau algoritmi nu prea complicaţi pentru rezolvarea lor. Prin program se înţelegea rezultatul scrierii
unui algoritm într-un limbaj de programare. Din cauza creşterii complexităţii problemelor, astăzi pentru
rezolvarea unei probleme adesea vom concepe un sistem de mai multe programe.
Dar ce este un algoritm? O definiţie matematică, riguroasă, este greu de dat, chiar imposibilă fără
a introduce şi alte noţiuni. Vom încerca în continuare o descriere a ceea ce se înţelege prin algoritm.
Ne vom familiariza cu această noţiune prezentând mai multe exemple de algoritmi şi observând ce
au ei în comun. Cel mai vechi exemplu este algoritmul lui Euclid, algoritm care determină cel mai mare
divizor comun a două numere naturale. Evident, vom prezenta mai mulţi algoritmi, cei mai mulţi fiind
legaţi de probleme accesibile absolvenţilor de liceu.
Vom constata că un algoritm este un text finit, o secvenţă finită de propoziţii ale unui limbaj. Din
cauză că este inventat special în acest scop, un astfel de limbaj este numit limbaj de descriere a
algoritmilor. Fiecare propoziţie a limbajului precizează o anumită regulă de calcul, aşa cum se va
observa atunci când vom prezenta limbajul Pseudocod.
Oprindu-ne la semnificaţia algoritmului, la efectul execuţiei lui, vom observa că fiecare algoritm
defineşte o funcţie matematică. De asemenea, din toate secţiunile următoare va reieşi foarte clar că un
algoritm este scris pentru rezolvarea unei probleme. Din mai multe exemple se va observa însă că, pentru
rezolvarea aceleaşi probleme, există mai mulţi algoritmi.
Pentru fiecare problemă P există date presupuse cunoscute (date iniţiale pentru algoritmul
corespunzător, A) şi rezultate care se cer a fi găsite (date finale). Evident, problema s-ar putea să nu aibă
sens pentru orice date iniţiale. Vom spune că datele pentru care problema P are sens fac parte din
domeniul D al algoritmului A. Rezultatele obţinute fac parte dintr-un domeniu R, astfel că executând
algoritmul A cu datele de intrare x∈D vom obţine rezultatele r∈R. Vom spune că A(x)=r şi astfel
algoritmul A defineşte o funcţie
A : D ---> R .
Algoritmii au următoarele caracteristici: generalitate, finitudine şi unicitate.
Prin generalitate se înţelege faptul că un algoritm este aplicabil pentru orice date iniţiale x∈D.
Deci un algoritm A nu rezolvă problema P cu nişte date de intrare, ci o rezolvă în general, oricare ar fi
aceste date. Astfel, algoritmul de rezolvare a unui sistem liniar de n ecuaţii cu n necunoscute prin metoda
lui Gauss, rezolvă orice sistem liniar şi nu un singur sistem concret.
Prin finitudine se înţelege că textul algoritmului este finit, compus dintr-un număr finit de
propoziţii. Mai mult, numărul transformărilor ce trebuie aplicate unei informaţii admisibile x∈D pentru a
obţine rezultatul final corespunzător este finit.
Prin unicitate se înţelege că toate transformările prin care trece informaţia iniţială pentru a obţine
rezultatul r∈R sunt bine determinate de regulile algoritmului. Aceasta înseamnă că fiecare pas din
execuţia algoritmului dă rezultate bine determinate şi precizează în mod unic pasul următor. Altfel spus,
ori de câte ori am executa algoritmul, pornind de la aceeaşi informaţie admisibilă x∈D, transformările
prin care se trece şi rezultatele obţinute sunt aceleaşi.
În descrierea algoritmilor se folosesc mai multe limbaje de descriere, dintre care cele mai des
folosite sunt:
- limbajul schemelor logice;
6

5. - limbajul Pseudocod.
În continuare vom folosi pentru descrierea algoritmilor limbajul Pseudocod care va fi definit în
cele ce urmează. În ultima vreme schemele logice sunt tot mai puţin folosite în descrierea algoritmilor şi
nu sunt deloc potrivite în cazul problemelor complexe. Prezentăm însă şi schemele logice, care se mai
folosesc în manualele de liceu, întrucât cu ajutorul lor vom preciza în continuare semantica propoziţiilor
Pseudocod.
1.2 Scheme logice
Schema logică este un mijloc de descriere a algoritmilor prin reprezentare grafică. Regulile de
calcul ale algoritmului sunt descrise prin blocuri (figuri geometrice) reprezentând operaţiile (paşii)
algoritmului, iar ordinea lor de aplicare (succesiunea operaţiilor) este indicată prin săgeţi. Fiecărui tip de
operaţie îi este consacrată o figură geometrică (un bloc tip) în interiorul căreia se va înscrie operaţia din
pasul respectiv.
Prin execuţia unui algoritm descris printr-o schemă logică se înţelege efectuarea tuturor
operaţiilor precizate prin blocurile schemei logice, în ordinea indicată de săgeţi.
În descrierea unui algoritm, deci şi într-o schemă logică, intervin variabile care marchează atât
datele cunoscute iniţial, cât şi rezultatele dorite, precum şi alte rezultate intermediare necesare în
rezolvarea problemei. Întrucât variabila joacă un rol central în programare este bine să definim acest
concept. Variabila defineşte o mărime care îşi poate schimba valoarea în timp. Ea are un nume şi,
eventual, o valoare. Este posibil ca variabila încă să nu fi primit valoare, situaţie în care vom spune că ea
este neiniţializată. Valorile pe care le poate lua variabila aparţin unei mulţimi D pe care o vom numi
domeniul variabilei. În concluzie vom înţelege prin variabilă tripletul
(nume, domeniul D, valoare)
unde valoare aparţine mulţimii D ∪ {nedefinit}.
Blocurile delimitatoare Start şi Stop (Fig.1.2.1. a şi 1.2.1. b) vor marca începutul respectiv
sfârşitul unui algoritm dat printr-o schemă logică. Descrierea unui algoritm prin schemă logică va începe
cu un singur bloc Start şi se va termina cu cel puţin un bloc Stop.
Blocurile de intrare/ieşire Citeşte şi Tipăreşte (Fig. 1.2.1. c şi d) indică introducerea unor Date
de intrare respectiv extragerea unor Rezultate finale. Ele permit precizarea datelor iniţiale cunoscute în
problemă şi tipărirea rezultatelor cerute de problemă. Blocul Citeşte iniţializează variabilele din lista de
intrare cu valori corespunzătoare, iar blocul Tipăreşte va preciza rezultatele obţinute (la execuţia pe
calculator cere afişarea pe ecran a valorilor expresiilor din lista de ieşire).
Blocurile de atribuire (calcul) se utilizează în descrierea operaţiilor de atribuire (:=). Printr-o
astfel de operaţie, unei variabile var i se atribuie valoarea calculată a unei expresii expr (Fig.1.2.1. e).
Fig.1.2.1. Blocurile schemelor logice
7

6. Blocurile de decizie marchează punctele de ramificaţie ale algoritmului în etapa de decizie. Ramificarea
poate fi dublă (blocul logic, Fig.1.2.1.f) sau triplă (blocul aritmetic, Fig. 1.2.1.g). Blocul de decizie logic
indică ramura pe care se va continua execuţia algoritmului în funcţie de îndeplinirea (ramura Da) sau
neîndeplinirea (ramura Nu) unei condiţii. Condiţia care se va înscrie în blocul de decizie logic va fi o
expresie logică a cărei valoare poate fi una dintre valorile "adevărat" sau "fals". Blocul de decizie
aritmetic va hotărî ramura de continuare a algoritmului în funcţie de semnul valorii expresiei aritmetice
înscrise în acest bloc, care poate fi negativă, nulă sau pozitivă.
Blocurile de conectare marchează întreruperile săgeţilor de legătură dintre blocuri, dacă din
diverse motive s-au efectuat astfel de întreruperi (Fig.1.2.1.h).
Pentru exemplificare vom da în continuare două scheme logice, corespunzătoare unor algoritmi
pentru rezolvarea problemelor P1.2.1 şi P1.2.2.
P1.2.1. Să se rezolve ecuaţia de grad doi aX2+bX+c=0 (a,b,c∈R _i a≠0).
Metoda de rezolvare a ecuaţiei de gradul doi este cunoscută. Ecuaţia poate avea rădăcini reale, respectiv
complexe, situaţie recunoscută după semnul discriminantului d = b2 - 4ac.
Fig.1.2.2. Algoritm pentru rezolvarea ecuaţiei de gradul doi Fig.1.2.3. Algoritm pentru calculul
unei sume.
Algoritmul de rezolvare a problemei va citi mai întâi datele problemei, marcate prin variabilele a,
b şi c. Va calcula apoi discriminantul d şi va continua în funcţie de valoarea lui d, aşa cum se poate vedea
în fig.1.2.2.
P1.2.2. Să se calculeze suma elementelor pozitive ale unui şir de numere reale dat.
Schema logică (dată în Fig.1.2.3) va conţine imediat după blocul START un bloc de citire, care
precizează datele cunoscute în problemă, apoi o parte care calculează suma cerută şi un bloc de tipărire a
sumei găsite, înaintea blocului STOP. Partea care calculează suma S cerută are un bloc pentru iniţializarea
8

7. cu 0 a acestei sume, apoi blocuri pentru parcurgerea numerelor: x1, x2…xn şi adunarea celor pozitive la
suma S. Pentru această parcurgere se foloseşte o variabilă contor i, care este iniţializată cu 1 şi creşte
mereu cu 1 pentru a atinge valoarea n, indicele ultimului număr dat.
Schemele logice dau o reprezentare grafică a algoritmilor cu ajutorul unor blocuri de calcul.
Execuţia urmează sensul indicat de săgeată, putând avea loc reveniri în orice punct din schema logică.
Din acest motiv se poate obţine o schemă logică încâlcită, greu de urmărit. Rezultă importanţa compunerii
unor scheme logice structurate (D-scheme, după Djikstra), care să conţină numai anumite structuri
standard de calcul şi în care drumurile de la START la STOP să fie uşor de urmărit.
1.3. Limbajul PSEUDOCOD
Limbajul Pseudocod este un limbaj inventat în scopul proiectării algoritmilor şi este format din
propoziţii asemănătoare propoziţiilor limbii române, care corespund structurilor de calcul folosite în
construirea algoritmilor. Acesta va fi limbajul folosit de noi în proiectarea algoritmilor şi va fi definit în
cele ce urmează. Ţinând seama că obţinerea unui algoritm pentru rezolvarea unei probleme nu este
întotdeauna o sarcină simplă, că în acest scop sunt folosite anumite metode pe care le vom descrie în
capitolele următoare, în etapele intermediare din obţinerea algoritmului vom folosi propoziţii curente din
limba română. Acestea sunt considerate elemente nefinisate din algoritm, asupra cărora trebuie să se
revină şi le vom numi propoziţii nestandard. Deci limbajul Pseudocod are două tipuri de propoziţii:
propoziţii standard, care vor fi prezentate fiecare cu sintaxa şi semnificaţia (semantica) ei şi propoziţii
nestandard. Aşa cum se va arăta mai târziu, propoziţiile nestandard sunt texte care descriu părţi ale
algoritmului încă incomplet elaborate, nefinisate, asupra cărora urmează să se revină.
Pe lângă aceste propoziţii standard şi nestandard, în textul algoritmului vom mai introduce
propoziţii explicative, numite comentarii. Pentru a le distinge de celelalte propoziţii, comentariile vor fi
închise între acolade. Rolul lor va fi explicat puţin mai târziu.
Propoziţiile standard ale limbajului Pseudocod folosite în această lucrare, corespund structurilor
de calcul prezentate în figura 1.3.1 şi vor fi prezentate în continuare. Fiecare propoziţie standard începe cu
un cuvânt cheie, aşa cum se va vedea în cele ce urmează. Pentru a deosebi aceste cuvinte de celelalte
denumiri, construite de programator, în acest capitol vom scrie cuvintele cheie cu litere mari. Menţionăm
că şi propoziţiile simple se termină cu caracterul ';' în timp ce propoziţiile compuse, deci cele în interiorul
cărora se află alte propoziţii, au un marcaj de sfârşit propriu. De asemenea, menţionăm că propoziţiile
limbajului Pseudocod vor fi luate în seamă în ordinea întâlnirii lor în text, asemenea oricărui text al limbii
române.
Prin execuţia unui algoritm descris în Pseudocod se înţelege efectuarea operaţiilor precizate de
propoziţiile algoritmului, în ordinea citirii lor.
În figura 1.3.1, prin A, B s-au notat subscheme logice, adică secvenţe de oricâte structuri
construite conform celor trei reguli menţionate în continuare.
Structura secvenţială (fig.1.3.1.a) este redată prin concatenarea propoziţiilor, simple sau
compuse, ale limbajului Pseudocod, care vor fi executate în ordinea întâlnirii lor în text.
a) structura b) structura c) structura
secvenţială alternativă repetitivă
Figura 1.3.1. Structurile elementare de calcul
9

8. Propoziţiile simple din limbajul Pseudocod sunt CITEŞTE, TIPAREŞTE, FIE şi apelul de
subprogram. Propoziţiile compuse corespund structurilor alternative şi repetitive.
Structura alternativă (fig.1.3.1.b) este redată în Pseudocod prin propoziţia DACĂ, prezentată în
secţiunea 1.3.2, iar structura repetitivă din fig.1.3.1.c este redată în Pseudocod prin propoziţia CÂT
TIMP, prezentată în secţiunea 1.3.3.
Bohm şi Jacopini au demonstrat că orice algoritm poate fi descris folosind numai aceste trei
structuri de calcul.
Propoziţiile DATE şi REZULTATE sunt folosite în faza de specificare a problemelor, adică
enunţarea riguroasă a acestora. Propoziţia DATE se foloseşte pentru precizarea datelor iniţiale, deci a
datelor considerate cunoscute în problemă (numite şi date de intrare) şi are sintaxa:
DATE listă;
unde listă conţine toate numele variabilelor a căror valoare iniţială este cunoscută. În general, prin listă se
înţelege o succesiune de elemente de acelaşi fel despărţite prin virgulă. Deci în propoziţia DATE, în
dreapta acestui cuvânt se vor scrie acele variabile care marchează mărimile cunoscute în problemă.
Pentru precizarea rezultatelor dorite se foloseşte propoziţia standard
REZULTATE listă;
în construcţia "listă" ce urmează după cuvântul REZULTATE fiind trecute numele variabilelor care
marchează (conţin) rezultatele cerute în problemă.
Acum putem preciza mai exact ce înţelegem prin cunoaşterea completă a problemei de rezolvat.
Evident, o problemă este cunoscută atunci când se ştie care sunt datele cunoscute în problemă şi ce
rezultate trebuiesc obţinute. Deci pentru cunoaşterea unei probleme este necesară precizarea variabilelor
care marchează date considerate cunoscute în problemă, care va fi reflectată printr-o propoziţie DATE şi
cunoaşterea exactă a cerinţelor problemei, care se va reflecta prin propoziţii REZULTATE. Variabilele
prezente în aceste propoziţii au anumite semnificaţii, presupuse cunoscute. Cunoaşterea acestora, scrierea
lor explicită, formează ceea ce vom numi în continuare specificarea problemei. Specificarea unei
probleme este o activitate foarte importantă dar nu şi simplă.
De exemplu, pentru rezolvarea ecuaţiei de gradul al doilea, specificarea problemei, scrisă de un
începător, poate fi:
DATE a,b,c; { Coeficienţii ecuaţiei }
REZULTATE x1,x2; { Rădăcinile ecuaţiei }
Această specificaţie este însă incompletă dacă ecuaţia nu are rădăcini reale. În cazul în care rădăcinile
sunt complexe putem nota prin x1, x2 partea reală respectiv partea imaginară a rădăcinilor. Sau pur şi
simplu, nu ne interesează valoarea rădăcinilor în acest caz, ci doar faptul că ecuaţia nu are rădăcini reale.
Cu alte cuvinte avem nevoie de un mesaj care să ne indice această situaţie (vezi schema logică 1.2.2), sau
de un indicator, fie el ind. Acest indicator va lua valoarea 1 dacă rădăcinile sunt reale şi valoarea 0 în caz
contrar. Deci specificaţia corectă a problemei va fi
DATE a,b,c; { Coeficienţii ecuaţiei }
REZULTATE ind, {Un indicator: 1=rădăcini reale, 0=complexe}
x1,x2; { Rădăcinile ecuaţiei, în cazul ind=1,}
{respectiv partea reală şi cea }
{imaginară în cazul ind=0}
Evident că specificarea problemei este o etapă importantă pentru găsirea unei metode de rezolvare
şi apoi în proiectarea algoritmului corespunzător. Nu se poate rezolva o problemă dacă aceasta nu este
bine cunoscută, adică nu avem scrisă specificarea problemei. Cunoaşte complet problema este prima
regulă ce trebuie respectată pentru a obţine cât mai repede un algoritm corect pentru rezolvarea ei.
1.3.1 Algoritmi liniari
Propoziţiile CITEŞTE şi TIPĂREŞTE sunt folosite pentru iniţializarea variabilelor de intrare cu
datele cunoscute în problemă, respectiv pentru tipărirea (aflarea) rezultatelor obţinute. În etapa de
10

9. programare propriu-zisă acestor propoziţii le corespund într-un limbaj de programare instrucţiuni de
intrare-ieşire.
Propoziţia CITEŞTE se foloseşte pentru precizarea datelor iniţiale, deci a datelor considerate
cunoscute în problemă (numite şi date de intrare) şi are sintaxa:
CITEŞTE listă ;
unde listă conţine toate numele variabilelor a căror valoare iniţială este cunoscută.
Deci în propoziţia CITEŞTE, în dreapta acestui cuvânt se vor scrie acele variabile care apar în
propoziţia DATE în specificarea problemei. Se subînţelege că aceste variabile sunt iniţializate cu valorile
cunoscute corespunzătoare.
Pentru aflarea rezultatelor dorite, pe care calculatorul o va face prin tipărirea lor pe hârtie sau
afişarea pe ecran, se foloseşte propoziţia standard
TIPĂREŞTE listă ;
în construcţia listă ce urmează după cuvântul TIPĂREŞTE fiind trecute numele variabilelor a căror
valori dorim să le aflăm. Ele sunt de obicei rezultatele cerute în problemă, specificate şi în propoziţia
REZULTATE.
Blocului de atribuire dintr-o schemă logică îi corespunde în Pseudocod propoziţia standard
[FIE] var := expresie ;
Această propoziţie este folosită pentru a indica un calcul algebric, al expresiei care urmează după
simbolul de atribuire ":=" şi de atribuire a rezultatului obţinut variabilei var. Expresia din dreapta
semnului de atribuire poate fi orice expresie algebrică simplă, cunoscută din manualele de matematică din
liceu şi construită cu cele patru operaţii: adunare, scădere, înmulţire şi împărţire (notate prin caracterele +,
-, *, respectiv /).
Prin scrierea cuvântului FIE între paranteze drepte se indică posibilitatea omiterii acestui cuvânt
din propoziţie. El s-a folosit cu gândul ca fiecare propoziţie să înceapă cu un cuvânt al limbii române care
să reprezinte numele propoziţiei. De cele mai multe ori vom omite acest cuvânt. Atunci când vom scrie
succesiv mai multe propoziţii de atribuire vom folosi cuvântul FIE numai în prima propoziţie, omiţându-l
în celelalte.
Din cele scrise mai sus rezultă că o variabilă poate fi iniţializată atât prin atribuire (deci dacă este
variabila din stânga semnului de atribuire :=) cât şi prin citire (când face parte din lista propoziţiei
CITEŞTE). O greşeală frecventă pe care o fac începătorii este folosirea variabilelor neiniţializate.
Evident că o expresie în care apar variabile care nu au valori nu poate fi calculată, ea nu este definită.
Deci nu folosiţi variabile neiniţializate.
Pentru a marca începutul descrierii unui algoritm vom folosi propoziţia:
ALGORITMUL nume ESTE:
fără a avea o altă semnificaţie. De asemenea, prin cuvântul SFALGORITM vom marca sfârşitul unui
algoritm.
Algoritmii care pot fi descrişi folosind numai propoziţiile prezentate mai sus se numesc algoritmi
liniari.
Ca exemplu de algoritm liniar prezentăm un algoritm ce determină viteza v cu care a mers un
autovehicul ce a parcurs distanţa D în timpul T.
ALGORITMUL VITEZA ESTE: { A1: Calculează viteza }
{ D = Distanţa (spaţiul) }
{ T = Timpul; V = Viteza }
CITEŞTE D,T; { v:= spaţiu/timp }
FIE V:=D/T;
TIPĂREŞTE V
SFALGORITM
11

10. 1.3.2 Algoritmi cu ramificaţii
Foarte mulţi algoritmi execută anumite calcule în funcţie de satisfacerea unor condiţii. Aceste
calcule sunt redate de structura alternativă prezentată în figura 1.3.1.b, căreia îi corespunde propoziţia
Pseudocod
DACĂ cond ATUNCI A ALTFEL B SFDACĂ
sau varianta redusă a ei, DACĂ cond ATUNCI A SFDACĂ
folosită în cazul în care grupul de propoziţii B este vid.
Aceste propoziţii redau în Pseudocod structura alternativă de calcul. Ele cer mai întâi verificarea
condiţiei scrise după cuvântul DACĂ. În caz că această condiţie este adevărată se va executa grupul de
propoziţii A. În cazul în care această condiţie este falsă se va executa grupul de propoziţii B, dacă este
prezentă ramura ALTFEL. Indiferent care dintre secvenţele A sau B a fost executată, se va continua cu
propoziţia următoare propoziţiei DACĂ.
O generalizare a structurii alternative realizată de propoziţia DACĂ este structura selectivă:
SELECTEAZĂ i DINTRE
v1: A1;
v2: A2;
...
vn: An
SFSELECTEAZĂ
structură echivalentă cu următorul text Pseudocod:
DACĂ i=v1 ATUNCI A1 ALTFEL
DACĂ i=v2 ATUNCI A2 ALTFEL
. . .
DACĂ i=vn ATUNCI An SFDACĂ
. . .
SFDACĂ
SFDACĂ
Cu propoziţiile prezentate până aici putem deja descrie destui algoritmi. Aceştia se numesc
algoritmi cu ramificaţii.
Ca exemplu vom scrie un algoritm pentru rezolvarea ecuaţiei de gradul al doilea. Am scris mai sus
specificaţia acestei probleme şi am precizat semnificaţia variabilelor respective. Pe lângă aceste variabile,
pentru rezolvarea problemei mai avem nevoie de două variabile auxiliare:
delta - pentru a reţine discriminantul ecuaţiei;
r - pentru a reţine valoarea radicalului folosit în exprimarea rădăcinilor.
Ajungem uşor la algoritmul dat în continuare.
ALGORITMUL ECGRDOI ESTE: { Algoritmul 2: Rezolvarea }
{ ecuaţiei de gradul doi }
CITEŞTE a,b,c; { a,b,c = Coeficienţii ecuaţiei }
FIE delta:=b*b- 4*a*c;
DACĂ delta<0 ATUNCI ind:=0; { rădăcini complexe }
r:=radical din (- delta);
x1:=- b/(a+a);
x2:=r/(a+a);
ALTFEL ind:=1; { rădăcini reale }
r:=radical din delta;
x1:=(-b- r)/(a+a);
x2:=(-b+r)/(a+a);
SFDACĂ
TIPĂREŞTE ind, x1,x2;
SFALGORITM
12

11. 1.3.3 Algoritmi ciclici
În rezolvarea multor probleme trebuie să efectuăm aceleaşi calcule de mai multe ori, sau să
repetăm calcule asemănătoare. De exemplu, pentru a calcula suma a două matrice va trebui să adunăm un
element al primei matrice cu elementul de pe aceeaşi poziţie din a doua matrice, această adunare
repetându-se pentru fiecare poziţie. Alte calcule trebuiesc repetate în funcţie de satisfacerea unor condiţii.
În acest scop în limbajul Pseudocod există trei propoziţii standard: CÂTTIMP, REPETĂ şi PENTRU.
Propoziţia CÂTTIMP are sintaxa CÂTTIMP cond EXECUTĂ A SFCÂT
i cere execuţia repetată a grupului de propoziţii A, în funcţie de condiţia "cond". Mai exact, se evaluează
condiţia "cond"; dacă aceasta este adevărată se execută grupul A şi se revine la evaluarea condiţiei. Dacă
ea este falsă execuţia propoziţiei se termină şi se continuă cu propoziţia care urmează după SFCÂT. Dacă
de prima dată condiţia este falsă grupul A nu se va executa niciodată, altfel se va repeta execuţia grupului
de propoziţii A până când condiţia va deveni falsă. Din cauză că înainte de execuţia grupului A are loc
verificarea condiţiei, această structură se mai numeşte structură repetitivă condiţionată anterior. Ea
reprezintă structura repetitivă prezentată în figura 1.3.1.c.
Ca exemplu de algoritm în care se foloseşte această propoziţie dăm algoritmul lui Euclid pentru
calculul celui mai mare divizor comun a două numere.
ALGORITMUL Euclid ESTE: {A3: Cel mai mare divizor comun}
CITEŞTE n1,n2; {Cele două numere a căror divizor se cere}
FIE d:=n1; i:=n2;
CÂTTIMP i≠0 EXECUTĂ
r:=d modulo i; d:=i; i:=r
SFCÂT
TIPĂREŞTE d; { d= cel mai mare divizor comun al }
SFALGORITM { numerelor n1 şi n2 }
În descrierea multor algoritmi se întâlneşte structura repetitivă condiţionată posterior:
REPETĂ A PÂNĂ CÂND cond SFREP
structură echivalentă cu: CÂTTIMP not(cond) EXECUTĂ A SFCÂT
Deci ea cere execuţia necondiţionată a lui A şi apoi verificarea condiţiei "cond". Va avea loc
repetarea execuţiei lui A până când condiţia devine adevărată. Deoarece condiţia se verifică după prima
execuţie a grupului A această structură este numită structura repetitivă condiţionată posterior, prima
execuţie a blocului A fiind necondiţionată.
O altă propoziţie care cere execuţia repetată a unei secvenţe A este propoziţia
PENTRU c:=li ;lf [;p] EXECUTĂ A SFPENTRU
Ea defineşte structura repetitivă predefinită, cu un număr determinat de execuţii ale grupului de
propoziţii A şi este echivalentă cu secvenţa
c:=li ; final:=lf ;
REPETĂ
A
c:=c+p
PÂNĂCÂND (c>final şi p>0) sau (c<final şi p<0) SFREP
Se observă că, în sintaxa propoziţiei PENTRU, pasul p este închis între paranteze drepte. Prin
aceasta indicăm faptul că el este opţional, putând să lipsească. În cazul în care nu este prezent, valoarea
lui implicită este 1.
Semnificaţia propoziţiei PENTRU este clară. Ea cere repetarea grupului de propoziţii A pentru
toate valorile contorului c cuprinse între valorile expresiilor li şi lf (calculate o singură dată înainte de
începerea ciclului), cu pasul p. Se subînţelege că nu trebuie să modificăm valorile contorului în nici o
propoziţie din grupul A. De multe ori aceste expresii sunt variabile simple, iar unii programatori modifică
în A valorile acestor variabile, încălcând semnificaţia propoziţiei PENTRU. Deci, nu recalcula limitele
şi nu modifica variabila de ciclare (contorul) în interiorul unei structuri repetitive PENTRU).
13

12. Să observăm, de asemenea, că prima execuţie a grupului A este obligatorie, abia după modificarea
contorului verificându-se condiţia de continuare a execuţiei lui A.
Ca exemplu, să descriem un algoritm care găseşte minimul şi maximul componentelor unui vector
de numere reale. Vom nota prin X acest vector, deci X = (x1, x2, ... , xn) .
Specificaţia problemei este următoarea:
DATE n,(xi ,i=1,n);
REZULTATE valmin,valmax;
iar semnificaţia acestor variabile se înţelege din cele scrise mai sus. Pentru rezolvarea problemei vom
examina pe rând cele n componente. Pentru a parcurge cele n componente avem nevoie de un contor care
să precizeze poziţia la care am ajuns. Fie i acest contor. Uşor se ajunge la următorul algoritm:
ALGORITMUL MAXMIN ESTE { Algoritmul 5: Calculul }
{ valorii minime şi maxime }
CITEŞTE n,(xi,i=1,n);
FIE valmin:=x1; valmax:=x1;
PENTRU i:=2,n EXECUTĂ
DACĂ xi<valmin ATUNCI valmin:=xi SFDACĂ
DACĂ xi>valmax ATUNCI valmax:=xi SFDACĂ
SFPENTRU
TIPĂREŞTE valmin,valmax;
SFALGORITM
Un rol important în claritatea textului unui algoritm îl au denumirile alese pentru variabile. Ele
trebuie să reflecte semnificaţia variabilelor respective. Deci alege denumiri sugestive pentru variabile,
care să reflecte semnificaţia lor.
În exemplul de mai sus denumirile valmin şi valmax spun cititorului ce s-a notat prin aceste
variabile.
1.4 Calculul efectuat de un algoritm
Fie X1, X2, ..., Xn, variabilele ce apar în algoritmul A. În orice moment al execuţiei algoritmului,
fiecare variabilă are o anumită valoare, sau este încă neiniţializată.
Vom numi stare a algoritmului A cu variabilele menţionate vectorul
s = ( s1,s2,...,sn )
format din valorile curente ale celor n variabile ale algoritmului.
Este posibil ca variabila Xj să fie încă neiniţializată, deci să nu aibă valoare curentă, caz în care sj
este nedefinită, lucru notat în continuare prin semnul întrebării '?'.
Prin executarea unei anumite instrucţiuni unele variabile îşi schimbă valoarea, deci algoritmul îşi
schimbă starea.
Se numeşte calcul efectuat de algoritmul A o secvenţă de stări
s0, s1, s2, ..., sm
unde s0 este starea iniţială cu toate variabilele neiniţializate, iar sm este starea în care se ajunge după
execuţia ultimei propoziţii din algoritm.
1.5 Rafinare în paşi succesivi
Adeseori algoritmul de rezolvare a unei probleme este rezultatul unui proces complex, în care se
iau mai multe decizii şi se precizează tot ceea ce iniţial era neclar. Observaţia este adevărată mai ales în
cazul problemelor complicate, dar şi pentru probleme mai simple în procesul de învăţământ. Este vorba
de un proces de detaliere pas cu pas a specificaţiei problemei, proces denumit şi proiectare descendentă,
sau rafinare în paşi succesivi. Algoritmul apare în mai multe versiuni succesive, fiecare versiune fiind o
detaliere a versiunii precedente. În versiunile iniţiale apar propoziţii nestandard, clare pentru cititor, dar
14

13. neprecizate prin propoziţii standard. Urmează ca în versiunile următoare să se revină asupra lor.
Algoritmul apare astfel în versiuni succesive, tot mai complet de la o versiune la alta.
Apare aici o altă regulă importantă în proiectarea algoritmului: amână pe mai târziu detaliile
nesemnificative; concentrează-ţi atenţia la deciziile importante ale momentului.
15

14. CAPITOLUL II
SUBPROGRAME
Conceptul de SUBPROGRAM
Orice problemă poate apare ca o subproblemă S a unei probleme mai complexe C. Algoritmul de
rezolvare a problemei S devine în acest caz un SUBPROGRAM pentru algoritmul de rezolvare a
problemei C.
Pentru a defini un SUBPROGRAM vom folosi propoziţia standard
SUBPROGRAMUL nume (lpf) ESTE:
unde nume este numele SUBPROGRAMului definit, iar lpf este lista parametrilor formali. Aceştia sunt
formaţi din variabilele care marchează datele de intrare (cele presupuse cunoscute) şi variabilele care
marchează datele de ieşire (rezultatele obţinute de SUBPROGRAM).
Această propoziţie este urmată de textul efectiv al SUBPROGRAMului, text care precizează
calculele necesare rezolvării subproblemei corespunzătoare. Descrierea se va încheia cu cuvântul
SFSUBPROGRAM sau SF-nume.
Dăm ca exemplu un SUBPROGRAM cu numele MAXIM, care găseşte maximul dintre
componentele vectorului X = (x1,x2, ..., xn).
Datele cunoscute pentru acest SUBPROGRAM sunt vectorul X şi numărul n al componentelor
vectorului X. Ca rezultat vom obţine maximul cerut, pe care-l vom nota cu max. Deci lista parametrilor
formali conţine trei variabile, n, X şi max. SUBPROGRAMul este dat în continuare.
SUBPROGRAMUL maxim(n,X,max) ESTE:
FIE max:=x1;
PENTRU i:=2;n EXECUTĂ
DACĂ xi>max ATUNCI max:=xi SFDACĂ
SFPENTRU
SF-maxim
În cadrul multor algoritmi este necesar calculul valorilor unei funcţii în diferite puncte. Este
necesar să definim funcţia printr-un SUBPROGRAM de tip funcţie.
Pentru definirea unui SUBPROGRAM de tip funcţie se foloseşte un antet care precizează
numele funcţiei şi variabilele de care depinde ea. SUBPROGRAMul are forma:
FUNCŢIA nume(lpf) ESTE: {Antetul funcţiei}
text {corpul funcţiei}
SF-nume {marca de sfârşit}
În corpul funcţiei trebuie să existe cel puţin o atribuire în care numele funcţiei apare în partea
stângă, deci prin care funcţia primeşte o valoare.
Dăm ca exemplu o funcţie numar : R --> {2,3,4,5}, definită matematic astfel:
În Pseudocod descrierea este următoarea:
FUNCŢIA numar(x) ESTE:
DACĂ x<0.2 ATUNCI numar:=2 ALTFEL
DACĂ x<0.5 ATUNCI numar:=3 ALTFEL
DACĂ x<0.9 ATUNCI numar:=4
ALTFEL numar:=5
SFDACĂ
SFDACĂ
SFDACĂ
SF-numar
16

15. Am văzut că definiţia unei funcţii constă dintr-un antet şi dintr-un bloc care va defini acţiunile
prin care se calculează valoarea funcţiei. În antet se precizează numele funcţiei şi lista parametrilor
formali.
În concluzie, există două categorii de SUBPROGRAMi: de tip funcţie şi SUBPROGRAMi
propriu-zişi, cărora li se mai spune şi proceduri. Importanţa lor va fi subliniată prin toate exemplele care
urmează în acest curs. În încheiere menţionăm că subprogramele de tip funcţie se folosesc în scopul
definirii funcţiilor, aşa cum sunt cunoscute ele din matematică, în timp ce SUBPROGRAMii de tip
procedură se referă la rezolvarea unor probleme ce apar ca subprobleme, fiind algoritmi de sine stătători.
Apelul unui SUBPROGRAM
Am văzut că un SUBPROGRAM este dedicat rezolvării unei subprobleme S a unei probleme mai
complexe C. Algoritmul corespunzător problemei C va folosi toate operaţiile necesare rezolvării
problemei S, deci va folosi ca parte întregul SUBPROGRAM conceput pentru rezolvarea subproblemei S.
Spunem că el va apela acest SUBPROGRAM.
În Pseudocod apelul unei funcţii se face scriind într-o expresie numele funcţiei urmat de lista
parametrilor actuali. Trebuie să existe o corespondenţă biunivocă între parametrii actuali şi cei formali
folosiţi în definiţia funcţiei. Deşi denumirile variabilelor din cele două liste pot să difere, rolul variabilelor
care se corespund este acelaşi. Mai exact, parametrul formal şi parametrul actual corespunzător trebuie să
se refere la aceeaşi entitate, trebuie să aibă aceeaşi semnificaţie, să reprezinte aceeaşi structură de date.
Putem considera că în timpul execuţiei algoritmului cei doi parametri devin identici.
Folosirea unui SUBPROGRAM în cadrul unui algoritm se face apelând acest SUBPROGRAM
prin propoziţia standard CHEAMĂ nume (lpa);
unde nume este numele SUBPROGRAMului apelat iar lpa este lista parametrilor actuali. Această listă
conţine toate datele de intrare (cele cunoscute în subproblema corespunzătoare) şi toate rezultatele
obţinute în SUBPROGRAM. Şi în acest caz între lista parametrilor formali din definiţia
SUBPROGRAMului şi lista parametrilor actuali din propoziţia de apel trebuie să existe o corespondenţă
biunivocă, ca şi în cazul funcţiilor. Ca o primă verificare a respectării acestei corespondenţe, subliniem că
numărul parametrilor actuali trebuie să coincidă cu numărul parametrilor formali.
Ca exemplu de apelare a funcţiilor, dăm în continuare un program pentru a calcula a câta zi din
anul curent este ziua curentă (zi,luna,an). El foloseşte un subprogram de tip funcţie pentru a obţine
numărul zilelor lunii cu numărul de ordine i şi un altul pentru a verifica dacă un an este bisect sau nu.
Aceste două funcţii sunt:
- NRZILE(i) furnizează numărul zilelor existente în luna i a unui an nebisect;
- BISECT(an) adevărată dacă anul dintre paranteze este bisect.
Algoritmul este următorul:
ALGORITMUL NUMĂRĂZILE ESTE:
CITEŞTE zi, luna, an;
FIE nr:=zi;
DACĂ luna>1 ATUNCI
PENTRU i:=1, Luna-1 EXECUTĂ nr:=nr+NRZILE(i) SFPENTRU
SFDACĂ
DACĂ luna>2 ATUNCI
DACĂ BISECT(an) ATUNCI nr:=nr+1 SFDACĂ
SFDACĂ
TIPĂREŞTE nr;
SFALGORITM
Să observăm că în proiectarea acestui algoritm nu este necesar să cunoaştem textul
SUBPROGRAMilor folosiţi, ci doar specificarea acestor SUBPROGRAMi, numele lor şi lista
parametrilor formali. La acest nivel accentul trebuie să cadă pe proiectarea algoritmului care apelează,
17

16. urmând să se revină ulterior la proiectarea SUBPROGRAMilor apelaţi, conform specificaţiei acestora. În
cazul de faţă este necesară descrierea funcţiilor NRZILE(i) şi BISECT(an). Lăsăm această descriere ca
temă pentru cititor.
Ca exemplu de apelare a unei proceduri vom scrie mai jos o procedură care efectuează suma a
două polinoame.
Un polinom P(X) este dat prin gradul său, m, şi prin vectorul coeficienţilor P = (p0, p1, ..., pm) (prin pi s-a
notat coeficientul lui Xi).
Procedura SUMAPOL(m,P,n,Q,r,S) trebuie să efectueze suma S(X) = P(X)+Q(X),
unde P este un polinom de gradul m, iar Q este un polinom de gradul n, date. Suma lor, S, va fi un
polinom de gradul r calculat în SUBPROGRAM. Pentru efectuarea ei este utilă o altă procedură care
adună la suma S(X) un alt polinom, T(X), de grad mai mic sau egal decât gradul polinomului S(X). O
astfel de procedură se dă în continuare.
SUBPROGRAMUL SUMAPOL1(n,T,r,S) ESTE: {n ≤ r}
{S(X):=S(X)+T(X)}
PENTRU i:=0;n EXECUTĂ
si := si+ti
SFPENTRU
SF-SUMAPOL1
SUBPROGRAMul SUMAPOL apelează acest SUBPROGRAM, aşa cum se poate vedea în
continuare.
SUBPROGRAMUL SUMAPOL(m,P,n,Q,r,S) ESTE: {S(X):=P(X)+Q(X)}
DACĂ m<n
ATUNCI r:=n; S:=Q;
CHEAMĂ SUMAPOL1(m,P,r,S)
ALTFEL r:=m; S:=P;
CHEAMĂ SUMAPOL1(n,Q,r,S)
SFDACĂ
SF-SUMAPOL
Să observăm că în textul acestui SUBPROGRAM am extins semnificaţia propoziţiei de atribuire,
permiţând atribuirea S:=Q. Acest lucru este normal întrucât S notează un polinom, iar Q este un polinom
cunoscut; prin atribuire S primeşte o valoare iniţială, cea dată de polinomul Q.
Subliniem că atribuirea v := u
va fi corectă în cazul în care variabilele u şi v reprezintă aceleaşi obiecte matematice, deci au aceeaşi
semnificaţie.
Alte exemple
Ca un al doilea exemplu de definire şi folosire a SUBPROGRAMilor, să considerăm următoarea
problemă:
Se dau trei mulţimi de numere:
A = { a1, a2, ... , am }
B = { b1, b2, ... , bn }
C = { c1, c2, ... , cp }
Se cere să se tipărească în ordine crescătoare elementele fiecărei mulţimi, precum şi a mulţimilor
A U B, B U C, C U A.
În rezolvarea acestei probleme se întâlnesc următoarele subprobleme:
S1: Să se citească elementele unei mulţimi;
S2: Să se efectueze reuniunea a două mulţimi;
S3: Să se tipărească elementele unei mulţimi;
S4: Să se ordoneze crescător elementele unei mulţimi.
Presupunând că pentru rezolvarea acestor subprobleme am conceput SUBPROGRAMii:
18

17. CITMUL(m,A);
REUNIUNE(m,A,n,B,k,R);
TIPMUL(m,A);
ORDON(m,A);
care sunt specificaţi mai jos (la locul definirii lor) prin comentarii, algoritmul de rezolvare a problemei de
mai sus este dat în continuare. Întrucât operaţiile respective se folosesc de mai multe ori (de 3 ori), am
definit un SUBPROGRAM TIPORDON(m,A) care ordonează mai întâi elementele mulţimii A şi apoi le
tipăreşte.
ALGORITMUL OPER-MULTIMI ESTE: { A6: SUBPROGRAMi }
CHEAMĂ CITMUL(m,A);
CHEAMĂ CITMUL(n,B);
CHEAMĂ CITMUL(p,C);
CHEAMĂ TIPORDON(m,A);
CHEAMĂ TIPORDON(n,B);
CHEAMĂ TIPORDON(p,C);
CHEAMĂ REUNIUNE(m,A,n,B,k,R);
CHEAMĂ TIPORDON(k,R);
CHEAMĂ REUNIUNE(n,B,p,C,k,R);
CHEAMĂ TIPORDON(k,R);
CHEAMĂ REUNIUNE(p,C,m,A,k,R);
CHEAMĂ TIPORDON(k,R);
SFALGORITM
SUBPROGRAMii apelaţi mai sus sunt definiţi în continuare.
SUBPROGRAMUL CITMUL(n,M) ESTE: {Citeşte n şi M}
CITEŞTE n; {n=nr. elementelor mulţimii}
CITEŞTE (mi,i=1,n); {M=mulţimea cu elementele m1,m2,...,mn}
SF-CITMUL
SUBPROGRAMUL ORDON(n,M) ESTE: {Ordonează crescător cele n}
REPETĂ {elemente ale mulţimii M}
FIE ind:=0; {Cazul M este ordonată}
PENTRU i:=1;n- 1 EXECUTĂ
DACĂ mi>mi+1 ATUNCI {schimbă ordinea celor}
FIE t := mi; {două elemente}
mi:=mi+1; mi+1:=t;
ind:=1; {Cazul M nu era ordonată}
SFDACĂ
SFPENTRU
PÂNĂCÂND ind=0 SFREP
SF-ORDON
SUBPROGRAMUL REUNIUNE(m,A,n,B,k,R) ESTE: { R := A U B }
{ k = numărul elementelor mulţimii R }
FIE k:=m; R := A;
PENTRU j:=1,n EXECUTĂ
FIE ind:=0; {Ipoteza bj nu e in A}
PENTRU i:=1;m EXECUTĂ
DACĂ bj=ai ATUNCI ind:=1 {bj este in A} SFDACĂ
SFPENTRU
19

18. DACĂ ind=0 ATUNCI k:=k+1; rk:=bj SFDACĂ
SFPENTRU
SF-REUNIUNE
SUBPROGRAMUL TIPMUL(n,M) ESTE: { Tipăreşte cele n elemente }
PENTRU i:=1;n EXECUTĂ { ale mulţimii M }
TIPĂREŞTE mi
SFPENTRU
SF-TIPMUL
SUBPROGRAMUL TIPORDON(n,M) ESTE: { Ordonează şi tipăreşte }
CHEAMĂ ORDON(n,M); { elementele mulţimii M }
CHEAMĂ TIPMUL(n,M);
SF-TIPORDON
Tot ca exemplu de folosire a SUBPROGRAMilor, vom scrie un algoritm pentru rezolvarea
următoarei probleme:
dirigintele unei clase de elevi doreşte să obţină un clasament al elevilor în funcţie de media generală. În
plus, pentru fiecare disciplină în parte doreşte lista primilor şase elevi.
În rezolvarea acestei probleme este necesară găsirea ordinii în care trebuiesc tipăriţi elevii în
funcţie de un anumit rezultat: nota la disciplina "j", sau media generală. Am identificat prin urmare două
subprobleme independente, referitoare la:
(1) aflarea ordinii în care trebuie tipărite n numere pentru a le obţine ordonate;
(2) tipărirea elevilor clasei într-o anumită ordine.
Prima subproblemă se poate specifica astfel:
Dându- se numerele x1, x2, ... , xn, găsiţi ordinea o1, o2, ..., on, în care aceste numere devin ordonate
descrescător, adică
x[o1] ≥ x[o2] ≥ ... x[on] .
Pentru rezolvarea ei vom da un SUBPROGRAM ORDINE în care intervin trei parametri formali:
- n, numărul valorilor existente;
- X, vectorul acestor valori;
- O, vectorul indicilor care dau ordinea dorită.
Primii doi parametri marchează datele presupuse cunoscute, iar al treilea, rezultatele calculate de
SUBPROGRAM.
SUBPROGRAMUL ORDINE(n,X,O) ESTE:
{n, numărul valorilor existente}
{X, vectorul acestor valori}
{O, vectorul indicilor care dau ordinea dorită}
PENTRU i:=1; n EXECUTĂ oi :=i SFPENTRU
REPETĂ ind:=0;
PENTRU i:=1;n- 1 EXECUTĂ
DACĂ x[oi] < x[oi+1] ATUNCI
FIE ind:=1; t:=oi+1 ;
oi+1 :=oi; oi :=t;
SFDACĂ
SFPENTRU
PANÂCÂND ind=0 SFREP
SF-ORDINE
A doua subproblemă se poate specifica astfel:
20

19. Dându- se ordinea o1,o2, ..., on, a elevilor clasei, numele şi mediile acestora, să se tipărească
numele şi mediile primilor k elevi în ordinea specificată.
SUBPROGRAMul TIPAR, dat în continuare, rezolvă această problemă.
SUBPROGRAMUL TIPAR(k, NUME, O) ESTE:
PENTRU i:=1;k EXECUTĂ
Tipăreşte datele elevului de rang oi.
SFPENTRU
SF-TIPAR
Variabilele folosite pentru problema dată sunt următoarele:
- n reprezintă numărul elevilor clasei;
- m este numărul disciplinelor la care elevii primesc note;
- NUME este vectorul care reţine numele elevilor: NUMEi este numele elevului cu numărul
de ordine i;
- NOTE este matricea notelor elevilor, având n linii şi m coloane;
NOTEi,j este nota elevului cu numele NUMEi la disciplina cu numărul de ordine j;
NOTE.j este coloana a j-a a matricei NOTE şi reprezintă notele elevilor la disciplina
j;
- MEDII este vectorul mediilor generale.
Algoritmul se dă în continuare:
ALGORITMUL CLASAMENT ESTE: { Algoritmul 7: Ordonare}
CITEŞTE m, {numărul disciplinelor şi}
n, {al elevilor}
NUMEi, i=1,n, {numele elevilor}
NOTEi,j, j=1,m, i=1,n; {notele elevilor}
PENTRU i:=1;n EXECUTĂ { calculează media generală}
FIE S:=0; {a elevului i}
PENTRU j:=1;m EXECUTĂ S:=S+NOTEi,j SFPENTRU
FIE MEDIIi:=S/m
SFPENTRU
CHEAMĂ ORDINE(n,MEDII,O);
CHEAMĂ TIPAR(n,NUME,O);
PENTRU j:=1;m EXECUTĂ
CHEAMĂ ORDINE(n,NOTE.j,O);
CHEAMĂ TIPAR(6,NUME,O);
SFPENTRU
SF-ALGORITM
Apel recursiv
În exemplele date se observă că apelul unui subprogram se face după ce el a fost definit. Este însă
posibil ca un SUBPROGRAM să se apeleze pe el însuşi. Într-un astfel de caz spunem că apelul este
recursiv, iar SUBPROGRAMul respectiv este definit recursiv.
Ca exemplu, definim în continuare o funcţie care calculează recursiv valoarea n!. Se va folosi
formula n! = n.(n- 1)! în cazul n>0 şi faptul că 0!=1. Recursivitatea constă în faptul că în definiţia funcţiei
Factorial de n se foloseşte aceeaşi funcţie Factorial dar de argument n-1. Deci funcţia Factorial se
apelează pe ea însăşi. Este important ca numărul apelurilor să fie finit, deci ca procedeul de calcul descris
să se termine.
FUNCTIA Factorial(n) ESTE:
DACĂ n=0 ATUNCI Factorial:=1
ALTFEL Factorial:= n*Factorial(n- 1)
21

20. SFDACĂ
SF-Factorial;
Tot ca exemplu de apel recursiv putem descrie o funcţie ce calculează maximul a n numere
x1,x2,...,xn. Ea se bazează pe funcţia MAXIM2 care calculează maximul a două numere, descrisă în
continuare.
FUNCŢIA MAXIM2(a,b) ESTE:
DACĂ a<b ATUNCI MAXIM2:=b
ALTFEL MAXIM2:=a
SFDACĂ
SF-MAXIM2
Funcţia MAXIM, care calculează maximul celor n numere este următoarea:
FUNCŢIA MAXIM(n,X) ESTE: {Calculează maximul a n numere}
{X=vectorul cu numerele date}
DACĂ n=1
ATUNCI MAXIM:=x1
ALTFEL MAXIM:=MAXIM2( MAXIM(n-1,X), xn)
SFDACĂ
SF-MAXIM
22

21. CAPITOLUL III
METODE DE PROIECTARE A ALGORITMILOR
3.1 Elaborarea algoritmilor
Prin elaborarea (proiectarea) unui algoritm înţelegem întreaga activitate depusă de la enunţarea
problemei până la realizarea algoritmului corespunzător rezolvării acestei probleme.
În elaborarea unui algoritm deosebim următoarele activităţi importante:
– specificarea problemei;
– descrierea metodei alese pentru rezolvarea problemei;
– proiectarea propriu-zisă. Ea constă în descompunerea problemei în subprobleme,
obţinerea algoritmului principal şi a tuturor SUBPROGRAMilor apelaţi, conform
metodelor prezentate în secţiunile următoare. Ea se termină cu descrierea algoritmului
principal şi a SUBPROGRAMilor menţionaţi, dar şi cu precizarea denumirilor şi
semnificaţiilor variabilelor folosite;
– verificarea algoritmului obţinut.
3.2 Proiectarea ascendentă şi proiectarea descendentă
Există două metode generale de proiectare a algoritmilor, a căror denumire provine din modul de
abordare a rezolvării problemelor: metoda descendentă şi metoda ascendentă. Proiectarea descendentă
(top-down) porneşte de la problema de rezolvat, pe care o descompune în părţi rezolvabile separat. De
obicei aceste părţi sunt subprobleme independente, care la rândul lor pot fi descompuse în subprobleme.
La prima descompunere accentul trebuie pus pe algoritmul (modulul) principal nu asupra subproblemelor.
La acest nivel nu ne interesează amănunte legate de rezolvarea subproblemelor, presupunem că le ştim
rezolva, eventual că avem deja scrişi SUBPROGRAMi pentru rezolvarea lor. Urmează să considerăm pe
rând fiecare subproblemă în parte şi să proiectăm (în acelaşi mod) un SUBPROGRAM pentru rezolvarea
ei. În final, se va descrie SUBPROGRAMul de rezolvare al fiecărei subprobleme, dar şi interacţiunile
dintre aceşti SUBPROGRAMi şi ordinea în care ei sunt folosiţi.
Noţiunea de modul va fi definită în secţiunea următoare. Deocamdată înţelegem prin modul orice
SUBPROGRAM sau algoritmul principal. Legătura dintre module se prezintă cel mai bine sub forma unei
diagrame numită arbore de programare. Fiecărui modul îi corespunde în arborele de programare un nod,
ai cărui descendenţi sunt toate modulele apelate direct. Nodul corespunzător algoritmului principal este
chiar nodul rădăcină.
În multe cărţi metoda top-down este întâlnită şi sub denumirea stepwise-refinement, adică
rafinare în paşi succesivi. Este vorba de un proces de detaliere pas cu pas a specificaţiei, denumit
proiectare descendentă. Algoritmul apare în diferite versiuni succesive, fiecare fiind o detaliere a versiunii
precedente.
Scopul urmărit este acelaşi: concentrarea atenţiei asupra părţilor importante ale momentului şi amânarea
detaliilor pentru mai târziu. Dacă ar fi necesar să le deosebim am spune că metoda top-down se referă la
nivelul macro iar metoda rafinării succesive la nivel micro. La nivel macro se doreşte descompunerea
unei probleme complexe în subprobleme. La nivel micro se doreşte obţinerea unui modul în versiune
finală. Într-o versiune intermediară pot fi prezente numai părţile importante ale acestuia, urmând să se
revină asupra detaliilor în versiunile următoare (aşa cum s-a arătat în secţiunea 1.5), după ce aspectele
importante au fost rezolvate.
Avantajele proiectării top-down (cunoscută şi sub denumirea "Divide et impera") sunt multiple.
Avantajul principal constă în faptul că ea permite programatorului să reducă complexitatea problemei,
subproblemele în care a fost descompusă fiind mai simple, şi să amâne detaliile pentru mai târziu. În
momentul în care descompunem problema în subprobleme nu ne gândim cum se vor rezolva
subproblemele ci care sunt ele şi conexiunile dintre ele.
23

22. Proiectarea descendentă permite lucrul în echipe mari. Prin descompunerea problemei în mai
multe subprobleme, fiecare subproblemă poate fi dată spre rezolvare unei subechipe. Fiecare subechipă
nu cunoaşte decât subproblema pe care trebuie să o rezolve.
Metoda "Divide et Impera" poate fi folosită nu numai la împărţirea problemei în subprobleme ci
şi la împărţirea datelor în grupe mai mici de date. Un astfel de procedeu este folosit de SUBPROGRAMul
Quicksort.
Metoda ascendentă (bottom-up) porneşte de la propoziţiile limbajului şi de la SUBPROGRAMi
existenţi, pe care îi asamblează în alţi SUBPROGRAMi pentru a ajunge în final la algoritmul dorit. Cu
alte cuvinte, în cazul metodei ascendente va fi scris mai întâi SUBPROGRAMul apelat şi apoi cel care
apelează. Ca rezultat al proiectării ascendente se ajunge la o mulţime de SUBPROGRAMi care se
apelează între ei. Este important să se cunoască care SUBPROGRAM apelează pe care, lucru redat printr-
o diagramă de structură, ca şi în cazul programării descendente.
Această metodă are marele dezavantaj că erorile de integrare vor fi detectate târziu, abia în faza de
integrare. Se poate ajunge abia acum la concluzia că unii SUBPROGRAMi, deşi corecţi, nu sunt utili.
De cele mai multe ori nu se practică o proiectare ascendentă sau descendentă pură ci o combinare
a lor, o proiectare mixtă.
3.3 Proiectarea modulară
Prin proiectare (programare) modulară înţelegem metoda de proiectare (programare) a unui
algoritm pentru rezolvarea unei probleme prin folosirea modulelor.
Dar ce este un modul? Modulul este considerat o unitate structurală de sine stătătoare, fie
program, fie subprogram, fie o unitate de program. Un modul poate conţine sau poate fi conţinut într-alt
modul. Un modul poate fi format din mai multe submodule. Astfel, în Pseudocod fiecare
SUBPROGRAM şi algoritmul principal sunt considerate module. În limbajele de programare cu structură
de bloc UNIT-urile pot fi considerate module. La compilarea separată un grup de subprograme compilate
deodată constituie un modul, dar acest modul poate fi considerat ca o mulţime de submodule din care este
compus.
Este însă important ca fiecare modul să-şi aibă rolul său bine precizat, să realizeze o funcţie în
cadrul întregului program. El apare în mod natural în descompunerea top-down.
Indiferent că privim modulul ca un singur SUBPROGRAM, un grup de SUBPROGRAMi, sau un
algoritm de sine stătător ce apelează alţi SUBPROGRAMi, considerăm modulele relativ independente,
dar cu posibilităţi de comunicare între ele. Astfel, un modul nu trebuie să fie influenţat de maniera în care
se lucrează în interiorul altui modul. Orice modificare ulterioară în structura unui program, dacă funcţia
pe care o realizează un modul M încă este necesară, acest modul trebuie să fie util şi folosit în continuare
fără modificări.
Rezultă că programarea modulară se bazează pe descompunerea problemei în subprobleme şi
proiectarea şi programarea separată a SUBPROGRAMilor corespunzători. De altfel, considerăm că într-o
programare serioasă nu se poate ajunge la implementare fără a avea în prealabil algoritmii descrişi într-un
limbaj de descriere (la noi Pseudocod). Deci programarea modulară se referă în primul rând la proiectarea
modulară a algoritmilor şi apoi la traducerea lor în limbajul de programare ales, ţinând seama de
specificul acestui limbaj. Programarea modulară este strâns legată de programarea ascendentă şi de
programarea descendentă, ambele presupunând folosirea SUBPROGRAMilor pentru toate subproblemele
întâlnite.
Avantajele programării modulare sunt multiple. Menţionăm în cele ce urmează câteva dintre ele.
Descompunerea unei probleme complexe în subprobleme este un mijloc convenabil şi eficient de a reduce
complexitatea (Principiul Divide et impera acţionează şi în programare). Este evident că
probabilitatea apariţiei erorilor în conceperea unui program creşte cu mărimea programului, lucru
confirmat şi de experienţa practică. De asemenea, rezolvând o problemă mai simplă, testarea unui modul
se poate face mult mai uşor decât testarea întregului algoritm.
24

23. Apoi, faptul că trebuiesc proiectate mai multe subprograme pentru subproblemele întâlnite,
permite munca mai multor programatori. S-a ajuns astfel la munca în echipă, modalitate prin care se
ajunge la scurtarea termenului de realizare a produsului program.
Modulele se pot refolosi ori de câte ori avem nevoie de ele. Astfel, s-a ajuns la compilarea
separată a subprogramelor şi la păstrarea subprogramelor obţinute în biblioteci de subprograme, de unde
ele se pot refolosi la nevoie. Sunt cunoscute astăzi multe astfel de biblioteci de subprograme.
Reutilizabilitatea acestor subprograme este o proprietate foarte importantă în activitatea de programare.
Ea duce la mărirea productivităţii în programare, dar şi la creşterea siguranţei în realizarea unui produs
corect.
Uneori, în timpul proiectării algoritmului sau a implementării lui, se ajunge la concluzia că
proiectarea a fost incompletă sau că unele module sunt ineficiente. şi în această situaţie programarea
modulară este avantajoasă, ea permiţând înlocuirea modulului în cauză cu altul mai performant.
Una din activităţile importante în realizarea unui program este verificarea corectitudinii acestuia.
Experienţa a arătat că modulele se pot verifica cu atât mai uşor cu cât sunt mai mici. Abilitatea omului de
a înţelege şi analiza corectitudinea unui SUBPROGRAM este mult mai mare pentru texte scurte. În unele
cărţi chiar se recomandă a nu se folosi SUBPROGRAMi mai mari decât 50 de propoziţii. Sigur că o astfel
de limită nu există, dar se recomandă descompunerea unui SUBPROGRAM în alţi SUBPROGRAMi
oricând acest lucru este posibil în mod natural, deci aceşti noi SUBPROGRAMi rezolvă subprobleme de
sine stătătoare, sau realizează funcţii bine definite.
3.4 Programarea structurată
Programarea structurată este un stil de programare apărut în urma experienţei primilor ani de
activitate. Ea cere respectarea unei discipline de programare şi folosirea riguroasă a câtorva structuri de
calcul. Ca rezultat se va ajunge la un algoritm uşor de urmărit, clar şi corect.
Termenul programare, folosit în titlul acestei secţiuni şi consacrat în literatura de specialitate, este
folosit aici în sens larg şi nu este identic cu cel de programare propriu-zisă. Este vorba de întreaga
activitate depusă pentru obţinerea unui program, deci atât proiectarea algoritmului cât şi traducerea
acestuia în limbajul de programare ales.
Bohm şi Jacopini au demonstrat că orice algoritm poate fi compus din numai trei structuri de
calcul:
– structura secvenţială;
– structura alternativă;
– structura repetitivă.
Fiecare din aceste structuri, ca parte dintr-o schemă logică, are o singură intrare şi o singură ieşire
şi sunt prezentate în figura 1.3.1.
Knuth consideră programarea structurată ca fiind un mijloc de a face produsele program mai uşor
de citit. De asemenea, programarea structurată este definită ca fiind programarea în care abordarea este
top-down, organizarea muncii este făcută pe principiul echipei programatorului şef, iar în proiectarea
algoritmilor se folosesc cele trei structuri de calcul definite de Bohm-Jacopini.
Alţi autori consideră programarea structurată nu ca o simplă metodă de programare ci ansamblul
tuturor metodelor de programare cunoscute. Dar programarea modulară, programarea top-down, sau
bottom-up (ascendentă sau descendentă) au apărut înaintea programării structurate. Important este faptul
că programarea structurată presupune o disciplină în activitatea de programare.
Considerăm că programarea structurată se poate întâlni:
– la nivel micro, privind elaborarea unui SUBPROGRAM;
– la nivel macro, privind dezvoltarea întregului produs informatic (algoritm).
La nivel micro programarea structurată este cea în care autorul este atent la structura fiecărui
modul în parte, cerând claritate şi ordine în scriere şi respectarea structurilor de calcul definite mai sus.
25

24. La nivel macro programarea structurată presupune practicarea proiectării top-down, a programării
modulare şi a celorlalte metode de programare, cerând ordine în întreaga activitate şi existenţa unei
structuri clare a întregii aplicaţii, precizată prin diagrama de structură a aplicaţiei.
În acest scop am definit limbajul Pseudocod, care are structurile de calcul menţionate. Schemele
logice obţinute dintr-o descriere în Pseudocod a unui algoritm, conform semanticii propoziţiilor
Pseudocod, se numesc D-scheme (de la Dijkstra) sau scheme logice structurate.
26

25. CAPITOLUL IV
ANALIZA ALGORITMILOR
O anumită problemă poate fi rezolvată cu ajutorul calculatorului numai dacă se găseşte un
algoritm pentru rezolvarea ei, care este dat calculatorului sub forma unui program. Întrucât toate
problemele practice pe care le întâlnim se pot rezolva cu ajutorul calculatorului, s-ar putea crede că orice
problemă este rezolvabilă. Această afirmaţie este însă falsă. Se ştie că nu există un program care să
rezolve "problema terminării programelor":
"Scrieţi un program care să decidă dacă un algoritm oarecare, dat, intră sau nu într-un ciclu infinit".
Chiar şi problemele pentru care există algoritmi corespunzători nu sunt neapărat rezolvabile cu
calculatorul. Este posibil ca timpul necesar execuţiei acestor algoritmi, sau cantitatea de memorie
necesară, să nu permită folosirea lor în practică.
Evident, dacă spaţiul de memorie necesar programului este mai mare decât cantitatea de memorie
disponibilă, programul nu poate fi executat. De asemenea, dacă numărul calculelor ce trebuie efectuat este
foarte mare, programul poate fi inutil. Iar asta se poate întâmpla destul de uşor în cazul problemelor ce
trebuiesc rezolvate în timp real (adică soluţia trebuie obţinută înaintea unui timp critic).
Iată câteva motive pentru care este necesar să analizăm algoritmii pe care-i concepem pentru
rezolvarea unei probleme.
Ne interesează să analizăm un program din mai multe puncte de vedere:
1) Corectitudine;
2) Eficienţă;
3) Posibilitate de îmbunătăţire;
4) Alte calităţi pe care le are.
4.1 Corectitudinea programelor
Un program este corect dacă el satisface specificaţiile problemei. Nu ne interesează câtă memorie
foloseşte acest program, din câte instrucţiuni este compus, sau cât timp de execuţie necesită. Cu alte
cuvinte, un program este corect dacă pentru acele date de intrare care satisfac specificaţiile problemei
rezultatele obţinute în urma execuţiei sunt corecte.
Pentru orice program P deosebim trei tipuri de variabile, pe care le vom grupa în trei vectori X, Y
şi Z. Componentele vectorului X desemnează variabilele de intrare, deci datele presupuse cunoscute în
problema rezolvată prin programul P. Componentele vectorului Z sunt variabilele care reprezintă
rezultatele cerute de problemă. În sfârşit, componentele vectorului Y sunt variabilele de lucru, care
notează diferitele rezultate intermediare necesare în program.
O problemă nu are sens pentru orice date de intrare. Vom folosi predicatul R(X) pentru a preciza
datele pentru care problema are sens. R(X) se numeşte predicat de intrare sau precondiţie. Pentru acele
valori ale lui X pentru care predicatul este adevărat problema are sens, pentru celelalte nu are sens să
executăm programul P.
Între rezultatele Z ale problemei şi datele iniţiale X (cunoscute în problemă) există anumite relaţii.
Vom reda aceste relaţii prin predicatul de ieşire R(X,Z), numit şi postcondiţie. Acesta este corect pentru
acele valori a şi b ale vectorilor X şi Z pentru care rezultatele problemei sunt b în cazul când datele iniţiale
sunt a şi este fals în caz contrar. Deci, dacă executând programul cu datele iniţiale a obţinem rezultatele
b' şi R(a,b') este fals, acest fapt este un indiciu că rezultatele obţinute în program nu sunt corecte. Apare o
altă regulă: fiecare variabilă să aibă semnificaţia ei şi să nu fie folosită în scopuri diferite.
27

26. 4.2 Testarea şi depanarea programelor
Testarea programelor este activitatea prin care programatorul observă comportarea programului
în urma execuţiei lui cu date de test. Evident, primul lucru urmărit este corectitudinea rezultatelor obţinute
în urma execuţiei programului cu datele de test folosite. Dar se va urmări şi dacă programul are alte
caracteristici ca: utilitate, siguranţă în funcţionare, robusteţe, performanţă. Este beneficiarul mulţumit de
rezultatele care se obţin şi de forma sub care sunt prezentate? Sunt ele obţinute în timp util?
Datele de test sunt date de intrare alese pentru variabilele de intrare pentru care se cunosc
rezultatele, sau avem unele informaţii despre rezultate. Executând programul cu aceste date ar trebui să
ajungem la rezultatele cunoscute.
Corectitudinea rezultatelor în aceste execuţii nu demonstrează corectitudinea programului în
general. Testarea însă pune adeseori în evidenţă erori făcute în diferite faze ale programării. În privinţa
aceasta dăm un citat din Dijkstra: Testarea programelor poate fi un mijloc eficient de a indica prezenţa
erorilor, dar din păcate, nu şi un mijloc de a demonstra absenţa lor.
Cu toate că ea nu demonstrează corectitudinea programului, testarea măreşte certitudinea
corectitudinii lui şi este deocamdată singura metodă practică de certificare a programului. Ar fi de dorit
demonstrarea apriori a corectitudinii programului, dar rezultatele cunoscute în prezent în această direcţie
nu sunt aplicabile programelor complexe.
Scopul testării programelor este depistarea şi eliminarea erorilor. Acest lucru este făcut prin
execuţia programului cu date de test pentru care se cunosc dinainte rezultatele (sau cel puţin se ştie ceva
despre ele) şi se observă rezultatele obţinute în urma execuţiei. În cazul în care rezultatele obţinute în
urma execuţiei nu sunt cele aşteptate se vor căuta şi elimina erorile. Activitatea care urmăreşte
descoperirea cauzelor erorilor şi înlăturarea lor se numeşte depanare.
Se pune problema alegerii datelor de test şi a numărului de execuţii ce trebuie făcute pentru a
putea considera că programul nu are erori. Numărul tuturor seturilor de date de intrare posibile este
teoretic infinit chiar şi pentru probleme simple. Deci nu poate fi vorba de o testare exhaustivă. Stabilirea
datelor de test se poate face cel puţin pe două căi:
– ţinând seama de specificaţia problemei;
– ţinând seama de textul programului.
Aşa cum va rezulta din cele ce urmează, cea mai bună cale este una mixtă, în care sunt combinate
aceste două posibilităţi.
La testarea după specificaţia problemei, stabilirea datelor de test se face analizând specificaţia
problemei. Se recomandă stabilirea datelor de test ţinând seama de specificaţia asupra datelor de intrare şi
de specificaţia asupra datelor de ieşire. Această metodă de testare este adecvată problemelor simple. În
cazul unei probleme complexe aplicarea ei este imposibilă datorită numărului foarte mare de cazuri
posibile, care ar trebui testate. Însă problema noastră a fost descompusă în subprobleme mai mici,
invizibile în specificaţie şi a căror testare este mai simplă. Privind programul ca o cutie neagră nu vom
mai ţine seama de aceste subprobleme. Totuşi, testarea după specificaţia problemei rămâne o metodă utilă
în testarea modulelor.
Testarea după textul programului ţine seama, pentru a stabili datele de test, de instrucţiunile
care trebuiesc executate. Considerând că algoritmul este descris printr-o schemă logică, o execuţie a
programului înseamnă parcurgerea unui drum de la START la STOP în această schemă. Dacă la această
execuţie rezultatele obţinute sunt corecte probabil că textul algoritmului pe acest drum este corect. Ar
trebui să verificăm toate blocurile schemei logice şi mai ales toate drumurile de la START la STOP
posibile. Cu observaţia că în cazul a două drumuri ce diferă doar prin faptul că o anumită buclă se execută
de n1, respectiv n2 ori le vom considera echivalente între ele. Dintre toate drumurile echivalente între ele
vom testa un singur drum, altfel am avea o infinitate de drumuri de testat.
În concluzie vom alege pentru fiecare drum un set de date de test, numărul execuţiilor fiind egal
cu numărul acestor drumuri. Dacă toate execuţiile au dat rezultate corecte programul se consideră testat.
Dacă însă la o singură execuţie am depistat erori, corectarea lor a modificat textul algoritmului şi testarea
trebuie reluată pe toate drumurile afectate de această schimbare.
28

27. Pentru un program complex, deci pentru o schemă logică cu un număr foarte mare de drumuri
START-STOP, testarea ar fi o activitate complexă, constând dintr-un număr foarte mare de execuţii. Încă
un motiv pentru a practica programarea modulară, caz în care testarea se face asupra unor module mai
mici şi asupra interfeţei dintre ele, aşa cum se va menţiona mai jos.
Stabilirea datelor de test după textul programului are şi unele dezavantaje. În primul rând,
programul poate fi incomplet şi să nu corespundă specificaţiilor. Pe drumurile existente el este corect, dar
lipsesc drumuri care, conform specificaţiilor, ar trebui să existe. Lipsa acestor drumuri este o greşeală
gravă care nu va fi descoperită de datele de test care ne duc doar pe drumurile existente. Din această
cauză se recomandă o testare mixtă.
În textul unui program există şi drumuri moarte, pe care nu se poate merge oricare ar fi datele de
intrare, deci nu putem găsi date de test corespunzătoare acestor drumuri. Adeseori aceste drumuri scot în
evidenţă erori prin simpla analiză a textului. Astfel, în succesiunea de propoziţii Pseudocod
DACĂ n<2 ATUNCI
. . .
DACĂ n>3 ATUNCI A SFDACĂ
. . .
SFDACĂ
grupul A este inaccesibil oricare ar fi valoarea lui n. Este însă foarte frecventă eroarea de omisiune a unui
caracter; în cazul nostru tastarea numărului 2 în loc de 20, ceea ce schimbă complet sensul textului
Pseudocod de mai sus.
Adesea este imposibil să se execute programul cu toate datele de test stabilite. În acest caz apare
problema alegerii acelei submulţimi din aceste date care să aibă şansa maximă de a depista erorile
prezente în program. Testarea minimă care trebuie făcută constă într-un număr de execuţii a programului
care să ne asigure că fiecare instrucţiune din program a fost executată cel puţin odată. Ea înseamnă mult
mai puţine execuţii decât toate drumurile START-STOP.
Există date de test care ne duc pe un anumit drum fără a depista erori existente în instrucţiunile
întâlnite şi alte date de test care depistează aceste erori. Încă un motiv pentru care se recomandă o testare
mixtă.
Ca ordine de folosire a datelor de test în timpul testării, se recomandă mai întâi testarea după
specificaţii şi apoi testarea după textul programului.
Este necesară şi testarea robusteţei programului, care înseamnă buna lui comportare la date de
intrare intenţionat greşite, pentru care problema nu are sens. Unele programe intră în aceste condiţii în
ciclu infinit, altele se termină cu erori de execuţie. Un program robust nu trebuie să fie afectat de datele de
intrare eronate. Comportarea cea mai normală în astfel de situaţii ar fi semnalarea unor mesaje de eroare
corespunzătoare.
La un produs program complex testarea este o activitate mult mai complicată. Este necesară o
testare separată a fiecărui modul în parte, o testare a interfeţei dintre module şi o testare a produsului în
ansamblu (testarea de integrare).
Testarea de integrare se referă la funcţionarea programului realizat în ansamblu. După ce fiecare
modul în parte a fost testat şi corectat, deci în ipoteza că fiecare modul în parte este corect, e necesar să se
verifice comportarea globală a programului. În această etapă găsirea erorilor, înlăturarea cauzelor care le-
a generat şi corectarea lor, poate fi
foarte dificilă, mai ales atunci când ele provin dintr-o proiectare greşită.
Execuţia unui program se poate termina anormal datorită apariţiei unor erori ca:
– împărţiri la zero;
– alte erori ce provoacă depăşiri;
– neconcordanţa între parametri actuali şi formali;
– depăşirea dimensiunii tablourilor.
Dar chiar şi la execuţia normală a programului putem avea erori, unele foarte grave, obţinând
rezultate greşite. În ambele situaţii urmează depanarea programului, adică descoperirea cauzei erorilor
şi înlăturarea lor.
29

28. O metodă utilă în depanarea programelor, în special pentru începători, este inserarea în program a
unor tipăriri auxiliare. Mai ales în locurile vecine cu instrucţiunile care au provocat eroarea şi pentru
variabilele implicate în producerea ei. Observarea valorilor unei variabile, a schimbărilor făcute în timpul
execuţiei, pot dezvălui programatorului cauza erorii. Cu siguranţă îi va arăta că o anumită variabilă ia alte
valori decât cele la care se aşteaptă el. De altfel, pe timpul testării unui program, sunt utile semnalările
oricăror semne de eroare. Recomandăm verificarea valorilor variabilelor imediat după obţinerea
acestora.
4.3 Complexitatea algoritmilor
În această secţiune ne va interesa eficienţa unui algoritm. Mai exact, ne interesează să comparăm
între ei mai mulţi algoritmi care rezolvă aceeaşi problemă. Care dintre ei este mai bun? Evident, vom
compara numai algoritmi despre care ştim că sunt corecţi.
Putem compara doi algoritmi în raport cu:
– cantitatea de memorie necesară;
– viteza de lucru, deci timpul necesar rezolvării problemei.
Dacă în urmă cu două decenii volumul de memorie necesar rezolvării unei probleme era un factor
important din cauza memoriei reduse existente la calculatoarele din acel timp, astăzi acest factor a devenit
mai puţin important. Calculatoarele actuale au memorie suficient de mare pentru marea majoritate a
algoritmilor întâlniţi.
Timpul necesar execuţiei unui program depinde de numărul operaţiilor ce trebuiesc executate. Iar
numărul operaţiilor efectuate depinde de datele de intrare, deci se schimbă de la o execuţie la alta.
Există însă un cel mai rău caz, pentru acele date de intrare pentru care numărul operaţiilor
efectuate este maxim. În acest caz vorbim de complexitate în cel mai rău caz.
De asemenea, putem vorbi de numărul mediu de operaţii efectuate într-o execuţie. Dacă numărul
execuţiilor posibile este finit atunci acest număr mediu este egal cu numărul operaţiilor efectuate în toate
execuţiile, împărţit la numărul execuţiilor. Sunt însă foarte puţine programe cu această proprietate. Pentru
aproape toate programele, cel puţin teoretic, numărul execuţiilor posibile este infinit.
4.4 Documentarea programelor
În paralel cu elaborarea programului trebuie elaborată şi o documentaţie. Aceasta va conţine toate
deciziile luate în crearea programului. Documentarea este activitatea de prezentare a programului celor
care vor fi interesaţi să obţină informaţii despre el. Aceştia sunt în primul rând persoanele care au realizat
programul, apoi persoanele care-l vor folosi şi persoanele solicitate să facă întreţinerea acestuia.
Adeseori se întâlnesc programe fără nici o altă documentaţie în afara textului propriu-zis al
programului. În graba de a termina cât mai repede, programul nu este însoţit de nici o documentaţie şi
frecvent nu sunt folosite nici comentarii în textul programului.
Sigur că însăşi textul programului constituie o autodocumentare. Iar comentariile prezente în
program dau explicaţii suplimentare despre program. Este însă necesară o documentaţie completă, scrisă,
care va conţine:
– enunţul iniţial al problemei;
– specificaţia (vezi secţiunea 4.1);
– documentaţia de proiectare (metoda de rezolvare aleasă şi proiectarea algoritmilor
folosiţi. Pentru fiecare algoritm va fi prezentată subproblema corespunzătoare, cu
specificaţia ei şi rolul fiecărei variabile);
– documentaţia de programare, care va include textul programului;
– datele de test folosite;
– documentaţie privind exploatarea programului;
– modificări făcute în timpul întreţinerii programului.
30

29. Menţionăm că cele mai recente produse realizate de firmele consacrate au, pe lângă documentaţia
scrisă, şi o autodocumentaţie (funcţii HELP).
Referitor la autodocumentare, folosirea comentariilor, alegerea cu grijă a denumirii
variabilelor, cât şi claritatea textului, obţinută prin indentare şi grijă asupra structurii
programului, este utilă nu numai pe timpul elaborării programului, dar mai ales pe timpul întreţinerii şi
modificărilor ulterioare.
Denumirea variabilei să fie astfel aleasă încât să redea cât mai bine semnificaţia ei.
Cei care au dorit să refolosească programe scrise cu câteva luni în urmă înţeleg foarte bine
diferenţa dintre un program însoţit de comentarii explicative şi un program fără nici o explicaţie. Uitarea
acţionează asupra oricărei persoane şi, chiar dacă este posibilă, descifrarea unui program cere timp şi nu
este o sarcină prea uşoară. Comentariile sunt recomandate, fiind un mijloc de autodocumentare a
programului sursă.
Sigur că prima documentaţie a oricărui program este textul sursă propriu-zis. Este bine ca acest
text să poată fi citit cât mai uşor, iar programarea structurată duce la un program mai uşor de citit decât
unul lipsit de orice structură.
Este însă nevoie şi de o documentaţie însoţitoare scrisă, care constituie documentarea propriu-zisă
a programului. Aceasta trebuie să redea toate deciziile făcute în timpul proiectării, să prezinte diagrama
de structură a întregului produs şi fiecare parte separat. Pentru fiecare modul documentaţia va conţine:
– numele acestuia;
– datele de intrare;
– datele de ieşire;
– funcţia realizată de modulul respectiv;
– variabilele folosite şi semnificaţia lor;
– algoritmul propriu-zis.
Este necesar ca aceste informaţii să se afle şi sub forma unor comentarii în textul programului. De
asemenea, documentaţia va conţine şi textul final al programului.
Este necesară şi o documentaţie de folosire a produsului realizat. Beneficiarul nu este interesat de
modul în care a fost realizat programul ci de modul în care îl poate folosi.
O documentare completă a unui program poate fi utilă nu numai pentru folosirea şi întreţinerea
programului. Componente ale unui produs existent pot fi utile şi în realizarea altor produse. Este însă
necesar să se înţeleagă cât mai uşor ce funcţii realizează aceste componente şi cu ce performanţe.
Folosirea acestor componente existente, testate şi documentate, duce evident la creşterea productivităţii în
realizarea noului produs.
4.5 Stil în programare
Fiecare programator are stilul să propriu de concepere şi redactare a unui program. Este bine ca el
să respecte anumite reguli generale de programare, astfel încât programele elaborate să aibă anumite
calităţi.
Calităţile pe care le poate avea un program sunt următoarele:
Corectitudine = proprietatea programului de a respecta specificaţiile şi a da rezultate corecte;
Extensibilitate = posibilitatea adaptării programului la unele schimbări în specificaţie;
Robusteţe = abilitatea de a recunoaşte situaţiile în care problema ce se rezolvă nu are sens şi de a se
comporta în consecinţă (de exemplu, prin mesaje de eroare corespunzătoare);
Reutilizabilitate = posibilitatea reutilizării întregului program sau a unor părţi din el în alte aplicaţii;
Compatibilitate = uşurinţa de combinare cu alte produse program;
Portabilitate = posibilitatea de folosire a produsului program pe alte sisteme de calcul, diferite de cel pe
care a fost conceput;
Eficienţă = măsura în care sunt bine folosite resursele sistemului de calcul;
Claritate = uşurinţa citirii şi înţelegerii textului programului, a structurilor din care este compus şi a
rolului denumirilor şi părţilor sale.
31

30. Un produs program este considerat de calitate dacă are calităţile de mai sus, dacă lansat în
execuţie dă rezultate corecte, dacă textul lui se poate citi şi înţelege, dacă poate fi uşor întreţinut şi dacă
este terminat la data fixată.
Stilul unui programator este dat de măsura în care programul său are aceste calităţi şi de
vizibilitatea lor. Evident, pe lângă aceste calităţi, vizibile şi în text, stilul de programare este dat şi de
corectitudinea şi robusteţea produselor realizate. Programul trebuie să funcţioneze şi la introducerea unor
date greşite (pentru care problema nu are sens), recunoscând această situaţie şi semnalând-o. În acelaşi
timp rezultatele obţinute pentru date pentru care problema are sens trebuie să fie corecte. Iar
corectitudinea sau incorectitudinea programului este o consecinţă a modului în care programatorul a
respectat regulile de programare (vezi capitolul 8) şi a experienţei obţinute în activitatea de programare.
Privind claritatea algoritmului trebuie să observăm că indentarea (paragrafarea) este un alt mijloc
de a mări claritatea scrierii. Textul unui algoritm poate fi scris cuvânt după cuvânt, completând tot rândul
asemeni textului unui roman. Claritatea lui este mică, după cum urmează:
PROGRAMUL CLASAMENT ESTE:
DATE m,n,NUMEi, i=1,n, NOTEi,j, j=1,m, i=1,n;
PENTRU i:=1,n EXECUTĂ {calculează media generală a elevului i}
FIE S:=0;
PENTRU j:=1,m EXECUTĂ S:=S+NOTEi,j SFPENTRU
FIE MEDIIi:=S/M
SFPENTRU
PENTRU j:=1,m EXECUTĂ
CHEAMĂ ORDINE(n,NOTEj,O);
CHEAMĂ TIPAR(n, NUME, O)
SFPENTRU
CHEAMĂ ORDINE(n,MEDII,O);
CHEAMĂ TIPAR(n,NUME,O)
SFALGORITM
Considerăm că fiecare programator trebuie să respecte anumite reguli de scriere a programelor, cu
gândul la claritatea textului. În unele cărţi sunt date mai multe reguli de indentare. Astfel, Gries sugerează
următoarele reguli:
- instrucţiunile unei secvenţe se vor scrie aliniate, începând toate în aceeaşi coloană;
- instrucţiunile unei structuri de calcul (instrucţiuni compuse) se vor scrie începând toate
din aceeaşi coloană, aflată cu 2-4 caractere la dreapta faţă de începutul instrucţiunii
compuse;
- pe o linie pot fi scrise mai multe instrucţiuni, cu condiţia ca ele să aibă ceva comun.
Astfel, 2-4 instrucţiuni scurte de atribuire pot fi scrise pe acelaşi rând. Acest lucru se
recomandă în vederea unei scrieri compacte a programului. E bine ca un program ce se
poate scrie pe o pagină, cu respectarea structurii lui, să nu fie întins pe două pagini !
Considerăm că nu există reguli de scriere obligatorii pentru toată lumea! Dar fiecare programator
trebuie să aibă propriile lui reguli de scriere.
Tot privind claritatea scrierii programului, se recomandă ca denumirile variabilelor să fie astfel
alese încât să reflecte semnificaţia acestor variabile.
Un alt mijloc de a mări claritatea textului unui program constă în inserarea comentariilor în text.
Comentariile sunt texte explicative închise între acolade. Ele au rolul de a explica cititorului anumite
părţi din program. Am spus deja că în proiectarea algoritmilor folosim şi propoziţii nestandard care vor fi
pe parcurs înlocuite cu propoziţii standard. E bine ca aceste propoziţii să rămână în text sub formă de
comentarii.
Comentariile vor fi prezente:
– în capul programului, pentru a prezenta titlul şi scopul programului, perioada realizării
lui şi numele programatorului;
32

31. – în definiţii, pentru a descrie semnificaţia notaţiilor folosite (a variabilelor, constantelor,
SUBPROGRAMilor etc);
– în dreapta unor instrucţiuni, pentru a descrie rolul acestora, sau cazul în care se atinge
acea instrucţiune;
– între părţile unui modul mai lung, pentru a explica rolul fiecărei părţi.
Sperăm că prin exemplele date în acest material am prezentat un stil propriu de programare şi am
convins cititorul de necesitatea formării propriului său stil.
33

32. CAPITOLUL V
CLASE DE ALGORITMI
Căutarea şi Sortarea sunt două dintre cele mai des întâlnite subprobleme în programare. Ele
constituie o parte esenţială din numeroasele procese de prelucrare a datelor. Operaţiile de căutare şi
sortare sunt executate frecvent de către oameni în viaţa de zi cu zi, ca de exemplu căutarea unui cuvânt în
dicţionar sau căutarea unui număr în cartea de telefon.
Căutarea este mult simplificată dacă datele în care efectuăm această operaţie sunt sortate
(ordonate, aranjate) într-o anumită ordine (cuvintele în ordine alfabetică, numerele în ordine crescătoare
sau descrescătoare).
Sortarea datelor constă în rearanjarea colecţiei de date astfel încât un câmp al elementelor
colecţiei să respecte o anumită ordine. De exemplu în cartea de telefon fiecare element (abonat) are un
câmp de nume, unul de adresă şi unul pentru numărul de telefon. Colecţia aceasta respectă ordinea
alfabetică după câmpul de nume.
Dacă datele pe care dorim să le ordonăm, adică să le sortăm, sunt în memoria internă, atunci
procesul de rearanjare a colecţiei îl vom numi sortare internă, iar dacă datele se află într-un fişier
(colecţie de date de acelaşi fel aflate pe suport extern), atunci procesul îl vom numi sortare externă.
Fiecare element al colecţiei de date se numeşte articol iar acesta la rândul său este compus din
unul sau mai multe componente. O cheie C este asociată fiecărui articol şi este de obicei unul dintre
componente. Spunem că o colecţie de n articole este ordonat crescător după cheia C dacă C(i) ≤ C(j)
pentru 1≤i<j≤n, iar dacă C(i) ≥ C(j) atunci şirul este ordonat descrescător.
5.1 Algoritmi de căutare
În acest subcapitol vom studia câteva tehnici elementare de căutare şi vom presupune că datele se
află în memoria internă, într-un şir de articole. Vom căuta un articol după un câmp al acestuia pe care îl
vom considera cheie de căutare. În urma procesului de căutare va rezulta poziţia elementului căutat (dacă
acesta există).
Notând cu k1, k2, ...., kn cheile corespunzătoare articolelor şi cu a cheia pe care o căutăm, problema
revine la a găsi (dacă există) poziţia p cu proprietatea a = kp.
De obicei articolele sunt păstrate în ordinea crescătoare a cheilor, deci vom presupune că
k1 < k2 < .... < kn .
Uneori este util să aflăm nu numai dacă există un articol cu cheia dorită ci şi să găsim în caz contrar locul
în care ar trebui inserat un nou articol având cheia specificată, astfel încât să se păstreze ordinea existentă.
Deci problema căutării are următoarea specificare:
Date a,n,(ki, i=1,n);
Precondiţia: n∈N, n≥1 şi k1 < k2 < .... < kn ;
Rezultate p;
Postcondiţia: (p=1 şi a ≤ k1) sau (p=n+1 şi a > kn) sau (1<p≤n) şi (kp-1 < a ≤ kp).
Pentru rezolvarea acestei probleme vom descrie mai mulţi SUBPROGRAMi.
O primă metodă este căutarea secvenţială, în care sunt examinate succesiv toate cheile.
SUBPROGRAMul CautSecv(a,n,K,p) este: {n∈N, n≥1 şi}
{k1 < k2 < .... < kn}
{Se caută p astfel ca:}
{(p=1 şi a ≤ k1) sau (p=n+1 şi a>kn)}
{sau (1<p≤n) şi (kp-1 < a ≤ kp)}
Fie p:=0; {Cazul "încă negasit"}
34

33. Dacă a≤k1 atunci p:=1 altfel
Dacă a>kn atunci p:=n+1 altfel
Pentru i:=2; n execută
Dacă (p=0) şi (a≤ki) atunci p:=i sfdacă
sfpentru
sfdacă
sfdacă
sf-CautSecv
Se observă că prin această metodă se vor executa în cel mai nefavorabil caz n-1 comparări,
întrucât contorul i va lua toate valorile de la 2 la n. Cele n chei împart axa reală în n+1 intervale. Tot
atâtea comparări se vor efectua în n-1 din cele n+1 intervale în care se poate afla cheia căutată, deci
complexitatea medie are acelaşi ordin de mărime ca şi complexitatea în cel mai rău caz.
Evident că în multe situaţii acest algoritm face calcule inutile. Atunci când a fost deja găsită cheia
dorită este inutil a parcurge ciclul pentru celelalte valori ale lui i. Cu alte cuvinte este posibil să înlocuim
ciclul PENTRU cu un ciclu CÂTTIMP. Ajungem la un al doilea algoritm, dat în continuare.
SUBPROGRAMul CautSucc(a,n,K,p) este: {n∈N, n≥1 şi}
{k1 < k2 < .... < kn}
{Se caută p astfel ca:}
{(p=1 şi a ≤ k1) sau (p=n+1 şi a>kn)}
{sau (1<p≤n) şi (kp-1 < a ≤ kp).
Fie p:=1;
Dacă a>k1 atunci
Câttimp p≤n şi a>kp executş p:=p+1 sfcât
sfdacă
sf-CautSecv
O altă metodă, numită căutare binară, care este mult mai eficientă, utilizează tehnica "divide et
impera" privitor la date. Se determină în ce relaţie se află cheia articolului aflat în mijlocul colecţiei cu
cheia de căutare. În urma acestei verificări căutarea se continuă doar într-o jumătate a colecţiei. În acest
mod, prin înjumătăţiri succesive se micşorează volumul colecţiei rămase pentru căutare. Căutarea binară
se poate realiza practic prin apelul funcţiei BinarySearch(a,n,K,1,n), descrisă mai jos, folosită în
SUBPROGRAMul dat în continuare.
SUBPROGRAMul CautBin(a,n,K,p) este: {n∈N, n≥1 şi k1 < k2 < .... < kn}
{Se caută p astfel ca: (p=1 şi a ≤ k1) sau}
{(p=n+1 şi a>kn) sau (1<p≤n) şi (kp-1 < a ≤ kp)}
Dacă a≤k1 atunci p:=1 altfel
Dacă a>kn atunci p:=n+1 altfel
p:=BinarySearch(a,n,K,1,n)
sfdacă
sfdacă
sf-CautBin
Funcţia BinarySearch (a,n,K,St,Dr) este:
Dacă St≥Dr-1
atunci BinarySearch:=Dr
altfel m:=(St+Dr) Div 2;
Dacă a≤K[m]
atunci BinarySearch:=BinarySearch(a,n,K,St,m)
altfel BinarySearch:=BinarySearch(a,n,K,m,Dr)
sfdacă
35

34. sfdacă
sf-BinarySearch
În funcţia BinarySearch descrisă mai sus, variabilele St şi Dr reprezintă capetele intervalului de
căutare, iar m reprezintă mijlocul acestui interval.
Se observă că funcţia BinarySearch se apelează recursiv. Se poate înlătura uşor recursivitatea, aşa
cum se poate vedea în următoarea funcţie:
Funcţia BinSeaNerec (a,n,K,St,Dr) este:
Câttimp Dr-St>1 execută
m:=(St+Dr) Div 2;
Dacă a≤K[m]
atunci Dr:=m
altfel St:=m
sfdacă
sfcât
BinSeaNerec:=Dr
sf-BinSeaNerec
5.2 Sortare internă
Prin sortare internă vom înţelege o rearanjare a unei colecţii aflate în memoria internă astfel
încât cheile articolelor să fie ordonate crescător (eventual descrescător).
Din punct de vedere al complexităţii algoritmilor problema revine la ordonarea cheilor. Deci
specificarea problemei de sortare internă este următoarea:
Date n,K; {K=(k1,k2,...,kn)}
Precondiţia: ki∈R, i=1,n
Rezultate K';
Postcondiţia: K' este o permutare a lui K, dar ordonată crescător.
Deci k1 ≤ k2 ≤ ... ≤ kn.
O primă tehnică numită "Selecţie" se bazează pe următoarea idee: se determină poziţia
elementului cu cheie de valoare minimă (respectiv maximă), după care acesta se va interschimba cu
primul element. Acest procedeu se repetă pentru subcolecţia rămasă, până când mai rămâne doar
elementul maxim.
SUBPROGRAMul Selectie(n,K) este: {Se face o permutare a celor}
{n componente ale vectorului K astfel}
{ca k1 ≤ k2 ≤ .... ≤ kn }
Pentru i:=1; n-1 execută
Fie ind:=i;
Pentru j:=i+1; n execută
Dacă kj < kind atunci ind:=j sfdacă
sfpentru
Dacă i<ind atunci t:=ki; ki:=kind; kind:=t sfdacă
sfpentru
sf-Selectie
Se observă că numărul de comparări este:
(n-1)+(n-2)+...+2+1=n(n-1)/2
indiferent de natura datelor.
A treia metodă care va fi prezentată, numită "BubbleSort", compară două câte două elemente
consecutive iar în cazul în care acestea nu se află în relaţia dorită, ele vor fi interschimbate. Procesul de
comparare se va încheia în momentul în care toate perechile de elemente consecutive sunt în relaţia de
ordine dorită.
36

35. SUBPROGRAMul BubbleSort (n,K) este:
Repetă
Fie kod:=0; {Ipoteza "este ordine"}
Pentru i:=2; n execută
Dacă ki-1 > ki atunci
t := ki-1;
ki-1 := ki;
ki:=t;
kod:=1 {N-a fost ordine!}
sfdacă
sfpentru
pânăcând kod=0 sfrep {Ordonare}
sf-BubbleSort
O metodă mai performantă de ordonare, care va fi prezentată în continuare, se numeşte
"QuickSort" şi se bazează pe tehnica "divide et impera" după cum se poate observa în continuare. Metoda
este prezentată sub forma unei proceduri care realizează ordonarea unui subşir precizat prin limita
inferioară şi limita superioară a indicilor acestuia. Apelul procedurii pentru ordonarea întregului şir este :
QuickSort(n,K,1,n), unde n reprezintă numărul de articole ale colecţiei date.
SUBPROGRAMul SortareRapidă (n,K) este:
Cheamă QuickSort(n,K,1,n)
sf-SortareRapidă
Procedura QuickSort (n,K,St,Dr) va realiza ordonarea subşirului kSt,kSt+1,..., kDr. Acest subşir va fi
rearanjat astfel încât kSt să ocupe poziţia lui finală (când şirul este ordonat). Dacă i este această poziţie,
şirul va fi rearanjat astfel încât următoarea condiţie să fie îndeplinită:
kj ≤ ki ≤ kl , pentru st ≤ j < i < l ≤dr (*)
Odată realizat acest lucru, în continuare va trebui doar să ordonăm subşirul kSt , kSt+1 , ... ,ki-1 prin
apelul recursiv al procedurii QuickSort(n,K,St,i-1) şi apoi subşirul ki+1,..., kDr prin apelul
QuickSort(i+1,Dr). Desigur ordonarea acestor două subşiruri (prin apelul recursiv al procedurii) mai este
necesară doar dacă acestea conţin cel puţin două elemente.
Procedura QuickSort este prezentată în continuare :
SUBPROGRAMul QuickSort (n,K,St,Dr) este:
Fie i:=St; j:=Dr; a:=ki;
Repetă
Câttimp kj >= a şi (i<j) execută j:=j-1 sfcât
ki:= kj;
Câttimp ki ≤ a şi (i<j) execută i:=i+1 sfcât
kj:= ki ;
pânăcând i=j sfrep
Fie ki := a;
Dacă St < i- 1 atunci Cheamă QuickSort(n,K,St,i-1) sfdacă
Dacă i+1 < Dr atunci Cheamă QuickSort(n,K,i+1,Dr) sfdacă
sf-QuickSort
Un ultim algoritm care va fi prezentat se numeşte "Merge Sort" (sortare prin interclasare) şi se
bazează pe tehnica "divide et impera". Şirul ce urmează a fi ordonat se împarte în două subşiruri care se
ordonează, după care acestea se vor interclasa obţinându-se întregul şir ordonat. Fiecare subşir se va
ordona tot prin despărţirea lui în două subşiruri urmată de interclasare şi aşa mai departe până când
37

36. ordonarea unui subşir se poate rezolva elementar fără a mai fi necesară despărţirea lui în alte două
subşiruri (lungimea subşirului este cel mult 2).
Algoritmul corespunzător este prezentat în secţiunea următoare sub forma unei proceduri
recursive care ordonează un subşir precizând limitele acestuia.
5.3 Interclasare
Fiind date două colecţii de date, ordonate crescător (sau descrescător) după o cheie, se cere să se
obţină o colecţie care să fie de asemenea ordonată crescător (respectiv descrescător) după aceeaşi cheie şi
care să fie formată din articolele colecţiilor date. Acest lucru se poate obţine direct (fără o sortare a
colecţiei finale) prin parcurgerea secvenţială a celor două colecţii, simultan cu generarea colecţiei cerute.
Prin compararea a două elemente din listele de intrare se va decide care element va fi adăugat în lista de
ieşire.
Deci ne interesează un algoritm de rezolvare a problemei ce are următoarea specificare:
Date m, (xi, i=1,m), n, (yi, i=1,n);
Precondiţia: {x1 ≤ x2 ≤ ... ≤ xm} şi {y1 ≤ y2 ≤ ... ≤ yn}
Rezultate k, (zi, i=1,k);
Postcondiţia: {k=m+n} şi {z1≤ z2≤ ...≤ zk} şi (z1,z2,..., zk) este o permutare a valorilor
(x1, ..., xm,y1,..., yn)
O soluţie posibilă ar fi depunerea componentelor vectorului X şi a componentelor vectorului Y în
vectorul Z, realizând astfel a doua parte din postcondiţie. Ordonând apoi componentele vectorului Z
obţinem soluţia dorită. Acest algoritm, deşi corect, este ineficient şi, în plus, nu este util în sortările
externe (vezi secţiunea 5.4). Este important ca la o singură trecere prin vectorii X şi Y să se obţină
vectorul Z. Acest lucru este realizat de următorul algoritm de interclasare:
SUBPROGRAMul Interclasare(m,X,n,Y,k,Z) este: {X are cele m}
{componente ordonate nedescrescător}
{La fel Y cu n componente. Cele m+n valori}
{se depun în Z, tot ordonate nedescrescător}
Fie i:=1; j:=1; k:=0;
Câttimp (i<=m) şi (j<=n) execută {Există componente}
Dacă xi≤yj
atunci Cheamă PUNE(i,xi,k,Z) {şi în X}
altfel Cheamă PUNE(j,yj,k,Z) {şi în Y}
sfdacă
sfcât
Câttimp (i<=m) execută {Există componente}
Cheamă PUNE(i,xi,k,Z) {numai în X}
sfcât
Câttimp (j<=n) execută {Există componente}
Cheamă PUNE(j,yj,k,Z) {numai în Y}
sfcât
sf-Interclasare
Aici s-a folosit SUBPROGRAMul PUNE(ind,val,k,Z) care pune în vectorul Z valoarea val şi
măreşte indicele ind cu 1, subalgortim dat în continuare.
SUBPROGRAMul PUNE(ind,val,k,Z) este: {Adaugă val}
k:=k+1; {în vectorul Z cu}
zk:=val; {k componente şi}
ind:=ind+1 {măreşte ind cu 1}
sf-PUNE
38

37. Algoritmul MergeSort de sortare bazat pe interclasare se poate vedea în continuare.
Algoritmul MergeSort este: {Sortare prin interclasare}
Citeşte n;
Pentru i:=1 ; n execută Citeşte Ki sfpentru
Cheamă SortInter (n,K);
Pentru i:=1; n execută Tipăreşte Ki sfpentru
sf-MergeSort
SUBPROGRAMul SortInter(n, C) este:
Cheamă Ordon (1,n,C);
sf-SortInter
SUBPROGRAMul Ordon (St,Dr,A) este: {Sortare prin interclasare a}
{elementelor ASt,ASt+1,...,ADr}
Dacă St < Dr atunci
Fie m:=(St+Dr) Div 2;
Cheamă Ordon (St,m,A);
Cheamă Ordon (m+1,Dr,A);
Cheamă Inter (St,m, m+1,Dr);
sfdacă
sf-Ordon
SUBPROGRAMul Inter (s1,d1, s2,d2) este: { Interclasare }
Fie A:=C; k:=s1-1;
Câttimp (s1<=d1) şi (s2<=d2) execută
Dacă (C[s1]<C[s2])
atunci Cheamă PUNE(s1,cs1 ,k,A)
altfel Cheamă PUNE(s2,cs2 ,k,A)
sfdacă
sfcât
Câttimp (s1<=d1) execută Cheamă PUNE(s1,cs1 ,k,A) sfcât
Câttimp (s2<=d2) execută Cheamă PUNE(s2,cs2 ,k,A) sfcât
C:=A
sf-Inter
5.4 Sortare externă
O problemă cu care ne confruntăm adesea este sortarea unei colecţii de date aflate pe un suport
extern, de volum relativ mare faţă de memoria internă disponibilă. În această secţiune o astfel de colecţie
de date o vom numi fişier. În acest caz nu este posibil transferul întregii colecţii în memoria internă
pentru a fi ordonată şi apoi din nou transferul pe suport extern. Dacă datele ce urmează a fi sortate ocupă
un volum de n ori mai mare decât spaţiul de memorie internă de care dispunem, atunci colecţia se va
împărţi în n subcolecţii ce vor fi transferate succesiv în memoria internă, se vor sorta pe rând şi vor fi
stocate din nou pe suportul extern sortate. Din acest moment prin operaţii de interclasare două câte două
se pot obţine colecţii de dimensiuni superioare până se obţine toată colecţia ordonată.
La aceste interclasări, pentru a efectua un număr cât mai mic de operaţii de transfer se recomandă
interclasarea colecţiilor de dimensiuni minime, apoi din datele obţinute din nou vor fi alese două colecţii
de dimensiuni minime şi aşa mai departe până se obţine o singură colecţie care va fi colecţia cerută, adică
sortată.
După metodele de sortare externă folosite, se descriu trei procedee de sortare externă:
39

38. – sortarea echilibrată;
– sortarea polifazică;
– sortarea în cascadă.
Evident că sortarea depinde şi de configuraţia calculatorului folosit, dar şi de suportul pe care se
află fişierul de sortat şi fişierele intermediare create.
Principial sortarea externă presupune parcurgerea a două etape importante:
a) Divizarea fişierului de sortat F, în n fişiere H1, H2, ..., Hn, cu sortarea internă a acestora;
b) Interclasarea acestor fişiere sortate pentru a ajunge la fişierul dorit G.
40

39. CAPITOLUL VI
EVOLUŢIA LIMBAJELOR DE PROGRAMARE
Un limbaj de programare este un sistem de convenţii adoptate pentru realizarea unei comunicări –
între programator şi calculator . Limbajele folosite pentru programarea unui calculator sunt extrem de
asemănătoare limbajelor naturale . Ele sunt compuse din :
 cuvinte (rezervate);
 punctuaţie;
 propoziţii şi fraze;
 reguli sintactice etc.
Aşa cum pentru însuşirea unei limbi străine trebuie învăţate cuvintele acesteia şi regulile cu care
pot fi manevrate tot aşa pentru însuşirea unui limbaj de programare trebuie studiate cuvintele şi semnele
care îl compun împreună împreună cu regulile de manevrare a lor.
De-a lungul timpului,oamenii au inventat masini pentru a calcula cat mai eficient.Inaintea
calculatoarelor performante din zilele noastre,au existat alte masini de calcul.
Momentul iniţial al istoriei calculatoarelor este, de obicei legat de numele matematicianului
englez Charles Babbage. El a propus în anul 1830 o Maşină Analitică care a anticipat în mod fascinant
structura calculatoarelor actuale. Ideile sale au devansat cu peste 100 de ani posibilităţiile tehnologice ale
vremii sale. Înaintea a mai fost încercări în acest domeniu ale lui Leibnitz şi Pascal (sec al XVII-lea) .
Următorul moment de referinţă este anul 1937, când Howard Aiken, de la Universitatea Harvard a
propus Calculatorul cu secvenţă de Comandă Automată, bazat pe o combinaţie între ideile lui Babbage şi
calculatoarele elertromecanice, produse de firma IBM. Construcţia acestuia a început în anul 1939 şi s-a
terminat în anul 1944, fiind denumit Mark I . El a fost în principal primul calculator electromecanic, fiind
alcătuit din comutatoare şi relee.
Înlocuirea releelor cu tuburi electronice a constituit un important pas înainte. Rezultatul a fost
concretizat în calculatorul ENIAC ( Electronic Numerical Integrator And Computer ), primul calculator
electronic digital. El conţine circa 18.000 de tuburi electronice şi executa 5.000 de adunări pe secundă,
având o memorie de 20 de numere reprezentate în zecimal. Programarea sa se realiza prin poziţionarea a
circa 6.000 de comutatoare, cu mai multe poziţii. O semnificaţie aparte o are faptul că în arhitectura
calculatoarelor Mark I şi ENIAC, intrau mai multe elemente de calcul, ce lucrau în paralel la o problemă
comună, fiind dirijate de o singură unitate de comandă . Această soluţie a fost aleasă datorită vitezei
reduse a fiecărei unităţi de calcul, în parte. La versiunea următoare s-a renunţat la această structură
paralelă de calcul, deoarece s-a considerat că viteza unei unităţi de calcul, realizată cu circuite
electronice, este suficientă . Soluţia prelucrării paralele a fost reluată ulterior după anii 80’ pentru mărirea
performanţelor unui sistem de calcul; astfel în 1996 Firma INTEL a realizat un supercalculator ce
foloseşte peste 7000 de procesoare PENTIUM utilizând tehnica „de calcul masiv” (utilizat pentru
simularea testelor nucleare, în cercetări genetice, spaţiale, meteorologice).
De remarcat că la realizarea primelor calculatoare, în calitate de consultant al echipei, a lucrat şi
matematicianul John von Neumann, unul dintre matematicienii importanţi ai secolului XX. De altfel, la
realizarea calculatorului EDVAC ( primul calculator cu circuite electronice ) el a stabilit 5 caracteristii
principale ale calculatorului cu program memorat :
 Trebuie să posede un mediu de intrare, prin intermediul căruia să se poată introduce un
număr nelimitat de operanzi şi instrucţiuni .
 Trebuie să posede o memorie, din care să se citească instrucţiunile şi operanzii şi în care
să se poată memora rezultatele.
 Trebuie să posede o secţiune de calcul, capabilă să efectueze operaţii aritmetice şi
logice, asupra operanzilor din memorie.
 Trebuie de asemenea să posede un mediu de ieşire, prin intermediul căruia un număr
nelimitat de rezultate să poată fi obţinute de către utilizator.
41

40.  Trebuie să aibă o unitate de comandă , capabilă să interpreteze instrucţiunile obţinute
din memorie şi capabilă să selecteze diferite moduri de desfăşurare a activităţii
calculatorului pe baza rezultatelor calculelor.
Primul calculator comercializat a fost UNIVAC (UNIversal Automatic Computer ) realizat pe
structura calculatorului EDVAC, în anul 1951. În anii 1960 a apărut un nou tip de calculatoare:
minicalculatoarele. Aceste maşini erau mai ieftine, mai mici, nu avea nevoie de aer condiţionat şi erau
mult mai uşor de folosit (cel puţin după standardele acelor timpuri) faţă de mainframe-uri. În faţă ereziei,
preoţii mainframe-urilor s-au înfiorat. Deţinerea unui mainframe era problema corporaţiei, datorită
cheltuielilor necesare, dar un departament putea avea propriul minicalculator, pentru că acesta nu necesita
spaţii speciale sau specialişti necesari unui mainframe. Pe scurt, minicalculatoarele erau ieftine.Această
dezvoltare a dus la apariţia unui nou personaj pe scena calculatoarelor. Minicalculatoarele au adus la
înlocuirea programatorilor de mainframe, curaţi şi bine îmbrăcaţi, cu o nouă specie de programatori.
Minicalculatoarele au început să fie introduse în universităţi şi alte instituţii de învăţământ, pentru
că erau ieftine. Ele erau accesibile şi proiectate pentru a putea suporta modificări ulterioare, ceea ce a
atras un grup de entuziaşti cunoscuţi sub numele de hackeri. Aceşti hackers nu sunt identici cu cei din
zilele noastre. Acei hacker-i erau plini de entuziasm faţă de calculatoare, oameni care voiau să facă
programe mai bune, mai rapide şi mai „elegante”.Din rândurile lor s-au ridicat o parte din oameni care au
făcut revoluţia calculatoarelor personale. Piaţa minicalculatoarelor a crescut repede. Imediat ce
departamentele puteau justifica nevoia minicalculatorului, acesta era instalat. Acesta a fost momentul
când DEC (Digital Equipment Corporation) a devenit a doua mare companie producătoare de calculatoare
din lume.În privinţa îmbunătăţirilor aduse programelor, gama funcţiilor care pot fi realizate a crescut. Un
minicalculator poate fi folosit simultan de mai mulţi utilizatori, cu ajutorul unui procedeu de împărţire a
timpului de folosire a procesului numit time-sharing. Astfel, fiecare utilizator poate să prelucreze date, să
creeze programe sau să utilizeze, ca şi când ar fi singurul utilizator. Acest sistem a fost introdus şi în
tehnologia de realizare a mainframe-urilor. Sisteme sofisticate de time-sharing, cu componente disc mai
puternice şi programe mai sofisticate, au fost dezvoltate în acelaşi timp pentru mainframe-uri.Aceasta era
piaţa calculatoarelor în anii ´70: mainframe-uri şi minicalculatoare erau prezente în toate companiile şi
principalele departamente. Pentru sacinile pe care le puteau rezolva în moduri în care le rezolvau, erau
bune. Au adus metode noi şi eficiente în birouri şi au făcut afacirele mai eficiente. Totuşi, au eşuat în
mărirea productivităţii personale (în creşterea eficienţei personalului, nu a corporaţiilor).
Apariţia calculatoarelor personale
La mijlocul anilor ´70 a apărut o nouă tehnologie: miniprocesorul. Acesta folosea multe
tranzistoare conectate pe o pastilă de siliciu pentru a realiza un dispozitiv de calcul.Primele
microprocesoare au fost, după standardele actuale, destul de simple. Primul microprocesor, devine
cunoscut ca 4004, a fost proiectat pe patru biţi de către inginerul Marcian E. „Ted” Hoff de la Intel, în
anul 1969. Clientul care i-a comandat lui Intel microprocesorul a fost o firmă japoneză, care a dat
faliment în 1970; după aceasta Intel nu se putea hotărî dacă să lanseze sau nu circuitul pe piaţă. L-au
lansat, şi în 1974 existau mai mult de 19 tipuri de microprocesoare pe piaţă, inclusiv Intel 8088, cel care
va deveni trambulina actualelor calculatoare personale.Microprocesoarele au fost iniţial folosite drept
controler - dispozitive de control – pentru maşini de spălat veselă şi frigidere. Producătorii şi proiectanţii
de calculatoare nu au pierdut ocazia dată de potenţial acestor dispozitive de a fi folosite drept
calculatoare.
8080, Z80, CP/M
Primele succese ale pieţei au fost microprocesorul Intel 8080 şi noul sistem de operare numit
CP/M-80 scris pentru acest cercuit. CP/M-80 a fost creat în 1975 de Gary Kildall, fondatorul şi
preşedintele companiei Digital Research – primul producător al unui sistem de operare pentru
microcalculatoare. Astăzi, compania este o divizie a lui Novell Inc. – cea mai mare companie în domeniul
sistemelor de operare în reţea.CP/M este prescurtat de la Controlul Programului/Microcalculatorului – cel
mai sugestiv nume de produs, dacă mai existase unul, de până atunci. Acest sistem de operare a fost, la
42

41. acea dată, extraordinar. Dacă aveai un sistem 8080 sau Z80, cu sistem de operare CP/M, cu 64 kilobiţi de
RAM şi o pereche de unităţi de disc flexsibil de 8", aveai „ultimul strigăt” al modei calculatoarelor şi îl
făceai verde de invidie pe orice pasionat. Un singur lucru le putea depăşi invidia şi cîştiga ura: să ai un
disc şi o imprimată; ambele necesitau o cheltuială exorbitantă.Discurile acelor timpuri merită puţină
atenţie. Primul tip larg răspândit împreună cu microcalculatoarele aveau discuri de 14" (comparaţi-le cu
cele de 3,5" disponibile astăzi) şi un timp de acces suficient pentru o pauză de cafea.
Apple Computer, binecunoscută ca avându-şi începuturile într-un garaj, a apărut în 1976. Apple a fost
fondată de legendarii Steve Jobs şi Steve Wozniack, şi este recunoscut drept compania care a pus bazele
industriei calculatoarelor personale. Deşi povestea lui Visilac şi a calculatorului Apple II este bine
cunoscută, merită să o spunem încă o dată, pentru că arată motivele care au generat revoluţia
calculatoarelor personale.La mijlocul anilor `70, dacă doreai să faci încercări de genul „şi dacă” calculând
pe mainframe, trebuia să scrii un program, să-l depanezi, să încerci un set de date, să verifici rezultatele,
să încerci un set de date mai complex s.a.m.d. Era un procedeu cel puţin laborios şi nu foarte practic, cu
excepţia cazului în care priviziunele aveau importanţă pentru corporaţie şi aveai suficient timp la
dispoziţie. Această situaţie a motivat doi studenţi de la Harvard Business School să facă primul program
de calcul tabelar: Visicalc.Apple II avea la bază un procesor Motorola 6502 (proiectat pe 8 biţi), până la
128 kilobiţi de RAM şi utiliza un casetofon pentru a stoca date şi programe. Apple a încheiat o înţelegere
cu realizatorii lui Visicalc pentru a obţine exclusivitatea programului pe Apple II. Acestui program i se
acordă meritul de a fi catapultat Apple de la un venit de 800.000 de dolari în 1977 la puţin sub 48 de
milioane în 1979.Utilizatorii cumpărau Apple II doar pentru a rula Visicalc, şi o dată cu el un raft întreg
de aplicaţii, care ofereau utilizatorilor, pentru prima dată la un preţ rezonabil, putere de calcul accesibilă
şi dedicata
IBM preia controlul
Calculatoarele despre care am vorbit, maşinile CP/M şi Apple, nu erau numite calculatoare
personale – acesta nu a fost un termen recunoscut până în august 1981, data de naştere a calculatorului
IMB PC a fost creat de piaţă, datorită acelor sisteme de microcalculatoare care au făcut posibilă existenţa
calculatorului IBM PC.Deşi microprocesorul care a stat la bază calculatorului IBM PC a fost produs în
1974, calculatorul IBM PC a fost produs abia în 1981. Intel 8088 era un microprocesor pe 16 biţi, care
putea lucra cu mai multă memorie şi mai rapid decât predecesorii săi. IBM a delegat o companie
necunoscută, numită Microsoft, pentru a realiza un sistem de operare. Restul este, aşa cum o spun ei,
istorie. IBM PC a devenit un standard, în realitate o serie de standarde care au adus la vânzarea de
aproximativ 100 de milioane de calculatoare personale din 1981. puterea marketing-ului IBM a dus la
succesul lui IBM PC. IBM avea bani şi poziţia pe piaţă astfel încât să facă calculatorul IBM PC acceptat
în corporaţii. Deşi e uşor să critici IBM pentru greşelile, destul de multe, făcute în dezvoltarea pieţei
calculatoarelor personale şi lipsa de receptivitate faţă de o piaţă care creştea mai rapid decât putea acoperi
IBM, fără amestecul lui IBM, această piaţă ar fi crescut mult mai încet şi mai fragmentat.
Calculatorul IBM PC a continuat tendinţa dată de Apple II, aducând puterea de calcul la îndemâna
utilizatorilor. Posibilitatea de a-şi îmbunătăţi şi mări productivitatea personală a fost o atracţie atât de
mare, încât oamenii au trecut peste orice pentru a-şi cumpăra un calculator personal. Ei au păcălit
bugetele departamentale cumpărându-le ca maşini de scris sau chiar plătind diferenţa din propriul
buzunar.
Multe companii au avut reţineri în a urma tendinţa de introducere a calculatoarelor personale, dar
au descoperit ulterior că acestea erau folosite din plin de concurenţa. În aceste companii, de obicei,
Centrul de Calcul era uluit când descoperea invazia calculatoarelor personale. Fanaticii mainframe-urilor
erau probabil cei mai surprinşi când aflau ce se întâmplase.
Aparent peste noapte, Centrul de Calcul pierdea un procent destul de mare din prelucrările de date
ale companiei. Teritoriul pe care credeau că îl stăpânesc era brusc invadat. Ceea ce era probabil cel mai
tulburător pentru ei era că utilizatorii de calculatoare personale vorbeau despre informaţii şi nu doar
despre coloane de date.
43

42. Utilizatorii au descoperit că puteau combina şi prelucra cum doresc datele. Puteau realiza rapoarte
despre ceea ce îi interesa. Pe de altă parte, dacă ai fi cerut la Centrul de Calcul un raport, ţi-ar fi dat doar
un raport standard aşa cum le genera mainframe-ul. (Rapoartele standard consumau o „mică pădure” de
hârtie, când toţi utilizatorii doreau doar o pagină ).
Astfel a apărut o nouă tendinţă: aceea de a a-ţi realiza singur calculele. Atunci când utilizatorii
doreau să facă simulări financiare de tipul „şi dacă”, ei nu mai trebuiau să meargă, cu pălăria în mână
(metamorfic vorbind) la Centrul de Calcul. Puteau să-şi pornească calculatorul personal, să ruleze
programul de calcul tabelar şi să realizeze o duzină de scenarii, în timpul în care Centrul de Calcul ar fi
luat în considerare cererea lor.Deja nu mai exista nici o posibilitate pentru Centrul de Calcul de a
schimba lucrurile. Corporaţiile aveau toate motivele să susţină noua tendinţă şi în acelaşi timp destule
motive de îngrijorare pentru anarhia care se crea. Distribuirea datelor prin companii, cum veţi vedea, avea
multe implicaţii şi exista marele risc de a scăpa totul de sub control.
Revoluţia calculatoarelor personale, mai mult decât orice, a forţat Centrele de Calcul să-şi
regândească rolul şi tehnologia pe care o foloseau. Ele nu au avut cu adevărat de ales şi au devenit
Servicii de gestiunea de informaţie (Management Information Service) sau IT (Information Tehnology)
sau orice altceva care conţinea cuvântul informaţie. De asemenea, au trebuit să urmeze sau cel puţin să se
obişnuiască cu valul tehnologiilor aduse de calculatoarelor personale.
Începutul conectării
Pe timpul CP/M-ului, preţul perifericilor de calitate era exorbitant. Un disc de 14" şi 10MB, care
consuma 5 amperi şi făcea zgomot ca un avion care decola, era tot atât de scump ca şi un calculator. O
imprimată matriceală, care nici nu se apropia de calitatea unei letter-quality, era o resursă preţioasă. În
momentul lansării calculatorului IBM PC preţurile scăzuseră, dar erau încă destul de mari. Pe scurt,
perifericele calculatoarelor personale erau ca aurul: rare şi scumpe.
Nu era practic ca fiecare calculator să aibă disc şi imprimată, deşi fără ele productivitatea calculatoarelor
personale era mai mică. O altă problemă era folosirea în comun a datelor. Dacă aveai nevoie de un
document creat de altcineva, trebuia să iei dischetă, să-ţi pui pantofii de sport şi să alergi la acel
microcalculator să-l iei. De aici, numele acestui tip de partajare a datelor: „reţea sportivă”.
„Reţeaua sportivă”
Acest tip de reţea a ridicat multe probleme. Cum puteai să fii sigur că documentele cu care lucrai
erau la zi, dacă diverse copii modificate de un număr oarecare de oamenii circulau pe diverse dischete?
Cum poţi opri furtul documentelor? Cum poţi opri furtul documentelor? Şi dacă ultima versiune, şi
singura, a unui document se află pe o singură dischetă folosită de cineva drept suport pentru ceaşcă de
cafea? Şi dacă...?
Existau sute de probleme cu această reţea şi toate evidenţiau o singură soluţie: nevoia, absolută necesitate,
de a schimba documentele electrice între calculatoare. Combinaţi cu dorinţa de a schimba, de a folosi în
comun discuri şi imprimate scumpe, şi aveţi o problemă la care să meditaţi. Nevoia de a folosi în comun
date şi periferice a stimula crearea primei reţele locale de calculatoare, dar aşa cum veţi vedea, problema
centrală a fost nevoia de a folosi în comunicatie.
Comutatoarele de date
O modalitate de a folosi în comun periferice a fost folosirea unui comutator de date: un dispozitiv
ce permite doar unui utilizator la un moment dat să folosească dispozitivul, ca exemplu o imprimată.
Dacă o altă persoană folosea imprimata când doreai tu să o foloseşti, trebuia să aştepţi până termina. Un
comutator de date poate fi comparat cu o coadă la bancă. Orice persoană (datele ce vor vi imprimate) care
se aşează prima coadă (comutatorul) ajunge prima la casier (imprimanta). Restul trebuia să aştepte până
ce aceasta termină.
Comutatorul de date oferă utilizatorului o conexiune pe portul serial sau paralel, pe bază căreia
primul utilizator care cere primeşte dreptul de folosi imprimanta. Calculatorul care nu mai are nevoie de
periferic trebuie să trimită o secvenţă de caractere prin care spune de fapt „Am terminat”.
44

43. Aceste dispozitive, deşi erau bune pentru imprimantă şi plotere (ele încă mai sunt folosite – câteva
companii încă le mai oferă ), nu permiteau folosirea în comun a discurilor. De asemenea, necesitau o linie
dedicată între calculator şi comutator. Aceasta devenea dificil de realizat când calculatoarele erau
răspândite pe o suprafaţă mare, şi imposibil dacă erau mai multe calculatoare.
„Aici servesc discuri”
Prima încercare de a realiza ceea ce astăzi numim reţea locală (LAN) a fost tehnologie, acum
învechită, numim disc server. Un disc server era un calculator, prin care, printr-o tehnică de comunicaţie
oarecare, era legat de un grup de calculatoare numit clienţi. El rula un sistem de operare special care era
proiectat astfel încât să poată permită accesul mai multor clienţi în acelaşi timp la disc şi la imprimată:
acest sistem se numeşte sistem de operare pentru reţea (Network Operating System sau NOS).
Funcţionarea reţelei
Aplicaţia client/server
Primele aplicaţii de reţea erau în majoritate programe integrate. De exemplu, dacă ofereau o bază
de date multiutilizator ele aveau şi partea frontală (front-end) de interacţiune cu utilizatorului şi „motorul”
bazei de date (partea de program care lucra cu fişierele bazei de date) pe acelaşi PC. Singura parte care se
putea afla în reţea, pe server, era baza de date.
În această configuraţie, calculatorul client realiza toată prelucrarea datelor (citire, căutare a
înregistrărilor dorite între datele citite etc.). Aplicaţiile acestea pot fi descrise ca având doar client.
Serverul era o simplă „pompă” de date: trimitea utilizatorului date din fişierele aflate pe disc sau le
primea şi le stoca pe disc.
În ultimii ani au apărut un număr mare de sisteme de bază de date sofisticate care pun în reţea
„motorul” de acces la baza de date care se află în parte frontală (front-end) utilizatorul. Acestea se
numesc sisteme client/server.
O dată cu îmbunătăţirea performanţelor datorită eliminării supraîncărcării reţelei cu transferuri
mari de date, mai există şi avantajul faptului că serverul poate deservi mai mulţi clienţi în acelaşi timp.
Întregul proces de sincronizare al accesului la baza de date, care trebuia realizat de clienţi, este acum
realizat de server, ceea ce face aplicaţiile mai simple şi întregul sistem mai eficient.
Bazele de date nu sunt singurele aplicaţii care pot fi realizate în sistem client/server. Alte aplicaţii
client/server includ servere de poştă electronică, sisteme de vizualizare pe calculator a imaginilor şi
urmărire serviciilor de reţea.
Avantajele sistemelor client/server sunt următoarele:
 securitate mai bună, deoarece accesul la datele din baza de date server este indirect.
Utilizatorii nu pot vedea fişierele de date decât dacă li se dă acest drept în mod explicit.
 Performanţele pot fi îmbunătăţite uşor, deoarece o mai bună proiectare a serverului
poate duce la o mai bună coordonare a utilizatorilor care doresc servicii în acelaşi timp şi,
de aici, performanţe mai bune. În cazul severelor de baze de date prin reţea pentru a găsi ce
îi interesează; e suficient ca ele să trimită cereri către server, iar serverul le va trimite doar
rezultatele pe care le doresc.
Creşte raportul calitate/preţ. Clienţii trebuie doar să aibă suficientă putere de calcul pentru a rula
partea frontală (front-end). (Când sunt necesare performanţe mai mari, serverul poate fi înlocuit cu un
calculator personal mai performant şi, respectiv, mai scump).
Dezavantajele sistemelor client/server:
 Complexitatea: nu este simplu, de obicei, să configurezi şi să administrezi sisteme
client/server.
Necesităţi: pentru a avea mulţi utilizatori, serverul din sistemele client/server are nevoie de un
calculator scump. Aplicaţiile de pe server au tendinţa să devie mai mari şi mai complexe şi au nevoie de
mai multă memorie RAM.
Preţ: performanţele serverului scad o dată cu creşterea numărului de utilizatori. Pentru a reface
performanţele, serverul de bază de date trebuie să ruleze pe o maşină dedicată acelui server. Deci, acolo
45

44. unde cândva era un server dedicat general, care funcţiona şi ca server de bază de date, acum avem un
server dedicat general şi un server de baze de date dedicat, ceea ce duce cel puţin la dublarea costului.
Tehnologii de grup
Tehnologiile de grup (groupware) sunt un set de tehnologii care au scopul de a îmbunătăţi
productivitatea a doi sau mai mulţi utilizatori care cooperează în realitate unor obiective comune. Ideea
este ca o dată ce reţeaua uneşte utilizatorii, munca şi comunicările cu privire la ea pot fi automatizate
pentru îmbunătăţirea fluxului muncii şi a oportunităţilor. Teoretic, un grup de oameni care muncesc
împreună într-o activitate comună sau pentru obiective comune poate fi mult mai eficient decât un grup
de oameni care muncesc independent. Deoarece calculatoarele îmbunătăţesc dialogul între membrii
grupului şi urmăresc progresele lor, detaliile nu vor mai fi omise, iar desfăşurarea poate fi foarte uşor de
urmărit.
Aceste idei au fost aplicate la procese cum sunt planificate şi administrate proiectelor. Planificarea
în reţea permite unui grup dintr-o reţea să-şi facă orare pe reţea. Când vor să-şi coordoneze activităţile, de
exemplu să stabilească o întâlnire, orarul grupului poate fi examinat şi poate fi găsit momentul când toţi
membrii sunt disponibili. Folosind poşta electronică, aceştea pot fi rugaţi să va şedinţă (sau în
organizaţiile mai autoritate li se ordonă).
Alte caracteristici ale aplicaţiei de grup:
 Sisteme de informare (oferite în sisteme de poştă electronică cum ar fi cc: Mail).
 Baze de date folosite în comun.
 Sisteme de conducere a proiectelor.
 Servicii de bibliotecă (pentru administrarea documentaţiilor aparţinând unui grup).
 Sisteme de control al versiunii (asemănătoare cu serviciul de bibliotecă, dar cu facilităţi
de control al arhivării şi găsirii diverselor versiuni de fişier; aceste sisteme sunt de obicei
folosite pentru dezvoltarea programelor).
Una dintre cele mai lăudate aplicaţii ale tehnologiilor de grup, Lotus Notes, este un sistem de baze
de date cu poştă electronică. Rolul lui Notes este de a răspândi informaţiile deţinute în bazele de date ale
organizaţiilor, la un număr oarecare de utilizatori. Sistemul permite duplicarea şi sincronizarea mai multor
copii de baze de date.
O altă direcţie principală a aplicaţiilor de grup este posibilitatea urmăririi fluxului muncii. Ideea
este că grupurile de utilizatori care sunt într-o reţea pot beneficia de automatizarea activităţilor de rutină.
Mare parte a sistemelor care se ocupă de fluxul muncii se bazează pe formulare. Ele primesc date de la o
persoană, pe care apoi le transmit, dacă e posibil cu date suplimentarea din alte surse, celorlalţi membri.
Ele au mecanisme pentru contabilizarea şi urmărirea tranzacţiilor şi raportarea stadiului muncii.
Obiectivele vor fi mai rar uitate sau amânate, deoarece calculatoarele sunt mai de încredere decât
oamenii. Fluxul muncii este concept atât de important în reţele, încât multe dintre principalele companii
producătoare de produse de reţea au investit în companii care dezvoltă tehnologii de bază pentru suportul
fluxului muncii.
Problema cu aplicaţiile de grup este că e greu ca oamenii să se obişnuiască cu ea! („Poţi să duci un
cal la apă, dar nu poţi să-l faci să bea.”).
NIVELE ALE LIMBAJELOR DE PROGRAMARE
“Nivelul” unui limbaj este apreciat prin poziţia pe care o ocupă pe scara constituită de limbajul
recunoscut de microprocesor (limbaj maşină) şi limbajul natural al programatorului (limba română, limba
engleză …) .
Un limbaj de nivel scăzut este foarte apropiat de maşină, el manipulează cu elemente de nivel
hardware, fizic, cum ar fi : registru, microprocesor, locaţie de memorie, port de intrare / ieşire etc.
Un limbaj de nivel înalt sau foarte înalt manipulează cu concepte apropiate de limbajul natural,
concepte de nivel logic, cum ar fi: colecţie de date, nume de operaţie (sort, writeln, open), variabile,
constante ( asemănătoare ca înţeles cu cele din matematică).
46

45. Cu ajutorul unui limbaj de nivel înalt programatorul se face mult mai uşor înţeles de către
calculator . Uneori o singură limie de program scrisă cu un astfel de limbaj poate echivala cu sute de linii
de program scrise în limbaj maşină. Deci din punct de vedere al reducerii timpului de realizare a unui
program şi al siguranţei în funcţionare (absenţa erorilor de programare) este de preferat un limbaj de nivel
cât mai ridicat (înalt sau foarte înalt). În schimb, pe măsură ce limbajul are un nivel mai ridicat execuţia
programului conceput cu ajutorul său va fi mai lentă, decât a unui program ce realizează aceleaşi operaţii
dar este scris în limbaj de asamblare.
O altă diferenţă esenţială între cele două tipuri de limbaje o reprezintă portabilitatea, adică
posibilitatea transferării programelor pe un alt tip de maşină decât cea pe care au fost construite. Din acest
punct de vedere limbajul de asamblare este neportabil deoarece el este specific microprocesorului.
Programele realizate pe un tip de maşină trebuie rescrise integral pentru noul tip de maşină , folosind un
nou set de instrucţiuni – care deobicei diferă foarte mult. Lucrurile stau altfel cu programele concepute cu
ajutorul unui limbaj de nivel înalt, deoarece acestea sunt detaşate de maşină. Între un astfel de program şi
calculator se interpune compilatorul (sau interpretorul) care rezolvă corect transformarea fişierului-sursă
în fişier - executabil.
Limbaje procedurale – neprocedurale
Cele două tipuri de limbaje, procedurale şi neprocedurale, se diferenţiază prin nivelul de
organizare (structurare) a unui program. Limbajele neprocedurale sunt concepute pentru a gândi un
program la nivel de instrucţiune, pe când cele procedurale, obligă programatorul să conceapă programe la
nivel de bloc. Într-un limbaj procedural (numit şi limbaj structurat) programele sunt scrise instrucţiune cu
instrucţiune, dar ele sunt organizate logic în blocuri (grupuri de instrucţiuni) ce realizează o acţiune bine
determinată. În general un bloc are un punct de intrare şi un punct de ieşire – nu mai multe.
Un limbaj procedural oferă posibilitatea utilizării unui nivel ridicat de concepere a unui program şi
duce la realizarea de programe coerente şi protejate la erori. Prin contrast, limbajele neprocedurale nu
favorizează programatorul în a se desprinde de nivelul „instrucţiune” şi duc deseori la programe greu de
controlat – mai ales în cazul programelor de dimensiuni mari.
Limbajele neprocedurale sunt încă preferate de unii utilizatori datorită timpului foarte scurt cât
decurge învăţarea şi utlizarea lor.
Limbaje orientate
Din punctul de vedere al aplicabilităţii unui limbaj, limbajele pot fi orientate pe o anumită
problemă sau concepute pentru soluţionarea oricărui tip de problemă – limbaje de uz general sau altfel
spus, neorientate pe o problemă.
Limbajele orientate prezintă un grad înalt de specificitate pe când un limbaj neorientat reprezintă
un cadru general ce permite introducerea de către utilizator a conceptelor şi prelucrărilor dorite.
Deci, diferenţa esenţială dintre cele două tipuri de limbaje o constitue nivelul conceptual definit.
Cele specializate posedă deja integral suportul necesar şi permit programatorului să se concentreze la
ansamblul problemei, pe când cele nespecializate lasă în sarcina programatorului manevrarea nivelelor
inferioare ale problemei.
Limbaje concurente
Un limbaj concurent permite definirea de procese (prelucrări) paralele, execuţia sa fiind ramificată
la un anumit moment de timp. Prin contrast limbajele neconcurente (majoritatea limbajelor) au o
desfăşurare liniară, fiind activ un singur proces la un moment dat. Procesele concurente presupun în mod
obligatoriu un sistem multi-tasking ce poate gestiona mai multe „sarcini” la un moment dat.
Limbaje de nivel scăzut
Această categorie de limbaje are un reprezentant autoritar şi anume: limbajul de asamblare.
Diferenţierile care se pot face pentru limbajele de nivel scăzut sunt următoarele:
47

46.  după tipul de maşină;
Regulile respectate de versiunile limbajului de asamblare sunt :
– nouă versiune o include complet pe cea anterioară,
– versiunea nouă oferă funcţii suplimentare şi le realizează pe cele vechi mai rapid.
 după mediul de programare oferit.
Aspectul unui limbaj poate fi schimbat radical de mediul de programare oferit . Pentru limbajul de
asamblare există mai multe implementări disponibile, începând cu pachete ce operează în mod linie şi
culminând cu medii integrate în care toate operaţiile se pot declanşa de la un acelaşi pupitru de comandă .
Nu sunt luate în considerare decât aceste medii integrate (denumite generic medii Turbo), dintre
care se detaşează Turbo Asamblorul firmei Borland TASM.
Limbaje de nivel înalt neorientate
BASIC
A fost creat în 1964 la Darmooth College (S.U.A.). Denumirea sa provine de la iniţialele
cuvintelor Beginner’s Allpurpose Symbolic Instruction Code (Cod de instrucţiuni simbolice, de uz
general, destinat începătorilor).
Are următoarele caracteristici fundamentale :
– simplu de învăţat; instrucţiunile sale sunt cuvinte din limba engleză sau prescurtări ale
acestora;
– neorientat pe un anumit tip de problemă; permite construirea de aplicaţii;
– este un limbaj nestructurat, ceea ce îi permite să fie uşor învăţat.
Din cauză că a cunoscut o largă răspândire, au fost implementate noi versiuni de Basic: GW-
BASIC, QUICK BASIC, TURBO BASIC, VISUAL BASIC (Basic for Windows).
FORTRAN
Limbajul Fortran este decanul de vârstă al limbajelor de largă folosinţă. A apărut în 1956 şi îşi
datorează numele prescurtării cuvintelor: FORmula TRANslation (Traducere de formule). Iniţial
reprezenta un limbaj orientat pe calcule ştiinţifice având definite concepte precum: matrice, funcţii
trigonometrice, numere reale în dublă precizie. Versiunile ulterioare care au cunoscut o mare popularitate
au extins posibilităţile limbajului trasformându-l într-un limbaj eficient, de uz general. În prezent există
pentru IBM-PC două implementări mai importante ale limbajului: Microsoft Fortran, Fortran for
Windows.
Deşi nu poate fi considerat „depăşit” din punct de vedere conceptual (este un limbaj algoritmic –
structurat) este neindicată folosirea lui datorită absenţei unor medii de programare performante şi pentru
că tendinţa actuală îi este defavorabilă.
PASCAL
Conceptualizat în anul 1970 de către Niklaus Wirth, limbajul PASCAL poartă numele
matematicianului şi filosofului BLAISE PASCAL, în semn de recunoaştere a meritelor sale în
teoretizarea maşinilor de calcul.
Creat după acumularea de cunoştiinţe temeinice în ştiinţa limbajelor formale, din confruntarea cu
probleme concrete ale programării, limbajul PASCAL a constituit la vremea respectivă un limbaj modern,
menţinându-se ca atare şi în prezent, datorită faptului că posedă o solidă bază conceptuală.
Limbajul PASCAL a introdus în versiunea sa iniţială noţiunea de programare structurată şi
ulterior noţiunile de date (structuri) dinamice, date (structuri) definite de utilizator.
În prezent standardul implementărilor PASCAL cuprinde următoarele elemente:
 programare structurată de tip algoritmic;
 definirea de noi funcţii sau proceduri;
 tipuri de date definibile de către utilizator;
 structuri de date dinamice;
48

47.  adresări indirecte ale datelor;
 recursivitate;
 rutine complete de intrare / ieşire;
 funcţii de conversie a datelor din ASCII în format intern şi invers;
 set complet de funcţii matematice;
 funcţii elementare de grafică 2D;
 posibilitatea inserării direct în sursă a instrucţiunilor în limbaj de asamblare;
 posibilitatea definirii de overlay-uri pentru program.
Versiunile standard ale implementărilor PASCAL sunt cele oferite de Microsoft şi Borland, cu
avantaj pentru cele din urmă (TURBO PASCAL 5.0, TURBO PASCAL 5.5) datorită mediului de lucru
performant (de tip “TURBO” ). Combinaţia PASCAL + TURBO a reprezentat un succes imens în rândul
programatorilor având ca singur rival cealaltă combinaţie: C+TURBO.
Limbajul C
Acest limbaj de programare , cu cel mai scurt nume , a fost creat în 1971 de către Dennis Ritchie
şi Brian Kernigham pentru dezvoltarea sistemului de operare UNIX.
Principalele caracteristici ale limbajului sunt:
 limbaj structurat de nivel înalt;
 posedă concepte de nivel scăzut, ceea ce permite exploatarea portabilă a caracteristicilor
intime unei maşini;
 rutine de conversie a datelor foarte evoluate;
 tipuri de date definibile de către utilizator;
 gestionarea elaborată a datelor de tip dinamic;
 definirea de noi funcţii;
 adresări indirecte ale datelor , variabilelor ( pointer-i );
 recursivitate;
 set complet de funcţii matematice;
 funcţii pentru realizarea de grafică elementară 2D;
 funcţii de apel servicii DOS;
 posibilitatea definirii de overlay-uri pentru un program;
 concizie deosebită a limbajului.
 Pentru versiunile standard ale implementărilor limbajului C există medii de programare
de tip “TURBO” ce aparţin firmelor: Microsoft – produsul QUICK C şi firmei Borland –
produsele TURBO C.
Limbajul ADA
A fost creat special pentru a gestiona totalitatea aplicaţiilor dezvoltate şi utilizate de N.A.S.A.
Noutatea limbajului (de tip structurat, algoritmic) o constitue concurenţa, deci posibilitatea lansării de
procese paralele (sincronizate interactiv în finalul execuţiei lor). Saltul calitativ este evident şi deschide
un nou domeniu în programare … dar nu pentru IBM-PC. Versiunile implementărilor limbajului ADA pe
IBM-PC nu posedă tocmai acestă parte de concurenţă, reducând limbajul la un simplu limbaj structurat de
uz general. Deci, ADA este un limbaj ultramodern din punct de vedere teoretic dar ineficient din punct de
vedere practic pentru IBM-PC-uri.
Limbaje orientate pe gestiunea bazelor de date
Necesităţile actuale în practica utilizării calculatoarelor se îndreaptă cu precădere spre gestionarea
bazelor de date de mari dimensiuni. O explicaţie a acestei orientări e dată de faptul că o bază de date
reprezintă o informaţie, iar cel ce deţine informaţii complete şi rapide într-o anumită problemă este
49

48. indiscutabil cu un pas înaintea celorlalţi. Concurenţa din domeniul economic poate fi numită pe bună
dreptate o bătălie informaţională.
Un sistem de gestionare a bazelor de date (S.G.B.D.) de tip clasic operează cu următorii termeni
fundamentali:
 câmp – o locaţie în care se poate memora o informaţie bine determinată;
 înregistrare – mai multe câmpuri alcătuiesc împreună o înregistrare;
 baza de date – colecţie de înregistrări.
Deci, datele sunt gestionate prin intermediul unei structuri, organizată ierarhic, la un nivel de
organizare logică.
Tendinţa modernă în exploatarea bazelor de date constă în deplasarea interesului către bazele de
date relaţionale. Diferenţa esenţială constă în definirea unui nivel logic suplimentar între datele
gestionate. Acestea nu mai sunt privite ca simple fişe izolate între ele ci pot fi analizate pe baza legăturilor
(relaţiilor) ce există între ele.
Noţiunile cu care operează un S.G.B.D. relaţional sunt următoarele:
 tabel – structură fundamentală de “depozitare” a datelor;
 linie în tabel – echivalentul unei înregistrări clasice;
 coloană în tabel – echivalentul unui câmp de tip clasic;
 bază de date – o colecţie de tabele, conectate prin valorile anumitor coloane.
Această nouă concepţie permite definirea de structuri 1:n. O “înregistrare” poate conţine n valori
pentru un “câmp” anumit nu una singură ca în cazul clasic. Structurile de tip 1:n pot fi rezolvate şi cu
ajutorul unui S.G.B.D. clasic, dar întreaga gestiune a operaţiilor revine programatorului pe când un mediu
relaţional furnizează din start servicii speciale.
Spre deosebire de S.G.B.D.-urile clasice, un mediu relaţional presupune ca cerinţă minimală
posibilitatea manipulării datelor prin intermediul conexiunilor logice stabilite. Pentru aceasta există
definit (şi impus ca standard unanim recunoscut) limbajul de interogare SQL (Structured Query
Language – limbaj de cereri structurate). Prin intermediul său sunt permise următoarele operaţii:
 regăsire date (conexate logic) ce îndeplinesc o anumită condiţie;
 definire ordine de returnare a datelor;
 redefinire conectări logice ale datelor;
 exploatare;
 programare.
Avantajele unui S.G.B.D. clasic sunt:
 simplitate în manevrare; deci efort de studiu redus;
 pot funcţiona pe un sistem de calcul ce nu implică resurse speciale, ci doar spaţiu de
stocare extern suficient pentru problema dată;
 preţ de cost redus faţă de cele relaţionale.
Avantajele unui S.G.B.D. relaţional sunt:
 nivel logic superior (corelaţii, structuri 1:n ),
 prelucrări (regăsiri) de date cu un înalt nivel de complexitate;
 nivel superior de portabilitate a aplicaţiilor, datelor.
S.G.B.D. -uri clasice
dBASE III
Cel mai răspândit sistem de gestiune a bazelor de date este dBASE, în diversele lui versiuni. El
poate fi considerat un “BASIC” al bazelor de date. La momentul apariţiei a constituit o adevărată
revoluţie în domeniul S.G.B.D.-urilor.
Meritele sale principale care l-au impus atenţiei utilizatorilor şi programatorilor sunt :
 foarte simplu de utilizat;
 limbaj de nivel foarte înalt , simplu de învăţat;
50

49.  interactivitate bună a sistemului;
 poate funcţiona cu resurse extrem de restrânse;
 Dezavantajele principale ale dBASE-ului sunt:
 viteză de lucru extrem de scăzută;
 limbaj de programare cu lacune greu de surmontat (nu posedă salturi, funcţii
matematice reduse, erori de implementare);
 aplicaţiile create slab interactive;
 imposibilitateta conectării cu un alt limbaj.
Cele mai importante implementări ale sale sunt: dBASE III Plus şi dBASE IV.
COBOL
A fost creat în 1950 şi reprezenta singura posibilitate de gestionare a unei baze de date. Reprezintă
în primul rând un limbaj de programare special conceput pentru informatica de gestiune. Dacă facem o
comparaţie, sugestivă, COBOL este echivalentul FORTRAN-ului pentru sistemele de gestiune a bazelor
de date (din punct de vedere istoric şi al performanţelor).
Limbajul este considerat greoi şi inflexibil, iar pentru crearea unui program foarte simplu e nevoie
de scrierea unui adevărat eseu.
Singurul avantaj real al COBOL-ului este portabilitatea sa ridicată.
FOXBASE
Sistemul dBASE a incintat firmele producătoare de soft, datorită popularităţii sale şi pe de altă
parte a calităţilor scăzute ale implementărilor originale furnizate de firma Ashton-Tate. Au apărut noi
implementări ale limbajului care au încercat să furnizeze unelte profesionale pe baza acestui suport
conceptual.
Versiunile FOXBASE 2.10 şi FOXBASE PRO se constitue în medii performante atât pentru
programatori cât şi pentru utilizatori.
ISIS
Este distribuit gratis de către UNESCO, ceea ce îl face cu adevărat interesant. Caracteristicile ce îl
fac interesant sunt:
 interactivitate bună;
 posibilitate definire structuri 1:n;
 suport de reţea locală;
 un limbaj intern (o versiune de PASCAL) cu care se prelucrează datele;
 adaptabilitate foarte bună.
S.G.B.D. –uri relaţionale
ORACLE
Se poate afirma fără teama de a greşi că ORACLE reprezintă cel mai performant S.G.B.D.
disponibil la momentul actual. Pe lângă faptul că posedă avantajele unui mediu de tip relaţional ORACLE
este gândit ca un sistem exhaustiv pentru rezolvarea problemelor de utilizare sau programare.
Limbajul intern folosit este SQL Plus şi este permisă conectarea cu alte limbaje externe evoluate
(orientate către C). Putem menţiona:
 viteză de lucru foarte bună;
 exploatare interactivă la nivel SQL;
 limitări de lucru greu sau imposibil de atins (maxim 65535 caractere într-un câmp,
număr nelimitat de câmpuri, de înregistrări);
 exploatare eficientă a spaţiului pe disc (memorarea câmpurilor în format variabil).
Oracle este implementat pe majoritatea tipurilor de computere mari, ceea ce oferă portabilitatea
aplicaţiilor, dar mai ales posibilitatea conectării la calculatoare puternice.
PARADOX
51

50. Reprezintă un S.G.B.D. cu adevărat profesional. El îndeplineşte toate cerinţele unui produs cu
adevărat modern şi performant şi anume:
 interactivitate foarte bună;
 viteză de lucru mare;
 servicii şi auxiliare;
 limbaj de programare evoluat (PAL – Paradox Application Language), dotat cu
compilator.
Limbaje orientate pe calcul tabelar
Aplicaţiile împreună cu limbajele implementate pentru rezolvarea problemelor descrise în
continuarea nu pot fi considerate medii de programare propriu-zise.
Aplicaţiile de tip „tabelă de calcul” au fost concepute în ajutorul funcţionarilor, pentru a prelua o
parte imensă din rutina de lucru inerentă unor astfel de activităţi.
Denumirea provine din limba engleză şi este o traducere pentru termenul „spread-sheet” (spread-
întindere, desfăşurare, foaie, tabel; sheet-schemă, diagramă, a acoperi cu un strat). În traducere directă
aceasta ar însemna – pentru cazul de faţă – organizarea unei foi (a unui tabel).
Iată cum funcţionează un program de tip spread-sheet:
 elementul de lucru îl reprezintă un tabel;
 un tabel este format din linii şi coloane;
 intersecţia unei linii cu o coloană se cheamă celulă;
 tabelul este vizualizat pe ecran prin intermediul unei ferestre;
 în fiecare celulă poate exista una din entităţile următoare: text, numere, formule,
secvenţe de program, macroinstrucţiuni.
Pe lângă aceste caracteristici specifice unui spread-sheet cerinţele minimale ale unui pachet de
calcul tabelar includ:
 posibilitatea „căutărilor inverse” (de la rezultatul unui calcul, la valorile care l-au
generat);
 posibilitatea de lucru multi-tabel (mai multe tabelel simultan);
 funcţii de editare şi formatare a textului (editor de texte obişnuit);
 funcţii grafice (diagrame, prezentări);
 sistem de gestiune a bazelor de date (pentru celulele unui tabel);
 tipărire de calitate (posibilitatae de a lucra cu mai multe tipuri de imprimante,
exploatarea rezoluţiei unei imprimante laser, set bogat de fonturi).
Spre deosebire de limbajele de programare propriu-zise, cele folosite de spread-sheet-uri sunt
special concepute pentru a fi folosite de nespecialişti (uşor de învăţat, uşor de utilizat).
Un astfel de limbaj (de tip interpretor) se constituie într-un cadru general pentru rezolvarea
problemelor funcţionarilor din diverse domenii de activitate.
O aplicaţie realizată cu un spread-sheet poate fi modificată şi adusă la zi direct de către utilizator,
fără a mai fi necesară intervenţia programatorului. Produsul obţinut are flexibilitate maximă, iar efortul
necesar realizării lui este minim.
Dezavantajele principale ale aplicaţiilor realizate cu ajutorul unui spread-sheet le constitue
imposibilitatea depăşirii cadrului de „programare” oferit şi dificultatea de a realiza prelucrări foarte
complexe . Însă aceste dezavantaje sunt mai mult teoretice deoarece nu este cazul de a realiza aplicaţii cu
astfel de cerinţe folosind un spread-sheet. Programele de calcul tabelar rezolvă în mod strălucit o
problemă punctuală.
Cele mai cunoscute şi răspândite produse de tip „calcul tabelar” sunt:
LOTUS 1-2-3
Lotus 1-2-3, produs al firmei Lotus Development este în mod sigur cel mai răspândit produs din
această categorie. Datorită popularităţii sale el s-a constituit într-un adevărat standard (neoficial) pentru
52

51. spread-sheet-uri. La nivel de ansamblu, LOTUS se preuintă ca o aplicaţie cu bună interactivitate.
Reproşurile ce i se pot aduce sunt: meniurile (uneori stufoase şi nelogic ramificate) şi help-ul care nu
totdeauna este la obiect.
QUATRO PRO 2.0
Spread-sheet-ul QUATRO, realizat de firma Borland este cel mai nou şi puternic produs din
categoria sa. El combină într-un mod fericit tot ceea ce este pozitiv la rivalii săi adăugând şi multe
facilităţi proprii.
EXCEL
Produsul firmei Microsoft, EXCEL este o aplicaţie care funcţionează sub Windows. De aici
rezultă în mod direct unele din caracteristicile sale (utilizare mai comodă, meniuri foarte clare şi
standardizate, funcţii grafice deosebit de puternice, viteză de lucru inferioară lui Quatro).
Câteva specificaţii tehnice pentru EXCEL ar fi:
 tabelă cu dimensiunea maximă de 1638 x 256 celule;
 lăţimea maximă a unei coloane este de 255 caractere;
 tabelele şi grafica pot exista pe foi distincte;
 funcţioneauă după principiul WYSIWYG;
 se pot folosi maxim 4 fonturi la un moment dat;
 limbaj de programare puternic şi flexibil;
 posibilitatea definirii de macroinstrucţiuni;
 nu posedă funcţie de salvare automată;
 conţine suport de funcţionare în reţea;
 detectează prezenţa coprocesorului matematic şi face uz de facilităţile acestuia;
 lucrează cu memoria expandată.
Alte limbaje orientate
Limbaje orientate pe calcul matematic simbolic
Specialiştii din domeniul cercetării matematice au la dispoziţie unelte de lucru extrem de utile
pentru eliminarea calculului matematic rutinier. În acest scop au fost create limbaje de programare care
pot recunoaşte şi rezolva formule sau ecuaţii matematice complexe. Expresiile manevrate pot conţine
operaţii algebrice elementare, operatori de derivare, de integrare, operatori diferenţiali care sunt
recunoscuţi de sistem ca atare. În plus sunt oferite instrucţiuni absolut necesare pentru a controla un
program.
Cele mai importante produse de acest gen sunt REDUCE, SYMNON, MATHCAD,
MATHEMATICA, MATHLAB.
Limbaje orientate pe programarea inteligenţei artificiale
Acest tip de limbaje diferă esenţial de cele algoritmice. Modalitatea de programare este
descriptivă şi are intenţia declarată de simulare a raţionamentului uman. Pentru rezolvarea unei probleme
sunt furnizate seturile de reguli şi informaţii necesare, iar apoi se descrie în ce constă problema ca atare.
Limbajul este capabil să opereze deducţiile (deciziile) necesare pentru a rezolva problema într-un caz
particular ce apare în practică.
Aşadar, aceste limbaje descriu problema de rezolvat (în termenii deducţiilor logice) pe când
limbajele de tip algoritmic descriu metoda de rezolvare a problemei. Domeniile de aplicabilitate pentru
limbajele de programare a inteligenţei artificiale sunt cu predilecţie: realizarea de sisteme expert
(programe ce înlocuiesc experţii umani), computerizarea procesului de producţie, robotică, tratarea
limbajelor naturale.
Cele mai importante limbaje de acest tip sunt:
 PROLOG (PROgramming in LOGic) creat în 1973 şi implementat pe PC-uri abia în
1986 de firma Borland sub forma Turbo-Prolog.
53

52.  LISP (LISt Processing language) conceput în 1976 şi implementat pe PC-uri de firma
Microsoft sub forma MuLISP.
GENERAŢII DE CALCULATOARE
Generaţia I (1946-1956) caracterizată prin:
 Hardware: relee, tuburi electronice;
 Software: programe cablate, cod maşină, limbaj de asamblare;
 Capacitate de memorie: 2 Kocteţi;
 Viteză de operare: 10.000 de operaţii/sec.;
 Calulatoare: ENIAC, UNIVAC, IBM;
Generaţia a II–a (1957-1963) marcată de apariţia tranzistorului
 Hardware: tranzistoare, memorii cu ferite, cablaj imprimat;
 Software: limbaj de nivel înalt ( Algol, Fortan)
 Memorie: 32 Kocteţi;
 Viteza: 200.000 de instrucţiuni/sec
 Calculatoare: IBM 7040, NCR501;
Generaţia a III–a (1964- 1981) caracterizată prin:
 Hardware: circuite integrate (la început pe scară redusă, apoi pe scară medie şi largă;
scara de integrare se referă la numărul de componente electronice pe unitatea de suprafaţă),
cablaje imprimate multistrat, discuri magnetice, aparariţia primelor microprocesoare;
 Software: limbaje de nivel foarte înalt, programare orientată pe obiecte B.Pascal,
programare structurată LISP, primele programe pentru grafică şi baze de date .
 Memorie: 1÷2 Mocteţi ;
 Viteza: 5.000.000 de operaţii/sec;
 Calculatoare: IBM 370, FELIX
 Comunicaţii: Primele comunicaţii prin satelit, transmisia de date prin fibră optică.
Generaţia a IV-a (1982-1989) caracterizată prin:
 Hardware: circuite integrate pe scară foarte mare (VLSI), sisteme distribuite de calcul,
apar microprocesoarele de 16/32 biţi, primele elemente optice (discurile optice);
 Software: Pachete de programe de largă utilizare, sisteme expert, sisteme de operare, se
perfecţioneaza limbajele de programare orientate pe obiect, baze de date relaţionale;
 Memorie: 8÷10 Mocteţi;
 Viteza: 30 de milioane de instrucţiuni/sec;
 Caculatoare: INDEPENDENT, CORAL, IBM (apar mai multe versiuni)
Generaţia a V-a (1991-2002) în curs de dezvolatare
 Hardware: circuite integrate pe scară ultralargă ULSI (proiectare circuite integrate 3D),
arhitecturi paralele, alte soluţii arhitecturale noi (reţele neurale etc.), proiectele galiu-arsen.
 Software: limbaje concurente, programare funcţională, prelucrare simbolică, baze de
cunoştiinţe, sisteme expert evoluate, programe de realitate virtuală, acum apar şi sistemele
de operare windows. Această perioadă este marcată de apariţia internetului şi extinderea
rapidă a acestei reţele mondiale.
 Memorie: de la zeci, sute de Mocteţi până la Gocteţi;
 Viteza: 1G de instrucţiuni /sec – 3 G de instrucţiuni/sec
 Comunicaţiile: au atins un nivel nemaiîntâlnit, emisiile radio de ordinul GHz, reţele
globale pe fibră optică, reţele de comunicare prin satelit.
 Calculatoare: o gamă foarte largă de calculatoare.
54

53. CAPITOLUL VII
LIMBAJUL VISUAL BASIC
7.1 Programarea aplicaţiilor Windows
Pentru realizarea unei aplicaţii pot fi avute în vedere două tehnologii de programare şi anume:
– programare procedurală
– programare orientată spre obiecte şi dirijată de evenimente.
În programarea procedurală, o aplicaţie este constituită din unul sau mai multe programe care se
vor executa într-o anumită ordine, fiecare program fiind constituit dintr-o secvenţă de instrucţuni scrise
într-un limbaj de programare.
Acesta era modul clasic de realizare a aplicaţiilor şi sistemelor informatice şi are o serie de
dezavantaje printre care: productivitate scăzută în realizarea programelor, efort mare pentru realizarea
programelor şi mai ales a interfeţelor etc.
Apariţia tehnologiei orientate obiect, a mediilor visuale de programare şi a sistemului de operare
Windows a condus la apariţia şi dezvoltarea unei noi tehnologii de programare a aplicaţiilor windows şi
anume programarea orientată pe obiecte şi dirijată de evenimente, tehnologie ce va fi prezentată în cele ce
urmează în cadrul limbajului Visual Basic.
O aplicaţie Windows afişează unul sau mai multe ecrane care conţin obiecte cu care va
interacţiona utilizatorul pentru a controla evoluţia programului. Într-un mediu de programare vizual,
obiectele principale sunt formele şi controalele desenate în forme (formă = o fereastră) Aceste obiecte pot
fi create prin selecţie şi depunere folosind barele de instrumente ale mediului respectiv.
Spre exemplu, bara cu instrumente Visual Basic permite crearea unei varietăţi de obiecte printre
care: forme, butoane, casete cu listă, casete derulante combinate, casete de validare, butoane radio
(butoane de opţiune), etc. Fiecare din aceste obiecte are un comportament predefinit. Spre exemplu când
se execută click pe un buton acesta trece în poziţia apăsat şi apoi revine în poziţia normală. Pentru a
schimba comportamentul obiectului acestuia trebuie să-i ataşaţi cod de program (instrucţiuni)
corespunzător, cod ce se va executa atunci când are loc un anumit eveniment (spre exemplu în cazul
butonului evenimentul este click).
Evenimentele se produc ca urmare a unei acţiuni a utilizatorului (ex. evenimentul click
corespunde apăsării butonului stâng al mouse-ului pe obiectul respectiv), sau în urma execuţiei codului
programului, sau pot fi declanşate de către sistem.
Majoritatea obiectelor vor răspunde unui anumit număr de evenimente generate de către utilizator
printre care click-uri, dublu click-uri, apăsări de taste sau trageri şi eliberări ale obiectului. Limbajul
Visual Basic pune la dispoziţia utilizatorului un mediu de dezvoltare care permite crearea de programe
orientate spre obiecte şi conduse de evenimente. Pentru lucrul cu obiecte conduse de evenimente se
parcurg următoarele etape:
– se creează o nouă formă căreia i se dă un nume;
– se desenează şi se denumesc obiectele ce urmează a fi afişate în forma respectivă;
– se ataşează fiecărui obiect codul ce va fi executat ca răspuns la evenimente generate de
utilizator sau de sistem.
Va rezulta o interfaţă grafică cu care interacţionează utilizatorul pentru a controla evoluţia
programului. Rezumând putem spune că în programarea orientată spre obiecte şi dirijată de evenimente,
obiectele au un comportament predefinit care poate fi modificat de utilizator prin ataşare de cod
corespunzător şi aceste obiecte răspund la evenimente declanşate fie ca urmare a acţiunii utilizatorului
asupra obiectelor, fie ca urmare a execuţiei codului ataşat, fie declanşate de sistem.
55

54. 7.2 Proprietăţi şi metode
Un obiect este definit de un set de proprietăţi cum ar fi: dimensiune, culoare, poziţie pe ecran,
comportament (ex. dacă un buton radio este activ sau nu la un moment dat etc.). O metodă este o
procedură (succesiune de instrucţiuni) asociată unei anumite acţiuni a unui obiect. Spre exemplu în Visual
Basic există o metodă Move asociată majorităţii obiectelor (permite mutarea obiectelor).
Deci proprietăţile descriu obiectele iar metodele definesc acţiunile obiectelor, iar pe de altă parte
proprietăţile reprezintă date iar metodele reprezintă cod (instrucţiuni). Astfel în gramatica programării
orientate spre obiecte :
– obiectele sunt substantive;
– proprietăţile sunt adjective;
– metodele sunt verbe.
Utilizarea notaţiei cu punct pentru referirea proprietăţilor şi metodelor
Referirea unei proprietăţi se face astfel:
Obiect . Proprietate = Valoare
Exemplu - fie forma frmForma1 şi variabila dColor în care memorăm culoarea de fond a formei
dColor = frmForma1.BackColor (citeşte culoarea curentă şi o depune în dColor)
frmForma1.BackColor = QBColor (Blue) – stabileşte noua culoare de fond a formei la valoarea
Blue.
Referirea metodelor se face asemănător cu referirea proprietăţilor, însă în plus metodele pot
necesita precizarea unor informaţii suplimentare.
Exemplu - pentru mutarea obiectului Buton1 în colţul din stânga sus al formei curente se apelează
metoda Move şi se precizează coordonatele colţului din stânga sus:
Buton1.Move 0,0
Stabilire proprietăţi şi executare metode
Proprietăţile unui obiect pot fi setate în faza de proiectare (atunci când se desenează sau se
modifică formele) utilizând fişa Properties a formei sau obiectului din formă (fişa este automat vizualizată
la selecţia obiectului respectiv: forma, buton, etc.). De asemenea fişa Properties poate fi vizualizată prin
click dreapta şi selecţie Properties.
Proprietăţile pot fi modificate şi prin program în momentul execuţiei formei, dacă codul de
program asociat conţine instrucţiuni care referă şi setează proprietăţi (ca în exemplul de mai sus în care
schimbăm culoarea fondului formei).
Spre deosebire de proprietăţi, metodele pot fi executate numai în momentul execuţiei programului
(eventual în momentul depanării programului utilizând facilitatea Debugger a programului Visual Basic).
Denumirea obiectelor
Orice obiect are proprietăţile:
Name - numele utilizat în scrierea codului
Capture - numele dat obiectului pentru a putea fi identificat de utilizator. Visal Basic dă
nume implicite obiectelor. Este indicat ca utilizatorul să dea nume obiectelor (Name) utilizând
următoarea convenţie:
– un prefix format din 3 litere mici (ex. frm pentru formă, cmd pentru buton de comandă,
etc.)
– un şir de caractere care identifică obiectul (ex. Forma1, Ecran1, Buton1, etc.).
În tabelul următor sunt prezentate convenţiile de denumire a obiectelor din Visual Basic:
Obiect Prefix Exemplu
Formă Frm frmForma1
Buton de comandă cmd, btn cmdButon, btnOK
Casetă de text Txt txtCaseta1
56

55. Obiect Prefix Exemplu
Bare de derulare
- orizontală hsb
- verticală vsb
Meniu Mnu mnuMeniuPrinc
Casetă de validare Chk
Casetă cu lista Lst
Cadru Fra
Imagine Img
Buton de opţiune (radio) Opt optBO1
7.3 Instrucţiunile VBA
Generalităţi
Există trei categorii de instrucţiuni Visual Basic:
 instrucţiuni de declarare (prezentate la declararea variabilelor) prin care se denumesc şi
se declară tipul pentru variabile, constante şi proceduri;
 instrucţiuni de atribuire (prezentate în continuare) prin care se atribuie valori
variabilelor sau constantelor;
 instrucţiuni executabile (prezentate în continuare) care iniţiază acţiuni: execută metode
sau proceduri, controlează fluxul execuţiei codului.
În mediul de dezvoltare VBA, sintaxa instrucţiunilor este verificată automat după ce se trece la
instrucţiunea următoare (prin Enter).
Continuarea instrucţiunilor
O instrucţiune poate să fie scrisă pe mai multe linii prin utilizarea caracterului de continuare a
liniei "_" precedat de un spaţiu. De exemplu, crearea prin program a unui tabel într-un document Word:
ActiveDocument.Tables.Add Range:=Selection.Range, _
NumRows:=3, _
NumColumns:= 3
unde, pe lângă continuarea liniilor se va remarca utilizarea argumentelor numite la apelul metodei
de adăugare a unui nou tabel la colecţia de tabele a documentului.
Două instrucţiuni pot fi scrise pe o aceeaşi linie dacă sunt separate cu caracterul ":".
Etichetarea liniilor
O linie poate fi identificată:
 printr-o etichetă: orice nume, care respectă regulile generale, care începe în prima
coloană a liniei şi se termină cu caracterul ":"
 printr-un număr: orice combinaţie de cifre, care începe în prima coloană a liniei şi este
unic în modulul respectiv.
Identificatorii de linii pot fi utilizaţi în instrucţiuni de control, desi codul astfel construit nu
respectă regulile programării structurate.
Comentarii
Textele explicative (necesare documentării codului) pot fi introduse pe linii separate sau în
continuarea liniei de cod.
O linie de comentariu începe cu un apostrof (') sau cu cuvântul Rem urmat de un spaţiu.
57

56. Comentariul de pe aceeaşi linie cu o instrucţiune se introduce printr-un apostrof urmat de
comentariu.
Operatori
În formarea expresiilor de diverse tipuri, operatorii sunt cei utilizaţi aproape general în limbajele
de programare de nivel înalt. Pentru fixarea termenilor şi notaţiilor sunt totuşi prezentaţi, pe categorii,
însoţiţi, acolo unde este cazul de scurte explicaţii.
Operatori aritmetici
Operator Semnificaţie Observaţii
^ Ridicarea la rezultatul este Double sau Variant(Double) cu excepţia: dacă
putere un operand este Null, rezultatul este tot Null
* Înmulţirea rezultatul este dat de cel "mai precis" factor, ordinea
crescătoare a "preciziei" fiind, pentru înmulţire, Byte, Integer,
Long, Single, Currency, Double şi Decimal. Dacă o expresie
este Null, rezultatul este Null. O expresie Empty este
considerată ca 0. Pentru excepţii se va studia Help –
*(operator).
/ Împărţirea rezultatul este, în general, Double sau Variant(Double). Dacă
o expresie este Null, rezultatul este Null. O expresie Empty
este considerată ca 0. Pentru excepţii se va studia Help – /
(operator).
Împărţirea înainte de împărţire, operanzii sunt rotunjiţi la Byte, Integer
întreagă sau Long. Rezultatul este Byte, Variant(Byte), Integer,
Variant (Integer), Long, sau Variant(Long). Dacă o expresie
este Null, rezultatul este Null. O expresie Empty este
considerată ca 0.
Mod Restul operanzii sunt rotunjiţi la întregi şi se obţine restul împărţirii.
împărţirii Rezultatul este Byte, Variant(Byte), Integer, Variant
(Integer), Long, sau Variant(Long). Dacă o expresie este Null,
rezultatul este Null. O expresie Empty este considerată ca 0.
+ Adunarea în general, operanzi numerici produc adunarea, iar operanzi
numerică sau şiruri produc concatenarea. În cazul numeric, rezultatul este
concatenarea de tipul cel "mai precis" al operanzilor, ordinea de "precizie"
şirurilor fiind pentru adunare şi scădere: Byte, Integer, Long, Single,
Double, Currency şi Decimal. Deoarece operanzii pot fi orice
expresie, pentru o informare completă (de exemplu operanzi
Variant) se va studia Help – +(operator).
- Scăderea sau operanzii pot fi doar numerici. Rezultatul este de tipul cel
inversarea "mai precis" al operanzilor, ordinea de "precizie" fiind pentru
semnului adunare şi scădere: Byte, Integer, Long, Single, Double,
Currency şi Decimal. Dacă o expresie este Null, rezultatul
este Null. O expresie Empty este considerată ca 0. Pentru
excepţii se va studia Help – -(operator).
58

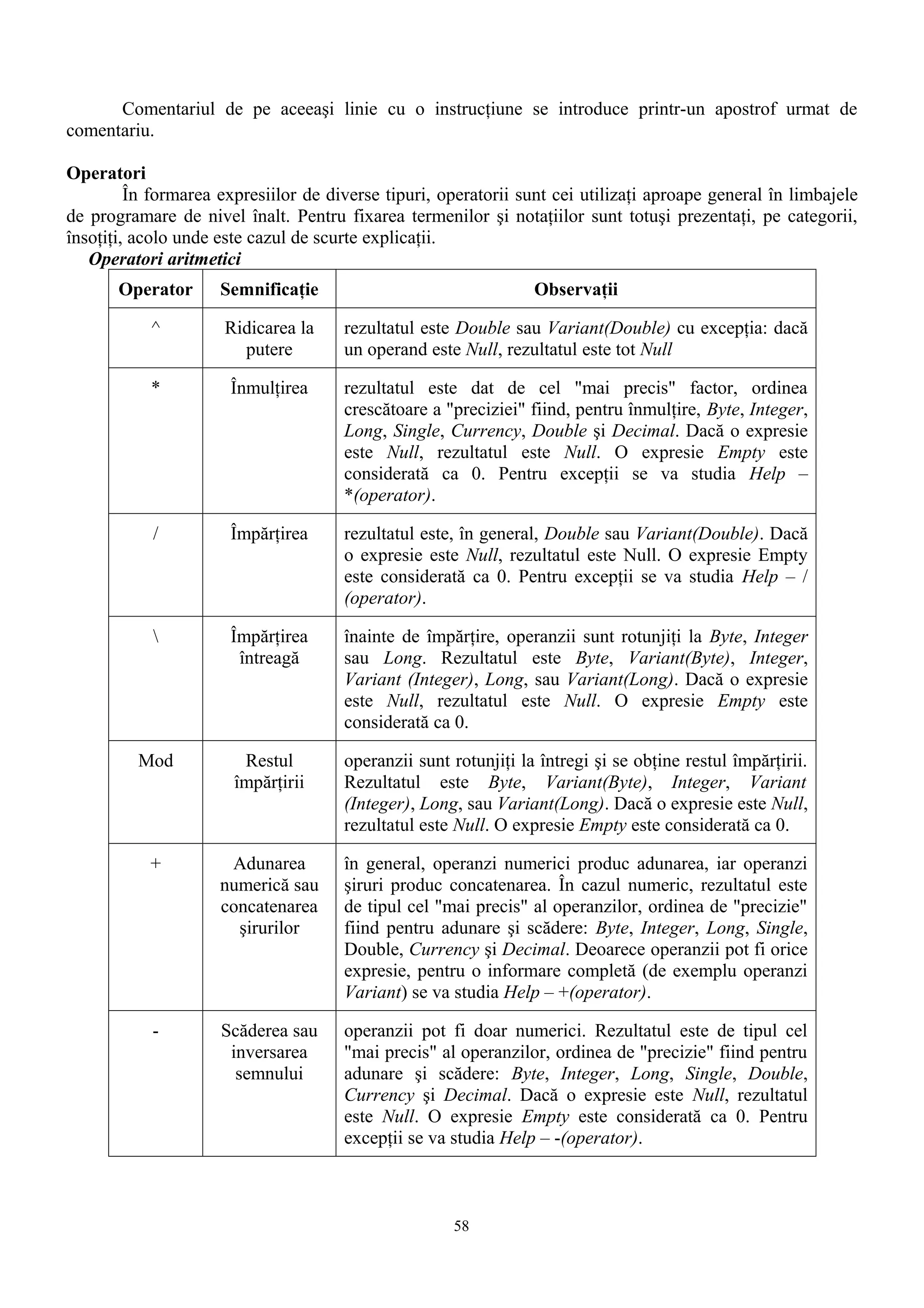
57. Operatori de comparare
Relaţiile care există între diferite tipuri de entităţi se pot evidenţia prin comparaţii având una
dintre formele următoare:
result = expression1 comparisonoperator expression2
result = object1 Is object2
result = string Like pattern
unde
result este o variabilă numerică
expression este o expresie oarecare
comparisonoperator este un operator relaţional
object este un nume de obiect
string este o expresie şir oarecare
pattern este o expresie String sau un domeniu de caractere.
Operatorii de comparare sunt cei uzuali: < (mai mic), <= (mai mic sau egal), > (mai mare), >=
(mai mare sau egal), = (egal), <> (diferit, neegal).
Rezultatul este True (dacă este adevărată relaţia), False (dacă relaţia este neadevărată), Null (dacă
cel puţin un operand este Null).
Operatorul Is produce True dacă variabilele se referă la acelaşi obiect şi False în caz contrar.
Operatorul Like compară două şiruri cu observaţia că al doilea tremen este un şablon. Prin urmare
rezultatul este True dacă primul şir operand este format după şablon, False în caz contrar. Atunci când un
operand este Null, rezultatul este tot Null.
Comportarea operatorului Like depinde de instrucţiunea Option Compare, care poate fi:
Option Compare Binary, ordinea este cea a reprezentării interne binare, determinată în
Windows de codul de pagină.
Option Compare Text, compararea este insenzitivă la capitalizarea textului, ordinea este
determinată de setările locale ale sistemului.
Construcţia şablonului poate cuprinde caractere wildcard, liste de caractere, domenii de caractere:
• un caracter oarecare
• oricâte caractere (chiar nici unul)
• # o cifră oarecare (0–9).
• [charlist] oricare dintre caracterele enumerate în listă, un domeniu de litere poate fi dat
prin utilizarea cratimei.
• [!charlist] orice caracter care nu este în listă
Observaţie. Pentru a utiliza în şablon caracterele speciale cu valoare de wildcard se vor utiliza construcţii
de tip listă: [[], [?] etc. Paranteza dreapta va fi indicată singură: ].
Pentru alte observaţii utile se va studia Help – Like operator.
Operatori de concatenare
Pentru combinarea şirurilor de caractere se pot utiliza operatorii & şi +.
În sintaxa
expression1 & expression2
unde operanzii sunt expresii oarecare, rezultatul este:
de tip String, dacă ambii operanzi sunt String
de tip Variant(String) în celelalte cazuri
Null, dacă ambii operanzi sunt Null.
Înainte de concatenare, operanzii care nu sunt şiruri se convertesc la Variant(String). Expresiile
Null sau Empty sunt tratate ca şiruri de lungime zero ("").
59

58. Operatori logici
Pentru operaţiile logice sunt utilizaţi următorii operatori, uzuali în programare.
Operator Semnificaţie Observaţii
And conjuncţia logică Null cu False dă False, Null cu True sau cu Null dă Null.
Operatorul And realizează şi operaţia de conjuncţie bit cu
bit pentru expresii numerice.
Eqv echivalenţa logică Dacă o expresie este Null, rezultatul este Null. Eqv
realizează şi compararea bit cu bit a două expresii
numerice, poziţionând cifrele binare ale rezultatului după
regulile de calcul ale echivalenţei logice: 0 Eqv 0 este 1
etc.
Imp implicaţia logică True Imp Null este Null, False Imp * este True, Null Imp
True este True, Null Imp False (sau Null) este Null.
Operatorul Imp realizează şi compararea bit cu bit a două
expresii numerice, poziţionând cifrele binare ale
rezultatului după regulile de calcul ale implicaţiei logice: 1
Imp 0 este 0, în rest rezultatul este 1.
Not negaţia logică Not Null este Null. Prin operatorul Not se poate inversa bit
cu bit valorile unei variabile, poziţionându-se
corespunzător un rezultat numeric.
Or disjuncţia logică Null Or True este True, Null cu False (sau Null) este Null.
Operatorul Or realizează şi o comparaţie bit cu bit a două
expresii numerice poziţionând biţii corespunzători ai
rezultatului după regulile lui Or logic.
Xor disjuncţia Dacă un operand este Null, atunci rezultatul este Null. Se
exclusivă poate efectua operaţia de sau exclusiv şi bit cu bit pentru
două expresii numerice [b1+b2(mod 2)].
Instrucţiuni de atribuire
Atribuirea se poate efectua prin instrucţiunea Let (pentru valori atribuite variabilelor şi
proprietăţilor), Set (pentru atribuirea de obiecte la o variabilă de tip obiect), Lset şi Rset (pentru atribuiri
speciale de şiruri sau tipuri definite de utilizator).
Instrucţiunea Let
Atribuie valoarea unei expresii la o variabilă sau proprietate.
[Let] varname = expression
unde varname este nume de variabilă sau de proprietate.
Este de remarcat forma posibilă (şi de fapt general utilizată) fără cuvântul Let.
Observaţii. Valoarea expresiei trebuie să fie compatibilă ca tip cu variabila (sau proprietatea): valori
numerice nu pot fi atribuite variabilelor de tip String şi nici reciproc.
Variabilele Variant pot primi valori numerice sau String, reciproc nu este valabil decât dacă
valoarea expresiei Variant poate fi interpretată compatibilă cu tipul variabilei: orice Variant poate fi
atribuit unei variabile de tip String (cu excepţia Null), doar Variant care poate fi interpretat nuric poate fi
atribuit unei variabile de tip numeric.
La atribuirea valorilor numerice pot avea loc conversii la tipul numeric al variabilei.
Atribuirea valorilor de tip utilizator poate fi efectuată doar dacă ambii termeni au acelaşi tip
definit. Pentru alte situaţii se va utiliza instrucţiunea Lset.
Nu se poate utiliza Let (cu sau fără cuvântul Let) pentru legarea de obiecte la variabile obiect. Se
va utiliza în această situaţie instrucţiunea Set.
60

59. Instrucţiunea LSet
Copie, cu aliniere la stânga, un şir de caractere (valoarea expresiei din dreapta) într-o variabila de
tip String. Deoarece copierea este binară, poate fi utilizată pentru atribuiri între tipuri utilizator diferite
(rezultatul este impredictibil deoarece nu se face nici o verificare de tipuri/componente ale valorilor de tip
record). Sintaxa este
LSet stringvar = string
LSet varname1 = varname2
unde
stringvar, string reprezintă variabila de tip String şi expresia de acelaşi tip implicate într-o
atribuire de şiruri.
varname1, varname2 sunt denumiri de variabile, de tipuri definite de utilizator (vezi
instrucţiunea Type) diferite. Zona de memorie alocată celei de a doua variabile este copiată
(aliniată la stânga) în zona de memorie a primei variabile.
Caracterele care rămân neocupate se completează cu spaţii, iar dacă zona de unde se copie este
mai mare, caracterele din dreapta se pierd (sunt trunchiate).
Instrucţiunea LSet
Copie, cu aliniere la dreapta, un şir de caractere (valoarea expresiei din dreapta) într-o variabila de
tip String. Sintaxa este
RSet stringvar = string
Caracterele rămase neocupate în variabilă sunt completate cu spaţii. Instrucţiunea RSet nu se
poate utiliza (analog lui LSet) pentru tipuri definite de utilizator.
Instrucţiuni executabile
Execuţia unui program are loc, în lipsa oricărui control, instrucţiune cu instrucţiune, de la stânga
la dreapta şi de sus în jos. Acest sens poate fi modificat, într-o oarecare măsură, prin ordinea de
precedenţă a operaţiilor în evaluarea expresiilor. Este evident că o asemenea structură simplă nu poate
cuprinde toate aspectele programării şi din acest motiv necesitatea structurilor de control a fluxului
execuţiei. Unele instrucţiuni au fost păstrate doar din motive de compatibilitate cu versiunile iniţiale ale
limbajului, în locul lor fiind preferate structuri mai evoluate sau similare altor limbaje de programare.
Instrucţiuni de transfer (GoSub…Return, GoTo, OnError, On…GoSub, On…GoTo)
Această categorie cuprinde instrucţiunile prin care controlul execuţiei este transferat la o altă
instrucţiune din procedură. În general, utilizarea acestor comenzi nu produce programe foarte structurate
(în sensul programării structurate) şi prin urmare, pentru o mai mare claritate a codului, pot fi înlocuite cu
alte structuri de programare.
GoSub…Return
În cadrul unei proceduri un grup de instrucţiuni poate fi organizat ca o subrutină (similar unei
proceduri on-line, nenumite) identificată prin linia de început. Transferul controlului la acest grup de
instrucţiuni şi revenirea la locul apelului se poate efectua prin GoSub…Return cu sintaxa
GoSub line
...
line
...
Return
unde line este o etichetă de linie sau un număr de linie din aceeaşi procedură.
Pot exista mai multe instrucţiuni Return, prima executată produce saltul la instrucţiunea care
urmează celei mai recente instrucţiuni GoSub executate.
61

60. GoTo
Realizează tranferul controlului execuţiei la o linie din aceeaşi procedură.
GoTo line
unde line este o etichetă de linie sau un număr de linie din aceeaşi procedură.
On Error
Permite controlul erorilor prin transferul controlului la rutine de tratare.
Observaţie. Este prezentată în secţiunea dedicată controlului erorilor.
On…GoSub, On…GoTo
Permit o ramificare multiplă, după valoarea unei expresii. Se recomandă, pentru claritatea codului,
utilizarea structurii Select Case în locul acestor structuri.
On expression GoSub destinationlist
On expression GoTo destinationlist
unde
expression este o expresie numerică având valoare întreagă (după o eventuală rotunjire)
între 0 şi 255 inclusiv.
destinationlist este o listă de etichete de linii sau numere de linii, separate prin virgule
(elementele pot fi de ambele categorii), din aceeaşi procedură cu instrucţiunea.
Dacă valoarea expresiei este negativă sau mai mare decât 255 se produce o eroare.
Dacă valoarea expresiei, fie ea k, este în domeniul rangurilor listei, atunci se transferă controlul la
linia identificată de al k-lea element al listei.
Dacă valoarea expresiei este 0 sau mai mare decât numărul de elemente din listă, transferul se
efectuează la linia care urmează instrucţiunea On...GoSub sau On...GoTo.
Instrucţiuni de terminare sau oprire a programului (DoEvents, End, Exit, Stop)
Terminarea execuţiei programului sau oprirea temporară (pauza) se pot realiza prin instrucţiunile
enumerate aici.
DoEvents
Deşi nu este o instrucţiune VBA ci este o funcţie, includerea ei este naturală prin aceea că permite
cedarea controlului către sistemul de operare, care poate astfel să funcţioneze în regim de multitasking.
Acţiunea poate fi realizată şi prin alte tehnici (de exemplu utilizarea unui Timer etc.). Sintaxa este
DoEvents( )
Funcţia returnează, în general, valoarea 0.
Controlul este redat programului după ce sistemul de operare a terminat procesarea evenimentelor
din coada de evenimente, ca şi procesarea tuturor caracterelor din coada SendKeys.
Observaţie. Pentru alte observaţii se va studia documentaţia comenzii DoEvents.
End
Termină execuţia unei proceduri (sub forma prezentată aici) sau indică sfârşitul codului unei
structuri de tip bloc (cum ar fi End Function, End If etc., prezentate la structurile respective).
Sintaxa, în ipostaza opririi execuţiei, este:
End
Prin această instrucţiune, care poate fi plasată oriunde în program, execuţia este terminată imediat,
fără a se mai executa eventualele instrucţiuni scrise pentru tratarea unor evenimente specifice sfârşitului
de program (Unload, Terminate etc.).
Fişierele deschise prin Open sunt închise şi toate variabilele sunt eliberate. Obiectele create din
modulele clasă sunt distruse, iar referinţele din alte aplicaţii la asemenea obiecte sunt invalidate. Memoria
este eliberată.
62

61. Exit
Prin instrucţiunea Exit, sub una din multiplele ei forme, se întrerupe o ramură de execuţie (cum ar
fi o procedură, o structură iterativă etc.) pentru a se continua nivelul apelant. Sintaxa este
Exit Do
Exit For
Exit Function
Exit Property
Exit Sub
şi efectele sunt prezentate la structurile respective. Nu trebuie confundată cu instrucţiunea End.
Stop
Efectul instrucţiunii este dependent de modul de execuţiei a programului. Dacă se execută varianta
compilată a programului (fişierul .exe) atunci instrucţiunea este similară instrucţiunii End (suspendă
execuţia şi închide fişierele deschise). Dacă execuţia este din mediul VBA, atunci se suspendă execuţia
programului, dar nu se închid fişierele deschise şi nu se şterge valoarea variabilelor. Execuţia poate fi
reluată din punctul de suspendare.
Stop
Instrucţiunea este similară introducerii unui punct de oprire (Breakpoint) în codul sursă.
Structuri iterative (Do...Loop, For...Next, For Each...Next, While...Wend, With)
Prin intermediul construcţiilor de tip bloc prezentate în această secţiune se poate repeta, în mod
controlat, un grup de instrucţiuni. În cazul unui număr nedefinit de repetiţii, condiţia de oprire poate fi
testată la începutul sau la sfârşitul unui ciclu, prin alegerea structurii adecvate.
Do…Loop
Se vor utiliza structuri Do…Loop pentru a executa un grup de instrucţiuni de un număr de ori
nedefinit aprioric. Dacă se cunoaşte numărul de cicluri, se va utiliza structura For…Next.
Înainte de continuare se va testa o condiţie (despre care se presupune că poate fi modificată în
instrucţiunile executate). Diferitele variante posibile pentru Do…Loop diferă după momentul evaluării
condiţiei şi decizia luată.
Do [{While | Until} condition]
[statements]
[Exit Do]
[statements]
Loop
sau
Do
[statements]
[Exit Do]
[statements]
Loop [{While | Until} condition]
unde
condition este o expresie care valoare de adevăr True sau False. O condiţie care este Null
se consideră False.
statements sunt instrucţiounile care se repetă atâta timp (while) sau până când (until)
condiţia devine True.
Dacă decizia este de a nu continua ciclarea, atunci se va executa prima instrucţiune care urmează
întregii structuri (deci de după linia care începe cu Loop).
Se poate abandona ciclarea oriunde în corpul structurii prin utilizarea comenzii Exit Do (cu
această sintaxă). Dacă apare o comandă Exit Do se poate omite chiar şi condiţia din enunţ întrucât
execuţia se va termina prin această decizie.
63

62. Structurile Do pot fi inserate (dar complet) unele în altele. O terminare (prin orice metodă) a unei
bucle transferă controlul la nivelul Do imediat superior.
Execuţia structurilor este explicată în tabelul următor
Do While…Loop Testează condiţia la începutul buclei, execută bucla
numai dacă rezultatul este True şi continuă astfel
până când o nouă evaluare produce False.
Do Until…Loop Testează condiţia la începutul buclei, execută bucla
numai dacă rezultatul este False şi continuă astfel
până când o nouă evaluare produce True.
Do…Loop While Se execută întotdeauna bucla o dată, se testează
condiţia la sfârşitul buclei şi se repetă bucla atât
timp cât condiţia este True. Oprirea este pe
condiţie falsă.
Do…Loop Until Se execută întotdeauna bucla o dată, se testează
condiţia la sfârşitul buclei şi se repetă bucla atât
timp cât condiţia este False. Oprirea este pe
condiţie adevărată.
For…Next
Atunci când se cunoaşte numărul de repetări ale unui bloc de instrucţiuni, se va folosi structura
For…Next. Structura utilizează o variabilă contor, a cărei valoare se modifică la fiecare ciclu, oprirea
fiind atunci când se atinge o valoare specificată. Sintaxa este:
For counter = start To end [Step step]
[statements]
[Exit For]
[statements]
Next [counter]
unde
counter este variabila contor (numără repetările), de tip numeric. Nu poate fi de tip
Boolean sau element de tablou.
start este valoarea iniţială a contorului.
end este valoarea finală a contorului.
step este cantitatea care se adună la contor la fiecare pas. În cazul în care nu se specifică
este implicit 1. Poate fi şi negativă.
statements sunt instrucţiunile care se repetă. Dacă nu se specifică, atunci singura acţiune
este cea de modificare a contorului de un număr specificat de ori.
Acţiunea este dictată de pasul de incrementare şi relaţia dintre valoarea iniţială şi cea finală.
Instrucţiunile din corpul structurii se execută dacă
counter <= end pentru step >= 0 sau
counter >= end pentru step < 0.
După ce toate instrucţiunile s-au executat, valoarea step este adăugată la valoarea contorului şi
instrucţiunile se execută din nou după acelaşi test ca şi prima dată, sau bucla For…Next este terminată şi
se execută prima instrucţiune de după linia Next.
Specificarea numelui contorului în linia Next poate clarifica textul sursă, mai ales în cazul când
există structuri For…Next îmbricate.
Corpul unei bucle For…Next poate include (complet) o altă structură For…Next. În asemenea
situaţii, structurile îmbricate trebuie să aibă variabile contor diferite.
64

63. Instrucţiunile Exit For pot fi plasate oriunde în corpul unei bucle şi provoacă abandonarea ciclării.
Controlul execuţiei se transferă la prima instrucţiune de după linia Next.
For Each…Next
Similară structurii For…Next, structura For Each…Next repetă un grup de instrucţiuni pentru
fiecare element dintr-o colecţie de obiecte sau dintr-un tablou (cu excepţia celor de un tip utilizator). Este
utilă atunci când nu se cunoaşte numărul de elemente sau dacă se modifică, în timpul execuţiei, conţinutul
colecţiei.
Sintaxa este:
For Each element In group
[statements]
[Exit For]
[statements]
Next [element]
unde
element este variabila utilizată pentru parcurgerea elementelor. Dacă se parcurge o colecţie
de obiecte, atunci element poate fi Variant, o variabilă generică de tip Object, sau o
variabilă obiect specifică pentru biblioteca de obiecte referită. Pentru parcurgerea unui
tablou, element poate fi doar o variabilă de tip Variant.
group este numele colecţiei de obiecte sau al tabloului.
statements este grupul de istrucţiuni executate pentru fiecare element.
Execuţia unei structuri For Each…Next este:
Se defineşte element ca numind primul element din grup (dacă nu există nici un element, se
transferă controlul la prima instrucţiune de după Next – se părăseşte bucla fără executarea
instrucţiunilor).
Se execută instrucţiunile din corpul buclei For.
Se testează dacă element este ultimul element din grup. Dacă răspunsul este afirmatif, se
părăseşte bucla.
Se defineşte element ca numind următorul element din grup.
Se repetă paşii 2 până la 4.
Instrucţiunile Exit For sunt explicate la For…Next.
Buclele ForEach...Next pot fi îmbricate cu condiţia ca elementele utilizate la iterare să fie diferite.
Observaţie. Pentru ştergerea tuturor obiectelor dintr-o colecţie se va utiliza For…Next şi nu For Each…
Next. Se va utiliza ca număr de obiecte colecţie.Count.
While…Wend
Execută un grup de instrucţiuni atât timp cât este adevărată o condiţie. Sintaxa
While condition
[statements]
Wend
Este recomandat să se utilizeze o structură Do…Loop în locul acestei structuri.
With
Programarea orientată pe obiecte produce, datorită calificărilor succesive, construcţii foarte
complexe atunci când se numesc proprietăţile unui obiect. În cazul modificărilor succesive ale mai multor
proprietăţi ale aceluiaşi obiect, repetarea zonei de calificare poate produce erori de scriere şi conduce la
un text greu de citit. Codul este simplificat prin utilizarea structurii With…End With. O asemenea
structură execută o serie de instrucţiuni pentru un obiect sau pentru o variabilă de tip utilizator. Sintaxa
este:
With object
[statements]
65

64. End With
unde
object este numele unui obiect sau a unui tip definit de utilizator
statements sunt instrucţiunile care se execută pentru entitatea precizată.
Permiţând omiterea recalificărilor din referinţele la obiectul precizat, orice construcţie de tipul
".nume" este interpretată în instrucţiunile structurii drept "object.nume".
Într-un bloc With nu se poate schimba obiectul procesat.
La plasarea unui bloc With în interiorul altui bloc With, obiectul extern este mascat complet, deci
calificările eventuale la acest obiect vor fi efectuate.
Nu se recomandă saltul în şi dintr-un bloc With.
Structuri de decizie (If…Then…Else, Select Case)
Ramificarea firului execuţiei după rezultatul verificării unei condiţii este o necesitate frecventă în
orice implementare.
Pe lângă structurile prezentate, se pot utiliza trei funcţii care realizează alegeri în mod liniarizat
(pe o linie de cod): Choose(), Iif(), Switch().
If…Then…Else
O asemenea structură, întâlnită de altfel în toate limbajele de programare, execută un grup de
instrucţiuni ca răspuns la îndeplinirea unei condiţii (compusă sau nu din mai multe condiţii testate
secvenţial). Sintaxa permite o mare varietate de forme:
If condition Then [statements] [Else elsestatements]
sau
If condition Then
[statements]
[ElseIf condition-n Then
[elseifstatements] ...
[Else
[elsestatements]]
End If
unde
condition are una din formele: expresie numerică sau şir care se poate evalua True sau
False (Null este interpretat False);
expresie de forma TypeOf objectname Is objecttype, evaluată True dacă objectname este
de tipul obiect specificat în objecttype.
statements, elsestatements, elseifstatements sunt blocurile de instrucţiuni executate atunci
când condiţiile corespunzătoare sunt True.
La utilizarea primei forme, fără clauza Else, este posibil să se scrie mai multe instrucţiuni,
separate de ":", pe aceeaşi linie.
Verificarea condiţiilor implică evaluarea tuturor subexpresiilor, chiar dacă prin jocul operanzilor
şi operatorilor rezultatul poate fi precizat mai înainte (de exemplu OR cu primul operand True).
Select Case
Instrucţiunea Select Case se poate utiliza în locul unor instrucţiuni ElseIf multiple (dintr-o
structură If…Then…ElseIf) atunci când se compară aceeaşi expresie cu mai multe valori, diferite între
ele. Instrucţiunea Select Case furnizează, prin urmare, un sistem de luare a deciziilor similar instrucţiunii
If…Then…ElseIf. Totuşi, Select Case produce un un cod mai eficient şi mai inteligibil. Sintaxa este:
Select Case testexpression
[Case expressionlist-n
[statements-n]] ...
[Case Else
[elsestatements]]
66

65. End Select
unde
testexpression este o expresie numerică sau şir.
expressionlist-n este lista, separată prin virgule, a uneia sau mai multe expresii de forma:
expression.
expression To expression. Cuvântul To introduce un interval de valori, valoarea minimă
fiind prima specificată.
Is comparisonoperator expression. Se va utiliza Is cu operatori de comparare (exceptând
Is şi Like) pentru a specifica un domeniu de valori.
statements-n reprezintă una sau mai multe instrucţiuni care se vor executa dacă
testexpression este egală cu un element din expressionlist-n.
elsestatements reprezintă una sau mai multe instrucţiuni care se vor executa dacă
testexpression nu este egală cu nici un element din listele liniilor Case.
Dacă testexpression se potriveşte cu un element dintr-o listă Case, se vor executa instrucţiunile
care urmează această clauză Case până la următoarea clauză Case, sau până la End Select. Control
execuţiei trece apoi la instrucţiunea care urmează liniei finale End Select. Rezultă că dacă testexpression
se regăseşte în mai multe liste, doar prima potrivire este considerată.
Clauza Case Else are semnificaţia uzuală "altfel, în rest, în caz contrar etc.", adică introduce
instrucţiunile care se execută atunci când expresia de test nu se potriveşte nici unui element din listele
clauzelor Else. Dacă aceasta este situaţia şi nu este specificată o clauză Case Else, atunci execuţia
urmează cu prima instrucţiune de după End Select.
Instrucţiunile Select Case pot fi scufundate unele în altele, structurile interioare fiind complete
(fiecare structură are End Select propriu, includerea este completă).
Apeluri de proceduri şi programe
În această secţiune se prezintă doar funcţia Shell(), deoarece despre proceduri şi apelul lor s-a
discutat în capitolul 1.
Funcţia Shell()
Execută un program executabil şi returnează un Variant(Double) reprezentând ID-ul de task al
programului în caz de succes; în caz contrar returnează zero. Sintaxa este
Shell(pathname[,windowstyle])
unde
pathname este Variant (String). Conţine numele programului care se execută, argumentele
necesare şi poate da calea completă (dacă este nevoie).
windowstyle este Variant (Integer) şi precizează stilul ferestrei în care se va executa
programul (implicit este minimizat, cu focus).
Valorile posibile pentru argumentul windowstyle sunt
Constanta numită Valoarea Semnificaţia
VbHide 0 Fereastra este ascunsă iar focus-ul este pe fereastra ascunsă.
VbNormalFocus 1 Fereastra are focus-ul şi este dimensionată şi poziţionată normal.
VbMinimizedFocus 2 Fereastra este afişată ca o icoană (minimizată) dar are focus-ul.
VbMaximizedFocus 3 Fereastră maximizată, cu focus.
VbNormalNoFocus 4 Fereastra este normală (restaurată la mărimea şi poziţia cea mai recentă)
dar nu are focus-ul. Fereastra activă curentă îşi păstrează focus-ul.
VbMinimizedNoFocu 6 Fereastră minimizată, fără focus. Fereastra activă curentă îşi păstrează
s focus-ul.
67

66. Dacă funcţia Shell nu poate porni programul specificat se va semnala eroare. Programul pornit
prin Shell se execută asincron, deci nu există certitudinea că acest program se termină înainte de execuţia
instrucţiunilor care urmează liniei Shell.
68

67. CAPITOLUL VIII
REGULI IMPORTANTE PRIVIND ALEGEREA UNUI LIMBAJ DE PROGRAMARE
Prezentăm în continuare mai multe reguli importante, majoritatea dintre ele prezente şi explicate
în secţiunile anterioare.
1. Defineşte complet problema.
Această indicaţie, foarte importantă în activitatea de programare, pare fără sens pentru unii cititori.
Dar nu se poate rezolva o problemă dacă nu se cunoaşte această problemă. Specificarea corectă şi
completă a problemei nu este o sarcină trivială, ci una foarte importantă şi adeseori chiar dificilă.
Programul trebuie să respecte această specificaţie, să fie construit având tot timpul în faţă această
specificaţie, să i se demonstreze corectitudinea în raport cu această specificaţie, să fie testat şi validat
ţinând seama de această specificaţie.
2. Gândeşte mai întâi, programează pe urmă.
Începând cu scrierea specificaţiilor problemei, trebuie pusă în prim plan gândirea. Este specificaţia
problemei corectă? Între metodele de rezolvare posibile, care ar fi cea mai potrivită scopului urmărit? În
paralel cu proiectarea algoritmului demonstrează corectitudinea lui. Verifică corectitudinea fiecărui pas
înainte de a merge mai departe.
3. Nu folosi variabile neiniţializate.
Este vorba de prezenţa unei variabile într-o expresie fără ca în prealabil această variabilă să fi
primit valoare. Este o eroare foarte frecventă a programatorilor începători (dar nu numai a lor). Destule
compilatoare permit folosirea variabilelor neiniţializate, neverificând dacă o variabilă a fost iniţializată
înaintea folosirii ei. Alte compilatoare iniţializează automat variabilele numerice cu valoarea zero. Cu
toate acestea nu e bine să ne bazăm pe o asemenea iniţializare ci să atribuim singuri valorile iniţiale
corespunzătoare variabilelor. Programul realizat trebuie să fie portabil, să nu se bazeze pe specificul unui
anumit compilator.
4. Verifică valoarea variabilei imediat după obţinerea acesteia.
Dacă o variabilă întreagă trebuie să ia valori într-un subdomeniu c 1..c2 verifică respectarea acestei
proprietăţi. Orice încălcare a ei indică o eroare care trebuie înlăturată. Valoarea variabilei poate fi
calculată sau introdusă de utilizator. În primul caz, verificarea trebuie făcută după calcul, în al doilea caz
se recomandă ca verificarea să urmeze imediat după citirea valorii respectivei variabile.
5. Cunoaşte şi foloseşte metodele de programare.
Este vorba de programarea Top-Down, Rafinarea în paşi succesivi, Divide et impera [Gries85]),
Bottom-up şi mixtă, programarea modulară, programarea structurată şi celelalte metode prezentate în
acest curs, sau alte metode ce vor fi asimilate ulterior.
Aceste metode încurajează reutilizarea, reducând costul realizării programelor. De asemenea,
folosirea unor componente existente (deci testate) măreşte gradul de fiabilitate a produselor soft realizate
şi scurtează perioada de realizare a acestora. Evident, dacă o parte din SUBPROGRAMii necesari
programului sunt deja scrişi şi verificaţi, viteza de lucru va creşte prin folosirea lor. Foloseşte deci
bibliotecile de componente reutilizabile existente şi construieşte singur astfel de biblioteci, care să
înglobeze experienţa proprie.
69

68. O bună programare modulară elimină legăturile între două module prin variabile globale. Se
recomandă ca fiecare modul să realizeze o activitate bine definită şi independentă de alt modul.
Comunicarea între două module trebuie să se realizeze numai prin mecanismul parametrilor formali-
actuali.
6. Amână pe mai târziu detaliile nesemnificative.
Această regulă stabileşte priorităţile de realizare a componentelor unui program; în primul rând se
acordă atenţie aspectelor esenţiale, începând cu modulul principal. În fiecare fază dă atenţie lucrurilor
importante. De exemplu, este inutil să se piardă timp cu scrierea unor părţi de program pentru tipărirea
rezultatelor şi a constata ulterior că rezultatele nu sunt cele dorite, sau nu sunt corecte.
Nu uita însă că pentru beneficiar "Detaliile nesemnificative sunt semnificative". Beneficiarii ţin
foarte mult la forma rezultatelor şi, adeseori, judecă programatorii după această formă. E păcat de munca
depusă dacă tipărirea rezultatelor lasă o impresie proastă asupra beneficiarului.
7. Evită artificiile.
Prin folosirea artificiilor în programare, a prescurtărilor şi simplificărilor se pierde adesea din
claritatea programului şi, mult mai grav, uneori se ajunge chiar la introducerea unor erori. În plus se poate
pierde portabilitatea programului.
Există însă situaţii în care prin anumite artificii se câştigă eficienţă în execuţie sau se face
economie de memorie. Dacă acest fapt este important atunci artificiile sunt binevenite, în caz contrar nu
se recomandă folosirea lor.
8. Foloseşte constante simbolice.
Folosirea intensivă a constantelor simbolice este recomandată oriunde în textul sursă trebuie scris
un număr (la declararea tablourilor, la precizarea limitelor de variaţie a unor variabile, etc.). Prin
utilizarea acestor constante se măreşte gradul de generalitate a textului scris, iar în situaţia în care
valoarea unei constante trebuie schimbată, modificarea este mult mai uşoară (doar la locul definiţiei
constantei) şi nu duce la erori. Ea implică numai definiţia constantei, nu modificarea valorii concrete în
toate instrucţiunile programului.
9. Verifică corectitudinea algoritmului şi programului în fiecare etapă a elaborării lor.
Detectarea şi eliminarea unei erori imediat după comiterea ei duce la creşterea vitezei de realizare
a produsului, evitându-se activităţi inutile de depanare. Se recomandă demonstrarea corectitudinii fiecărui
algoritm folosit, întrucât erorile semnalate în timpul testării sunt adeseori greu de descoperit şi, câteodată,
imposibil de eliminat altfel decât prin rescrierea modulului sau programului respectiv. Urmează testarea
fiecărui subprogram imediat după ce a fost scris (codificat). Acest lucru se potriveşte codificării bottom-
up şi sugerează o abordare sistematică a activităţii de codificare. Dacă pentru proiectare se pot folosi
oricare dintre metodele indicate, în codificare (şi testarea aferentă codificării), abordarea de jos în sus este
esenţială. Sugerăm ca această testare să se facă independent de programul în care se va folosi
subprogramul testat. Este adevărat că activitatea de testare necesită un anumit timp, dar ea este utilă cel
puţin din trei puncte de vedere:
– scoate în evidenţă erorile provocate de proiectarea algoritmului sau codificarea
neadecvată a acestuia;
– facilitează detectarea erorilor, deoarece dimensiunea problemei este mai mică; în fapt nu
se pierde timp cu scrierea unui program de test, ci se câştigă timp, deoarece la fiecare nivel
de detaliere se vor folosi numai componente testate deja; ceea ce rămâne de testat la
nivelul respectiv este gestiunea corectă a apelurilor respectivelor componente;
70

69. – obligă implementatorul să gândească încă o utilizare (cel puţin) a respectivului
subprogram, independentă de cea pentru care a fost iniţial conceput.
10. Foloseşte denumiri sugestive pentru identificatorii utilizaţi în program.
Fiecare identificator (nume de variabilă, de tip de date, de constante, de subprograme) îşi are rolul
şi semnificaţia lui într-un program. E bine ca denumirea să reflecte această semnificaţie, mărind astfel
claritatea textului programului.
Unii programatori exagerează însă, folosind identificatori lungi, obţinuţi prin concatenarea mai
multor cuvinte. E clar că denumirea alesă redă semnificaţia variabilei, dar claritatea textului scade,
lungimea programului creşte şi citirea lui devine greoaie.
11. Cunoaşte şi respectă semnificaţia fiecărei variabile.
Fiecare variabilă are o semnificaţie. În demonstrarea corectitudinii algoritmului această
semnificaţie se reflectă, de cele mai multe ori, printr-un predicat invariant. O greşeală frecventă făcută de
unii programatori constă în folosirea unei variabile în mai multe scopuri.
12. Foloseşte variabile auxiliare numai acolo unde este strict necesar.
Fiecare variabilă trebuie să aibă o semnificaţie proprie, iar în demonstrarea corectitudinii
programului, acesteia i se ataşează un invariant, care trebuie verificat.
Folosirea necontrolată a mai multor variabile auxiliare, ruperea unor expresii chiar lungi în
subexpresii cu diferite denumiri, pot duce la reducerea clarităţii programului.
13. Prin scriere redă cât mai fidel structura programului.
Importanţa indentării şi spaţierii pentru claritatea programului au fost arătate anterior. Fiecare
programator trebuie să aibă propriile reguli de scriere, care să scoată cât mai bine în evidenţă structura
programului şi funcţiile fiecărei părţi a acestuia.
14. Nu uita să testezi programul chiar dacă ai demonstrat corectitudinea lui.
Sunt cunoscute demonstraţii greşite pentru unele teoreme celebre din matematică. Şi o
demonstraţie a corectitudinii unui program poate fi greşită. Dar, chiar dacă demonstrarea corectitudinii
algoritmului este validă, programul poate conţine greşeli de codificare, de introducere (tastare) sau pot fi
alte cauze care generează erori.
15. Nu recalcula limitele şi nu modifica variabila de ciclare în interiorul unei structuri repetitive
dată prin propoziţia Pseudocod PENTRU.
O astfel de practică poate duce la erori greu de detectat şi încalcă regulile programării structurate.
Atunci când este necesară schimbarea variabilei de ciclare sau a limitelor se recomandă folosirea uneia
din structurile repetitive REPETĂ sau CÂTTIMP.
16. Nu ieşi forţat din corpul unei structuri repetitive redată prin propoziţia Pseudocod PENTRU.
Instrucţiunea Pseudocod PENTRU corespunde unui număr cunoscut de execuţii ale corpului
ciclului. În situaţia când corpul conţine şi testarea condiţiei de continuare a ciclării, recomandăm a se
folosi structurile REPETĂ sau CÂTTIMP şi nu PENTRU.
71

70. 17. Elaborează documentaţia programului în paralel cu realizarea lui.
Aşa cum s-a arătat în mai multe locuri din acest material, pe durata de viaţă a unui program se iau
mai multe decizii. E bine ca aceste decizii să rămână consemnate împreună cu rezultatul final al fiecărei
faze din viaţa programului (specificarea problemei, proiectarea algoritmilor, programul propriu-zis, datele
de test folosite). Vor rezulta documentaţii de analiză, proiectare, implementare şi exploatare. Primele trei
sunt necesare la întreţinerea aplicaţiei, trebuind a fi actualizate ori de câte ori se produc modificări, iar
ultima este necesară celor care exploatează aplicaţia. Pe lângă acestea, un program bun va trebui să
posede şi o componentă de asistenţă on-line (funcţie help), care contribuie la asigurarea a ceea ce am
numit interfaţă prietenoasă.
18. Foloseşte comentariile.
Rolul comentariilor a fost explicat în secţiunea 4.4. Este foarte greu să descifrăm un program lipsit
de comentarii, chiar dacă este vorba de propriu; program scris în urmă cu câteva luni sau ani de zile.
Orice program sau modul trebuie să fie însoţit de comentarii explicative dacă dorim să-l refolosim şi nu
trebuie să scriem programe care să nu poată fi refolosite. Minimum de comentarii într-un modul trebuie să
conţină specificarea acestui modul şi semnificaţia fiecărei variabile.
72

71. CAPITOLUL IX
METODA BACKTRACKING
La dispoziţia celor care rezolvă probleme cu ajutorul calculatorului există mai multe metode.
Dintre acestea cel mai des utilizate sunt:
– metoda Greedy;
– metoda Divide et impera;
– metoda Branch and Bound;
– metoda Backtracking;
Metoda backtracking se aplică problemelor în care soluţia poate fi reprezentată sub forma unui
vector – x = (x1, x2, x3, …xk,… xn) € S, unde S este mulţimea soluţiilor problemei şi S = S1 x S2 x… x
Sn, şi Si sunt mulţimi finite având s elemente si xi € si , (¥)i = 1..n.
Pentru fiecare problemă se dau relaţii între componentele vectorului x, care sunt numite condiţii
interne; soluţiile posibile care satisfac condiţiile interne se numesc soluţii rezultat. Metoda de generare a
tuturor soluţiilor posibile si apoi de determinare a soluţiilor rezultat prin verificarea îndeplinirii condiţiilor
interne necesită foarte mult timp.
Metoda backtracking evită această generare şi este mai eficientă. Elementele vectorului x,
primesc pe rând valori în ordinea crescătoare a indicilor, x[k] va primi o valoare numai daca au fost
atribuite valori elementelor x1.. x[k-1]. La atribuirea valorii lui x[k] se verifica îndeplinirea unor condiţii
de continuare referitoare la x1…x[k-1]. Daca aceste condiţii nu sunt îndeplinite, la pasul k, acest lucru
înseamnă ca orice valori i-am atribui lui x[k+1], x[k+1], .. x[n] nu se va ajunge la o soluţie rezultat.
Metoda backtracking construieşte un vector soluţie în mod progresiv începând cu prima
componentă a vectorului şi mergând spre ultima cu eventuale reveniri asupra atribuirilor anterioare.
Metoda se aplica astfel :
1) se alege prima valoare sin S1 si I se atribuie lui x1 ;
2) se presupun generate elementele x1…x[k-1], cu valori din S1..S[k-1]; pentru generarea lui x[k] se
alege primul element din S[k] disponibil si pentru valoarea aleasa se testează îndeplinirea
condiţiilor de continuare.
Pot apărea următoarele situaţii :
a) x[k] îndeplineşte condiţiile de continuare. Daca s-a ajuns la soluţia finală (k = n) atunci se
afişează soluţia obţinută. Daca nu s-a ajuns la soluţia finală se trece la generarea
elementului următor – x [k-1];
b) x[k] nu îndeplineşte condiţiile de continuare. Se încearcă următoarea valoare disponibila
din S[k]. Daca nu se găseşte nici o valoare în S[k] care să îndeplinească condiţiile de
continuare, se revine la elementul x[k-1] şi se reia algoritmul pentru o nouă valoare a
acestuia. Algoritmul se încheie când au fost luate in considerare toate elementele lui S1.
Problemele rezolvate prin această metodă necesită timp mare de execuţie, de aceea este indicat sa
se folosească metoda numai daca nu avem alt algoritm de rezolvare.
Dacă mulţimile S1,S2,…Sn au acelaşi număr k de elemente, timpul necesar de execuţie al
algoritmului este k la n. Dacă mulţimile S1, S2.. Sn nu au acelaşi număr de elemente, atunci se notează cu
„m” minimul cardinalelor mulţimilor S1…Sn si cu „M”, maximul. Timpul de execuţie este situat în
intervalul [m la n .. M la n]. Metoda backtracking are complexitatea exponenţială, in cele mai multe
cazuri fiind ineficientă. Ea insa nu poate fi înlocuită cu alte variante de rezolvare mai rapide în situaţia în
care se cere determinarea tuturor soluţiilor unei probleme.
Generarea permutărilor. Se citeşte un număr natural n. Să se genereze toate permutările
mulţimii {1, 2, 3, …,n}.
Generarea permutărilor se va face ţinând cont că orice permutare va fi alcătuită din elemente
distincte ale mulţimii A. Din acest motiv, la generarea unei permutări, vom urmări ca numerele să fie
distincte.
73

72. Prezentăm algoritmul corespunzător cazului n=3:
1 2 3
1 2 2 2 2
1 1 1 1 1 1
1 2 3
3 3 3 3 1
1 1 1 1 2 2
1 2 3 1
1 1 1 2 3 3
2 2 2 2 2 2
 se încarcă în stivă pe nivelul 1 valoarea 1;
 încărcarea valorii 1 pe nivelul al 2-lea nu este posibilă, întrucât această valoare se
găseşte şi pe nivelul 1 al stivei;
 încărcarea valorii 2 pe nivelul al 2-lea este posibilă, deoarece această valoare nu mai
este întâlnită;
 valoarea 1 din nivelul al 3-lea se regăseşte pe nivelul 1;
 valoarea 2 din nivelul al 3-lea se regăseşte pe nivelul al 2-lea;
 valoarea 3 pe nivelul al 3-lea nu e întâlnită pe nivelurile anterioare; întrucât nivelul 3
este completat corect. Tipărim: 1 2 3
……
Algoritmul continuă până când stiva devine vidă.
Programul sursa este urmatorul:
Private Sub CommandButton14_Click()
cit_n "n = ", n
back_perm
End Sub
Sub back_perm()
Dim k As Integer
k = 1
While k > 0
Do
succesor am_suc, st, k
If am_suc = True Then
valid1 ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tipar_r
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
74

73. End Sub
Sub valid1(ev As Boolean, st As stiva, k As Integer)
ev = True
For i = 1 To k - 1
If (st.ss(i) = st.ss(k)) Then
ev = False
End If
Next
End Sub
Sub tipar_r()
Dim i As Integer, b As String
b = " "
For i = 1 To n
b = b + Str$(st.ss(i)) + ","
Next
MsgBox b
End Sub
Sub succesor(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < n Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
Stiva este acea formă de organizare a datelor (structură de date) cu proprietatea că operaţiile de
introducere şi scoatere a datelor se fac în vârful ei.
Stivele se pot simula utilizând vectori.
Fie ST(i) un vector. ST(1), ST(2), ..., ST(n) pot reţine numai litere sau numai cifre. O variabilă K
indică în permanentă vârful stivei.
Exemplificăm, în continuare, modul de lucru cu stiva:
A În stiva iniţial vidă se introduce litera A, vârful stivei va fi la nivelul 1 (k-1);
B
A
introducem în stivă litera B, deci k va lua valoarea 2;
scoatem din stivă pe B (A nu poate fi scos);
A
scoatem din stivă pe A; stiva rămâne vidă
În mod practic la scoaterea unei variabile din stivă, scade cu 1 valoarea variabilei ce indică vârful
stivei, iar atunci când scriem ceva în stivă, o eventuală valoare reziduală se pierde:
Pe un anumit nivel se retine, de regulă, o singură informaţie (literă sau cifră), însă este posibil; aşa
cum va rezulta din exemplele, prezentate în lucrare, să avem mai multe informaţii, caz în care avem de a
face cu stive duble, triple, etc.
Întreaga teorie a recursivităţii se bazează pe structura de tip stivă.
75

74. Prezentarea tehnicii Backtracking
Această tehnică se foloseşte în rezolvarea problemelor care îndeplinesc simultan următoarele
condiţii:
– soluţia lor poate fi pusă sub forma unui vector S=x 1,x2, ...,xn, cu x1 € A1, x2 € A2 …, xn €
An
– mulţimile A1, A2 , …., An sunt mulţimi finite, iar elementele lor se consideră că se află
într-o relaţie de ordine bine stabilită;
– nu se dispune de o altă metodă de rezolvare, mai rapidă
– x1 x2 …, xn pot fi la rândul lor vectori;
– A1, A2 …, An pot coincide.
La întâlnirea unei astfel de probleme, dacă nu cunoaştem această tehnică, suntem tentaţi să
generăm toate elementele produsului cartezian A1,A2 …,An si fiecare element să fie testat dacă este
soluţie. Rezolvând problema în acest mod, timpul de execuţie este atât de mare, încât poate fi considerat
infinit, algoritmul neavând nici o valoare practică.
De exemplu, dacă dorim să generăm toate permutările unei mulţimi finite A, nu are rost să
generăm produsul cartezian AxAx.....xA, pentru ca apoi, să testăm, pentru fiecare element al acestuia,
dacă este sau nu permutare (nu are rost să generăm 1.1,1.......1, pentru ca apoi să constatăm că nu am
obţinut o permutare, când de la a doua cifră 1 ne puteam da seama că cifrele nu sunt distincte).
Tehnica Backtracking are la bază un principiu extrem de simplu:
– se construieşte soluţia pas cu pas: x1, x2 …,xn
– dacă se constată că, pentru o valoare aleasă, nu avem cum să ajungem la soluţie, se
renunţă la acea valoare şi se reia căutarea din punctul în care am rămas.
Concret:
– se alege primul element x, ce aparţine lui A;
– presupunând generate elementele x1,x2 …,xk , aparţinând mulţimilor A1, A2 …,Ak, se
alege (dacă există) xk+1, primul element disponibil din mulţimea Ak+1, apar două posibilităţi:
1) Nu s-a găsit un astfel de element, caz în care caz în care se reia căutarea considerând
generate elementele x1,x2 …,xk+1 , iar aceasta se reia de la următorul element al mulţimii
Ak rămas netestat;
2) A fost găsit, caz în care se testează dacă acesta îndeplineşte anumite condiţii de
continuare apărând astfel două posibilităţi:
 îndeplineşte, caz în care se testează dacă s-a ajuns la soluţie si apar din nou două
posibilităţi:
- s-a ajuns la soluţie, se tipăreşte soluţia si se reia algoritmul considerând generate
elementele x1,x2 …,xk, (se caută în continuare, un alt element al mulţimii A k, rămas
netestat);
- nu s-a ajuns la soluţie, caz în care se reia algoritmul considerând generate elementele
x1,x2 …,xk , si se caută un prim element xk+2 € Ak.
 nu le îndeplineşte caz în care se reia algoritmul considerând generate elementele x 1,x2
…, xk , iar elementul xk-1 se caută între elementele mulţimii A, rămase netestate.
Algoritmii se termină atunci când nu există nici un element x1 € A1 netestat.
Observaţie: tehnica Backtracking are ca rezultat obţinerea tuturor soluţiilor problemei. În cazul în care
se cere o sigură soluţie se poate forţa oprirea, atunci când a fost găsită.
Am arătat că orice soluţie se generează sub formă de vector. Vom considera că generarea soluţiilor
se face intr-o stivă. Astfel, x1 € A1, se va găsi pe primul nivel al stivei, x 2 € A2 se va găsi pe al doilea nivel
al stivei,... xk € Ak se va găsi pe nivelul k al stivei. În acest fel, stiva (notată ST) va arăta astfel:
76

75. ...
xk
…
…
x2
ST
x1
Nivelul k+1 al stivei trebuie iniţializat (pentru a alege, în ordine, elementele mulţimii
k+1 ). Iniţializarea trebuie făcută cu o valoare aflată (în relaţia de ordine considerată, pentru mulţimea
Ak+1 ) înaintea tuturor valorilor posibile din mulţime. De exemplu, pentru generarea permutărilor mulţimii
{1,2.....n}, orice nivel al stivei va lua valori de la 1 la n. Iniţializarea unui nivel (oarecare) se face cu
valoarea 0. Procedura de iniţializare o vom numi INIT şi va avea doi parametri: k (nivelul care trebuie
iniţializat si ST (stiva)).
Găsirea următorului element al mulţimii A k (element care a fost netestat) se face cu ajutorul
procedurii SUCCESOR (AS,ST,K). Parametrul AS (am succesor) este o variabilă booleană. În situaţia în
care am găsit elementul, acesta este pus în stivă şi AS ia valoarea TRUE, contrar (nu a rămas un element
netestat) AS ia valoarea FALSE..
Odată ales un element, trebuie văzut dacă acesta îndeplineşte condiţiile de continuare (altfel spus,
dacă elementul este valid). Acest test se face cu ajutorul procedurii VALID (EV,ST,K).
Testul dacă s-a ajuns sau nu la soluţia finală se face cu ajutorul funcţiei SOLUTIE(k) iar o soluţie
se tipăreşte cu ajutorul procedurii TIPAR. Prezentăm în continuare rutina Backtracking:
k:=1; CALL init(1,st);
while k>0
do
CALL succesor (as, st, k) ;
if as then CALLvalid(ev,st,k) then
loop until (not as) or (as and ev) ;
if as then
if solutie(k) then
CALL tipar
else
k:=k+l;
CALL init ( k, st );
end;
else
k:=k-1
wend
Observaţie: Problemele rezolvate prin această metodă necesită un timp îndelungat. Din acest motiv, este
bine să utilizăm metoda numai atunci când nu avem la dispoziţie un alt algoritm mai eficient. Cu toate că
există probleme pentru care nu se pot elabora alţi algoritmi mai eficienţi, tehnica backtracking trebuie
aplicată numai în ultimă instanţă.
Fiind dată o tablă de şah, de dimensiune n, x n, se cer toate soluţiile de aranjare a n dame, astfel
încât să nu se afle două dame pe aceeaşi linie, coloană sau diagonală (dame să nu se atace reciproc).
Exemplu: Presupunând că dispunem de o tablă de dimensiune 4x4, o soluţie ar fi următoarea:
77

76. D
D
D
D
Observăm că o damă trebuie să fie plasată singură pe linie. Plasăm prima damă pe linia 1, coloana 1.
D
A doua damă nu poate fi aşezată decât în coloana 3.
D
D
Observăm că a treia damă nu poate fi plasată în linia 3. Încercăm atunci plasarea celei de-a doua dame în
coloana 4.
D
D
A treia damă nu poate fi plasată decât în coloana 2.
78

77. D
D
D
În această situaţie dama a patra nu mai poate fi aşezată.
Încercând să avansăm cu dama a treia, observăm că nu este posibil să o plasăm nici în coloana 3,
nici în coloana 4, deci o vom scoate de pe tablă. Dama a doua nu mai poate avansa, deci şi ea este scoasă
de pe tablă. Avansăm cu prima damă în coloana 2.
D
A doua damă nu poate fi aşezată decât în coloana 4.
D
D
Dama a treia se aşează în prima coloană.
D
D
D
79

78. Acum este posibil să plasăm a patra damă în coloana 3 si astfel am obţinut o soluţie a problemei.
D
D
D
D
Algoritmul continuă în acest mod până când trebuie scoasă de pe tablă prima damă.
Pentru reprezentarea unei soluţii putem folosi un vector cu n componente (având în vedere că pe
fiecare linie se găseşte o singură damă).
Exemplu pentru soluţia găsită avem vectorul ST ce poate fi asimilat unei stive.
Două dame se găsesc pe aceeaşi diagonală dacă si numai dacă este îndeplinită condiţia: |st(i)-st(j)|
=|i-j| ( diferenţa, în modul, între linii si coloane este aceeaşi).
În general ST(i)=k semnifică faptul că pe linia i dama ocupă poziţia k.
3 ST(4)
1 ST(3)
4 ST(2)
2 ST(1)
Exemplu: în tabla 4 x4 avem situaţia:
D
st(1)= 1 i = 1
D st(3)= 3 j = 3
D |st(1) - st(3)| = |1 – 3| = 2
D |i – j| = |1 – 3| = 2
sau situaţia
D
D
D
D
st(1) = 3 i = 1
st(3) = 1 j = 3
|st(i) - st(j)| = |3 – 1| = 2
|i – j| = |1 – 3| = 2
80

79. Întrucât doua dame nu se pot găsi în aceeaşi coloană, rezultă că o soluţie este sub formă de
permutare. O primă idee ne conduce la generarea tuturor permutărilor si la extragerea soluţiilor pentru
problema ca două dame să nu fie plasate în aceeaşi diagonală. A proceda astfel, înseamnă că lucrăm
conform strategiei backtracking. Aceasta presupune ca imediat ce am găsit două dame care se atacă, să
reluăm căutarea.
Iată algoritmul, conform strategiei generate de backtracking:
– În prima poziţie a stivei se încarcă valoarea 1, cu semnificaţia că în linia unu se aşează
prima damă în coloană.
– Linia 2 se încearcă aşezarea damei în coloana 1, acest lucru nefiind posibil întrucât
avem doua dame pe aceeaşi coloană.
– În linia 2 se încearcă aşezarea damei în coloana 2 , însă acest lucru nu este posibil,
pentru că damele se găsesc pe aceiaşi diagonală (|st(1)-st(2)|=|1-2|);
– Aşezarea damei 2 în coloana 3 este posibilă.
– Nu se poate plasa dama 3 în coloana 1, întrucât în liniile 1-3 damele ocupa acelaşi
coloană.
– Şi această încercare eşuează întrucât damele de pe 2 şi 3 sunt pe aceeaşi diagonală.
– Damele de pe 2-3 se găsesc pe aceeaşi coloană.
– Damele de pe 2-3 se găsesc pe aceeaşi diagonală.
– Am coborât în stivă mutând dama de pe linia 2 şi coloana 3 în coloana 4.
Algoritmul se încheie atunci când stiva este vidă. Semnificaţia procedurilor utilizate este
următoarea:
INIT - nivelul k al stivei este iniţializat cu 0;
SUCCESOR - măreşte cu 1 valoarea aflată pe nivelul k al stivei în situaţia în care aceasta
este mai mică decât n şi atribuie variabilei EV valoarea TRUE, în caz contrar, atribuie
variabilei EV valoarea FALSE;
VALID - validează valoarea pusă pe nivelul k al stivei, verificând dacă nu avem două
dame pe aceeaşi linie (st(k)=st(i)), sau dacă nu avem două dame pe aceeaşi diagonală
(st(k)-st(i)=|k-i|)caz în care variabilei EV i se atribuie FALSE; în caz contrar, variabilei EV
i se atribuie TRUE;
SOLUTIE - verifică dacă stiva a fost completată până la nivelul n inclusiv;
TIPAR - tipăreşte o soluţie.
Subprogramele prezentate in limbajul Visual Basic sunt descrise mai jos:
Global n As Integer, am_suc As Boolean, ev As Boolean
Type stiva
ss(100) As Integer
End Type
Global st As stiva
Sub init(k As Integer, st As stiva)
st.ss(k) = 0
End Sub
Sub succesor(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < n Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
81

80. Sub valid(ev As Boolean, st As stiva, k As Integer)
ev = True
For i = 1 To k - 1
If (st.ss(i) = st.ss(k)) Or (Abs(st.ss(i) - st.ss(k)) = Abs(k -
i)) Then
ev = False
End If
Next
End Sub
Function solutie(k As Integer) As Integer
If k = n Then
solutie = True
Else
solutie = False
End If
End Function
Sub tipar()
Dim i As Integer, b As String
b = " "
For i = 1 To n
b = b + "(" + Str$(i) + "," + Str$(st.ss(i)) + "),"
Next
MsgBox b
End Sub
Sub back()
Dim k As Integer
k = 1
While k > 0
Do
succesor am_suc, st, k
If am_suc = True Then
valid ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tipar
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
End Sub
Sub Button2_Click()
n = InputBox("n=", ib_title)
back
End Sub
Produsul cartezian a n mulţimi. Se dau mulţimile de mai jos şi se cere produsul cartezian al lor.
A1 = {1, 2, 3, …, k1}
82

81. A2 = {1, 2, 3, …, k2}
………………………
An = {1, 2, 3, …, kn}
Exemplu: A1 = {1, 2}
A2 = {1, 2, 3}
A3 = {1, 2, 3}
A1 × A2 × A3 = {(1, 1, 1), (1, 1, 2), (1, 1, 3), (1, 2, 1), (1, 2, 2), (1, 2, 3), (1, 3, 1), (1, 3, 2), (1, 3, 3),
(2, 1, 1), (2, 1, 2), (2, 1, 3), (2, 2, 1), (2, 2, 2), (2, 2, 3), (2, 3, 1), (2, 3, 2), (2, 3, 3)}.
Pentru rezolvare, se folosesc stiva ST şi un vector A ce reţine numerele k 1, k2, …kn. Utilizăm
metoda backtracking, uşor modificată din următoarele motive:
a) Orice element aflat la nivelul k al stivei este valid, motiv pentru care procedura valid nu
face altceva decât să atribuie variabilei ev valoarea TRUE.
b) Limita superioară pe nivelul k al stivei este dată de A(k).
Modul de concepere a algoritmului rezultă din cele ce urmează:
1 2 3 1
1 1 1 2 2
1 1 1 1 1 1
2 3 1 2 3
2 2 3 3 3 3
1 1 1 1 1 1
Observaţii:
Algoritmul prezentat aici este de tip backtracking? Întrebarea are sens pentru că este absent mecanismul
de întoarcere. Vom admite că şi aceasta este backtracking, dar „degenerat”.
Private Sub CommandButton16_Click()
Dim a As vector
cit_n "n=", n
cit_date "a", n, a
tipar " multimile sunt : ", n, a
back_prod_cart
End Sub
Sub cit_n(mes As String, nnn As Integer)
Do
nnn = InputBox(mes, y)
Loop Until n > 0 And n < 100
End Sub
Sub cit_date(mes As String, n As Integer, a As vector)
For i = 1 To n
a.v(i) = InputBox(mes + "(" + Str$(i) + ")=", y)
Next
End Sub
83

82. Sub tipar(mes As String, n As Integer, a As vector)
sir = ""
For i = 1 To n
sir = sir + Str$(a.v(i)) + ","
Next
MsgBox mes + " " + sir
End Sub
Sub back_prod_cart()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor_prod am_suc, st, k
If am_suc = True Then
valid_prod ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tipar_r
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
End Sub
Sub valid_prod(ev As Boolean, st As stiva, k As Integer)
ev = True
End Sub
Function solutie(k As Integer) As Boolean
If k = n Then
solutie = True
Else
solutie = False
End If
End Function
Sub succesor_prod(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < a.v(k) Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
Sub init(k As Integer, st As stiva)
st.ss(k) = 0
End Sub
Generarea aranjamentelor. Se citesc n şi p. Să se genereze toate aranjamentele de n luate câte p.
84

83. Din analiza problemei rezultă următoarele:
– stiva are înălţimea p;
– fiecare nivel ia valori între 1 şi n;
– elementele plasate pe diverse niveluri trebuie să fie distincte.
Algoritmul este asemănător cu cel de la permutări, cu deosebirea că aici stipa are înălţimea p.
Private Sub CommandButton17_Click()
cit_n "n = ", n
cit_n "p = ", p
back_aranj
End Sub
Sub back_aranj()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor am_suc, st, k
If am_suc = True Then
valid1 ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie1(k) Then
tipar_rr
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
End Sub
Sub valid1(ev As Boolean, st As stiva, k As Integer)
ev = True
For i = 1 To k - 1
If (st.ss(i) = st.ss(k)) Then
ev = False
End If
Next
End Sub
Sub tipar_rr()
Dim i As Integer, b As String
b = " "
For i = 1 To p
b = b + Str$(st.ss(i)) + ","
Next
MsgBox b
End Sub
Function solutie1(k As Integer) As Boolean
If k = p Then
85

84. solutie1 = True
Else
solutie1 = False
End If
End Function
Sub succesor(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < n Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
Sub init(k As Integer, st As stiva)
st.ss(k) = 0
End Sub
Generarea combinărilor. Se citesc n şi p numere naturale, n≥p. Se cere să se genereze toate
submulţimile cu p elemente ale mulţimii {1, 2, 3, …, n}.
Pentru rezolvarea problemei trebuie ţinut cont de următoarele:
– stiva are înălţimea p;
– elementele aflate pe niveluri diferite ale stivei trebuie să fie distincte;
– pentru a evita repetiţia elementele se aşează în ordine crescătoare: pe nivelul k se va afla
o valoare mai mare decât pe nivelul k-1 şi mai mică sau egală cu n-p+k.
Private Sub CommandButton18_Click()
cit_n "n = ", n
cit_n "p = ", p
back_comb
End Sub
Sub back_comb()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor_c am_suc, st, k
If am_suc = True Then
valid_c ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie1(k) Then
tipar_rr
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
End Sub
86

85. Sub succesor_c(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < n - p + k Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
Sub valid_c(ev As Boolean, st As stiva, k As Integer)
Dim i As Integer
ev = True
For i = 1 To k - 1
If (st.ss(i) = st.ss(k)) Then
ev = False
End If
Next
If k > 1 Then
If st.ss(k) < st.ss(k - 1) Then
ev = False
End If
End If
End Sub
Function solutie1(k As Integer) As Boolean
If k = p Then
solutie1 = True
Else
solutie1 = False
End If
End Function
Sub tipar_col()
Dim i As Integer, b As String
b = " "
For i = 1 To n
b = b + "Tara = " + Str$(i) + "; culoarea " + Str$(st.ss(i)) + " "
Next
MsgBox b
End Sub
Problema comis-voiajorului. Un comis voiajor trebuie să viziteze un număr n de oraşe. Iniţial, el
se află într-unul dintre ele, notat 1. Comis – voiajorul doreşte să nu treacă de două ori prin acelaşi oraş, iar
la întoarcere să revină în oraşul 1. Cunoscând legăturile existente între oraşe, se cere să se tipărească toate
drumurile posibile pe care le poate efectua comis – voiajorul.
Exemplu: În figura alăturată sunt simbolizate cele 6 oraşe, precum şi drumurile existente între ele.
2 3
87

86. 1 4
6 5
Comis - voiajorul are următoarele posibilităţi de parcurgere:
1, 2, 3, 4, 5, 6, 1;
1, 2, 5, 4, 3, 6, 1;
1, 6, 3, 4, 5, 2, 1;
1, 6, 5, 4, 3, 2, 1;
Legăturile existente între oraşe sunt date în matricea An,n. Elementele matricei A pot fi 0 sau 1
(matricea este binară).
1, dacă există drum între oraşele i şi j;
A(i,j) =
0 , altfel
Se observă că A(i,j) = A(j,i), oricare ar fi i,j ∈{1, 2, 3, …, n} – matricea este simetrică.
Pentru rezolvarea problemei folosim stiva st. la baza stivei (nivelul 1) se încarcă numărul 1.
Prezentăm în continuare modul de rezolvare a problemei.
2
De la oraşul 1 la oraşul 2 există drum, deci se va urca în stivă;
1
2
2 Oraşul 2 se mai găseşte în stivă, deci nu este acceptat;
1
3
De la oraşul 2 la oraşul 3 se găseşte drum; prin oraşul 3 nu s-a mai trecut, deci
2
oraşul 3 este acceptat.
1
Algoritmul continuă în acest mod până se ajunge din nou la nivelul 1, caz în care algoritmul se
încheie.
Un succesor, între 2 şi n, aflat pe nivelul k al stivei, este considerat valid dacă sunt îndeplinite
următoarele condiţii:
– nu s-a mai trecut prin oraşul simbolizat de succesor, deci acesta nu se regăseşte în stivă;
– există drum între oraşul aflat la nivelul k-1 şi cel aflat la nivelul k;
– dacă succesorul se găseşte la nivelul n, să existe drum de la el la oraşul 1.
Observaţii:
1. Problemele rezolvate prin această metodă necesită un timp îndelungat de execuţie. Din
acest motiv este bine să utilizăm metoda atunci numai atunci când nu mai avem la
dispoziţie un alt algoritm mai eficient
2. Menţionăm că nu există probleme pentru care nu se cunosc algoritmi eficienţi de
rezolvare, deci backtracking este indicată.
88

87. 3. Rezolvarea iterativă încalcă principiul stivei atunci când verificăm condiţiile de
continuare, sau atunci când tipărim soluţia găsită, pentru că accesăm orice nivel al stivei.
Consider că o structură trebuie folosită ca atare atunci când este strict necesar. De exemplu,
chiar şi segmentul de stivă al calculatorului poate fi accesat oriunde. Asta nu înseamnă că
acolo nu se utilizează din plin „mecanismul” stivei.
Sub back_comis()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor_col am_suc, st, k
If am_suc = True Then
valid_col ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tipar_col
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
End Sub
Sub succesor_comis(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < n Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
Sub valid_comis(ev As Boolean, st As stiva, k As Integer)
ev = True
For i = 1 To k - 1
If (st.ss(i) = st.ss(k)) And (mat.m(i, k) = 1) Then
ev = False
End If
Next
End Sub
Sub tipar_comis()
Dim i As Integer, b As String
b = " "
For i = 1 To n
b = b + "Tara = " + Str$(i) + "; vizitat " + Str$(st.ss(i)) + " "
Next
MsgBox b
End Sub
89

88. PROBLEMA COLORĂRII HĂRŢILOR
Enunţ:
Fiind dată o hartă cu n ţări, se cer toate soluţiile de colorare a hărţii, utilizând cel mult patru culori,
astfel încât două ţări de frontieră comună să fie colorate diferit. Este demonstrat faptul că sunt suficiente
numai patru culori pentru ca orice hartă să poată fi colorată.
Rezolvare:
Pentru exemplificare, vom considera următoarea hartă unde ţările sunt numerotate cu cifre
cuprinse între 1 şi 5:
1
4
3
2
5
Figura 9.1 Harta ţărilor
O soluţie a acestei probleme este următoarea:
ţara 1 – culoarea 1
ţara 2 – culoarea 2
ţara 3 – culoarea 1
ţara 4 – culoarea 3
ţara 5 – culoarea 4
Harta este furnizată programului cu ajutorul unei matrice An,n
1, dacă ţara i se învecinează cu ţara j;
A(i,j) =
0 , altfel
Matricea A este simetrică. Pentru rezolvarea problemei se utilizează stiva st, unde nivelul k al
stivei simbolizează ţara k, iar st[k] culoarea ataşată ţării k. Stiva are înălţimea n şi pe fiecare nivel ia
valori între 1 şi 4.
Sub back_col()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor_col am_suc, st, k
If am_suc = True Then
valid_col ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tipar_col
Else
k = k + 1
init k, st
End If
90

89. Else
k = k - 1
End If
Wend
End Sub
Sub succesor_col(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < 4 Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
Sub valid_col(ev As Boolean, st As stiva, k As Integer)
ev = True
For i = 1 To k - 1
If (st.ss(i) = st.ss(k)) And (mat.m(i, k) = 1) Then
ev = False
End If
Next
End Sub
Sub tipar_col()
Dim i As Integer, b As String
b = " "
For i = 1 To n
b = b + "Tara = " + Str$(i) + "; culoarea " + Str$(st.ss(i)) + " "
Next
MsgBox b
End Sub
Sub tipar_rr()
Dim i As Integer, b As String
b = " "
For i = 1 To p
b = b + Str$(st.ss(i)) + ","
Next
MsgBox b
End Sub
91

90. CAPITOLUL X
METODA DIVIDE ET IMPERA
Metoda de programare DIVIDE ET IMPERA consta in impartirea problemei initiale de
dimensiuni [n] in doua sau mai multe probleme de dimensiuni reduse. In general se executa impartirea in
doua subprobleme de dimensiuni aproximativ egale si anume [n/2]. Impartirea in subprobleme are loc
pana cand dimensiunea acestora devine suficient de mica pentru a fi rezolvate in mod direct(cazul de
baza). Dupa rezolvarea celor doua subprobleme se executa faza de combinare a rezultatelor in vederea
rezolvarii intregii probleme.
Metoda DIVIDE ET IMPERA se poate aplica in rezolvarea unei probleme care indeplineste
urmatoarele conditii:
 se poate descompune in (doua sau mai multe) suprobleme;
 aceste suprobleme sunt independente una fata de alta (o subproblema nu se rezolva pe
baza alteia si nu se foloseste rezultate celeilalte);
 aceste subprobleme sunt similare cu problema initiala;
 la randul lor subproblemele se pot descompune (daca este necesar) in alte subprobleme
mai simple;
 aceste subprobleme simple se pot solutiona imediat prin algoritmul simplificat.
Deoarece putine probleme indeplinesc conditiile de mai sus ,aplicarea metodei este destul de rara.
Dupa cum sugereaza si numele "desparte si stapaneste "etapele rezolvarii unei probleme (numita
problema initiala) in DIVIDE ET IMPERA sunt :
 descompunerea problemei initiale in subprobleme independente, smilare problemei de
baza, de dimensiuni mai mici;
 descompunerea treptata a subproblemelor in alte subprobleme din ce in ce mai simple,
pana cand se pot rezolva imediata ,prin algoritmul simplificat;
 rezolvarea subproblemelor simple;
 combinarea solutiilor gasite pentru construirea solutiilor subproblemelor de dimensiuni
din ce in ce mai mari;
 combinarea ultimelor solutii determina obtinerea solutiei problemei initiale
Metoda DIVIDE ET IMPERA admite o implementare recursiva, deorece subproblemele sunt
similare problemei initiale, dar de dimensiuni mai mici.
Principiul fundamental al recursivitatii este autoapelarea unui subprogram cand acesta este activ;
ceea ce se intampla la un nivel, se intampla la orice nivel, avand grija sa asiguram conditia de terminare
ale apelurilor repetate. Asemanator se intampla si in cazul metodei DIVITE ET IMPERA; la un anumit
nivel sunt doua posibilitati:
 s-a ajuns la o (sub)problema simpla ce admite o rezolvare imediata caz in care se
rezolva (sub)problema si se revine din apel (la subproblema anterioara, de dimensiuni mai
mari);
 s-a ajuns la o (sub)problema care nu admite o rezolvare imediata, caz in care o
descompunem in doua sau mai multe subprobleme si pentru fiecare din ele se continua
apelurile recursive (ale procedurii sau functiei).
In etapa finala a metodei DIVIDE ET IMPERA se produce combinarea subproblemelor
(rezolvate deja) prin secventele de revenire din apelurile recursive.
Etapele metodei DIVIDE ET IMPERA (prezentate anterior) se pot reprezenta prin urmatorul
subprogram general (procedura sau functie )recursiv exprimat in limbaj natural:
Subprogram DIVIMP (PROB);
Daca PROBLEMA PROB este simpla
Atunci se rezolva si se obtine solutia SOL
Altfel pentru i=1,k executa DIVIMP(PROB) si se obtine SOL1;
92

91. Se combina solutiile SOL 1,... ,SOL K si se obtine SOL;
Sfarsit_subprogram;
Deci, subprogramul DIVIMP se apeleaza pentru problema initiala PROB; aceasta admite
descompunerea in K subprobleme simple; pentru acestea se reapeleaza recursiv subprogramul; in final se
combina solutiile acestor K subprobleme.
De obicei problema initiala se descompune in doua subprobleme mai simple; in acest caz etapele
generale ale metodei DIVIDE ET IMPERA se pot reprezenta concret, in limbaj pseudocod, printr-o
procedura recursiva astfel:
Procedura DIVIMP(li,ls,sol);
Daca ((ls-li)<=eps)
Atunci REZOLVA (li,ls,sol);
Altfel
DIVIDE (li,m,ls);
DIVIMP(li,msol1);
DIVIMP(m,ls,sol2);
COMBINA(sol1,sol2,sol);
Sfarsit_procedura;
Procedura DIVIMP se apeleaza pentru problema initiala care are dimensiunea intre limita
inferioara (li) si limita inferioara(ls); daca (sub)problema este simpla (ls-li<=eps), atunci procedura
REZOLVA ii afla solutia imediat si se produce intoarcerea din apelul recursiv; daca (sub)problema este
(inca) complexa, atunci procedura DIVIDE o imparte in doua subprobleme, alegand pozitia m intre
limitele li si ls; pentru fiecare din cele doua subprobleme se reapeleaza recursiv procedura DIVIMP; in
final, la intoarcerile din apeluri se produce combinarea celor doua soluitii sol1 si sol2 prin apelul
procedurii COMBINA.
PROBLEMA TURNURILOR DIN HANOI
Prezentarea algoritmului rezolvarii
Fie trei tije verticale notate A,B,C. Pe tija A se gasesc asezate n discuri de diametre diferite, in
ordinea crescatoare a diametrelor, privind de sus in jos. Initial, tijele B si C sunt goale. Sa se afiseze toate
mutarile prin care discurile de pe tija A se muta pe tija B, in aceeasi ordine, folosind ca tija de manevra C
si resspectand urmatoarele reguli:
– la fiecare pas se muta un singur disc;
– un disc se poate aseza numai peste un disc cu diametrul mai mare.
Rezolvarea acestei probleme se bazeaza pe urmatoarele considerente logice:
– daca n=1, atunci mutarea este immediata AàB (mut discul de pe A pe B);
– daca n=2, atunci sirul mutarilor este: AàC,AàB,CàB;
– daca n>2 procedam astfel :
- mut (n-1) discuri AàC;
- mut un disc AàB;
- mut cele (n-1) discuri CàB.
Observam ca problema initiala se descompune in trei subprobleme mai simple, similare problemei
initiale: mut (n-1)discuri AàC, mut ultimul disc pe B, mut cele (n-1)discuri C-->B. Dimensiunile acestor
subprobleme sunt: n-1,1,n-1.
Aceste subprobleme sunt independente, deoarece tijele initial (pe care sunt dispuse discurile),
tijele finale si tijele intermediare sunt diferite. Notam H(n,A,B,C)=sirul mutarilor a n discuri de pe A pe
B, folosind C.
PENTRU
n=1 AàB
n>1 H(n,A,B,C)= H(n-1,A,C,B),AB, H(n-1,C,B,A)
93

92. Sortare rapida (quicksort)
Un tablou V se completeaza cu n elemente numere reale .Sa se ordoneze crescator folosind
metoda de sortare rapida .
Solutia problemei se bazeaza pe urmatoarele etape implementate in programul principal:
 se apeleaza procedura “quick” cu limita inferioara li=1 si limita superioara ls=n;
 functia”poz” realizeaza mutarea elementului v[i] exact pe pozitia ce o va ocupa acesta
in vectorul final ordonat ; functia”poz” intoarce (in k ) pozitia ocupata de acest element;
 in acest fel , vectorul V se imparte in doua parti: li …k-1 si k+1…ls;
 pentru fiecare din aceste parti se reapeleaza procedura ”quick”, cu limitele modificate
corespunzator;
 in acest fel, primul element din fiecare parte va fi pozitionat exact pe pozitia finala ce o
va ocupa in vectorul final ordonat (functia”poz”);
 fiecare din cele doua parti va fi, astfel, inpartita in alte doua parti; procesul continua
pana cand limitele partilor ajung sa se suprapuna ,ceea ce indica ca toate elementele
vectorului au fost mutate exact pe pozitiile ce le vor ocupa in vectorul final ;deci vectorul
este ordonat ;
 in acest moment se produc intoarcerile din apelurile recursive si programul isi termina
executia.
Observaţii:
– daca elementul se afla in stanga, atunci se compara cu elementele din dreapta lui si se
sar (j:=j-1) elementele mai mari decat el;
– daca elementul se afla in dreapta, atunci se compara cu elemente din stanga lui si se sar
(i:=i+1) elementele mai mici decat el.
Sortare prin interclasare(mergesort)
Tabloul unidimensional V se completeaza cu n numere reale. Sa se ordoneze crescator folosind
sortare prin interclasare.
Sortarea prin interclasare se bazeaza pe urmatoarea logica:
– vectorul V se imparte, prin injumatatiri succesive,in vectori din ce in ce mai mici;
– cand se ating vectorii de maxim doua elemente, fiecare dintre acestia se ordoneaza
printr-o simpla comparare a elementelor;
– cate doi astfel de mini-vectori ordonati se interclaseaza succesiv pana se ajunge iar la
vectorul V.
Observaţii:
– mecanismul general de tip Divide et Impera se gaseste implementat in procedura “divi”;
– astfel de abordare a problemei sortarii unii vector conduce la economie de timp de
calcul, deoarece operatia de interclasare a doi vectori deja ordonati este foarte rapida, iar
ordonarea independenta celor doua jumatati (mini-vectori) consuma in total aproximativ a
doua parte din timpul care ar fi necesar ordonarii vectorului luat ca intreg .
CONCLUZII LA TEHNICA DIVIDE ET IMPERA
Sortare prin insertie binara
Sa se ordoneze crescator un tablou unidimensional V de n numere reale, folosind sortarea prin
insertie binara.
Pentru fiecare element v[i] se procedeaza in patru pasi:
1. se considera ordonate elementele v[1],v[2],….,v[i-1];
2. se cauta pozitia k pe care urmeaza s-o ocupe v[i] intre elementele v[1],v[2],…,v[i-1]
(procedura “poz” prin cautare binara);
3. se deplaseaza spre dreapta elementele din pozitiile k,k+1,…,n (procedura “deplasare”);
94

93. 4. insereaza elementul v[i] in pozitia k (procedura”deplasare”);
Se obtine o succesiune de k+1 elemente ordonate crescator.
Analiza a complexitatii timp pentru algoritmii Divide et Impera
Algoritmii de tip Divide et Impera au buna comportare in timp, daca se indeplinesc urmatoarele
conditii:
– dimensiunile subprogramelor (in care se imparte problema initiala) sunt aproximativ
egale (“principiul balansarii”);
– lipsesc fazele de combinare a solutiilor subproblemelor (cautare binara).
95

94. CAPITOLUL XI
METODA GREEDY
11.1 Algoritmi greedy
Pusi in fata unei probleme pentru care trebuie sa elaboram un algoritm, de multe ori “nu stim cum
sa incepem”. Ca si in orice alta activitate, exista cateva principii generale care ne pot ajuta in aceasta
situatie. Ne propunem sa prezentam in urmatoarele capitole tehnicile fundamentale de elaborare a
algoritmilor. Cateva din aceste metode sunt atat de generale, incat le folosim frecvent, chiar daca numai
intuitiv, ca reguli elementare in gandire.
11.2 Tehnica greedy
Algoritmii greedy (greedy = lacom) sunt in general simpli si sunt folositi la probleme de
optimizare, cum ar fi: sa se gaseasca cea mai buna ordine de executare a unor lucrari pe calculator, sa se
gaseasca cel mai scurt drum intr-un graf etc. In cele mai multe situatii de acest fel avem:
 multime de candidati (lucrari de executat, varfuri ale grafului etc)
 o functie care verifica daca o anumita multime de candidati constituie o solutie posibila
 o functie care verifica daca o multime de candidati este fezabila, adica daca este posibil
sa completam aceasta multime astfel incat sa obtinem o solutie posibila, nu neaparat
optima, a problemei
 o functie de selectie care indica la orice moment care este cel mai promitator dintre
candidatii inca nefolositi
 o functie obiectiv care da valoarea unei solutii (timpul necesar executarii tuturor
lucrarilor intr-o anumita ordine, lungimea drumului pe care l-am gasit etc); aceasta este
functia pe care urmarim sa o optimizam (minimizam/maximizam)
Pentru a rezolva problema noastra de optimizare, cautam o solutie posibila care sa optimizeze
valoarea functiei obiectiv. Un algoritm greedy construieste solutia pas cu pas. Initial, multimea
candidatilor selectati este vida. La fiecare pas, incercam sa adaugam acestei multimi cel mai promitator
candidat, conform functiei de selectie. Daca, dupa o astfel de adaugare, multimea de candidati selectati nu
mai este fezabila, eliminam ultimul candidat adaugat; acesta nu va mai fi niciodata considerat. Daca, dupa
adaugare, multimea de candidati selectati este fezabila, ultimul candidat adaugat va ramane de acum
incolo in ea. De fiecare data cand largim multimea candidatilor selectati, verificam daca aceasta multime
nu constituie o solutie posibila a problemei noastre. Daca algoritmul greedy functioneaza corect, prima
solutie gasita va fi totodata o solutie optima a problemei. Solutia optima nu este in mod necesar unica: se
poate ca functia obiectiv sa aiba aceeasi valoare optima pentru mai multe solutii posibile. Descrierea
formala a unui algoritm greedy general este:
function greedy(C)
{C este multimea candidatilor}
S← ø {S este multimea in care construim solutia}
while not solutie(S) and C ≠ ø do
x ← un element din C care maximizeaza/minimizeaza select(x)
C ← C {x}
if fezabil(S ∪ {x}) then S ← S ∪ {x}
if solutie(S) then return S
else return “nu există soluţie”
96

95. Este de inteles acum de ce un astfel de algoritm se numeste “lacom” (am putea sa-i spunem si
“nechibzuit”). La fiecare pas, procedura alege cel mai bun candidat la momentul respectiv, fara sa-i pese
de viitor si fara sa se razgandeasca. Daca un candidat este inclus in solutie, el ramane acolo; daca un
candidat este exclus din solutie, el nu va mai fi niciodata reconsiderat. Asemenea unui intreprinzator
rudimentar care urmareste castigul imediat in dauna celui de perspectiva, un algoritm greedy actioneaza
simplist. Totusi, ca si in afaceri, o astfel de metoda poate da rezultate foarte bune tocmai datorita
simplitatii ei.
Functia select este de obicei derivata din functia obiectiv; uneori aceste doua functii sunt chiar
identice.
Un exemplu simplu de algoritm greedy este algoritmul folosit pentru rezolvarea urmatoarei
probleme. Sa presupunem ca dorim sa dam restul unui client, folosind un numar cat mai mic de monezi.
In acest caz, elementele problemei sunt:
 candidatii: multimea initiala de monezi de 1, 5, si 25 unitati, in care presupunem ca din
fiecare tip de moneda avem o cantitate nelimitata
 solutie posibila: valoarea totala a unei astfel de multimi de monezi selectate trebuie sa
fie exact valoarea pe care trebuie sa o dam ca rest
 multime fezabila: valoarea totala a unei astfel de multimi de monezi selectate nu este
mai mare decat valoarea pe care trebuie sa o dam ca rest
 functia de selectie: se alege cea mai mare moneda din multimea de candidati ramasa
 functia obiectiv: numarul de monezi folosite in solutie; se doreste minimizarea acestui
numar
Se poate demonstra ca algoritmul greedy va gasi in acest caz mereu solutia optima (restul cu un
numar minim de monezi). Pe de alta parte, presupunand ca exista si monezi de 12 unitati sau ca unele din
tipurile de monezi lipsesc din multimea initiala de candidati, se pot gasi contraexemple pentru care
algoritmul nu gaseste solutia optima, sau nu gaseste nici o solutie cu toate ca exista solutie.
Evident, solutia optima se poate gasi incercand toate combinarile posibile de monezi. Acest mod
de lucru necesita insa foarte mult timp.
Un algoritm greedy nu duce deci intotdeauna la solutia optima, sau la o solutie. Este doar un
principiu general, urmand ca pentru fiecare caz in parte sa determinam daca obtinem sau nu solutia
optima.
11.3 Minimizarea timpului mediu de asteptare
O singura statie de servire (procesor, pompa de benzina etc) trebuie sa satisfaca cererile a n clienti.
Timpul de servire necesar fiecarui client este cunoscut in prealabil: pentru clientul i este necesar un timp
ti, 1 ≤ i ≤ n. Dorim sa minimizam timpul total de asteptare
(timpul de asteptare pentru clientul i)
ceea ce este acelasi lucru cu a minimiza timpul mediu de asteptare, care este T/n. De exemplu, daca avem
trei clienti cu t1 = 5, t2 = 10, t3 = 3, sunt posibile sase ordini de servire. In primul caz, clientul 1 este servit
primul, clientul 2 asteapta pana este servit clientul 1 si apoi este servit, clientul 3 asteapta pana sunt serviti
clientii 1, 2 si apoi este servit. Timpul total de asteptare a celor trei clienti este 38.
Ordinea T
1 2 3 5+(5+10)+(5+10+3) = 38
1 3 2 5+(5+3)+(5+3+10) = 31
2 1 3 10+(10+5)+(10+5+3) = 43
2 3 1 10+(10+3)+(10+3+5) = 41
3 1 2 3+(3+5)+(3+5+10) = 29 ←
optim
97

96. 3 2 1 3+(3+10)+(3+10+5) = 34
Algoritmul greedy este foarte simplu: la fiecare pas se selecteaza clientul cu timpul minim de
servire din multimea de clienti ramasa. Vom demonstra ca acest algoritm este optim.
Fie I = (i1 i2 ... in) o permutare oarecare a intregilor {1, 2, ..., n}. Daca servirea are loc in ordinea I,
avem
Presupunem acum ca I este astfel incat putem gasi doi intregi a < b cu
Interschimbam pe ia cu ib in I; cu alte cuvinte, clientul care a fost servit al b-lea va fi servit acum al
a-lea si invers. Obtinem o noua ordine de servire J, care este de preferat deoarece
Prin metoda greedy obtinem deci intotdeauna planificarea optima a clientilor.
Problema poate fi generalizata pentru un sistem cu mai multe statii de servire.
Interclasarea optima a sirurilor ordonate
Sa presupunem ca avem doua siruri S1 si S2 ordonate crescator si ca dorim sa obtinem prin
interclasarea lor sirul ordonat crescator care contine elementele din cele doua siruri. Daca interclasarea
are loc prin deplasarea elementelor din cele doua siruri in noul sir rezultat, atunci numarul deplasarilor
este #S1 + #S2.
Generalizand, sa consideram acum n siruri S1, S2, ..., Sn, fiecare sir Si, 1 ≤ i ≤ n, fiind format din qi
elemente ordonate crescator (vom numi qi lungimea lui Si). Ne propunem sa obtinem sirul S ordonat
crescator, continand exact elementele din cele n siruri. Vom realiza acest lucru prin interclasari succesive
de cate doua siruri. Problema consta in determinarea ordinii optime in care trebuie efectuate aceste
interclasari, astfel incat numarul total al deplasarilor sa fie cat mai mic. Exemplul de mai jos ne arata ca
problema astfel formulata nu este banala, adica nu este indiferent in ce ordine se fac interclasarile.
Fie sirurile S1, S2, S3 de lungimi q1 = 30, q2 = 20, q3 = 10. Daca interclasam pe S1 cu S2, iar
rezultatul il interclasam cu S3, numarul total al deplasarilor este (30+20)+(50+10)=110. Daca il
interclasam pe S3 cu S2, iar rezultatul il interclasam cu S1, numarul total al deplasarilor este
(10+20)+(30+30)=90.
Atasam fiecarei strategii de interclasare cate un arbore binar in care valoarea fiecarui varf este data
de lungimea sirului pe care il reprezinta. Daca sirurile S1, S2, ..., S6 au lungimile q1 = 30, q2 = 10, q3 = 20,
q4 = 30, q5 = 50, q6 = 10, doua astfel de strategii de interclasare sunt reprezentate prin arborii din Figura
11.1.
Figura 11.1 Reprezentarea strategiilor de interclasare.
98

97. Observam ca fiecare arbore are 6 varfuri terminale, corespunzand celor 6 siruri initiale si 5 varfuri
neterminale, corespunzand celor 5 interclasari care definesc strategia respectiva. Numerotam varfurile in
felul urmator: varful terminal i, 1 ≤ i ≤ 6, va corespunde sirului Si, iar varfurile neterminale se
numeroteaza de la 7 la 11 in ordinea obtinerii interclasarilor respective (Figura 11.2).
Figura 11.2 Numerotarea varfurilor arborilor din Figura 11.1
Strategia greedy apare in Figura 11.1b si consta in a interclasa mereu cele mai scurte doua siruri
disponibile la momentul respectiv.
Interclasand sirurile S1, S2, ..., Sn, de lungimi q1, q2, ..., qn, obtinem pentru fiecare strategie cate un
arbore binar cu n varfuri terminale, numerotate de la 1 la n, si n–1 varfuri neterminale, numerotate de la
n+1 la 2n–1. Definim, pentru un arbore oarecare A de acest tip, lungimea externa ponderata:
unde ai este adancimea varfului i. Se observa ca numarul total de deplasari de elemente pentru strategia
corespunzatoare lui A este chiar L(A). Solutia optima a problemei noastre este atunci arborele (strategia)
pentru care lungimea externa ponderata este minima.
Proprietatea 11.1 Prin metoda greedy se obtine intotdeauna interclasarea optima a n siruri ordonate, deci
strategia cu arborele de lungime externa ponderata minima.
Demonstratie: Demonstram prin inductie. Pentru n = 1, proprietatea este verificata. Presupunem ca
proprietatea este adevarata pentru n–1 siruri. Fie A arborele strategiei greedy de interclasare a n siruri de
lungime q1 ≤ q2 ≤ ... qn. Fie B un arbore cu lungimea externa ponderata minima, corespunzator unei
strategii optime de interclasare a celor n siruri. In arborele A apare subarborele
reprezentand prima interclasare facuta conform strategiei greedy. In arborele B, fie un varf neterminal de
adancime maxima. Cei doi fii ai acestui varf sunt atunci doua varfuri terminale qj si qk. Fie B' arborele
obtinut din B schimband intre ele varfurile q1 si qj, respectiv q2 si qk. Evident, L(B') ≤ L(B). Deoarece B
are lungimea externa ponderata minima, rezulta ca L(B') = L(B). Eliminand din B' varfurile q1 si q2,
obtinem un arbore B" cu n–1 varfuri terminale q1+q2, q3, ..., qn. Arborele B' are lungimea externa
ponderata minima si L(B') = L(B") + q1+q2. Rezulta ca si B" are lungimea externa ponderata minima.
Atunci, conform ipotezei inductiei, avem L(B") = L(A'), unde A' este arborele strategiei greedy de
interclasare a sirurilor de lungime q1+q2, q3, ..., qn. Cum A se obtine din A' atasand la varful q1+q2 fiii q1 si
99

98. q2, iar B' se obtine in acelasi mod din B", rezulta ca L(A) = L(B') = L(B). Proprietatea este deci adevarata
pentru orice n.
La scrierea algoritmului care genereaza arborele strategiei greedy de interclasare vom folosi un
min-heap. Fiecare element al min-heap-ului este o pereche (q, i) unde i este numarul unui varf din
arborele strategiei de interclasare, iar q este lungimea sirului pe care il reprezinta. Proprietatea de min-
heap se refera la valoarea lui q.
Algoritmul interopt va construi arborele strategiei greedy. Un varf i al arborelui va fi memorat in
trei locatii diferite continand:
LU[i] = lungimea sirului reprezentat de varf
ST[i] = numarul fiului stang
DR[i] = numarul fiului drept
procedure interopt(Q[1 .. n])
{construieste arborele strategiei greedy de interclasare
a sirurilor de lungimi Q[i] = qi, 1 ≤ i ≤ n}
H ← min-heap vid
for i ← 1 to n do
(Q[i], i) => H {insereaza in min-heap}
LU[i] ← Q[i]; ST[i] ← 0; DR[i] ← 0
for i ← n+1 to 2n–1 do
(s, j) <= H {extrage radacina lui H}
(r, k) <= H {extrage radacina lui H}
ST[i] ← j; DR[i] ← k; LU[i] ← s+r
(LU[i], i) => H {insereaza in min-heap}
In cazul cel mai nefavorabil, operatiile de inserare in min-heap si de extragere din min-heap
necesita un timp in ordinul lui log n. Restul operatiilor necesita un timp constant. Timpul total pentru
interopt este deci in O(n log n).
Coduri Huffman
O alta aplicatie a strategiei greedy si a arborilor binari cu lungime externa ponderata minima este
obtinerea unei codificari cat mai compacte a unui text.
Un principiu general de codificare a unui sir de caractere este urmatorul: se masoara frecventa de
aparitie a diferitelor caractere dintr-un esantion de text si se atribuie cele mai scurte coduri, celor mai
frecvente caractere, si cele mai lungi coduri, celor mai putin frecvente caractere. Acest principiu sta, de
exemplu, la baza codului Morse. Pentru situatia in care codificarea este binara, exista o metoda eleganta
pentru a obtine codul respectiv. Aceasta metoda, descoperita de Huffman (1952) foloseste o strategie
greedy si se numeste codificarea Huffman. O vom descrie pe baza unui exemplu.
Fie un text compus din urmatoarele litere (in paranteze figureaza frecventele lor de aparitie):
S (10), I (29), P (4), O (9), T (5)
Conform metodei greedy, construim un arbore binar fuzionand cele doua litere cu frecventele cele
mai mici. Valoarea fiecarui varf este data de frecventa pe care o reprezinta.
Etichetam muchia stanga cu 1 si muchia dreapta cu 0. Rearanjam tabelul de frecvente:
S (10), I (29), O (9), {P, T} (45 = 9)
100

99. Multimea {P, T} semnifica evenimentul reuniune a celor doua evenimente independente
corespunzatoare aparitiei literelor P si T. Continuam procesul, obtinand arborele
In final, ajungem la arborele din Figura 11.3, in care fiecare varf terminal corespunde unei litere
din text.
Pentru a obtine codificarea binara a literei P, nu avem decat sa scriem secventa de 0-uri si 1-uri in
ordinea aparitiei lor pe drumul de la radacina catre varful corespunzator lui P: 1011. Procedam similar si
pentru restul literelor:
S (11), I (0), P (1011), O (100), T (1010)
Pentru un text format din n litere care apar cu frecventele f1, f2, ..., fn, un arbore de codificare este
un arbore binar cu varfurile terminale avand valorile f1, f2, ..., fn, prin care se obtine o codificare binara a
textului. Un arbore de codificare nu trebuie in mod necesar sa fie construit dupa metoda greedy a lui
Huffman, alegerea varfurilor care sunt fuzionate la fiecare pas putandu-se face dupa diverse criterii.
Lungimea externa ponderata a unui arbore de codificare este:
Figura 11.3 Arborele de codificare Huffman.
unde ai este adincimea varfului terminal corespunzator literei i. Se observa ca lungimea externa ponderata
este egala cu numarul total de caractere din codificarea textului considerat. Codificarea cea mai compacta
a unui text corespunde deci arborelui de codificare de lungime externa ponderata minima. Se poate
demonstra ca arborele de codificare Huffman minimizeaza lungimea externa ponderata pentru toti arborii
de codificare cu varfurile terminale avand valorile f1, f2, ..., fn. Prin strategia greedy se obtine deci
intotdeauna codificarea binara cea mai compacta a unui text.
Arborii de codificare pe care i-am considerat in acesta sectiune corespund unei codificari de tip
special: codificarea unei litere nu este prefixul codificarii nici unei alte litere. O astfel de codificare este
de tip prefix. Codul Morse nu face parte din aceasta categorie. Codificarea cea mai compacta a unui sir de
caractere poate fi intotdeauna obtinuta printr-un cod de tip prefix. Deci, concentrandu-ne atentia asupra
acestei categorii de coduri, nu am pierdut nimic din generalitate.
11.4 Arbori parţiali de cost minim
Fie G = <V, M> un graf neorientat conex, unde V este multimea varfurilor si M este multimea
muchiilor. Fiecare muchie are un cost nenegativ (sau o lungime nenegativa). Problema este sa gasim o
submultime A ⊆ M, astfel incat toate varfurile din V sa ramina conectate atunci cand sunt folosite doar
muchii din A, iar suma lungimilor muchiilor din A sa fie cat mai mica. Cautam deci o submultime A de
101

100. cost total minim. Aceasta problema se mai numeste si problema conectarii oraselor cu cost minim, avand
numeroase aplicatii.
Graful partial <V, A> este un arbore si este numit arborele partial de cost minim al grafului G
(minimal spanning tree). Un graf poate avea mai multi arbori partiali de cost minim si acest lucru se poate
verifica pe un exemplu.
Vom prezenta doi algoritmi greedy care determina arborele partial de cost minim al unui graf. In
terminologia metodei greedy, vom spune ca o multime de muchii este o solutie, daca constituie un arbore
partial al grafului G, si este fezabila, daca nu contine cicluri. O multime fezabila de muchii este
promitatoare, daca poate fi completata pentru a forma solutia optima. O muchie atinge o multime data de
varfuri, daca exact un capat al muchiei este in multime. Urmatoarea proprietate va fi folosita pentru a
demonstra corectitudinea celor doi algoritmi.
Proprietatea 11.2 Fie G = <V, M> un graf neorientat conex in care fiecare muchie are un cost nenegativ.
Fie W ⊂ V o submultime stricta a varfurilor lui G si fie A ⊆ M o multime promitatoare de muchii, astfel
incat nici o muchie din A nu atinge W. Fie m muchia de cost minim care atinge W. Atunci, A ∪ {m} este
promitatoare.
Demonstratie: Fie B un arbore partial de cost minim al lui G, astfel incat A ⊆ B (adica, muchiile din A
sunt continute in arborele B). Un astfel de B trebuie sa existe, deoarece A este promitatoare. Daca m ∈ B,
nu mai ramane nimic de demonstrat. Presupunem ca m ∉ B. Adaugandu-l pe m la B, obtinem exact un
ciclu. In acest ciclu, deoarece m atinge W, trebuie sa mai existe cel putin o muchie m' care atinge si ea pe
W (altfel, ciclul nu se inchide). Eliminandu-l pe m', ciclul dispare si obtinem un nou arbore partial B' al lui
G. Costul lui m este mai mic sau egal cu costul lui m', deci costul total al lui B' este mai mic sau egal cu
costul total al lui B. De aceea, B' este si el un arbore partial de cost minim al lui G, care include pe m.
Observam ca A ⊆ B' deoarece muchia m', care atinge W, nu poate fi in A. Deci, A ∪ {m} este
promitatoare.
Multimea initiala a candidatilor este M. Cei doi algoritmi greedy aleg muchiile una cate una intr-o
anumita ordine, aceasta ordine fiind specifica fiecarui algoritm.
Algoritmul lui Kruskal
Arborele partial de cost minim poate fi construit muchie, cu muchie, dupa urmatoarea metoda a lui
Kruskal (1956): se alege intai muchia de cost minim, iar apoi se adauga repetat muchia de cost minim
nealeasa anterior si care nu formeaza cu precedentele un ciclu. Alegem astfel #V–1 muchii. Este usor de
dedus ca obtinem in final un arbore. Este insa acesta chiar arborele partial de cost minim cautat?
Inainte de a raspunde la intrebare, sa consideram, de exemplu, graful din Figura 11.4a. Ordonam
crescator (in functie de cost) muchiile grafului: {1, 2}, {2, 3}, {4, 5}, {6, 7}, {1, 4}, {2, 5}, {4, 7}, {3, 5},
{2, 4}, {3, 6}, {5, 7}, {5, 6} si apoi aplicam algoritmul. Structura componentelor conexe este ilustrata,
pentru fiecare pas, in Tabelul 11.1.
102

101. Figura 11.4 Un graf si arborele sau partial de cost minim.
Pasul Muchia considerata Componentele conexe ale
subgrafului <V, A>
initializare — {1}, {2}, {3}, {4}, {5}, {6}, {7}
1 {1, 2} {1, 2}, {3}, {4}, {5}, {6}, {7}
2 {2, 3} {1, 2, 3}, {4}, {5}, {6}, {7}
3 {4, 5} {1, 2, 3}, {4, 5}, {6}, {7}
4 {6, 7} {1, 2, 3}, {4, 5}, {6, 7}
5 {1, 4} {1, 2, 3, 4, 5}, {6, 7}
6 {2, 5} respinsa (formeaza ciclu)
7 {4, 7} {1, 2, 3, 4, 5, 6, 7}
Tabelul 11.1 Algoritmul lui Kruskal aplicat grafului din Figura
11.4a.
Multimea A este initial vida si se completeaza pe parcurs cu muchii acceptate (care nu formeaza
un ciclu cu muchiile deja existente in A). In final, multimea A va contine muchiile {1, 2}, {2, 3}, {4, 5},
{6, 7}, {1, 4}, {4, 7}. La fiecare pas, graful partial <V, A> formeaza o padure de componente conexe,
obtinuta din padurea precedenta unind doua componente. Fiecare componenta conexa este la randul ei un
arbore partial de cost minim pentru varfurile pe care le conecteaza. Initial, fiecare varf formeaza o
componenta conexa. La sfarsit, vom avea o singura componenta conexa, care este arborele partial de cost
minim cautat (Figura 11.4b).
Ceea ce am observat in acest caz particular este valabil si pentru cazul general, din Proprietatea
11.2 rezultand:
Proprietatea 11.3 In algoritmul lui Kruskal, la fiecare pas, graful partial <V, A> formeaza o padure de
componente conexe, in care fiecare componenta conexa este la randul ei un arbore partial de cost minim
pentru varfurile pe care le conecteaza. In final, se obtine arborele partial de cost minim al grafului G.
Pentru a implementa algoritmul, trebuie sa putem manipula submultimile formate din varfurile
componentelor conexe. Folosim pentru aceasta o structura de multimi disjuncte si procedurile de tip find
si merge. In acest caz, este preferabil sa reprezentam graful ca o lista de muchii cu costul asociat lor,
astfel incat sa putem ordona aceasta lista in functie de cost. Iata algoritmul:
function Kruskal(G = <V, M>)
{initializare}
sorteaza M crescator in functie de cost
n ← #V
A←ø {va contine muchiile arborelui partial de cost minim}
initializeaza n multimi disjuncte continand
fiecare cate un element din V
{bucla greedy}
repeat
{u, v} ← muchia de cost minim care
inca nu a fost considerate
ucomp ← find(u)
vcomp ← find(v)
if ucomp ≠ vcomp then merge(ucomp, vcomp)
A ← A ∪ {{u, v}}
until #A = n-1
103

102. return A
Pentru un graf cu n varfuri si m muchii, presupunand ca se folosesc procedurile find3 si merge3,
numarul de operatii pentru cazul cel mai nefavorabil este in:
 O(m log m) pentru a sorta muchiile. Deoarece m ≤ n(n–1)/2, rezulta O(m log m) ⊆
O(m log n). Mai mult, graful fiind conex, din n-1 ≤ m rezulta si O(m log n) ⊆ O(m log m),
deci O(m log m) = O(m log n).
 O(n) pentru a initializa cele n multimi disjuncte.
 Cele cel mult 2m operatii find3 si n–1 operatii merge3 necesita un timp in O((2m+n-
1) lg* n). Deoarece O(lg* n) ⊆ O(log n) si n-1 ≤ m, acest timp este si in O(m log n).
 O(m) pentru restul operatiilor.
Deci, pentru cazul cel mai nefavorabil, algoritmul lui Kruskal necesita un timp in O(m log n).
O alta varianta este sa pastram muchiile intr-un min-heap. Obtinem astfel un nou algoritm, in care
initializarea se face intr-un timp in O(m), iar fiecare din cele n–1 extrageri ale unei muchii minime se face
intr-un timp in O(log m) = O(log n). Pentru cazul cel mai nefavorabil, ordinul timpului ramane acelasi cu
cel al vechiului algoritm. Avantajul folosirii min-heap-ului apare atunci cand arborele partial de cost
minim este gasit destul de repede si un numar considerabil de muchii raman netestate. In astfel de situatii,
algoritmul vechi pierde timp, sortand in mod inutil si aceste muchii.
Algoritmul lui Prim
Cel de-al doilea algoritm greedy pentru determinarea arborelui partial de cost minim al unui graf
se datoreaza lui Prim (1957). In acest algoritm, la fiecare pas, multimea A de muchii alese impreuna cu
multimea U a varfurilor pe care le conecteaza formeaza un arbore partial de cost minim pentru subgraful
<U, A> al lui G. Initial, multimea U a varfurilor acestui arbore contine un singur varf oarecare din V, care
va fi radacina, iar multimea A a muchiilor este vida. La fiecare pas, se alege o muchie de cost minim, care
se adauga la arborele precedent, dand nastere unui nou arbore partial de cost minim (deci, exact una dintre
extremitatile acestei muchii este un varf in arborele precedent). Arborele partial de cost minim creste
“natural”, cu cate o ramura, pina cand va atinge toate varfurile din V, adica pina cand U = V. Functionarea
algoritmului, pentru exemplul din Figura 11.4a, este ilustrata in Tabelul 11.2. La sfarsit, A va contine
aceleasi muchii ca si in cazul algoritmului lui Kruskal. Faptul ca algoritmul functioneaza intotdeauna
corect este exprimat de urmatoarea proprietate, pe care o puteti demonstra folosind Proprietatea 11.2.
Pasul Muchia considerata U
initializare — {1}
1 {2, 1} {1, 2}
2 {3, 2} {1, 2, 3}
3 {4, 1} {1, 2, 3, 4}
4 {5, 4} {1, 2, 3, 4, 5}
5 {7, 4} {1, 2, 3, 4, 5, 6}
6 {6, 7} {1, 2, 3, 4, 5, 6, 7}
Tabelul 11.2 Algoritmul lui Prim aplicat grafului din Figura 11.4a.
Proprietatea 11.4 In algoritmul lui Prim, la fiecare pas, <U, A> formeaza un arbore partial de cost minim
pentru subgraful <U, A> al lui G. In final, se obtine arborele partial de cost minim al grafului G.
Descrierea formala a algoritmului este data in continuare.
function Prim-formal(G = <V, M>)
{initializare}
A ←ø {va contine muchiile arborelui partial de cost minim}
U ← {un varf oarecare din V}
104

103. {bucla greedy}
while U ≠ V do
gaseste {u, v} de cost minim astfel ca u ∈ V U si v ∈ U
A ← A ∪ {{u, v}}
U ← U ∪ {u}
return A
Pentru a obtine o implementare simpla, presupunem ca: varfurile din V sunt numerotate de la 1 la
n, V = {1, 2, ..., n}; matricea simetrica C da costul fiecarei muchii, cu C[i, j] = + ∞ , daca muchia {i, j} nu
exista. Folosim doua tablouri paralele. Pentru fiecare i ∈ V U, vecin[i] contine varful din U, care este
conectat de i printr-o muchie de cost minim; mincost[i] da acest cost. Pentru i ∈ U, punem mincost[i] = –
1. Multimea U, in mod arbitrar initializata cu {1}, nu este reprezentata explicit. Elementele vecin[1] si
mincost[1] nu se folosesc.
function Prim(C[1 .. n, 1 .. n])
{initializare; numai varful 1 este in U}
A←ø
for i ← 2 to n do vecin[i] ← 1
mincost[i] ← C[i, 1]
{bucla greedy}
repeat n–1 times
min ← + ∞
for j ← 2 to n do
if 0 < mincost[ j] < min then min ← mincost[ j]
k←j
A ← A ∪ {{k, vecin[k]}}
mincost[k] ← –1 {adauga varful k la U}
for j ← 2 to n do
if C[k, j] < mincost[ j] then mincost[ j] ← C[k, j]
vecin[ j] ← k
return A
Bucla principala se executa de n–1 ori si, la fiecare iteratie, buclele for din interior necesita un
timp in O(n). Algoritmul Prim necesita, deci, un timp in O(n2). Am vazut ca timpul pentru algoritmul lui
Kruskal este in O(m log n), unde m = #M. Pentru un graf dens (adica, cu foarte multe muchii), se deduce
ca m se apropie de n(n–1)/2. In acest caz, algoritmul Kruskal necesita un timp in O(n2 log n) si algoritmul
Prim este probabil mai bun. Pentru un graf rar (adica, cu un numar foarte mic de muchii), m se apropie de
n si algoritmul Kruskal necesita un timp in O(n log n), fiind probabil mai eficient decat algoritmul Prim.
11.5 Cele mai scurte drumuri care pleaca din acelasi punct
Fie G = <V, M> un graf orientat, unde V este multimea varfurilor si M este multimea muchiilor.
Fiecare muchie are o lungime nenegativa. Unul din varfuri este desemnat ca varf sursa. Problema este sa
determinam lungimea celui mai scurt drum de la sursa catre fiecare varf din graf.
Vom folosi un algoritm greedy, datorat lui Dijkstra (1959). Notam cu C multimea varfurilor
disponibile (candidatii) si cu S multimea varfurilor deja selectate. In fiecare moment, S contine acele
varfuri a caror distanta minima de la sursa este deja cunoscuta, in timp ce multimea C contine toate
celelalte varfuri. La inceput, S contine doar varful sursa, iar in final S contine toate varfurile grafului. La
fiecare pas, adaugam in S acel varf din C a carui distanta de la sursa este cea mai mica.
105

104. Spunem ca un drum de la sursa catre un alt varf este special, daca toate varfurile intermediare de-a
lungul drumului apartin lui S. Algoritmul lui Dijkstra lucreaza in felul urmator. La fiecare pas al
algoritmului, un tablou D contine lungimea celui mai scurt drum special catre fiecare varf al grafului.
Dupa ce adaugam un nou varf v la S, cel mai scurt drum special catre v va fi, de asemenea, cel mai scurt
dintre toate drumurile catre v. Cand algoritmul se termina, toate varfurile din graf sunt in S, deci toate
drumurile de la sursa catre celelalte varfuri sunt speciale si valorile din D reprezinta solutia problemei.
Presupunem, pentru simplificare, ca varfurile sunt numerotate, V = {1, 2, ..., n}, varful 1 fiind
sursa, si ca matricea L da lungimea fiecarei muchii, cu L[i, j] = + ∞ , daca muchia (i, j) nu exista. Solutia
se va construi in tabloul D[2 .. n]. Algoritmul este:
function Dijkstra(L[1 .. n, 1 .. n])
{initializare}
C ← {2, 3, ..., n} {S = V C exista doar implicit}
for i ← 2 to n do D[i] ← L[1, i]
{bucla greedy}
repeat n–2 times
v ← varful din C care minimizeaza D[v]
C ← C {v} {si, implicit, S ← S ∪ {v}}
for fiecare w ∈ C do
D[w] ← min(D[w], D[v]+L[v, w])
return D
Pentru graful din Figura 11.5, pasii algoritmului sunt prezentati in Tabelul 11.3.
Figura 11.5 Un graf orientat.
Pasul v C D
initializare — {2, 3, 4, 5} [50, 30, 100, 10]
1 5 {2, 3, 4} [50, 30, 20, 10]
2 4 {2, 3} [40, 30, 20, 10]
3 3 {2} [35, 30, 20, 10]
Tabelul 11.3 Algoritmul lui Dijkstra aplicat grafului din Figura 11.5.
Observam ca D nu se schimba daca mai efectuam o iteratie pentru a-l scoate si pe {2} din C. De
aceea, bucla greedy se repeta de doar n-2 ori.
Se poate demonstra urmatoarea proprietate:
Proprietatea 11.5. In algoritmul lui Dijkstra, daca un varf i
i) este in S, atunci D[i] da lungimea celui mai scurt drum de la sursa catre i;
ii) nu este in S, atunci D[i] da lungimea celui mai scurt drum special de la sursa catre i.
106

105. La terminarea algoritmului, toate varfurile grafului, cu exceptia unuia, sunt in S. Din proprietatea
precedenta, rezulta ca algoritmul lui Dijkstra functioneaza corect.
Daca dorim sa aflam nu numai lungimea celor mai scurte drumuri, dar si pe unde trec ele, este
suficient sa adaugam un tablou P[2 .. n], unde P[v] contine numarul nodului care il precede pe v in cel
mai scurt drum. Pentru a gasi drumul complet, nu avem decat sa urmarim, in tabloul P, varfurile prin care
trece acest drum, de la destinatie la sursa. Modificarile in algoritm sunt simple:
– initializeaza P[i] cu 1, pentru 2 ≤ i ≤ n
– continutul buclei for cea mai interioara se inlocuieste cu
if D[w] > D[v] + L[v, w] then D[w] ← D[v] + L[v, w]
P[w] ← v
– bucla repeat se executa de n -1 ori
Sa presupunem ca aplicam algoritmul Dijkstra asupra unui graf cu n varfuri si m muchii.
Initializarea necesita un timp in O(n). Alegerea lui v din bucla repeat presupune parcurgerea tuturor
varfurilor continute in C la iteratia respectiva, deci a n -1, n -2, ..., 2 varfuri, ceea ce necesita in total un
timp in O(n2). Bucla for interioara efectueaza n-2, n-3, ..., 1 iteratii, totalul fiind tot in O(n2). Rezulta ca
algoritmul Dijkstra necesita un timp in O(n2).
Incercam sa imbunatatim acest algoritm. Vom reprezenta graful nu sub forma matricii de
adiacenta L, ci sub forma a n liste de adiacenta, continand pentru fiecare varf lungimea muchiilor care
pleaca din el. Bucla for interioara devine astfel mai rapida, deoarece putem sa consideram doar varfurile
w adiacente lui v. Aceasta nu poate duce la modificarea ordinului timpului total al algoritmului, daca nu
reusim sa scadem si ordinul timpului necesar pentru alegerea lui v din bucla repeat. De aceea, vom tine
varfurile v din C intr-un min-heap, in care fiecare element este de forma (v, D[v]), proprietatea de min-
heap referindu-se la valoarea lui D[v]. Numim algoritmul astfel obtinut Dijkstra-modificat. Sa il analizam
in cele ce urmeaza.
Initializarea min-heap-ului necesita un timp in O(n). Instructiunea “C ← C {v}” consta in
extragerea radacinii min-heap-ului si necesita un timp in O(log n). Pentru cele n–2 extrageri este nevoie
de un timp in O(n log n).
Pentru a testa daca “D[w] > D[v]+L[v, w]”, bucla for interioara consta acum in inspectarea
fiecarui varf w din C adiacent lui v. Fiecare varf v din C este introdus in S exact o data si cu acest prilej
sunt testate exact muchiile adiacente lui; rezulta ca numarul total de astfel de testari este de cel mult m.
Daca testul este adevarat, trebuie sa il modificam pe D[w] si sa operam un percolate cu w in min-heap,
ceea ce necesita din nou un timp in O(log n). Timpul total pentru operatiile percolate este deci in
O(m log n).
In concluzie, algoritmul Dijkstra-modificat necesita un timp in O(max(n, m) log n). Daca graful
este conex, atunci m ≥ n si timpul este in O(m log n). Pentru un graf rar este preferabil sa folosim
algoritmul Dijkstra-modificat, iar pentru un graf dens algoritmul Dijkstra este mai eficient.
Este usor de observat ca, intr-un graf G neorientat conex, muchiile celor mai scurte drumuri de la
un varf i la celelalte varfuri formeaza un arbore partial al celor mai scurte drumuri pentru G. Desigur,
acest arbore depinde de alegerea radacinii i si el difera, in general, de arborele partial de cost minim al lui
G.
Problema gasirii celor mai scurte drumuri care pleaca din acelasi punct se poate pune si in cazul
unui graf neorientat.
11.6 Euristica greedy
Pentru anumite probleme, se poate accepta utilizarea unor algoritmi despre care nu se stie daca
furnizeaza solutia optima, dar care furnizeaza rezultate “acceptabile”, sunt mai usor de implementat si
mai eficienti decat algoritmii care dau solutia optima. Un astfel de algoritm se numeste euristic.
Una din ideile frecvent utilizate in elaborarea algoritmilor euristici consta in descompunerea
procesului de cautare a solutiei optime in mai multe subprocese succesive, fiecare din aceste subprocese
constand dintr-o optimizare. O astfel de strategie nu poate conduce intotdeauna la o solutie optima,
107

106. deoarece alegerea unei solutii optime la o anumita etapa poate impiedica atingerea in final a unei solutii
optime a intregii probleme; cu alte cuvinte, optimizarea locala nu implica, in general, optimizarea globala.
Regasim, de fapt, principiul care sta la baza metodei greedy. Un algoritm greedy, despre care nu se poate
demonstra ca furnizeaza solutia optima, este un algoritm euristic.
Vom da doua exemple de utilizare a algoritmilor greedy euristici.
11.6.1 Colorarea unui graf
Fie G = <V, M> un graf neorientat, ale carui varfuri trebuie colorate astfel incat oricare doua
varfuri adiacente sa fie colorate diferit. Problema este de a obtine o colorare cu un numar minim de culori.
Folosim urmatorul algoritm greedy: alegem o culoare si un varf arbitrar de pornire, apoi consideram
varfurile ramase, incercand sa le coloram, fara a schimba culoarea. Cand nici un varf nu mai poate fi
colorat, schimbam culoarea si varful de start, repetand procedeul.
Figura 11.6 Un graf care va fi colorat.
Daca in graful din Figura 11.6 pornim cu varful 1 si il coloram in rosu, mai putem colora tot in
rosu varfurile 3 si 4. Apoi, schimbam culoarea si pornim cu varful 2, colorandu-l in albastru. Mai putem
colora cu albastru si varful 5. Deci, ne-au fost suficiente doua culori. Daca coloram varfurile in ordinea 1,
5, 2, 3, 4, atunci se obtine o colorare cu trei culori.
Rezulta ca, prin metoda greedy, nu obtinem decat o solutie euristica, care nu este in mod necesar
solutia optima a problemei. De ce suntem atunci interesati intr-o astfel de rezolvare? Toti algoritmii
cunoscuti, care rezolva optim aceasta problema, sunt exponentiali, deci, practic, nu pot fi folositi pentru
cazuri mari. Algoritmul greedy euristic propus furnizeaza doar o solutie “acceptabila”, dar este simplu si
eficient.
Un caz particular al problemei colorarii unui graf corespunde celebrei probleme a colorarii
hartilor: o harta oarecare trebuie colorata cu un numar minim de culori, astfel incat doua tari cu frontiera
comuna sa fie colorate diferit. Daca fiecarui varf ii corespunde o tara, iar doua varfuri adiacente
reprezinta tari cu frontiera comuna, atunci hartii ii corespunde un graf planar, adica un graf care poate fi
desenat in plan fara ca doua muchii sa se intersecteze. Celebritatea problemei consta in faptul ca, in toate
exemplele intalnite, colorarea s-a putut face cu cel mult 4 culori. Aceasta in timp ce, teoretic, se putea
demonstra ca pentru o harta oarecare este nevoie de cel mult 5 culori.
Problema colorarii unui graf poate fi interpretata si in contextul planificarii unor activitati. De
exemplu, sa presupunem ca dorim sa executam simultan o multime de activitati, in cadrul unor sali de
clasa. In acest caz, varfurile grafului reprezinta activitati, iar muchiile unesc activitatile incompatibile.
Numarul minim de culori necesare pentru a colora graful corespunde numarului minim de sali necesare.
11.6.2 Problema comis-voiajorului
Se cunosc distantele dintre mai multe orase. Un comis-voiajor pleaca dintr-un oras si doreste sa se
intoarca in acelasi oras, dupa ce a vizitat fiecare din celelalte orase exact o data. Problema este de a
minimiza lungimea drumului parcurs. Si pentru aceasta problema, toti algoritmii care gasesc solutia
optima sunt exponentiali.
108

107. Problema poate fi reprezentata printr-un graf neorientat, in care oricare doua varfuri diferite ale
grafului sunt unite intre ele printr-o muchie, de lungime nenegativa. Cautam un ciclu de lungime minima,
care sa se inchida in varful initial si care sa treaca prin toate varfurile grafului.
Conform strategiei greedy, vom construi ciclul pas cu pas, adaugand la fiecare iteratie cea mai
scurta muchie disponibila cu urmatoarele proprietati:
• nu formeaza un ciclu cu muchiile deja selectate (exceptand pentru ultima muchie aleasa,
care completeaza ciclul)
• nu exista inca doua muchii deja selectate, astfel incat cele trei muchii sa fie incidente in
acelasi varf
La: 2 3 4 5 6
De la:
1 3 10 11 7 25
2 6 12 8 26
3 9 4 20
4 5 15
5 18
Tabelul 11.4 Matricea distantelor pentru problema comis-voiajorului.
De exemplu, pentru sase orase a caror matrice a distantelor este data in Tabelul 11.4, muchiile se
aleg in ordinea: {1, 2}, {3, 5}, {4, 5}, {2, 3}, {4, 6}, {1, 6} si se obtine ciclul (1, 2, 3, 5, 4, 6, 1) de
lungime 58. Algoritmul greedy nu a gasit ciclul optim, deoarece ciclul (1, 2, 3, 6, 4, 5, 1) are lungimea 56.
109

108. CAPITOLUL XII
STUDII DE CAZ – APLICAŢII
110

109. 1. Să se determine toate numerele perechile de numere gemene pana la o anumita valoare n. Două
numere sunt gemene dacă sunt ambele prime şi diferenţa dintre cel mai mare şi cel mai mic este 2.
Private Sub CommandButton1_Click()
Dim rad As Integer, n As Integer, p As Integer, i As Integer, j
As Integer
cit_n "n = ", n
For i = 3 To n
p = 1
rad = Int(Sqr(i + 2))
For j = 2 To Int(rad)
If i Mod j = 0 Or (i + 2) Mod j = 0 Then
prim = 0
j = Int(rad)
End If
Next
If p Then
MsgBox "(" + Str$(i) + "," + Str$(i + 2) + ")" + Chr(13)
End If
Next
End Sub
2. Să se citească o valoare naturala n cu valori cuprinse intre 1 şi 100.
Sub cit_n(mes As String, nnn As Integer)
Do
nnn = InputBox(mes, y)
Loop Until n > 0 And n < 100
End Sub
3. Citirea unui vector cu n componente
Sub cit_date(mes As String, n As Integer, a As vector)
For i = 1 To n
111

110. a.v(i) = InputBox(mes + "(" + Str$(i) + ")=", y)
Next
End Sub
4. Tipărirea unui tablou cu n componente
Sub tipar(mes As String, n As Integer, a As vector)
sir = ""
For i = 1 To n
sir = sir + Str$(a.v(i)) + ","
Next
MsgBox mes + " " + sir
End Sub
5. Generarea permutărilor utilizănd metoda backtracking
Private Sub CommandButton14_Click()
cit_n "n = ", n
back_perm
End Sub
6. Generarea produsului cartezian a n mulţimi utilizând metoda backtracking
Private Sub CommandButton16_Click()
Dim a As vector
cit_n "n=", n
cit_date "a", n, a
tipar " multimile sunt : ", n, a
back_prod_cart
End Sub
7. Generarea permutărilor utilizănd metoda backtracking
Private Sub CommandButton17_Click()
cit_n "n = ", n
cit_n "p = ", p
back_aranj
End Sub
8. “Problema celor n dame” utilizănd metoda backtracking
Private Sub CommandButton15_Click()
cit_n "n = ", n
back
End Sub
9. Generarea combinărilor (de n luate câte m) utilizănd metoda backtracking
Private Sub CommandButton18_Click()
cit_n "n = ", n
cit_n "p = ", p
back_comb
End Sub
10. Generarea partiţiilor unei mulţimi utilizănd metoda backtracking
Private Sub CommandButton19_Click()
112

111. cit_n "n=", n
back_partitii
End Sub
11. Căutarea binară utilizând metoda “Divide et Impera” pentru sortarea unui şir de numere
Private Sub CommandButton2_Click()
Dim n As Integer, x As Integer, a As vector
cit_n "n = ", n
cit_date "a", n, a
tipar "sirul dat este : ", n, a
divimp 1, n, a
'MsgBox "Sirul a sortat este"
tipar "Sirul a sortat este", n, a
x = InputBox(" x = ", y)
st = 1
dr = n
l = True
While st <= dr And l = True
pp = (st + dr) / 2
If a.v(pp) = x Then
l = False
MsgBox "numarul x = " + Str$(x) + " se afla printre elementele
vectorului a"
End If
If a.v(pp) < x Then
st = pp + 1
Else
dr = p - 1
End If
Wend
If l = True Then
MsgBox "numarul x = " + Str$(x) + " nu se fala in sir "
End If
End Sub
12. Realizarea unei subrutine pentru sortarea rapidă “Quicksort”
Sub sort(p As Integer, q As Integer, a As vector)
Dim m As Integer
If a.v(p) > a.v(q) Then
m = a.v(p)
a.v(p) = a.v(q)
a.v(q) = m
End If
End Sub
13. Sortarea “Merge-Sort” utilizând metoda “Divide et impera”
Sub interc(p As Integer, q As Integer, m As Integer, a As vector)
Dim b As vector, i, j, k As Integer
i = p
j = m + 1
k = 1
While (i <= m) And (j <= q)
If a.v(i) <= a.v(j) Then
b.v(k) = a.v(i)
113

112. i = i + 1
k = k + 1
Else
b.v(k) = a.v(j)
j = j + 1
k = k + 1
End If
Wend
If i <= m Then
For j = i To m
b.v(k) = a.v(j)
k = k + 1
Next
Else
For i = j To q
b.v(k) = a.v(i)
k = k + 1
Next
End If
k = 1
For i = p To q
a.v(i) = b.v(k)
k = k + 1
Next
End Sub
14. Sortarea rapidă utilizând metoda “Divide et impera”
Sub divimp(p As Integer, q As Integer, a As vector)
Dim m As Integer
If (q - p) <= 1 Then
sort p, q, a
Else
m = Int((p + q) / 2)
divimp p, m, a
divimp m + 1, q, a
interc p, q, m, a
End If
End Sub
15. Problema colorării hărţilor utilizând metoda backtracking
Private Sub CommandButton20_Click()
Dim mat As matrice
cit_n " n = ", n
cit_mat "a", n, n, mat
tipar_mat "a", n, n, mat
For i = 1 To n
For j = 1 To n
mat.m(j, i) = mat.m(i, j)
Next
Next
back_col
End Sub
114

113. 16. Interclasarea a 2 şiruri ordonate crescător
Private Sub CommandButton3_Click()
Dim n As Integer, x As Integer, a As vector, m As Integer, b As
vector, k As Integer, c As vector
cit_n "n = ", n
cit_date "a", n, a
tipar "sirul dat este : ", n, a
divimp 1, n, a
'MsgBox "Sirul a sortat este"
tipar "Sirul a sortat este", n, a
cit_n "m = ", m
cit_date "a", m, b
tipar "sirul dat este : ", m, b
divimp 1, m, b
'MsgBox "Sirul a sortat este"
tipar "Sirul b sortat este", m, b
i = 1
j = 1
k = 0
While i <= n And j <= m
If a.v(i) < b.v(j) Then
k = k + 1
c.v(k) = a.v(i)
i = i + 1
Else
If a.v(i) = b.v(j) Then
k = k + 1
c.v(k) = a.v(i)
i = i + 1
j = j + 1
Else
k = k + 1
c.v(k) = b.v(j)
j = j + 1
End If
End If
Wend
If i <= n Then
For l = i To n
k = k + 1
c.v(k) = a.v(l)
Next
End If
If j <= m Then
For l = j To m
k = k + 1
c.v(k) = b.v(l)
Next
End If
tipar "A U B = ", k, c
End Sub
17. Sortarea Shell-Sort utilizând metoda Greedy
Private Sub CommandButton4_Click()
Dim n As Integer, k As Integer, a As vector
115

114. cit_n "n = ", n
cit_date "a", n, a
tipar "sirul dat este : ", n, a
k = n
Do
k = k / 2
Do
b = 1
For i = 1 To n - k
If a.v(i) > a.v(i + k) Then
x = a.v(i)
a.v(i) = a.v(i + k)
a.v(i + k) = x
b = 0
End If
Next
Loop Until Not (b = 0)
Loop Until Not (k <> 1)
'MsgBox "Sirul a sortat este"
tipar "Sirul a sortat este", n, a
End Sub
18. Citirea si scrierea unei matrici pe ecran
Private Sub CommandButton5_Click()
Dim n As Integer, m As Integer, a As matrice, b As matrice, p As
Integer, c As matrice
cit_n "n = ", n
cit_n "m = ", m
cit_mat "a", n, m, a
tipar_mat "a", n, m, a
End Sub
19. Citirea unei matrici de pe dispozitivul de intrare
Sub cit_mat(mes As String, n As Integer, m As Integer, a As
matrice)
For i = 1 To n
For j = 1 To m
a.m(i, j) = InputBox(mes + "(" + Str$(i) + "," + Str$(j) +
")=", y)
Next
Next
End Sub
20. Scrierea unei matrici pe ecran
Sub tipar_mat(mes As String, n As Integer, m As Integer, a As
matrice)
sir = mes + Chr(10)
For i = 1 To n
For j = 1 To m
sir = sir + Str$(a.m(i, j)) + " "
Next
sir = sir + Chr(10)
Next
MsgBox sir
116

115. End Sub
21. Produsul a două matrici
Private Sub CommandButton6_Click()
Dim n As Integer, m As Integer, a As matrice, b As matrice, p As
Integer, c As matrice
cit_n "n = ", n
cit_n "m = ", m
cit_mat "a", n, m, a
tipar_mat "a", n, m, a
cit_n "p = ", p
'cit_n "m = ", m
cit_mat "b", m, p, b
tipar_mat "m", m, p, b
prod_mat n, m, p, a, b, c
tipar_mat "axb=", n, p, c
End Sub
Sub prod_mat(n As Integer, m As Integer, p As Integer, a As
matrice, b As matrice, c As matrice)
For i = 1 To n
For j = 1 To p
c.m(i, j) = 0
For k = 1 To m
c.m(i, j) = c.m(i, j) + a.m(i, k) * b.m(k, j)
Next
Next
Next
End Sub
22. Programul principal pentru adunarea a două matrici
Private Sub CommandButton7_Click()
Dim n As Integer, m As Integer, a As matrice, b As matrice, p As
Integer, c As matrice
cit_n "n = ", n
cit_n "m = ", m
cit_mat "a", n, m, a
tipar_mat "a", n, m, a
'cit_n "p = ", p
'cit_n "m = ", m
cit_mat "b", n, m, b
tipar_mat "b", n, m, b
ad_mat n, m, a, b, c
tipar_mat "a+b=", n, m, c
End Sub
23. Subrutina pentru adunarea a două matrici
Sub ad_mat(n As Integer, m As Integer, a As matrice, b As matrice,
c As matrice)
For i = 1 To n
For j = 1 To m
c.m(i, j) = a.m(i, j) + b.m(i, j)
Next
Next
117

116. End Sub
24. Programul principal pentru scăderea a două matrici
Private Sub CommandButton8_Click()
Dim n As Integer, m As Integer, a As matrice, b As matrice, p As
Integer, c As matrice
cit_n "n = ", n
cit_n "m = ", m
cit_mat "a", n, m, a
tipar_mat "a", n, m, a
'cit_n "p = ", p
'cit_n "m = ", m
cit_mat "b", n, m, b
tipar_mat "b", n, m, b
scad_mat n, m, a, b, c
tipar_mat "a-b=", n, m, c
End Sub
25. Subrutina pentru adunarea a două matrici
Sub scad_mat(n As Integer, m As Integer, a As matrice, b As
matrice, c As matrice)
For i = 1 To n
For j = 1 To m
c.m(i, j) = a.m(i, j) - b.m(i, j)
Next
Next
End Sub
26. Programul principal pentru ridicarea unei matrici la o putere p
Private Sub CommandButton9_Click()
Dim n As Integer, m As Integer, a As matrice, b As matrice, p As
Integer, c As matrice, k As Integer
'Sub scad_mat(n As Integer, m As Integer, a As matrice, b As
matrice, c As matrice)
'const t as vector ={0,31,28,31,30,31,30,31,30,31,30,31,30}
cit_n "n = ", n
'cit_n "m = ", m
cit_mat "a", n, n, a
tipar_mat "a", n, n, a
cit_n "putere = ", k
'cit_n "m = ", m
'cit_mat "b", n, m, b
'tipar_mat "b", n, m, b
putere_mat n, a, k, c
tipar_mat "a^p=", n, n, c
End Sub
27. Subprogramul pentru ridicarea unei matrici la o putere p
Sub putere_mat(n As Integer, a As matrice, k As Integer, c As
matrice)
Dim b As matrice, c1 As matrice
For i = 1 To n
For j = 1 To n
118

117. c.m(i, j) = 0
c1.m(i, j) = 0
Next
Next
For i = 1 To n
c.m(i, i) = 1
c1.m(i, i) = 1
Next
'Next
While k > 0
If k Mod 2 = 1 Then
prod_mat n, n, n, c1, a, c
End If
For i = 1 To n
For j = 1 To n
c1.m(i, j) = c.m(i, j)
'c1.m(i, j) = 0
Next
Next
prod_mat n, n, n, a, a, b
k = Int(k / 2)
For i = 1 To n
For j = 1 To n
a.m(i, j) = b.m(i, j)
'c1.m(i, j) = 0
Next
Next
Wend
For i = 1 To n
For j = 1 To n
c.m(i, j) = c1.m(i, j)
'c1.m(i, j) = 0
Next
Next
End Sub
28. Subrutina de iniţializare a stivei pentru metoda backtracking
Sub init(k As Integer, st As stiva)
st.ss(k) = 0
End Sub
29. Subrutina successor pentru “problema celor n dame”
Sub succesor(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < n Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
30. Subrutina successor pentru generarea combinărilor
Sub succesor_c(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < n - p + k Then
119

118. am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
31. Subrutina succesor pentru problema “produsului cartezian a n mulţimi” utilizând metoda
backtracking
Sub succesor_prod(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < a.v(k) Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
32. Subrutina successor pentru colorarea hărţilor
Sub succesor_col(am_suc As Boolean, st As stiva, k As Integer)
If st.ss(k) < 4 Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
33. Subrutina valid pentru “problema celor n dame”
Sub valid(ev As Boolean, st As stiva, k As Integer)
ev = True
For i = 1 To k - 1
If (st.ss(i) = st.ss(k)) Or (Abs(st.ss(i) - st.ss(k)) = Abs(k -
i)) Then
ev = False
End If
Next
End Sub
34. Subrutina valid pentru colorarea hărţilor
Sub valid_col(ev As Boolean, st As stiva, k As Integer)
ev = True
For i = 1 To k - 1
If (st.ss(i) = st.ss(k)) And (mat.m(i, k) = 1) Then
ev = False
End If
Next
End Sub
Sub valid_c(ev As Boolean, st As stiva, k As Integer)
Dim i As Integer
ev = True
For i = 1 To k - 1
120

119. If (st.ss(i) = st.ss(k)) Then
ev = False
End If
Next
If k > 1 Then
If st.ss(k) < st.ss(k - 1) Then
ev = False
End If
End If
End Sub
35. Subrutina valid pentru “produs cartezian a n mulţimi”
Sub valid_prod(ev As Boolean, st As stiva, k As Integer)
ev = True
End Sub
36. Subrutina soluţie pentru generarea permutărilor
Function solutie(k As Integer) As Boolean
If k = n Then
solutie = True
Else
solutie = False
End If
End Function
37. Subrutina soluţie pentru generarea aranjamentelor sau combinărilor
Function solutie1(k As Integer) As Boolean
If k = p Then
solutie1 = True
Else
solutie1 = False
End If
End Function
38. Subrutina tipărire pentru “problema celor n dame”
Sub tiparr()
Dim i As Integer, b As String
b = " "
For i = 1 To n
b = b + "(" + Str$(i) + "," + Str$(st.ss(i)) + "),"
Next
MsgBox b
End Sub
39. Subrutina tipărire pentru “colorarea hărţilor”
Sub tipar_col()
Dim i As Integer, b As String
b = " "
For i = 1 To n
b = b + "Tara = " + Str$(i) + "; culoarea " + Str$(st.ss(i)) + " "
Next
121

120. MsgBox b
End Sub
40. Subrutina back pentru “problema celor n dame”
Sub back()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor am_suc, st, k
If am_suc = True Then
valid ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tiparr
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
End Sub
41. Programul principal pentru “problema celor n dame”
Sub Button2_Click()
n = InputBox("n=", ib_title)
back
End Sub
42. Subrutina back pentru “generarea permutărilor”
Sub back_perm()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor am_suc, st, k
If am_suc = True Then
valid1 ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tipar_r
Else
k = k + 1
init k, st
End If
Else
122

121. k = k - 1
End If
Wend
End Sub
43. Subrutina back pentru “generarea aranjamentelor”
Sub back_aranj()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor am_suc, st, k
If am_suc = True Then
valid1 ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie1(k) Then
tipar_rr
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
End Sub
44. Subrutina valid pentru metoda backtracking
Sub valid1(ev As Boolean, st As stiva, k As Integer)
ev = True
For i = 1 To k - 1
If (st.ss(i) = st.ss(k)) Then
ev = False
End If
Next
End Sub
45. Subrutina tipar pentru metoda backtracking
Sub tipar_r()
Dim i As Integer, b As String
b = " "
For i = 1 To n
b = b + Str$(st.ss(i)) + ","
Next
MsgBox b
End Sub
46. Subrutina tipar pentru metoda backtracking
Sub tipar_rr()
Dim i As Integer, b As String
123

122. b = " "
For i = 1 To p
b = b + Str$(st.ss(i)) + ","
Next
MsgBox b
End Sub
47. Subrutina back pentru “generarea combinărilor”
Sub back_comb()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor_c am_suc, st, k
If am_suc = True Then
valid_c ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie1(k) Then
tipar_rr
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
End Sub
48. Subrutina back pentru “generarea produsului cartezian a n multimi”
Sub back_prod_cart()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor_prod am_suc, st, k
If am_suc = True Then
valid_prod ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tipar_r
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
124

123. End Sub
49. Subrutina back pentru “generarea partiţiilor unei mulţimi”
Sub back_partitii()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor_part am_suc, st, k
If am_suc = True Then
valid_prod ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tipar_part
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
End Sub
50. Subrutina tiparire pentru problema “generare partiţii” a unei mulţimi
Sub tipar_part()
Dim i As Integer, max As Integer, j As Integer, sir As String
sir = ""
max = st.ss(1)
For i = 2 To n
If max < st.ss(i) Then
max = st.ss(i)
End If
Next
sir = " PARTITII "
For j = 1 To max
For i = 1 To n
If st.ss(i) = j Then
sir = sir + Str$(i) + " "
End If
Next
sir = sir + Chr(10)
Next
MsgBox sir
End Sub
51. Subrutina succesor pentru problema “generare partiţii” a unei mulţimi
Sub succesor_part(am_suc As Boolean, st As stiva, k As Integer)
Dim i As Integer, max As Integer
If k = 1 Then
max = 1
125

124. Else
max = st.ss(1)
For i = 2 To k - 1
If max < st.ss(i) Then
max = st.ss(i)
End If
Next
End If
If st.ss(k) < max + 1 And st.ss(k) < k Then
am_suc = True
st.ss(k) = st.ss(k) + 1
Else
am_suc = False
End If
End Sub
52. Subrutina back pentru “colorarea hărţilor”
Sub back_col()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor_col am_suc, st, k
If am_suc = True Then
valid_col ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tipar_col
Else
k = k + 1
init k, st
End If
Else
k = k - 1
End If
Wend
End Sub
Public s As String
53. Funcţia pentru a verifica dacă un număr natural n este prim sau nu
Function prim(n As Integer) As Boolean
b = True
For i = 2 To Int(Sqr(n))
If n Mod i = 0 Then
b = False
i = Int(Sqr(n))
End If
Next
prim = b
End Function
54. Programul principal pentru inversarea unui număr natural n
126

125. Sub buton1_Click()
Dim n As Integer, ninv As Integer, n1 As Integer, sir As String
Do
n = InputBox(" n = ", y)
Loop Until n > 0
n1 = n
ninv = 0
sir = ""
While n <> 0
sir = sir + LTrim(RTrim(Str$(n Mod 10)))
ninv = ninv * 10 + n Mod 10
n = Int(n / 10)
Wend
MsgBox " numarul initial este : " + Str$(n1) + " numarul inversat
este: " + sir
End Sub
55. Algoritmul lui Euclid pentru calcularea CMMDC a două numere naturale pozitive
Private Sub Buton10_Click()
Dim a As Integer, b As Integer, c As Integer
Do
a = InputBox("a = ", y)
b = InputBox("b = ", y)
a1 = a
b1 = b
Loop Until a > 0 And b > 0 And a > b
c = euclid2(a, b)
If c = 1 Then
MsgBox " nr. sunt prime intre ele (" + Str$(a1) + "," + Str$(b1)
+ ")"
Else
MsgBox "Cmmdc (" + Str$(a1) + "," + Str$(b1) + ")=" + Str$
(euclid2(a, b))
End If
End Sub
56. Sortarea unui sir cu n componente utilizând metoda bulelor
Private Sub Buton11_Click()
Dim n As Integer, a As vector
cit_n "n = ", n
cit_date "a", n, a
tipar "vectorul initial a este ", n, a
bule n, a
tipar "vectorul a sortat este : ", n, a
End Sub
57. Subrutina pentru sortarea prin metoda bulelor
Sub bule(n As Integer, a As vector)
Do
k = 0
For i = 1 To n - 1
If a.v(i) > a.v(i + 1) Then
x = a.v(i)
127

126. a.v(i) = a.v(i + 1)
a.v(i + 1) = x
k = 1
End If
Next
Loop Until k = 0
End Sub
58. Sortarea unui sir cu n componente utilizând metoda selecţiei directe
Private Sub Buton12_Click()
Dim n As Integer, a As vector
cit_n "n = ", n
cit_date "a", n, a
tipar "vectorul initial a este ", n, a
selectie n, a
tipar "vectorul a sortat este : ", n, a
End Sub
59. Subrutina pentru sortarea prin metoda selecţiei directe
Sub selectie(n As Integer, a As vector)
For i = 1 To n - 1
min = a.v(i)
k = i
For j = i + 1 To n
If min > a.v(j) Then
min = a.v(j)
k = j
End If
Next
If k <> i Then
x = a.v(i)
a.v(i) = a.v(k)
a.v(k) = x
End If
Next
End Sub
60. Sortarea unui sir cu n componente utilizând metoda prin numărare
Private Sub Buton14_Click()
Dim n As Integer, a As vector
cit_n "n = ", n
cit_date "a", n, a
tipar "vectorul initial a este ", n, a
numarare n, a
tipar "vectorul a sortat este : ", n, a
End Sub
61. Suma cifrelor unui număr natural dat n
Sub buton2_Click()
Dim n As Integer, s As Long, n1 As Integer
Do
n = InputBox(" n = ", y)
Loop Until n > 0
128

127. n1 = n
s = 0
While n <> 0
s = s + n Mod 10
n = Int(n / 10)
Wend
MsgBox " suma cifrelor numarului n = " + Str$(n1) + " este : " +
Str$(s)
End Sub
62. Verificarea unui numar natural n daca este prim sau nu
Sub buton3_Click()
Dim n As Integer, s As Long, n1 As Integer
Do
n = InputBox(" n = ", y)
Loop Until n > 0
n1 = n
b = True
For i = 2 To Int(Sqr(n))
If n Mod i = 0 Then
b = False
i = Int(Sqr(n))
End If
Next
If b = True Then
MsgBox "numarul n = " + Str$(n) + " este prim"
Else
MsgBox "numarul n = " + Str$(n) + " nu este prim"
End If
End Sub
63. Determinarea numerelor prime mai mici sau egale cu n utilizând metoda directă
Sub buton4_Click()
Dim n As Integer, s As Long, n1 As Integer, i As Integer
Do
n = InputBox(" n = ", y)
Loop Until n > 0
n1 = n
If n = 2 Then
MsgBox "numerele prime sunt : 2"
Else
sir = "2,"
i = 3
While i <= n
If prim(i) = True Then
sir = sir + Str$(i) + ","
End If
i = i + 2
Wend
End If
MsgBox "numere prime sunt : " + sir
End Sub
64. Ciurul lui Eratostene
129

128. Sub buton5_Click()
Dim n As Integer, a As vector, sir As String
Do
n = InputBox(" n = ", y)
Loop Until n > 0
For i = 1 To n
a.v(i) = i
Next
For i = 2 To Int(Sqr(n))
If a.v(i) <> 0 Then
j = 2 * i
While j <= n
j = j + i
a.v(j) = 0
Wend
End If
Next
sir = ""
For i = 2 To n
If a.v(i) <> 0 Then
sir = sir + Str$(i) + ","
End If
Next
MsgBox "Numerele prime sunt : " + sir
End Sub
65. Descompunerea unui numar in factori primi
Sub buton6_Click()
Dim n As Integer, a As vector, sir As String, n1 As Integer
Do
n = InputBox(" n = ", y)
Loop Until n > 0
i = 2
n1 = n
l = 0
sir = ""
Do
fm = 0
While n Mod i = 0
fm = fm + 1
l = 1
n = Int(n / i)
Wend
If fm <> 0 Then
sir = sir + Str$(i) + "^" + Str$(fm) + "*"
End If
i = i + 1
Loop Until n = 1
If l = 0 Then
sir = Str$(n) + "^1"
End If
MsgBox Str$(n1) + "=" + sir
End Sub
66. Scrierea unui număr ca suma a două cuburi
130

129. Sub buton7_Click()
Dim n As Integer, a As vector, sir As String, n1 As Integer
Do
n = InputBox(" n = ", y)
Loop Until n > 0
n1 = n
For n = 1 To n1
Max = Int(n / 2)
nr = 0
For i = 1 To Max
For j = i To Max
If i * i * i + j * j * j = n Then
If nr = 0 Then
i1 = i
j1 = j
Else
i2 = i
j2 = j
End If
nr = nr + 1
End If
Next
Next
If nr > 1 Then
MsgBox Str$(n) + "=" + Str$(i1) + "^" + Str$(j1) + "+" + Str$
(i2) + "^" + Str$(j2)
End If
Next
End Sub
67. CMMDC a două numere utilizând recursivitatea
Sub buton8_Click()
Dim a As Integer, b As Integer, c As Integer
Do
a = InputBox("a = ", y)
b = InputBox("b = ", y)
a1 = a
b1 = b
Loop Until a > 0 And b > 0 And a > b
c = euclid(a, b)
If c = 1 Then
MsgBox " nr. sunt prime intre ele (" + Str$(a1) + "," + Str$(b1)
+ ")"
Else
MsgBox "Cmmdc (" + Str$(a1) + "," + Str$(b1) + ")=" + Str$
(euclid(a, b))
End If
End Sub
68. Funcţia euclid
Function euclid(a As Integer, b As Integer) As Integer
Dim r As Integer
Do
r = a Mod b
MsgBox r
131

130. a = b
b = r
Loop Until Not (r = 0 And r = 1)
If r = 1 Then
euclid = 1
Else
euclid = a
End If
End Function
69. CMMDC a două numere utilizând scăderi repetate
Private Sub Buton9_Click()
Dim a As Integer, b As Integer, c As Integer
Do
a = InputBox("a = ", y)
b = InputBox("b = ", y)
a1 = a
b1 = b
Loop Until a > 0 And b > 0 And a > b
c = euclid1(a, b)
If c = 1 Then
MsgBox " nr. sunt prime intre ele (" + Str$(a1) + "," + Str$(b1)
+ ")"
Else
MsgBox "Cmmdc (" + Str$(a1) + "," + Str$(b1) + ")=" + Str$
(euclid1(a, b))
End If
End Sub
70. Funcţia Euclid utilizând scăderi repetate
Function euclid1(a As Integer, b As Integer) As Integer
If a > b Then
euclid1 = euclid1(a - b, b)
Else
If a < b Then
euclid1 = euclid1(a, b - a)
Else
euclid1 = a
End If
End If
End Function
71. Funcţia Euclid utilizând scăderi repetate
Function euclid2(a As Integer, b As Integer) As Integer
If b = 0 Then
euclid2 = a
Else
euclid2 = euclid2(b, a Mod b)
End If
End Function
72. x ^ y utilizând un număr minim de înmulţiri
132

131. Sub Button15_Click()
Dim x As Integer, y As Integer, z As Integer, t As String, bb As
vector
Dim xx As Integer
Do
x = InputBox("a=", ib_title)
y = InputBox("b=", ib_title)
Loop Until (x > 0) And (y > 0) And (x >= y)
baza1 x, y, bb, xx
t = ""
MsgBox "n = " + Str$(xx)
For z = xx To 1 Step -1
t = t + Str$(bb.v(z))
Next
MsgBox t
End Sub
73. Verifică dacă un număr natural este palindrome sau nu
Sub Button16_Click()
Dim n As Long, m As Long
Do
n = InputBox("n=", ib_title)
Loop Until (n > 0)
m = n
If palindrom(n) = True Then
MsgBox "n=" + Str$(m) + " este plaindrom"
Else
MsgBox "n=" + Str$(m) + " nu este plaindrom"
End If
End Sub
74. Baza la exponent
Sub Button17_Click()
Dim x As Double, y As Byte, z As Double, t As Byte
Do
x = InputBox("baza=", ib_title)
y = InputBox("exponent=", ib_title)
Loop Until (x > 0) And (y > 0)
z = putere(x, y, t)
MsgBox Str$(z) + " " + Str$(t - 1)
End Sub
75. Quicksort
Sub Button18_Click()
Dim n As Integer, a As vector
cit_n "n = ", n
cit_date "a", n, a
'MsgBox "Sirul a este"
tipar "Sirul a este", n, a
divimp 1, n, a
'MsgBox "Sirul a sortat este"
tipar "Sirul a sortat este", n, a
End Sub
133

132. 76. Minimul dintr-un şir de numere utilizând divide et impera
Sub Button19_Click()
Dim n As Integer, a As vector
cit_n "n=", n
cit_date "a", n, a
'MsgBox "Sirul a este"
tipar "sirul dat este ", n, a
MsgBox "minimul in Sirul a este" + Str$(minim(1, n))
End Sub
77. Turnurile din Hanoi
Sub Button20_Click()
Dim n As Integer, a As sir, b As sir, c As sir
d = ""
a.s = "A"
b.s = "B"
c.s = "C"
n = InputBox("n=", ib_title)
hanoi n, a, b, c
MsgBox d
End Sub
78. Subrutina Hanoi
Sub hanoi(n As Integer, a As sir, b As sir, c As sir)
If n = 1 Then
d = d + "(" + a.s + "->" + b.s + "),"
Else
hanoi n - 1, a, c, b
d = d + "(" + a.s + "->" + b.s + "),"
hanoi n - 1, c, b, a
End If
End Sub
79. Subrutina back pentru permutări
Sub back_perm()
Dim k As Integer
k = 1
init k, st
While k > 0
Do
succesor am_suc, st, k
If am_suc = True Then
valid1 ev, st, k
End If
Loop Until (Not am_suc) Or (am_suc And ev)
If am_suc Then
If solutie(k) Then
tipar_r
Else
k = k + 1
init k, st
End If
Else
134

133. k = k - 1
End If
Wend
End Sub
80. Calculul sumei 1-1,1-1-1,………….,1-1-1-1-1-1-1…….-1
Private Sub Buttton3_Click()
Dim n As Integer, ss As String
cit_n "n = ", n
ss = ""
i = 0
j = 1
While (i < n)
ss = ss + " 1"
i = i + 1
k = 1
While k <= j And i < n
ss = ss + " -1"
i = i + 1
k = k + 1
Wend
j = j + 1
Wend
MsgBox ss
End Sub
135

134. Bibliografie
[1.] Brassard, G., Bratley, P. “Algorithmics - Theory and Practice”, Prentice-Hall, Englewood Cliffs,
1988.
[2.] Cormen, T.H., Leiserson, C.E., Rivest, R.L. “Introduction to Algorithms”, The MIT Press,
Cambridge, Masshusetts, 1992 (eighth printing).
[3.] Ellis, M., Stroustrup, B. “The Annotated C++ Reference Manual”, Addison-Wesley, Reading,
1991.
[4.] Graham, R.L., Knuth, D.E., Patashnik, O. “Concrete Mathematics”, Addison-Wesley, Reading,
1989.
[5.] Horowitz, E., Sahni, S. “Fundamentals of Computer Algorithms”, Computer Science Press,
Rockville, 1978.
[6.] Knuth, D.E. “Tratat de programarea calculatoarelor. Algoritmi fundamentali”, Editura Tehnica,
Bucuresti, 1974.
[7.] Knuth, D.E. “Tratat de programarea calculatoarelor. Sortare si cautare”, Editura Tehnica,
Bucuresti, 1976.
[8.] Lippman, S. B. “C++ Primer”, Addison-Wesley, Reading, 1989.
[9.] Livovschi, L., Georgescu, H. “Sinteza si analiza algoritmilor”, Editura Stiintifica si Enciclopedica,
Bucuresti, 1986.
[10.] Morariu N, Limbaje de programare, curs ID,2003
[11.] Sedgewick, R. “Algorithms”, Addison-Wesley, Reading, 1988.
[12.] Sedgewick, R. “Algorithms in C”, Addison-Wesley, Reading, 1990.
[13.] Sethi, R. “Programming Languages. Concepts and Constructs”, Addison-Wesley, Reading, 1989.
[14.] Smith, J.H. “Design and Analysis of Algorithms”, PWS-KENT Publishing Company, Boston, 1989.
[15.] Standish, T.A. “Data Structure Techniques”, Addison-Wesley, Reading, 1979.
[16.] Stroustrup, B. “The C++ Programming Language”, Addison-Wesley, Reading, 1991.
[17.] Stroustrup, B. “The Design and Evolution of C++”, Addison-Wesley, Reading, 1994.
[18.] http://thor.info.uaic.ro/~dlucanu/
136