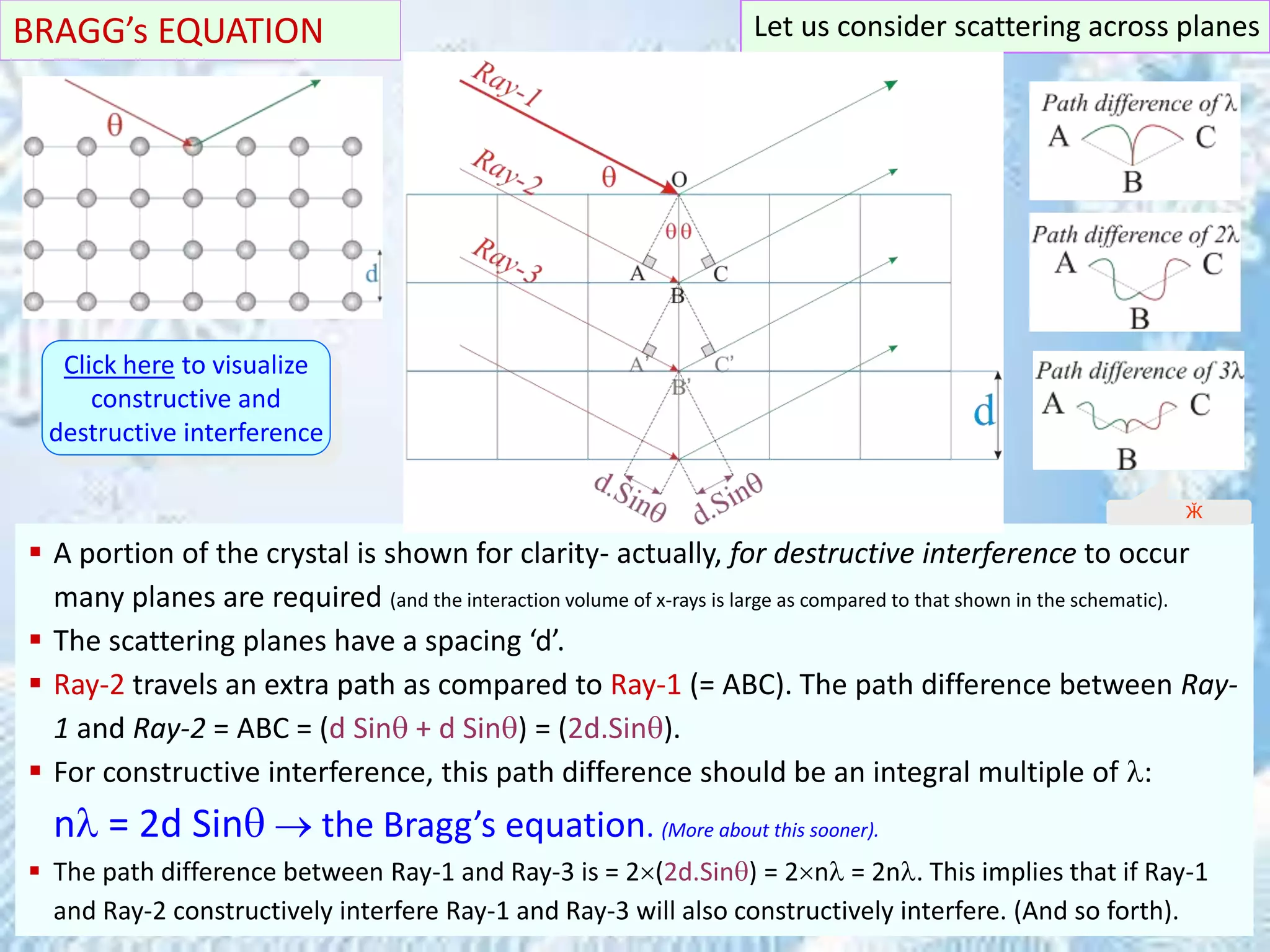
This document provides information on the Bragg's law of X-ray diffraction. It begins with an introduction to X-ray sources and generation, including how X-rays are produced by bombarding a target with electrons. It then explains Bragg's law of diffraction, which relates the scattering angle, wavelength of radiation, and interplanar spacing. The rest of the document discusses crystal structure determination using X-ray diffraction, including diagrams demonstrating Bragg's law and the conditions for constructive interference. It also addresses common questions around visualizing diffraction and obtaining Angstrom-scale information.

1. cove theory of x ray
diffraction

2. Presented BY
NAME : ADITYA SHARMA
CLASS : BSC VI SEM (C.S)
COLLEGE : RAI SAHEB BHANWAR SINGH
COLLEGE NASRULLAGANJ
SUBMITTED TO : GYANRAO DHOTE SIR

4. cove theory of x ray
diffraction

5. cove theory of x ray diffraction
 X- Ray Sources
 Diffraction: Bragg’s Law
 Crystal Structure Determination
Elements of X-Ray Diffraction
B.D. Cullity & S.R. Stock
Prentice Hall, Upper Saddle River (2001)
Recommended websites:
 http://www.matter.org.uk/diffraction/
 http://www.ngsir.netfirms.com/englishhtm/Diffraction.htm
MATERIALS SCIENCE
&
ENGINEERING
Anandh Subramaniam & Kantesh Balani
Materials Science and Engineering (MSE)
Indian Institute of Technology, Kanpur- 208016
Email: anandh@iitk.ac.in, URL: home.iitk.ac.in/~anandh
AN INTRODUCTORY E-BOOK
Part of
http://home.iitk.ac.in/~anandh/E-book.htm
A Learner’s Guide

6. Beam of electrons Target
X-rays
An accelerating (or decelerating) charge radiates electromagnetic radiation
 X-rays can be generated by decelerating electrons.
 Hence, X-rays are generated by bombarding a target (say Cu) with an electron beam.
 The resultant spectrum of X-rays generated (i.e. X-rays versus Intensity plot) is shown in
the next slide. The pattern shows intense peaks on a ‘broad’ background.
 The intense peaks can be ‘thought of’ as monochromatic radiation and be used for X-ray
diffraction studies.
Generation of X-rays

7. Mo Target impacted by electrons accelerated by a 35 kV potential shows the emission
spectrum as in the figure below (schematic)
The high intensity nearly monochromatic K x-rays can be used as a radiation source for
X-ray diffraction (XRD) studies  a monochromator can be used to further decrease the
spread of wavelengths in the X-ray
Intensity
Wavelength ()
0.2 0.6 1.0 1.4
White
radiation
Characteristic radiation →
due to energy transitions
in the atom
K
K
Intense peak, nearly
monochromatic
X-ray sources with different  for
doing XRD studies
Target
Metal
 Of K
radiation (Å)
Mo 0.71
Cu 1.54
Co 1.79
Fe 1.94
Cr 2.29

8. Elements (KV)  Of K1
radiation
(Å)
 Of K2
radiation (Å)
 Of Kβ
radiation (Å)
Kβ-Filter
(mm)
Ag 25.52 0.55941 0.5638 0.49707 Pd
0.0461
Mo 20 0.7093 0.71359 0.63229 Zr
0.0678
Cu 8.98 1.540598 1.54439 1.39222 Ni
0.017
Ni 8.33 1.65791 1.66175 1.50014 Co
0.0158
Co 7.71 1.78897 1.79285 1.62079 Fe
0.0166
Fe 7.11 1.93604 1.93998 1.75661 Mn
0.0168
Cr 5.99 2.2897 2.29361 2.08487 V
0.169
C.Gordon Darwin, Grandson of C. Robert Darwin developed the dynamic theory of scattering of x-rays (a tough theory!) in 1912
X-ray sources with different  for doing XRD studies

9. Absorption (Heat)
Incident X-rays
SPECIMEN
Transmitted beam
Fluorescent X-rays
Electrons
Compton recoil Photoelectrons
Scattered X-rays
Coherent
From bound charges
X-rays can also be refracted (refractive index slightly less than 1) and reflected (at very small angles)
• When X-rays hit a specimen, the interaction can
result in various signals/emissions/effects.
• The coherently scattered X-rays are the ones
important from a XRD perspective.
Incoherent (Compton modified)
From loosely bound charges
Click here to know more

10. Sets Electron cloud into oscillation
Sets nucleus into oscillation
Small effect  neglected
 A beam of X-rays directed at a crystal interacts with the electrons of the atoms in the crystal.
 The electrons oscillate under the influence of the incoming X-Rays and become secondary sources
of EM radiation.
 The secondary radiation is in all directions.
 The waves emitted by the electrons have the same frequency as the incoming X-rays  coherent.
 The emission can undergo constructive or destructive interference.
XRD  the first step
Schematics
Incoming X-rays
Secondary
emission
Oscillating charge re-radiates  In phase with
the incoming x-rays

11. Extra path traveled by incoming waves  AY
A B
X Y
Atomic Planes
Extra path traveled by scattered waves  XB
These can be in phase if
 incident = scattered
A B
X Y
But this is still reinforced scattering
and NOT reflection
Let us consider in-plane scattering
There is more to this
Click here to know more and get
introduced to Laue equations describing
diffraction

12. BRAGG’s EQUATION
 A portion of the crystal is shown for clarity- actually, for destructive interference to occur
many planes are required (and the interaction volume of x-rays is large as compared to that shown in the schematic).
 The scattering planes have a spacing ‘d’.
 Ray-2 travels an extra path as compared to Ray-1 (= ABC). The path difference between Ray-
1 and Ray-2 = ABC = (d Sin + d Sin) = (2d.Sin).
 For constructive interference, this path difference should be an integral multiple of :
n = 2d Sin  the Bragg’s equation. (More about this sooner).
 The path difference between Ray-1 and Ray-3 is = 2(2d.Sin) = 2n = 2n. This implies that if Ray-1
and Ray-2 constructively interfere Ray-1 and Ray-3 will also constructively interfere. (And so forth).
Let us consider scattering across planes
Click here to visualize
constructive and
destructive interference
See Note Ӂ later

13.  For Cu K radiation ( = 1.54 Å) and d110= 2.22 Å
n Sin = n/2d 
1 0.34 20.7º • First order reflection from (110)  110
2 0.69 43.92º
• Second order reflection from (110) planes  110
• Also considered as first order reflection from (220) planes  220
2 2 2
Cubic crystal
hkl
a
d
h k l

 
8
220
a
d 
2
110
a
d 
2
1
110
220

d
d
Relation between dnh nk nl and dhkl
e.g.
2 2 2
( ) ( ) ( )
nhnk nl
a
d
nh nk nl

 
2 2 2
hkl
nhnk nl
da
d
nn h k l
 
 
Order of the reflection (n)

14. 2 sinhkl hkln d 
In XRD nth order reflection from (h k l) is considered as 1st order reflection from (nh nk nl)
 sin2
n
dhkl

n n n n n n2 sinh k l h k ld 
1nhnk nl
hkl
d
d n

300
100
1
3
d
d

200
100
1
2
d
d

Hence, (100) planes are a subset of (200) planes
Important point to note:
In a simple cubic crystal, 100, 200, 300… are all allowed ‘reflections’. But, there are no atoms in the
planes lying within the unit cell! Though, first order reflection from 200 planes is equivalent
(mathematically) to the second order reflection from 100 planes; for visualization purposes of
scattering, this is better thought of as the later process (i.e. second order reflection from (100)
planes).
Note:
Technically, in Miller indices we factor out the common factors. Hence, (220)  2(110)  (110).
In XRD we extend the usual concept of Miller indices to include planes, which do not pass through
lattice points (e.g. every alternate plane belonging to the (002) set does not pass through lattice
points) and we allow the common factors to remain in the indices.
All these form the (200) set

15. I have seen diagrams like in Fig.1 where rays seem to be scattered from nothing!
What does this mean?Funda Check
 Few points are to be noted in this context. The ray ‘picture’ is only valid in the realm of geometrical
optics, where the wave nature of light is not considered (& also the discrete nature of matter is
ignored; i.e. matter is treated like a continuum). In diffraction we are in the domain of physical optics.
 The wave impinges on the entire volume of material including the plane of atoms (the effect of which
can be quantified using the atomic scattering power* and the density of atoms in the plane). Due to
the ‘incoming’ wave the atomic dipoles are set into oscillation, which further act like emitter of waves
 In Bragg’s viewpoint, the atomic planes are to be kept in focus and the wave (not just a ray) impinges
on the entire plane (some planes have atoms in contact and most have atoms, which are not in
contact along the plane  see Fig.2).
* To be considered later
A plane in Bragg’s viewpoint can be characterized by two factors: (a) atomic density (atoms/unit area on the plane), (b) atomic scattering
factor of the atoms.
Fig.1
Fig.2Wave impinging on a crystal (parallel wave-front)
(note there are no ‘rays’)
??

16. How is it that we are able to get information about lattice parameters of the
order of Angstroms (atoms which are so closely spaced) using XRD?
Funda Check
 Diffraction is a process in which
‘linear information’ (the d-spacing of the planes)
is converted to ‘angular information’ (the angle of diffraction, Bragg).
 If the detector is placed ‘far away’ from the sample (i.e. ‘R’ in the figure below is large) the
distances along the arc of a circle (the detection circle) get amplified and hence we can make
‘easy’ measurements.
 This also implies that in XRD we are concerned with angular resolution instead of linear
resolution.
Later we will see that in powder
diffraction this angle of deviation
(2) is plotted instead of .

17. Forward and Back Diffraction
Here a guide for quick visualization of forward and backward scattering (diffraction) is presented

18.  We had mentioned that Bragg’s equation is a negative statement: i.e. just because
Bragg’s equation is satisfied a ‘reflection’ may not be observed.
 Let us consider the case of Cu K radiation ( = 1.54 Å) being diffracted from (100) planes
of Mo (BCC, a = 3.15 Å = d100).
The missing ‘reflections’
100 1002d Sin  100
100
1.54
0.244
2 2(3.15)
Sin
d

    100 14.149  
But this reflection is absent in BCC Mo
The missing reflection is due to the presence of additional atoms in the unit cell
(which are positions at lattice points)  which we shall consider next
The wave scattered from the middle plane is out of
phase with the ones scattered from top and bottom
planes. I.e. if the green rays are in phase (path difference
of ) then the red ray will be exactly out of phase with
the green rays (path difference of /2).

19. How to visualize the occurrence of peaks at various angles
It is ‘somewhat difficult’ to actually visualize a random assembly of crystallites giving peaks at various angels in a XRD scan.
The figures below are expected to give a ‘visual feel’ for the same. [Hypothetical crystal with a = 4Å is assumed with
=1.54Å. Only planes of the type xx0 (like (100,110)are considered].
Random assemblage of
crystallites in a material
As the scan takes place at increasing
angles, planes with suitable ‘d’,
which diffract are ‘picked out’ from
favourably oriented crystallites
h2 hkl d Sin() 
1 100 4.00 0.19 11.10
2 110 2.83 0.27 15.80
3 111 2.31 0.33 19.48
4 200 2.00 0.39 22.64
5 210 1.79 0.43 25.50
6 211 1.63 0.47 28.13
8 220 1.41 0.54 32.99
9 300 1.33 0.58 35.27
10 310 1.26 0.61 37.50
For convenience the source
may be stationary (and the
sample and detector may
rotate– but the effect is
equivalent)

20. Diffuse peak from
Cu-Zr-Ni-Al-Si
Metallic glass
(XRD patterns) courtesy: Dr. Kallol Mondal, MSE, IITK
Actual diffraction
pattern from an
amorphous solid
 A amorphous solid which shows glass transition in a Differential Scanning Calorimetry (DSC)
plot is also called a glass. In ‘general usage’ a glass may be considered equivalent to a
amorphous solid (at least loosely in the structural sense).
 Sharp peaks are missing. Broad diffuse peak survives
→ the peak corresponds to the average spacing between atoms which the diffraction experiment ‘picks
out’
Amorphous solid