WSDM 2018 Tutorial on Influence Maximization in Online Social Networks

Influence Maximization in
Online Social Networks
Cigdem Aslay, Laks V.S. Lakshmanan, Wei Lu,
and Xiaokui Xiao
WSDM 2018 Tutorial

What’s new?
• Previous tutorials on influence
maximization
• Several real life applications
• Recent advances in scalable algorithms
• Learning the Models or even Influence
Functions – offline/online
• (The rich) Life beyond classical IM

Disclaimers
• No claim of completeness.
• Bird’s eye tour of what we do cover.
• If you don’t see or hear about your
research, …

Overview of Tutorial
• Part I: Introduction
• Part II: Scalable Approximation Algorithms and
Extensions to Topic, Time, and Location
• Part III:
(a) Multiple Campaigns
(b) Social Advertising
• Part IV:
(a) Offline Learning of Models
(b) Online Learning of Models
(c) Summary and Open Challenges

• Information Propagation in Networks
• Real Life Applications of Influence Analysis
• Information Propagation Models
• Definition of Influence Maximization and
Variants
• Some Theory: hardness, approximation,
baselines.
• Heuristics.
Overview of Part I: Introduction

Overview of Part I: Introduction
• Information Propagation in Networks
• Real Life Applications of Influence Analysis
• Information Propagation Models
• Definition of Influence Maximization and
Variants
• Some Theory: hardness, approximation,
baselines.
• Heuristics.

Online Social Networking Sites

Information Propagation
People are connected and perform actions
nice read
indeed!
09:3009:00
comment, link,
rate, like,
retweet, post a
message, photo,
or video, etc.
friends,
fans,
followers,
etc.

Real-life Applications of Influence
Analysis
• Viral Marketing
• adoption of prescription drugs
• regulatory mechanism for yeast cell cycle
• voter turnout influence in 2010 US
congressional elections
• influence maximization for social good
(HEALER)

Social Influence
Viral Marketing
Social media analytics
Spread of falsehood and rumors
Interest, trust, referrals
Adoption of innovations
Human and animal epidemics
Expert finding
Behavioral targeting
Feed ranking
“Friends” recommendation
Social search
!12

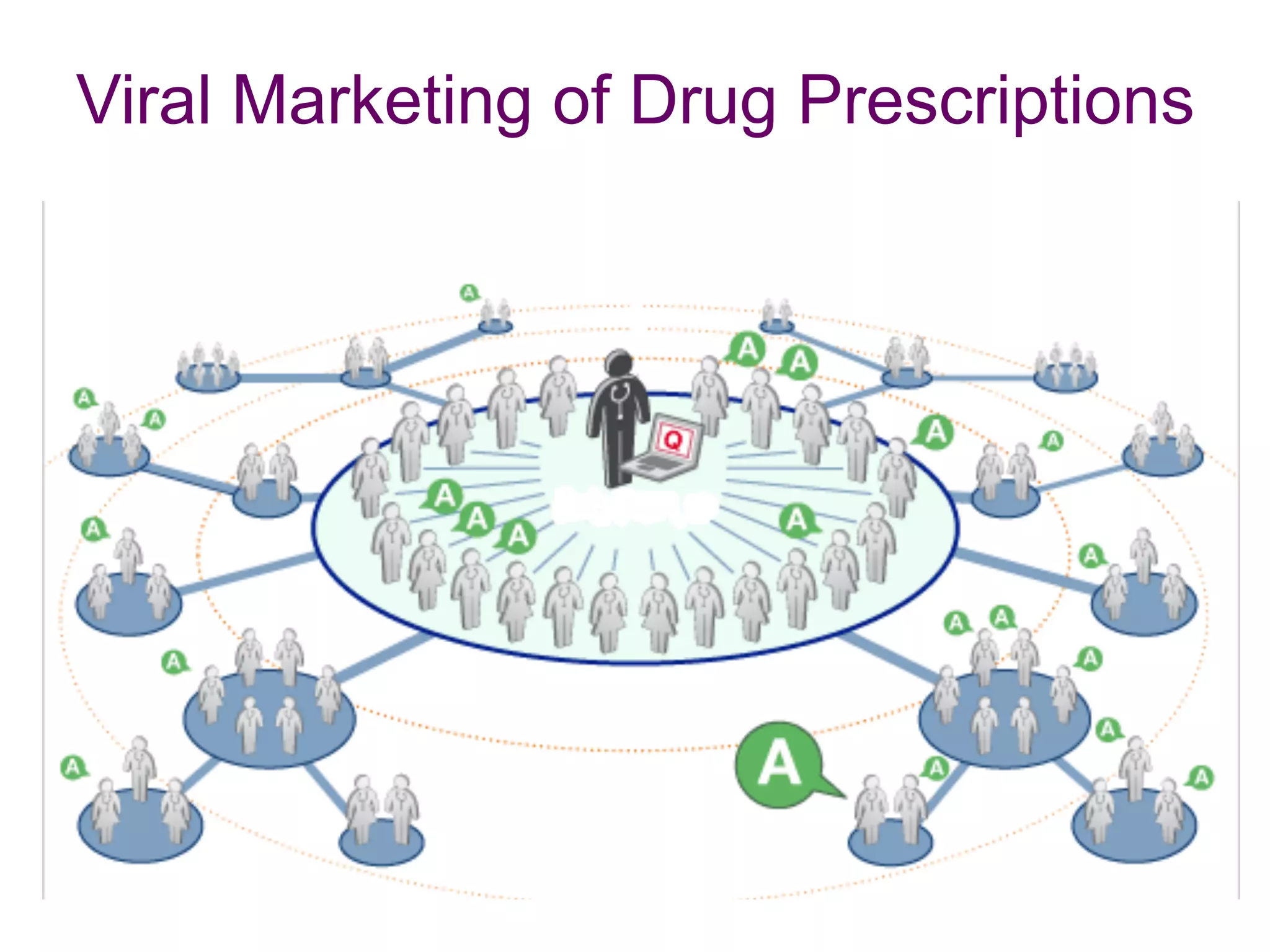
Viral Marketing of Drug Prescriptions

Propagation Drug Prescriptions
• nodes = physicians; links = ties.
• Question: does contagion work through the network?
• answer: affirmative.
• volume of usage (prescription of drug) controls contagion
more than whether peer prescribed drug.
• genuine social contagion found to be at play, even after
controlling for mass media marketing efforts, and global
network wide changes.
• targeting sociometric opinion leaders definitely beneficial.
[R. Iyengar, et al. Opinion Leadership and Social Contagion in New Product  
Diffusion. Marketing Science, 30(2):195–212, 2011.]

Analysis workflow for Saccharomyces cerevisiae.
IM and Yeast Cell Cycle Regulation
[Gibbs DL, Schmulevich I (2017). Solving the influence maximization problem reveals regulatory
organization of the yeast cell cycle. PLOS Compt.Biol 13(6). e1005591. https://doi.org/10.1371/journal.pcbi.
1005591].

Topology of influential nodes.
[Gibbs DL, Shmulevich I (2017) Solving the influence maximization problem reveals regulatory organization of the yeast cell cycle.
PLOS Computational Biology 13(6): e1005591. https://doi.org/10.1371/journal.pcbi.1005591]
http://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1005591
IM and Yeast Cell Cycle Regulation

Yeast Cell Cycle Study Conclusions
• IM contributes to understanding of yeast cell
cycles.
• Can we find minimum sets of biological
entities that have the greatest influence in the
network context?
• they in turn have greatest control/influence
on network ➔ understand link between
network dynamics and disease.

Social Influence in Political Mobilization
• is influence in OSN real or as effective as
offline SN?
• what about weak ties?
• can OSN be used to harness behavioral
change at scale?
• A large scale (61M users) study on
Facebook.
[RM. Bond et al. A 61-million … poitical mobilization. Nature 489, 295-298
(2012) doi:10.1038/nature11421].

A 61 Million User Experiment
• users split into a (randomized) control group,
informational message group, and social group.
• Info. msg group (611 K) shown msg encouraging
voting, clicking on “I voted”. Count of fb users who
had reported voting.
• Social group (60 M) also shown faces/profiles of
select subset of friends who had voted.
• Control group (613 K) no message.

A 61 Million User Experiment
[RM Bond et al. Nature 489, 295-298 (2012) doi:10.1038/nature11421].

Effect of friend’s mobilization treatment on a user’s behavior 
[RM Bond et al. Nature 489, 295-298 (2012) doi:10.1038/nature11421].

Social Influence in Political Mobilization
(Conclusions)
• Online mobilization works ➔ improved
turnout.
• social mobilization far more effective than
informational mobilization.
– close friends exerted 4x more influence
than the message alone.
– propagation made a real difference.
– close friends far more effective than
(arbitrary) fb friends.

IM for Social Good – The Healer

IM for Social Good – The Healer
homeless  
youth
Facebook
application
homeless  
youth
. 
. 
.
DIME
solver
shelter  
official
action
recommendation
feedback
[Amulya Yadav et al. Using Social Networks to Aid Homeless Shelters: Dynamic Influence Maximization Under
Uncertainty. Proc. Int. Conf. on Autonomous Agents and Multiagent Systems (AAMAS), 2016.]
HEALER PROJECT: http://teamcore.usc.edu/people/amulya/healer/index.html

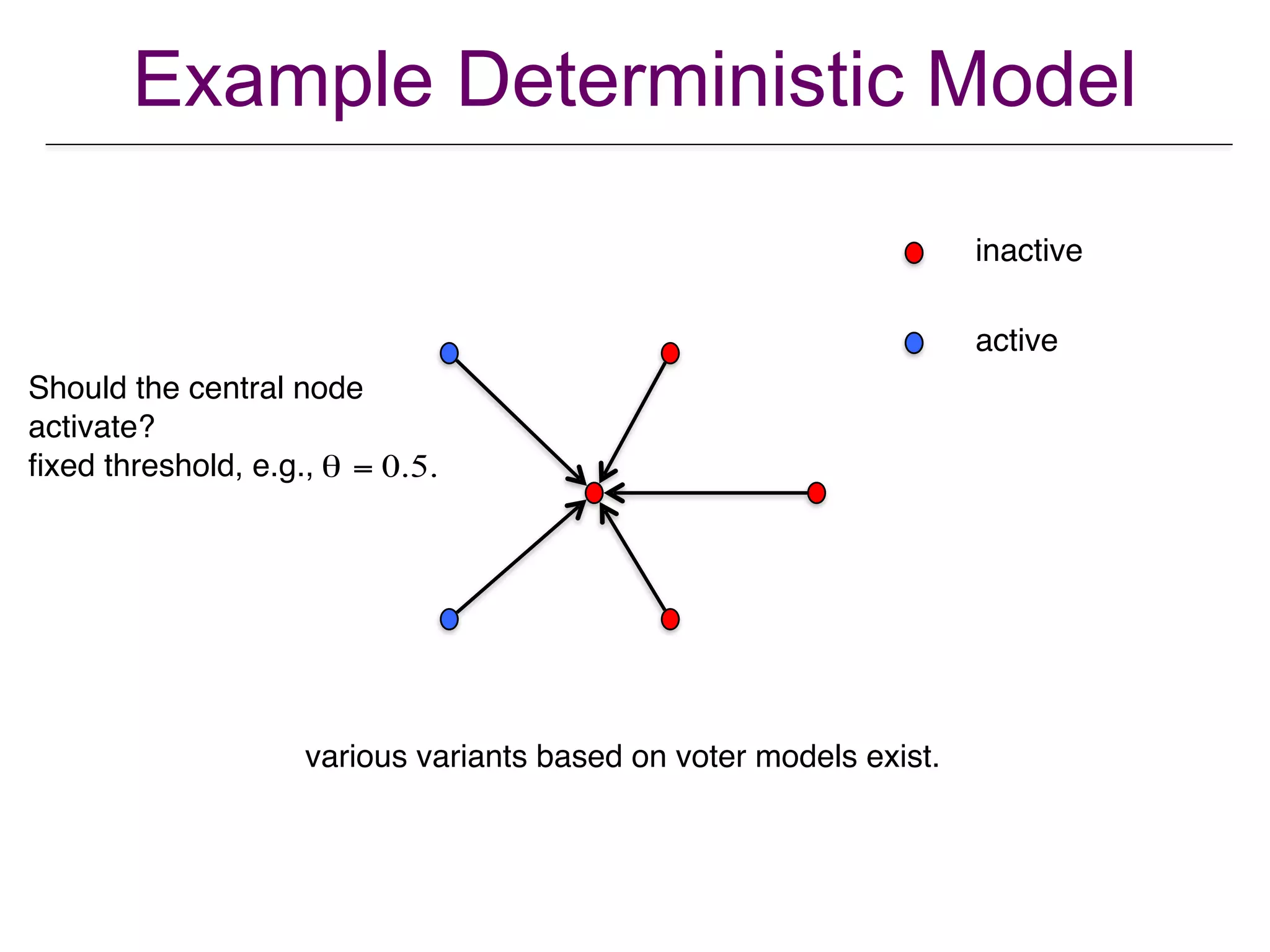
Propagation/Diffusion Models
• How does influence/information travel?
• Deterministic versus stochastic models.
• Discrete time versus continuous time models.
• Phenomena captured: infection or product
adoption?
[W. Chen, L., and Carlos Castillo. Information and Influence Propagation in Socia
Networks. Morgan-Claypool 2013].

Some basic terminology
• will use metaphors from marketing (e.g., adopt a
product/technology/idea), from epidemiology (e.g.,
get infected).
• in the intro., mostly focus on single (product/infection/
rumor) campaign.
• multiple campaigns in Parts III and IV.
active inactive
Progressive Models.

Example Deterministic Model
inactive
active
Should the central node
activate?
fixed threshold, e.g., θ = 0.5.
various variants based on voter models exist.

Stochastic Models
• network = probabilistic graph. assumed fixed.
• Discrete time: time = natural numbers; proceeds in discrete
steps.
• Continuous time: time increases continuously.
• Discrete time stochastic models:
– two simple yet expressive and elegant models.
• independent cascade (IC).
• linear threshold (LT).
• generalizations exist.
• Continuous time stochastic models:

Independent cascade model
0.3
0.1
0.1
0.02
0.2
0.1
0.2
0.4
0.3
0.1
0.3
0.3
0.30.04
0.2
0.1
0.7
0.1
0.01
0.05
[Kempe et al. KDD 2003].
• Each edge has
influence probability .
• Seeds selected activate at
time
• At each , each active
node gets one shot at
activating its inactive
neighbor ; succeeds w.p.
and fails w.p.
• Once active, stay active.
(u,v)
puv
t = 0.
t > 0
u
v
puv (1− puv ).
similar to infection propagation.

0.3
0.1
0.1
0.2
0.2
0.3
0.2
0.4
0.3
0.1
0.3
0.3
0.30.2
0.2
0.5
0.5
0.8
0.1
0.2
0.3
0.7
0.3
0.5
0.6
0.3
0.2
0.4
0.8
Linear threshold model
[Kempe et al. KDD 2003].
• Each edge has weight
• Each node chooses a
threshold at random.
• Activate if total
influence of active
in-neighbors exceeds
node’s threshold.
(u,v)
w(u,v): w(u,v) ≤1
u
∑
similar to technology adoption or opinion propagation.

For all discrete time models
• Let be a set of nodes activated at time 0.
– initial adaptors, “patients zero”, …
• denotes the expected number of nodes
activated under model M when diffusion
saturates.
• Key IM problem: choose S to maximize
• Model parameters: edge weights/probabilities.
• Problem parameters: budget k.

Continuous Time
• = conditional prob. 
that gets the infection transmitted  
from at time given that was  
infected at time .
• = transmission rate
• assumed to be shift invariant:
– e.g.,
[Gomez-Rodriguez and Schölkopf. IM in continuous time diffusion networks.
ICML 2012].

What to optimize?
• := #nodes infected within horizon  
given seed nodes
•
• Key problem: Choose S to maximize
• Model parameters: rate parameters
(edges).
• Problem parameters: horizon T and budget k.

Influence Maximization Defined
• Core optimization problem in IM: Given a
diffusion model M, a network G = (V,E),
model parameters, and problem parameters
(budget, time horizon [for continuous time
models only]). Find a seed set under
budget that maximizes or
(expected) spread.

Variants
• There may be a cost to seeding a node; seeding cost may not be
uniform.
• Benefit of activating different nodes may not be uniform.
• Priorities of influencing different communities may be different.
• More than one product/idea/phenomenon may be at play:
– competition
– complementation
• Social advertising
• Minimize seed cost to achieve given target
• Minimize (diffusion) time to achieve given target
• Others …

Complexity of IM
• Theorem: The IM problem is NP-hard for
several major diffusion models under both
discrete time and continuous time.
– IC model: reduction from max-k cover.
– LT model: vertex cover.
– continuous time ! generalizes IC model.

Complexity of Spread Computation
• Theorem: It is #P-hard to compute the
expected spread of a node set under both IC
and LT models.
– IC model: reduction from s!t connectivity
in uncertain networks.
– LT model: reduction from counting #simple
paths in a digraph.

Properties of Spread Function
(resp., ) is  
monotone: and
submodular:
marginal gain.

Approximation of Submodular Function
Optimization
• Theorem: Let be a monotone
submodular function, with Let
and resp. be the greedy and optimal solutions.
Then
• Theorem: The spread function is monotone
and submodular under various major diffusion
models, for both discrete and continuous time.
[Nemhauser et al. An analysis of the approximations for maximizing submodular
set functions. Math. Prog., 14:265–294, 1978.]

Submodularity of Spread
• Key notion: live edge model.
– IC: LE model = possible world obtained from
sampling edges, w.p. = edge probability.
– LT: LE model = possible world obtained by
having each node choose in-neighbor, w.p.  
edge weight.
– spread = weighted sum of reachability, which
is monotone and submodular.

Baseline Approximation Algorithm
Monte Carlo simulation for estimating  
expected spread.
CELF leverages submodularity to save on  
unnecessary evals of marginal gain.
Greedy still extremely slow on large networks.
[Leskovec et al. Cost-effective outbreak detection in networks. KDD 2007]

Heuristics
• Numerous heuristics have been proposed.
• We will discuss PMIA (IC), SimPath (LT) [if
time permits], and PMC$ (IC).  
 
 
 
$Technically PMC is an approximation
algorithm; however, to make it scale requires
setting small parameter values which can
compromise accuracy.

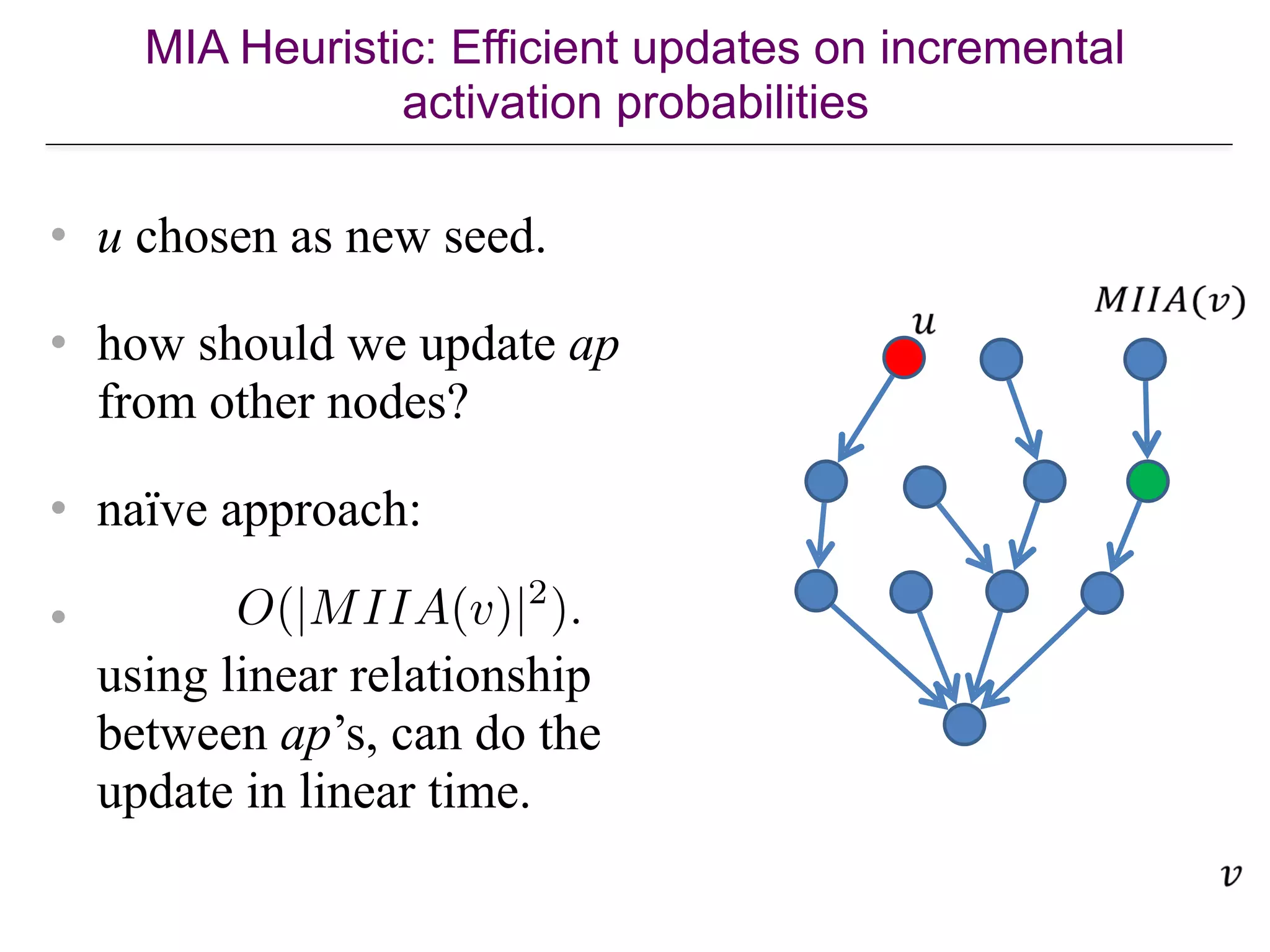
Maximum Influence Arborescence
(MIA) Heuristic
0.3
0.1
0.1
0.02
0.2
0.1
0.2
0.4
0.3
0.1
0.3
0.3
0.3
0.04
0.2
0.1
0.7
0.1
0.01
0.05

• For given node v, for each
node u, compute the max.
influence path from u to v.
• drop paths with influence <
0.05.
• max. influence in-
arborescence (MIIA) = all
MIPs to v; can be computed
efficiently.
• influence to v computed over
its MIIA.
[Chen et al. Efficient influence maximization in social networks KDD, pp. 199–208, 2009]

MIA Heuristic: Computing Influence
through the MIA structure
• Recursive computation of activation probability
ap(u) in its in-arborescence.
• {in-neighbors of u in MIIA of u}.

MIA Heuristic: Efficient updates on incremental
activation probabilities

• u chosen as new seed.
• how should we update ap
from other nodes?
• naïve approach:
•  
using linear relationship
between ap’s, can do the
update in linear time.

The SimPath Algorithm
In lazy forward manner, in each iteration,
add to the seed set, the node providing
the maximum marginal gain in spread.
Simpath-Spread
Vertex Cover
Optimization
Look ahead
optimization
Improves the efficiency
in the first iteration
Improves the efficiency
in the subsequent iterations
Compute marginal gain by
enumerating simple paths
[Goyal, Lu, & L. Simpath: An Efficient Algorithm for Influence Maximization under the
Linear Threshold Model.ICDM 2011]

Other Heuristics (up to 2013)
• see [W. Chen, L., and Carlos Castillo. Information and Influence Propagation
in Socia Networks. Morgan-Claypool 2013].

PMC
• Follows classical approach:
– greedy seed selection based on max marginal
gain;
– MC simulations for estimating marginal gain.
• Recall traditional approach:
– traditional approach: in each round, use R MC
simulations ! R possible worlds;
– compute gain of nodes in each PW and take
average.
[Ohsaka et al. Fast… IM …with Pruned Monte-Carlo Simulations AAAI 2014].

PMC
• Key insight of PMC approach:
– pre-provision R possible worlds;
– in each greedy round, compute gain of nodes
using the same R possible worlds.
• additional optimizations:
– use strongly connected components to save on
traversal time.
– prune BFS when possible: e.g., if v->>h, then
nodes reachable from h are reachable from v.
• pick h to be a max degree “hub”
– if no node reachable from v is reachable from a
seed just added, no need to revise v’s MG.

PMC
• PMC preserves approx. guarantee, in principle.
However, in experiments, the authors arbitrarily
set R=200.
– variance can be high.
• experiments show PMC dominates previous
heuristics including PMIA, IRIE, …
• unlike traditional MC approach, need to store
possible worlds – memory overhead.
• Larger R ! higher accuracy and higher memory
overhead.

Part I Summary
• Significance of influence and real-life
applications of influence analysis.
• basic diffusion models.
• definition of influence maximization problem
and variants.
• underlying theory: hardness, approximation.
• heuristics.

Part II Outline
!57
• Algorithms with Worst-Case Guarantees
– Sketch-based algorithm
– Reverse influence sampling
• Context-Aware Influence Maximization
– Time-aware
– Location-aware
– Topic-aware

Sketch-based Algorithms
!58
•
[Cohen et al., “Sketch-based Influence Maximization and Computation: Scaling up with Guarantees”, CIKM 2014]
0.4
0.3
0.60.5
0.2
0.3 0.4
…

!59
•
0.4
0.3
0.60.5
0.2
0.3 0.4
…

!60
•
0.4
0.3
0.60.5
0.2
0.3 0.4
…

!61
•
0.4
0.3
0.60.5
0.2
0.3 0.4
…

Reachability Sketches
!62
•
0.3
0.4
0.5
0.1
0.7

!63
•
0.3
0.4
0.5
0.1
0.7
0.3
0.3
0.5
0.1
0.1

!64
•
0.3
0.4
0.5
0.1
0.7
0.3
0.3
0.5
0.1
0.1

!65
• Problem:
– Influence estimation based on one
rank would be inaccurate
0.3
0.4
0.5
0.1
0.7
0.3
0.3
0.5
0.1
0.1

!66
•
0.3
0.4
0.5
0.1
0.7
0.3
0.3
0.5
0.1
0.1

!67
•
0.3
0.4
0.5
0.1
0.7
0.3, 0.5
0.3, 0.4
0.5
0.1
0.1, 0.3

!68
•
0.3
0.4
0.5
0.1
0.7
0.3, 0.5
0.3, 0.4
0.5
0.1
0.1, 0.3

Sketch-based Greedy
!69
• 0.1, 0.2, 0.5
0.2, 0.2, 0.4
0.5, 0.7, 0.8
0.5, 0.7, 0.8
0.1, 0.3, 0.6

Sketch-based Greedy
!70
• 0.1, 0.2, 0.5
0.2, 0.2, 0.4
0.5, 0.7, 0.8
0.5, 0.7, 0.8
0.1, 0.3, 0.6


!71
• Summary
– Advantages
• Expected time near-linear to the total size
of possible worlds
• Provides an approximation guarantee with
respect to the possible worlds considered
– Disadvantage
• Does not provide an approximation
guarantee on the “true” expected influence

Part II Outline
!72
– Time-aware
– Location-aware
– Topic-aware

Reverse Influence Sampling
!73
•

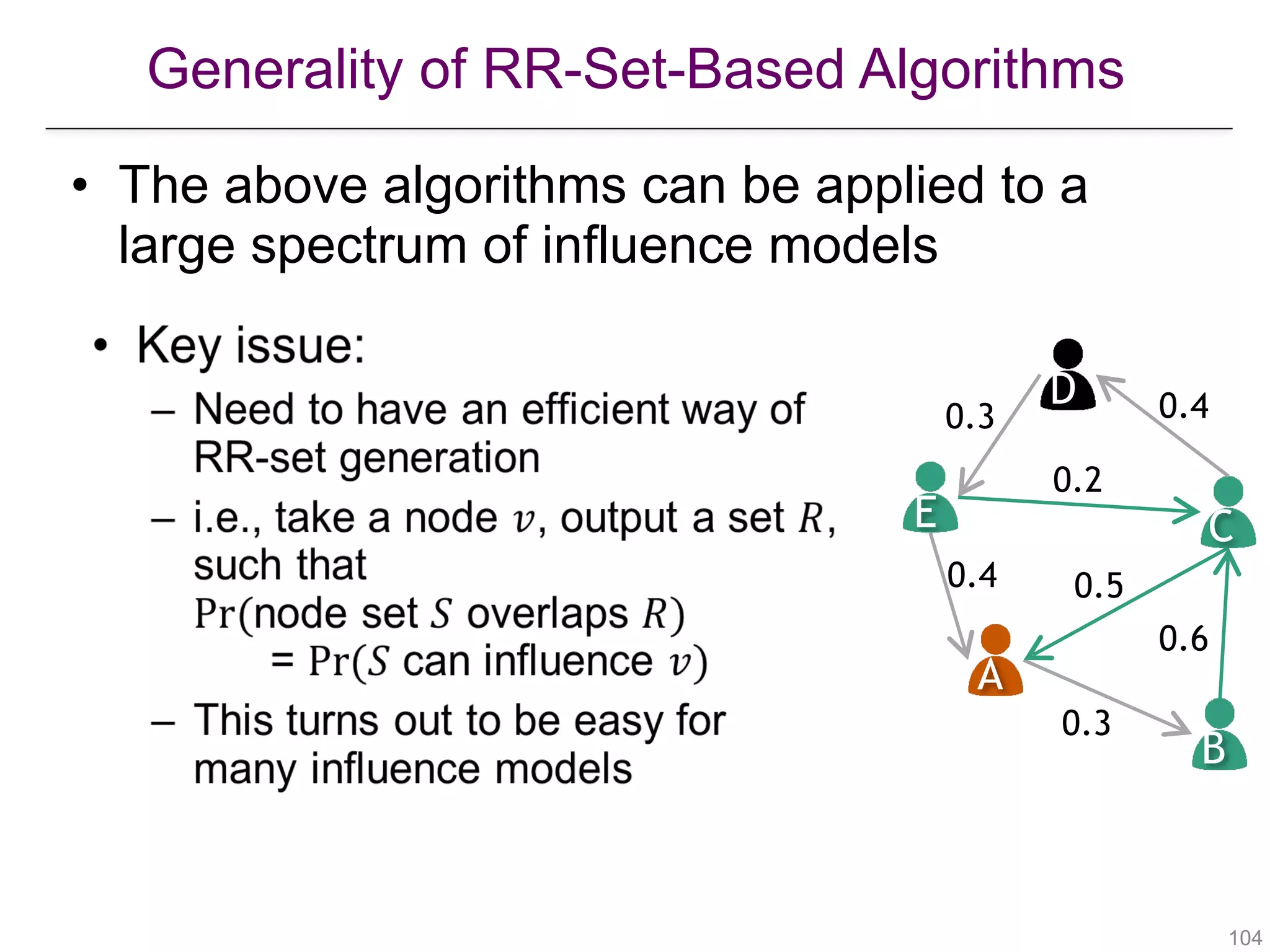
Reverse Reachable Sets (RR-Sets)
[Borgs et al., “Maximizing Social Influence in Nearly Optimal Time”, SODA 2014]
!74
•
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4

!75
•
start from a
random node
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4
RR-set = {A}

!76
•
start from a
random node
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4
sample its  
incoming edges
RR-set = {A}

!77
•
start from a
random node
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4
sample its  
incoming edges
RR-set = {A}
add the sampled
neighbors

!78
•
start from a
random node
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4
sample its  
incoming edges
RR-set = {A, C}
add the sampled
neighbors

!79
start from a
random node
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4
sample its/their  
incoming edges
RR-set = {A, C}
add the sampled
neighbors
•

!80
•
start from a
random node
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4
incoming edges
RR-set = {A, C}
add the sampled
neighbors

!81
•
start from a
random node
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4
incoming edges
RR-set = {A, C, B, E}
add the sampled
neighbors

!82
•
start from a
random node
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4
incoming edges
add the sampled
neighbors

!83
•
start from a
random node
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4
incoming edges
add the sampled
neighbors
• Intuition:
– The RR-set is a sample set of nodes that can
influence node A

Influence Estimation with RR-Sets
!84
•
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4

!85
•
R1 = {A, C, B}
R2 = {B, A, E}
R3 = {C}
R4 = {D, C}
R5 = {E}

!86
•
R1 = {A, C, B}
R2 = {B, A, E}
R3 = {C}
R4 = {D, C}
R5 = {E}

Borgs et al.’s Algorithm
!87
•
R1 = {A, C, B}
R2 = {B, A, E}
R3 = {C}
R4 = {D, C}
R5 = {E}

!88
•
R1 = {A, C, B}
R2 = {B, A, E}
R3 = {C}
R4 = {D, C}
R5 = {E}

!89
•
R1 = {A, C, B}
R2 = {B, A, E}
R3 = {C}
R4 = {D, C}
R5 = {E}

!90
•
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4

!91
•

!92
•

Two-Phase Influence Maximization
!93
• Key difference with Borgs et al.’s algorithm:
– Borgs et al. bounds the total cost of RR-set construction
– Two-phase bounds the number of RR-sets used
[Tang et al., “Influence Maximization: Near-Optimal Time Complexity Meets Practical Efficiency”, SIGMOD 2014]
Phase 1: Parameter
Estimation
Phase 2: Node
Selection
RR-sets
RR-sets results
“Please take 80k RR-sets.”

!94
•
[Tang et al., “Influence Maximization: Near-Optimal Time Complexity Meets Practical Efficiency”, SIGMOD 2014]

Two Lower Bounds of OPT
!95
•
[Tang et al., “Influence Maximization: Near-Optimal Time Complexity Meets Practical Efficiency”, SIGMOD 2014] 
[Tang et al., “Influence Maximization in Near-Linear Time: A Martingale Approach”, SIGMOD 2015]

Trial-and-Error Estimation of Lower Bound
!96

yes

no

!97
•

!98
•

!99
•

Stop-and-Stare Algorithms
[Nguyen et al., “Stop-and-Stare: Optimal Sampling Algorithms for Viral Marketing in Billion-scale Networks”,
SIGMOD 2016]
!101
•

Greedy

!102

yes

no
SIGMOD 2016]

!103
• Summary
– Advantage
• Better empirical efficiency than two-phase
– But no improvement in terms of time
complexity
• Note: The original paper contains a series
of bugs
– Pointed out in [Huang et al., VLDB 2017]
– Fixed in a technical report on Arxiv
SIGMOD 2016] 
[Huang et al., “Revisiting the Stop-and-Stare Algorithms for Influence Maximization, VLDB 2017]

Generality of RR-Set-Based Algorithms
!104
• The above algorithms can be applied to a
large spectrum of influence models
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4

Part II Outline
!105
– Time-aware
– Location-aware
– Topic-aware

Time-Aware Influence Maximization
[Chen et al., “Time-Critical Influence Maximization in Social Networks with Time-Delayed Diffusion Process”,  
AAAI 2012] 
[Liu et al., “Time Constrained Influence Maximization in Social Networks”, ICDM 2012] 
!106
• Motivation
– Marketing campaigns are often time-dependent
– Influencing a customer a week after a promotion
expires may not be useful

!107
• Motivation
– Marketing campaigns are often time-dependent
– Influencing a customer a week after a promotion
expires may not be useful
• Objective
– Take time into account in influence maximization
AAAI 2012] 
[Liu et al., “Time Constrained Influence Maximization in Social Networks”, ICDM 2012]

!108
•

AAAI 2012] 

!109
•

AAAI 2012] 

!110
•
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4

AAAI 2012] 

Location-Aware Influence Maximization
[Zhang et al., “Evaluating Geo-Social Influence in Location-Based Social Networks”, CIKM 2012] 
[Li et al., “Efficient Location-Aware Influence Maximization”, SIGMOD 2014]
!111
• Motivation
– Some marketing campaigns are location-dependent
• E.g., promoting an event in LA
– Influencing users far from LA would not be very useful
• Objective
– Maximize influence on people close to LA

!112
•

!113
• Algorithms
– Existing work uses heuristics
– It can also be solved using RR-sets
– RR-set generation:
• The starting node should be  
sampled based on the location  
scores
A
B
CE
D
0.4
0.3
0.6
0.5
0.2
0.3 0.4

Location- and Time-Aware Influence
Maximization
[Song et al., “Targeted Influence Maximization in Social Networks”, CIKM 2016]
!114
• Takes both location and time into account
– Location: each user has a location score
– Time: each edge has a time delay; influence has a
deadline T
• Algorithm: RR-sets
– The starting node is chosen based on the location
scores
– When an edge is sampled, its time delay is also sampled
– Omit nodes that cannot be reached before time T

Location- and Time-Aware Influence
Maximization
!115
• Takes both location and time into account
– Location: each user has a location score
– Time: each edge has a time delay; influence has a
deadline T
• Algorithm: RR-sets
– The starting node is chosen based on the location
scores
– When an edge is sampled, its time delay is also sampled
– Omit nodes that cannot be reached before time T
[Song et al., “Targeted Influence Maximization in Social Networks”, CIKM 2016]

Location-to-Location Influence Maximization
[Saleem et al., “Location Influence in Location-based Social Networks”, WSDM 2017]
!116
•
WS 
DM

Location-to-Location Influence Maximization
!117
•
[Saleem et al., “Location Influence in Location-based Social Networks”, WSDM 2017]

Part II Outline
!118
– Time-aware
– Location-aware
– Topic-aware

Topic-Aware Influence Maximization
[Chen et al., “Real-Time Topic-Aware Influence Maximization Using Preprocessing”, CSoNet 2015] 
[Aslay et al., “Online Topic-Aware Influence Maximization Queries”, EDBT 2014]
!119
• Motivation:
– Influence propagation is often topic dependent
– A doctor may have a large influence on health-
related topics, but less so on tech-related topics
• Objective:
– Incorporate topics into influence maximization
Red wine is good
for health.
Party time!
iPhone X is great! Ya right…

!120
•
health tech
0.7
0.1
health tech
0.5 0.5

!121
• Objective:
– Influence maximization given a topic distribution
• Algorithms:
– Offline processing can be done using RR-sets
– Existing work considers online processing:
• Pre-compute some information
• When given a topic distribution, quickly identify a good
seed set using the pre-computed information

!122
• Existing algorithms
– Offline phase:
• Select a few topic distributions
• Precompute the results of influence maximization for
each distribution
– Online phase:
• Given a query topic distribution, either
– Return the result for one of the precomputed distribution, or
– Take the results for several precomputed distributions, and do
rank aggregations

[Chen et al., “Online Topic-Aware Influence Maximization”, VLDB 2015]
!123
• An improved algorithm
– Offline phase:
• For each node, heuristically estimate its maximum
influence under any topic distribution
– Online phase:
• Maintain a priority queue of nodes
• Examine nodes in descending order of their estimated
maximum influence
• Additional heuristics to derive upper bounds of marginal
influence

!124
• Can we use pre-computed RR-sets
• No
• Reason:
– Generation of RR-sets require knowing the probability of
each edge
– The probabilities cannot be decided since the topic
distribution is not given
• [VLDB 2015]: changes the problem definition and
allows RR-sets pre-computation
[Li et al., “Real-time targeted influence maximization for online advertisements”, VLDB 2015]

Node-Topic-Aware Influence Maximization
!125
•
health tech
0.7
0.1
health tech
0.5 0.5
0.5

Node-Topic-Aware Influence Maximization
!126
• Algorithm:
– Offline phase: for each topic, pre-compute RR-sets
• Sample starting node according to the topic weight
– Online phase: given a topic distribution, take a
number of RR-sets from each topic involved, then
run Greedy
• Example: (health: 0.5, tech: 0.1)
• Take samples for health and tech at a ratio of 5:1

Part II Outline
!127
– Time-aware
– Location-aware
– Topic-aware

Motivations
• What we’ve seen so far
– Single-entity models (IC, LT, …)
– Social interactions are simplified
• Node status {inactive, active}
• Extensions toward real-world dynamics
– Multiple campaigns
– More sophisticated social interactions
and optimization objectives

Modeling Considerations
• Which model(s) to extend?
– IC, LT, or more general ones
• How many entities
• What kinds of interactions?
– Competitions
– Cooperation (Complementarity)
– Comparative

Competitive Independent Cascade (CIC)
•
[Chen et al. “Information and Influence Propagation in Social Networks”, Morgan & Claypool 2013]

•
v
u1 u2 u3 u4
v
u1 u2 u3 u4
Competitive Independent Cascade
(CIC)

Tie-Breaking Rules
•

Competitive Linear Thresholds (CLT)
•

Influence Maximization in CIC/CLT
•

Equivalence to Live-edge Models
•

Monotonicity and Submodularity
•

Influence Blocking Maximization
•
[Budak et al. Limiting the Spread of misinformation in Social Networks]
[He at al. “Influence Blocking Maximization in Social Networks under the Competitive Linear Threshold Model”, SDM 2012]

Monotonicity and Submodularity
•

IC-N Model (Negative Opinion)
•
[Chen et al., “Influence Maximization in Social Networks When Negative Opinions May Emerge and Propagate”,
SDM 2011]

Weight-Proportional LT
•
[Borodin et al. Threshold models for competitive influence in social networks. WINE 2010.]

K-LT Model
•
[Lu et al. “The Bang for the Buck: Fair Competitive Viral Marketing from the Host Perspective”, KDD 2013]

Viral marketing as a service

Fair Allocation
•

Competition & Complementarity
• Any relationship is possible
– Compete (iPhone vs Nexus)
– Complement (iPhone & Apple Watch)
– Indifferent (iPhone & Umbrella)
• Classical economics concepts: Substitute &
complementary goods
• Item relationship may be asymmetric
• Item relationship may be to an arbitrary extent
[Lu et al. “From Competition to Complementarity: Comparative Influence Diffusion and Maximization”, KDD 2013]

Modeling Complementarity
•
[Narayanam et al. “Viral marketing for product cross-sell through social networks”, PKDD 2012]

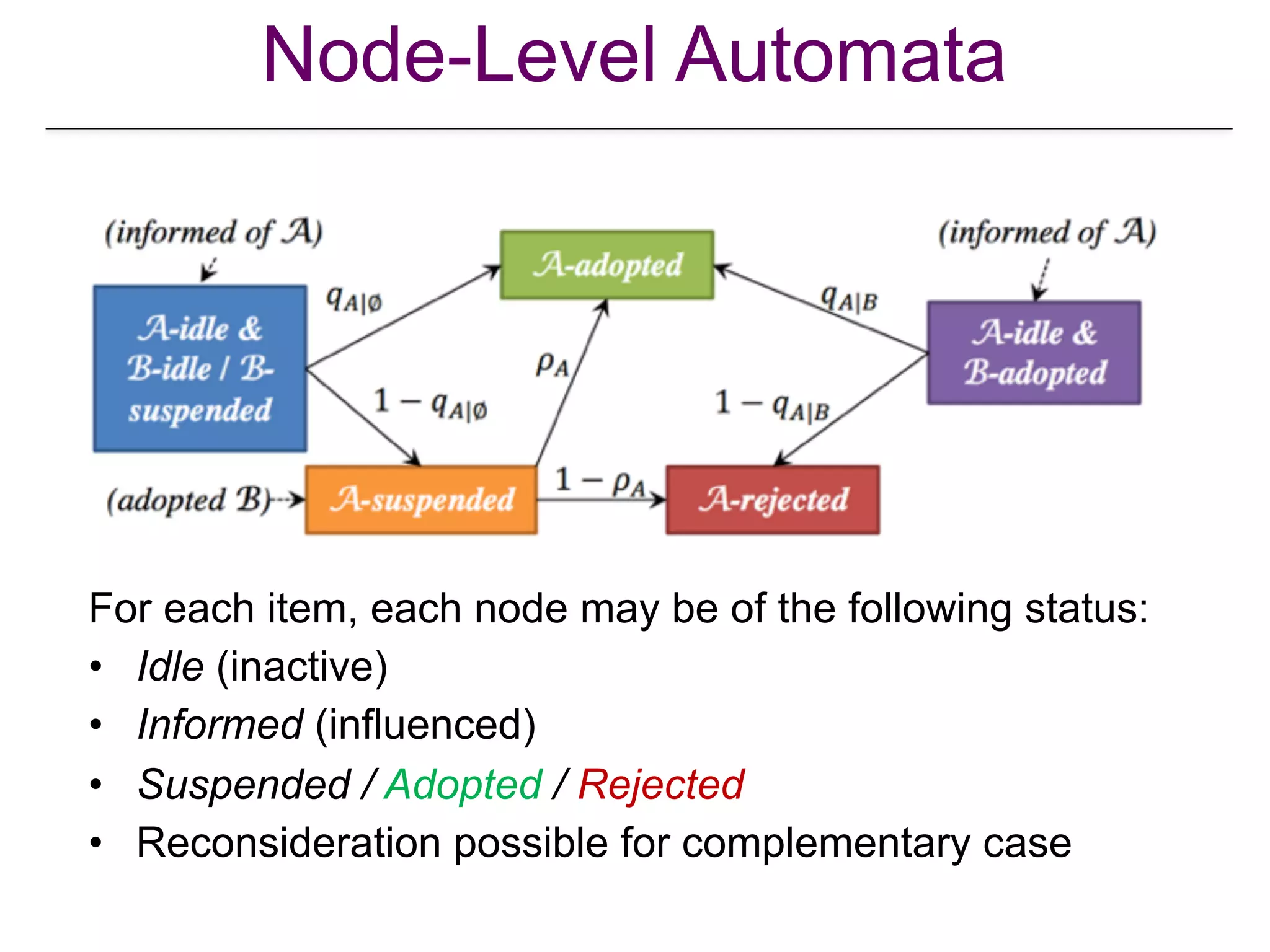
Comparative Influence Cascade (Com-IC)
• Com-IC Model: A unified model
characterizing both competition and
complementarity to arbitrary degree
• Edge-level: influence/information
propagation
• Node-level: Decision-making controlled by
an automata (“global adoption
probabilities”)

Global Adoption Probabilities
•

Node-Level Automata
For each item, each node may be of the following status:
• Idle (inactive)
• Informed (influenced)
• Suspended / Adopted / Rejected
• Reconsideration possible for complementary case

Complementarity oriented
maximization objective
•

Generalized Reverse Sampling
•

!158
Social Advertising
Social Advertising, a market that did not exist until Facebook
launched its first advertising service in May 2005, projected to
generate $11 billion revenue by the end of 2017*
Viral Marketing Meets Social Advertising!
Influence
Maximization
Computational
Advertising
* http://www.unified.com/historyofsocialadvertising/

!159
Social Advertising
Social Advertising, a market that did not exist until Facebook
launched its first advertising service in May 2005, projected to
generate $11 billion revenue by the end of 2017*
* http://www.unified.com/historyofsocialadvertising/
• Implemented by online social networking platforms
• “Promoted Posts” are injected to the social feeds of users
• Advertisers have to pay for engagements / clicks

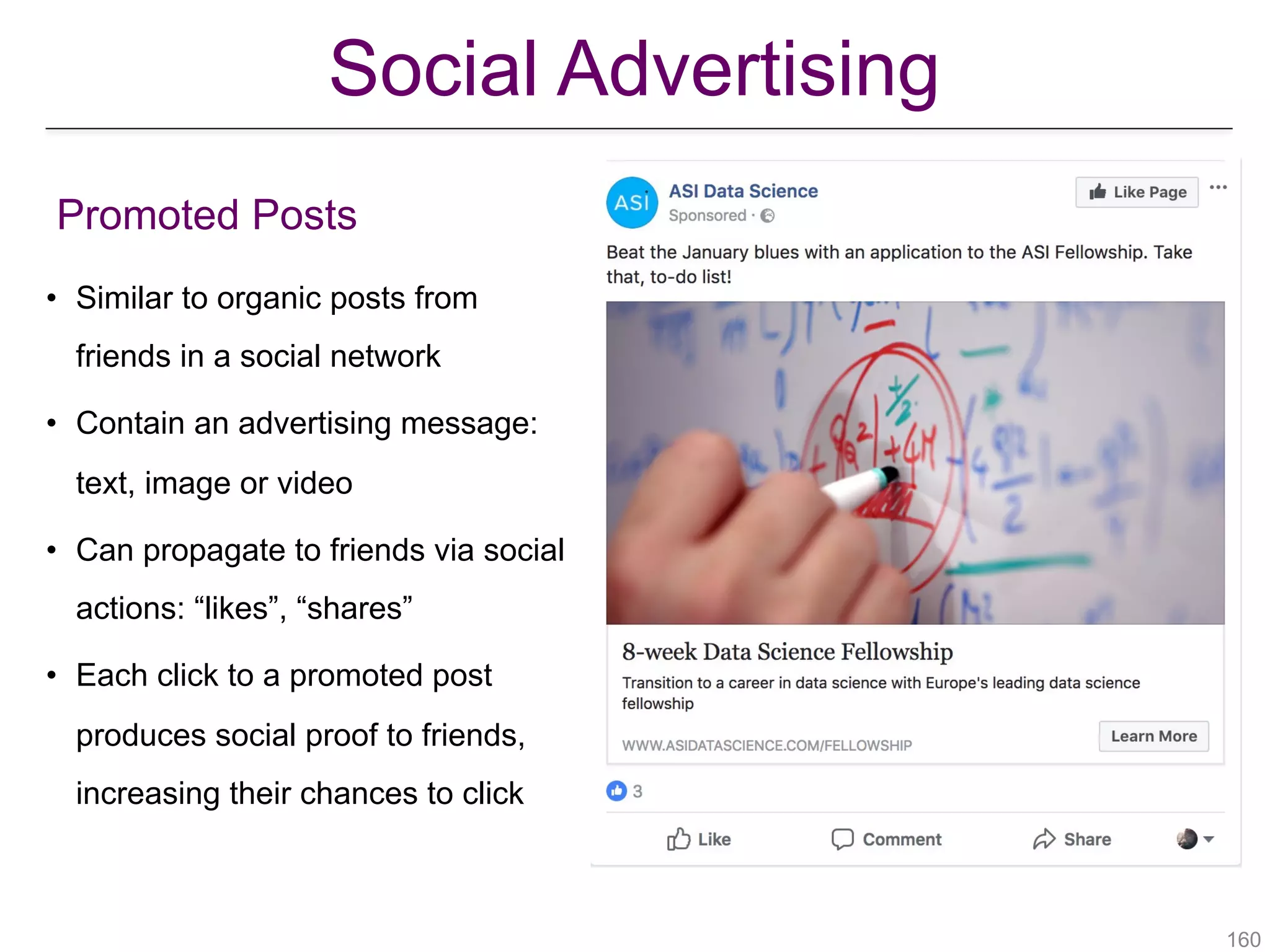
!160
Social Advertising
• Similar to organic posts from
friends in a social network
• Contain an advertising message:
text, image or video
• Can propagate to friends via social
actions: “likes”, “shares”
• Each click to a promoted post
produces social proof to friends,
increasing their chances to click
Promoted Posts

Social Advertising
Cost per Engagement (CPE) Model
• The social network platform owner (a.k.a. host)
– Sells “ad-engagements” (“clicks”) to advertisers
– Inserts promoted posts to the social feed of users likely to click
– high click-through-probability (CTP)
• Advertiser
– Has limited ``monetary” advertising budget
– Pays a fixed CPE to host for each engagement / click
!161
nice ad! indeed!

Social Advertising
!162
Ad allocation under social influence
Strategically allocate users to advertisers, leveraging social influence and
the propensity of ads to propagate, subject to limited advertisers’ budgets
Challenges
• Balance between limited advertisers’ budgets and virality of ads
• Limited attention span of online social network users
• Balance between assigning ads to users who are likely to click (i.e.,
relevant) VS who are likely to boost further propagation (i.e., influential)

• Balance between intrinsic relevance in the absence of social proof and
peer influence
• Ad-specific CTP for each user: δ(u,i)
• Probability that user u will click ad i in the absence of social proof
• TIC-CTP reduces to TIC model with pi
H,u = δ(u,i)
• When δ(u,i) = 1 for all u and i, TIC = TIC-CTP
v
u
wH
puw
puv
pHv
pHw
pHu
!163[Aslay et al., “Viral marketing meets social advertising: Ad allocation with minimum regret”, VLDB 2015]
Extending TIC model with Click-Through-Probabilities
Ad Relevance vs Social Influence

Budget and Regret
• Host:
• Owns directed social graph G = (V,E) and TIC-CTP model instance
• Sets user attention bound κu for each user u ∊ V
• Advertiser i:
• agrees to pay CPE(i) for each click up to his budget Bi
• total monetary value of the clicks πi(Si) = σi(Si) × cpe(i)
• Exp. revenue of the host from assigning seed set Si to ad i: min(πi(Si), Bi)
Host’s regret
!164
• πi(Si) < Bi : Lost revenue opportunity
• πi(Si) > Bi : Free service to the advertiser
[Aslay et al., “Viral marketing meets social advertising: Ad allocation with minimum regret”, VLDB 2015]

Budget and Regret
(Raw) Allocation Regret
• Regret of the host from allocating seed set Si to advertiser i:
Ri(Si) = |Bi − πi(Si) |
• Overall allocation regret:
R(S1, …, Sh) = Ri(Si)
Penalized Allocation Regret
• λ: penalty to discourage selecting large number of poor quality seeds
• Regret of the host with seed set size penalization
Ri(Si) = |Bi − πi(Si) | + λ × |Si|
!165
hX
i=1

Regret Minimization
• Given
• a social graph G = (V,E)
• TIC-CTP propagation model
• h advertisers with budget Bi and cpe(i) for each advertiser i
• attention bound κu for each user u ∊ V
• penalty parameter λ ≥ 0
• Find a valid allocation S = (S1, …, Sh) that minimizes the overall regret of the
host from the allocation:
!166[Aslay et al., “Viral marketing meets social advertising: Ad allocation with minimum regret”, VLDB 2015]

• Regret-Minimization is NP-hard and is NP-hard to approximate
• Reduction from 3-PARTITION problem
• Regret function is neither monotone nor submodular
• Mon. decreasing and submodular for πi(Si) < Bi and πi(Si U {u}) < Bi
• Mon. increasing and submodular for πi(Si) > Bi and πi(Si U {u}) > Bi
• Neither monotone nor submodular for πi(Si) < Bi and πi(Si U {u}) > Bi
!167
Regret Minimization
Bi
πi(Si) πi(Si U {u})

!168
• A greedy algorithm
• Select the (ad i, user u) pair that gives the max. reduction in regret at
each step, while respecting the attention constraints
• Stop the allocation to i when Ri(Si) starts to increase
• Approximation guarantees w.r.t. the total budget of all
advertisers:
• Theorem 2: for λ > 0, details omitted
• Theorem 3: for λ = 0: R(S) ≤
• Theorem 4: for λ = 0: R(S) ≤
#P-Hard
Regret Minimization
1
3
·
hX
i=1
Bi
max
i2[h],u2V
cpe(i) · i({u})
Bi
·
hX
i=1
Bi

Two-Phase Iterative Regret Minimization (TIRM)
* Tang et al., “Influence maximization: Near-optimal time complexity meets practical efficiency”, SIGMOD 2014
TIM* cannot be used for minimizing the regret
① Does not handle CTPs
② Requires predefined seed set size s
!169
Scalable Regret Minimization
• Built on the Reverse Influence Sampling framework of TIM
• RR-sets sampling under TIC-CTP model: RRC-sets
• Iterative seed set size estimation

(1) RR-sets sampling under TIC-CTP model: RRC-sets
• Sample a random RR set R for advertiser i
• Remove every node u in R with probability 1 – δ(u,i)
• Form “RRC-set” from the remaining nodes
Scalability compromised:
Requires at least 2 orders of magnitude bigger
sample size for CTP = 0.01.
Theorem 5: MG(u | S) in IC-CTP = δ(u) * MG(u | S) in IC
!170

For each advertiser i:
• Start with a “safe” initial seed set size si
• Sample θi(si) RR sets required for si
• Update si based on current regret
• Revise θi(si), sample additional RR sets, revise estimates
(2) Iterative Seed Set Size Estimation
Estimation accuracy of TIRM Theorem 6
!171

Ui(S) =
(
⇧i(Si) if ⇧i(Si)  Bi
2Bi ⇧i(Si) otherwise.
• Define utility function from
``Approximable” Regret
[Tang and Yuan, “Optimizing ad allocation in social advertising”, CIKM 2016 ]
• Regret-Minimization is NP-hard and is NP-hard to approximate
• Reduction from 3-PARTITION problem
• Regret function is neither monotone nor submodular
Bi
πi(Si) πi(Si U {u})
[Aslay et al., VLDB 2015]

!173[Tang and Yuan, “Optimizing ad allocation in social advertising”, CIKM 2016 ]
• Constant approx. under the assumption maxv i({v}) < bBi/cpe(i)c
``Approximable” Regret
Minimize
hX
i=1
|Bi ⇧i(Si)|
hX
i=1
Ui(S)
Maximize Maximize (submodular)
hX
i=1
min(Bi, ⇧i(Si))
(1/4)-approximation (1/2)-approximation*
Partition matroid• User attention bound constraint
* Fisher, et al., "An analysis of approximations for maximizing submodular set functions II." Polyhedral Combinatorics 1978
Submodular maximization
subject to matroid constraint

Sponsored Social Advertising
!174
Advertiser
• Pays a fixed CPE to host for each
engagement up to his budget
• Gives free products / discount coupons to
seed users
[Chalermsook et al., “Social network monetization via sponsored viral marketing”, SIGMETRICS 2015]
ki
min(Bi, ⇧i(Si))
• No -approximation algorithm possible unless P = NPO(n1 ✏
)
• Unlimited advertiser budgets O(log n)-approximation
maximize
(S1,··· ,Sh)
X
i2[h]
min(Bi, ⇧i(Si))
subject to |Si|  ki, 8i 2 [h]
Find an allocation S = (S1, …, Sh) maximizing the revenue of the host:

Incentivized Social Advertising
CPE Model with Seed User Incentives
!175
• Host
• Sells ad-engagements to advertisers
• Inserts promoted posts to feed of users in exchange for monetary incentives
• Seed users take a cut on the social advertising revenue
• Advertiser
• Pays a fixed CPE to host for each
engagement
• Pays monetary incentive to each seed
user engaging with his ad
• Total payment subject to his budget
[Aslay et al., “Revenue Maximization in Incentivized Social Advertising”, VLDB 2017]

• Given
• a social graph G = (V,E)
• TIC propagation model
• h advertisers with budget Bi and CPE(i) for each ad i
• seed user incentives ci(u) for each user u∈V and for each ad i
• Find an allocation S = (S1, …, Sh) maximizing the overall revenue of the
host:
!176

• Revenue-Maximization problem is NP-hard
• Restricted special case with h = 1:
• NP-Hard Submodular-Cost Submodular-Knapsack* (SCSK) problem
!177
*Iyer et al., “Submodular optimization with submodular cover and submodular knapsack constraints”, NIPS 2013.
Partition matroid
Submodular knapsack constraints
• Family 𝘊 of feasible solutions form an Independence System
• Two greedy approximation algorithms w.r.t. sensitivity to seed user
costs during the node selection

• Cost-agnostic greedy algorithm
• Selects (node,ad) pair giving the max. marginal increase in revenue
• Approximation guarantee follows* from 𝘊 forming an independence
system
where
• R and r are, respectively, upper and lower rank of 𝘊
• κπ is the curvature of total revenue function π(.)
!178
* Conforti et al., "Submodular set functions, matroids and the greedy algorithm: tight worst-case bounds and some
generalizations of the Rado-Edmonds theorem.", Discrete Applied Mathematics 1984

• Cost-sensitive greedy algorithm
• Selects the (node,ad) pair giving the max. rate of marginal gain in
revenue per marginal gain in payment
• Approximation guarantee obtained
where
• ρmax and ρmin are, respectively, max. and min. singleton payments
• κρi is the curvature of ad i’s payment function ρi(.)
!179

Two-Phase Iterative Revenue Maximization
• Built on the Reverse Influence Sampling framework of TIRM*
• Latent seed set size estimation
!180
• Two-Phase Iterative Cost-Agnostic Revenue Maximization (TI-CARM)
• Two-Phase Iterative Cost-Sensitive Revenue Maximization (TI-CSRM)

• Part I: Introduction
• Part II: Scalable Approximation Algorithms and
Extensions to Topic, Time, and Location
• Part III:
(a) Multiple Campaigns
(b) Social Advertising
• Part IV:
(a) Offline Learning of Models
(b) Online Learning of Models
(c) Summary and Open Challenges
Overview of Tutorial

!182
Modeling and Learning Social Influence
Past propagation data available?
no yes
Online Learning via
Multi-Armed Bandits
Offline Learning
from Samples

Offline Learning from Samples
• Do we know the structure of the social network?
• Do we know the time of activations?
• Can we observe the cascades fully or partially?
What is ``samples”?
What can we learn?
• Structure of the unknown network?
• Local influence parameters, i.e., edge weights?
• Global influence function, i.e., σ(S)?
(Local Learning)
(Global Learning)
(Structure Learning)

Unknown Known
Observed OLP-1 OLP-2
Unobserved GL* OLP-3
Classification of Offline Learning Problems (OLPs)
Social Network Structure
Act.Times
Offline Learning from Samples
* Good luck!
• OLP-1: Structure Learning (nice side effect: Local Learning)
• OLP-2: Local Learning
• OLP-3: Global Learning (nice side effect: Local Learning)

OLP1: Network Unknown & Activation Times Observed
• Sample = {tc}c∈D where tc = [tc(u1), …, tc(un)] is activation times in cascade c
• tc(u) = ∞ for inactive u in cascade c
• If node v tends to get activated soon after node u in many different
cascades, then (u,v) is possibly an edge in unknown G
• Local Learning is a nice side affect of Structure Learning!
Structure Learning
Actual Network Learned Network
Local Learning
[Myers & Leskovec, "On the Convexity of Latent Social Network Inference", NIPS 2010]
[Gomez-Rodriguez, Leskovec, & Krause, "Inferring networks of diffusion and influence", KDD 2010]

Structure Learning as a Convex Optimization Problem
• pvu = P(v activates u | v is active) Parameters of the
IC / SI / SIS / SIR model
• Likelihood function:
• Let denote the set of nodes in c activated before time tXc(t)
successful activations
failed activations
L(p; D) = ⇧c2D
✓
⇧
u:tc(u)<1
P(u activated at tc(u) | Xc(tc(u)))
◆
·
✓
⇧
u:tc(u)=1
P(u never active | Xc(t), 8t)
◆

• Assume probability of a successful activation decays with time
• Convexification:
• Convex program with n2 - n variables
• No guarantees wrt sample complexity!
P(u act. at tc(u) | Xc(tc(u))) = 1 ⇧
v:tc(v)tc(u)
[1 pvu · f(tc(u) tc(v))]
P(u never active | Xc(t), 8t) = ⇧
v:tc(v)<1
(1 pvu)
andc = 1 ⇧
v:tc(v)tc(u)
[1 pvu · f(tc(u) tc(v))] ✓vu = 1 pvu
• Maximize Minimizelog L(p, D) log L(✓, , D)

[Netrapalli & Sanghavi, "Learning the graph of epidemic cascades", SIGMETRICS 2012]
• Assume correlation decay instead (of time decay)
• Cascade from seed nodes do not travel far
• Average distance from a node to a seed is at most
• For any node u
X
v2Nin(u)
Avu < 1 ↵ P(tc(u) = t)  (1 ↵)t 1
pinitand
1/↵
failed activations
successful activations
correlation decay
L(p; D) = ps
init(1 pinit)n s
·
✓
⇧
u:tc(u)=1
⇧
v:tc(v)<1
(1 pvu)
◆
· ⇧c2D
✓
⇧
u:tc(u)<1
1 ⇧
v:tc(v)tc(u)
(1 pvu)
◆
• Likelihood function with s seeds

[Netrapalli & Sanghavi, "Learning the graph of epidemic cascades", SIGMETRICS 2012]
• Maximize Minimizelog L(p, D) log L(✓, D)
• Convexification: ✓vu = 1 pvu
• Decouples into n convex programs, i.e., one per node
• Activation attempts are independent in IC / SI / SIS / SIR models
• Sample complexity results as a function of pinit and
• LB for per node neighborhood recovery and learning
• LB for whole graph recovery and learning
↵

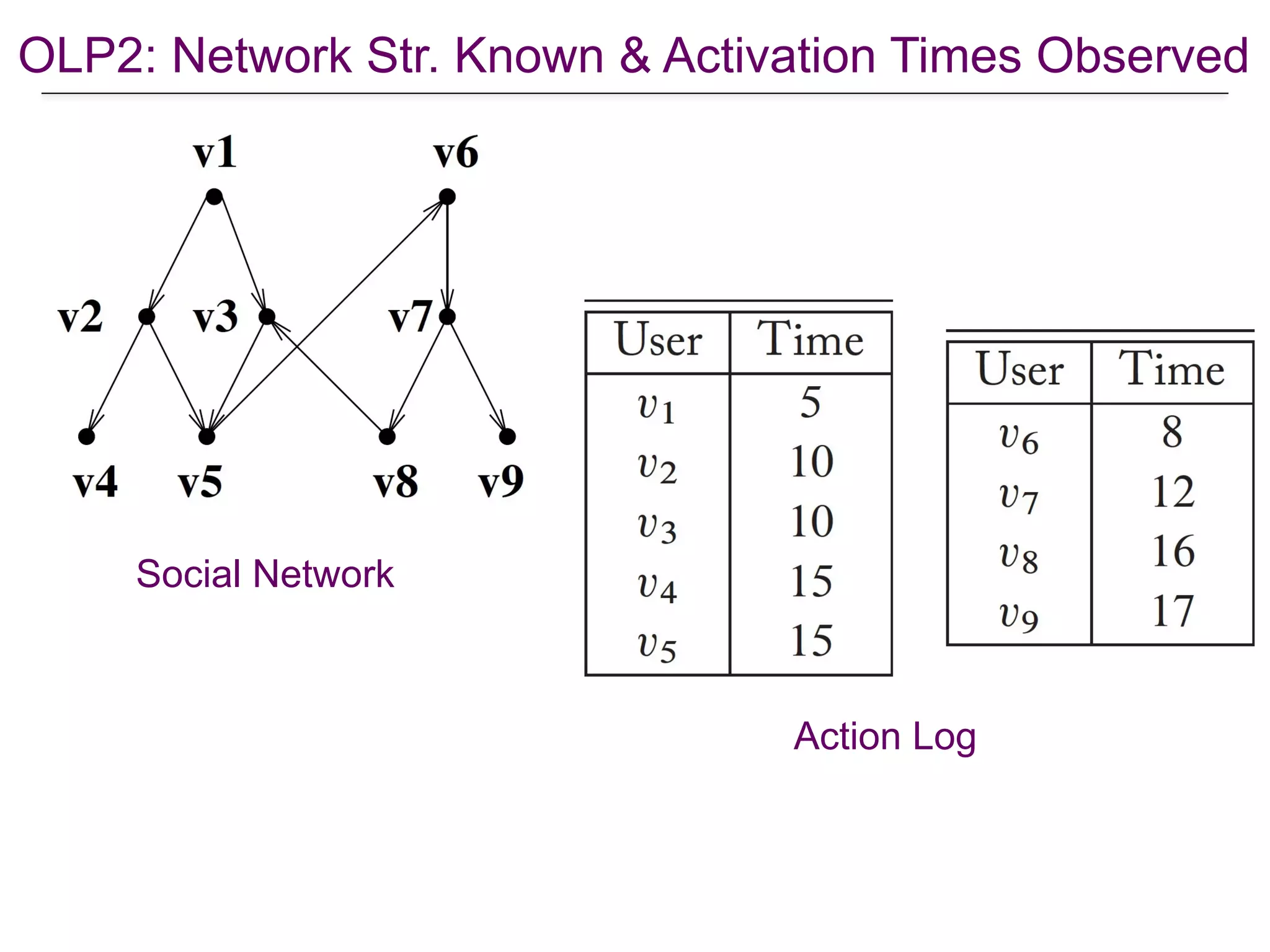
OLP2: Network Str. Known & Activation Times Observed
Social Network
Action Log

• Sample = {(Xc(0), …, Xc(T))}c∈D where Xc(t) are the nodes activated at
time t in cascade c. Define Yc(t’) = ∪t∈[1:t’] Xc(t).
• Likelihood of a single cascade c
[Saito et al., “Prediction of Information Diffusion Probabilities for Independent Cascade Model”, KES 2008]
• Use Expectation Maximization to solve L(p,D) for p
• Computationally very expensive, not scalable!
L(p, c) =
0
@
T 1Y
t=0
Y
u2Xc(t+1)
(1
Y
v2Nin(u)Yc(t)
(1 pvu))
1
A
·
0
@
T 1Y
t=0
Y
u2Xc(t)
Y
v2Nout(u)Yc(t)
(1 pvu)
1
A
success
failure
• Likelihood of D: L(p, D) =
Y
c2D
L(p, c)

• MLE procedure of Saito et al.
• Learning limited to IC model
• Assumes influence weights remain constant over time
• Accuracy depends on how well the activation times are discretized
[Goyal, Bonchi, & Lakshmanan, "Learning influence probabilities in social networks", WSDM 2010]
• A frequentist modeling approach for learning by Goyal et al.
• Active neighbor v of u remains contagious in [t, t + 𝛕(u,v)], has constant
probability puv in this interval and 0 outside
• Can Learn IC, LT, and General Threshold models
• Models are able to predict when a user will perform an action!
• Minimum possible number of scans of the propagation log with
chronologically sorted data

OLP3: Network Str. Known & Activation Times Unobserved
• Sample = {(Sc, Xc)}c∈D where Sc are the seeds of cascade c and Xc are the
complete set of active nodes in cascade c
• Interpret IC / LT influence functions as coverage functions
• Each node u reachable from seed set S is covered with certain weight au
• au : conditional probability that node u would be influenced by S
• Expected influence spread = the weighted sum of coverage weights:
[Du et al., “Influence Function Learning in Information Diffusion Networks", ICML 2014]
(S) =
X
u2[s2S Xs
au
• Sampled cascades (Sc,Xc): instantiations of random reachability matrix
• MLE for random basis approximations
• Polynomial sample complexity results wrt the desired accuracy level!

* Valiant, “A theory of the learnable”, Communications of the ACM, 1984
• PAC learning*: Probably Approximately Correct learning
• A formal framework of learning with accuracy and confidence
guarantees!
• PAC learning of IC / LT influence functions
• Sample complexity wrt the desired accuracy level and confidence
• Also solves OLP2 with learnability guarantees!
[Narasimhan, Parkes, & Singer, "Learnability of Influence in Networks", NIPS 2015]
Influence functions are PAC learnable!
• Influence function F : 2V → [0,1]n
• For a given seed set S
F(S) = [F1(S), …, Fn(S)]
• Fu(S) is the probability of u being influence during any time step

• FG: class of all influence functions over G for different parametrization
• The seeds of cascades are drawn iid from a distribution
• Measuring error from expected loss over random draws of S and X:
error[F] = ES,X[loss(X, F(S))]
PAC learnability of influence functions
µ
discrepancy between predicted and observed
• Goal: learn a function FD ∈ FG that best explains the sample D:
probably
P(error[FD] inf
F 2FG
error[F]  ✏) 1
approximately

• LT influence functions as multi-layer
neural network classifiers
• Linear threshold activations
• Local influence as a two-layer NN
• Extension to multiple-layer NN by
replicating the output layer
LT model
• Learnability guarantees follow from neural-network classifiers
• Finite VC dimension of NNs implies PAC-learnability

LT model
• Exact solution gives zero training error on the sample
• Due to deterministic nature of LT functions
• Is computationally very hard to solve exactly
• Equivalent to learning a recurrent neural network
• Approximations possible by
• Replacing threshold activations with sigmoidal activations
• Using continuous surrogate loss instead of binary loss function
• Exact polynomial time learning possible when there is also the
activation times!

• IC influence function as expectation over a random draw of a subgraph A
• Let Fp denote the global IC function for parametrization p
IC model
• Define the global log-likelihood for cascade c = (Sc, Xc):
Fp
u (S) =
X
A✓E
Y
(a,b)2A
pab ·
Y
(a,b)62A
(1 pab) · 1(S reaches u in A)
L(Sc
, Xc
, p) =
nX
u=1
1(u2Xc) log Fp
u (S) + (1 1(u2Xc)) log(1 Fp
u (S))
success failure

IC model
max
p2[ ,1 ]m
X
c2D
L(Sc
, Xc
, p)
• Learnability follows from standard uniform convergence arguments
• Construct an ∊-cover of the space
• Use Lipschitzness to translate this to ∊-cover of IC function class
• Uniform convergence implies PAC learnability
[ , 1 ]
• MLE of the overall log-likelihood to obtain p
kp p0
k  ✏ |Fp
u (S) Fp0
u (S)|  ✏
• Use Lipschitzness (i.e., bounded-derivative) property of IC function
class to obtain Fp from p with guarantees

• Sample = {(Sc, Xc)}c∈D where Sc are the seeds of cascade c and Xc are
the ``complete” set of active nodes in cascade c
• What if the cascades are not ``complete”?
• When using Twitter API to collect cascades
• Solution: Adjust the distributional assumptions of the PAC learning
framework!
• Partially observed cascades Xc are drawn from a distribution over
the random activations of Sc
[He, Xu, Kempe, & Liu., “Learning Influence Functions from Incomplete Observations”, NIPS 2016]
over seeds

• PAC learning with two distributional assumptions
• Partially observed cascades Xc are drawn from a distribution over
the random activations of Sc
• Extension of Narasimhan et al.’s methods are not efficient with the
additional distributional assumptions (on Xc)
• PAC learning of random reachability matrix
• Learning model-free coverage functions as defined by Du et al.*
• Polynomial sample complexity for solving (only) OLP3
[He, Xu, Kempe, & Liu., “Learning Influence Functions from Incomplete Observations”, NIPS 2016]
* Du et al., “Influence Function Learning in Information Diffusion Networks", ICML 2014

• Influence functions are PAC learnable from samples but the
influence maximization from samples is intractable
• Requires exponentially many samples
• No algorithm can provide constant-factor approximation
guarantee using polynomially many samples
How about directly solving the influence maximization problem
directly from a given sample??
Solving IM from Samples
[Balkanski, Rubinstein, and Singer. “The limitations of optimization from samples”, STOC 2017]

[Goyal, Bonchi, & Lakshmanan, "A data-based approach to social influence maximization", VLDB 2011]
A frequentist mining approach

• Instead of learning the probabilities and simulating propagations, use
available propagations to estimate the expected spread
[Goyal, Bonchi, & Lakshmanan, "A data-based approach to social influence maximization", VLDB 2011]
A frequentist mining approach
(S) =
X
u2V
E[path(S, u)] =
X
u2V
P[path(S, u) = 1]
• We cannot estimate directly P[path(S,u)] from the sample
• Sparsity issues where S is effectively the seed of a cascade
• Take a u-centric perspective instead:
• Each time u performs an action, distribute the ``influence credit”
• Resulting credit distribution model is submodular
• Find the top-k seed from the sample via greedy algorithm
• Very efficient but no formal guarantees wrt the ``real optimal seed set”

• Leverage strong community structures of social networks
• Identify a set of users who are influentials but whose communities
have little overlap
• Define a tolerance parameter α for the allowed community overlap
• Greedy algorithm to find top-k seeds wrt allowed overlap
A formal but constrained approach
P
Sc⇠µ,8c2D
[E[f(S)] ↵ max
T ✓V
f(T)] 1
• First formal way to optimize IC functions from samples!
[Balkanski, Immorlica, & Singer, “The Importance of Communities for Learning to Influence", NIPS 2017]

Learning Influence Probabilities
• Off-line learning: Given a batch of
cascade events (timestamped user
actions) as input, and learn the edge
probabilities
• On-line learning
– No log data available
– Generating learning data while learning
– Typical objective: minimize “regret”

Multi-Armed Bandits (MAB)
•
[Audibert et al. “Introduction to Bandits: Algorithm and Theory”, ICML 2011]

Exploration & Exploitation
•

UCB Strategy
•

Combinatorial Multi-Armed Bandits
•

CMAB in Influence Maximization
•

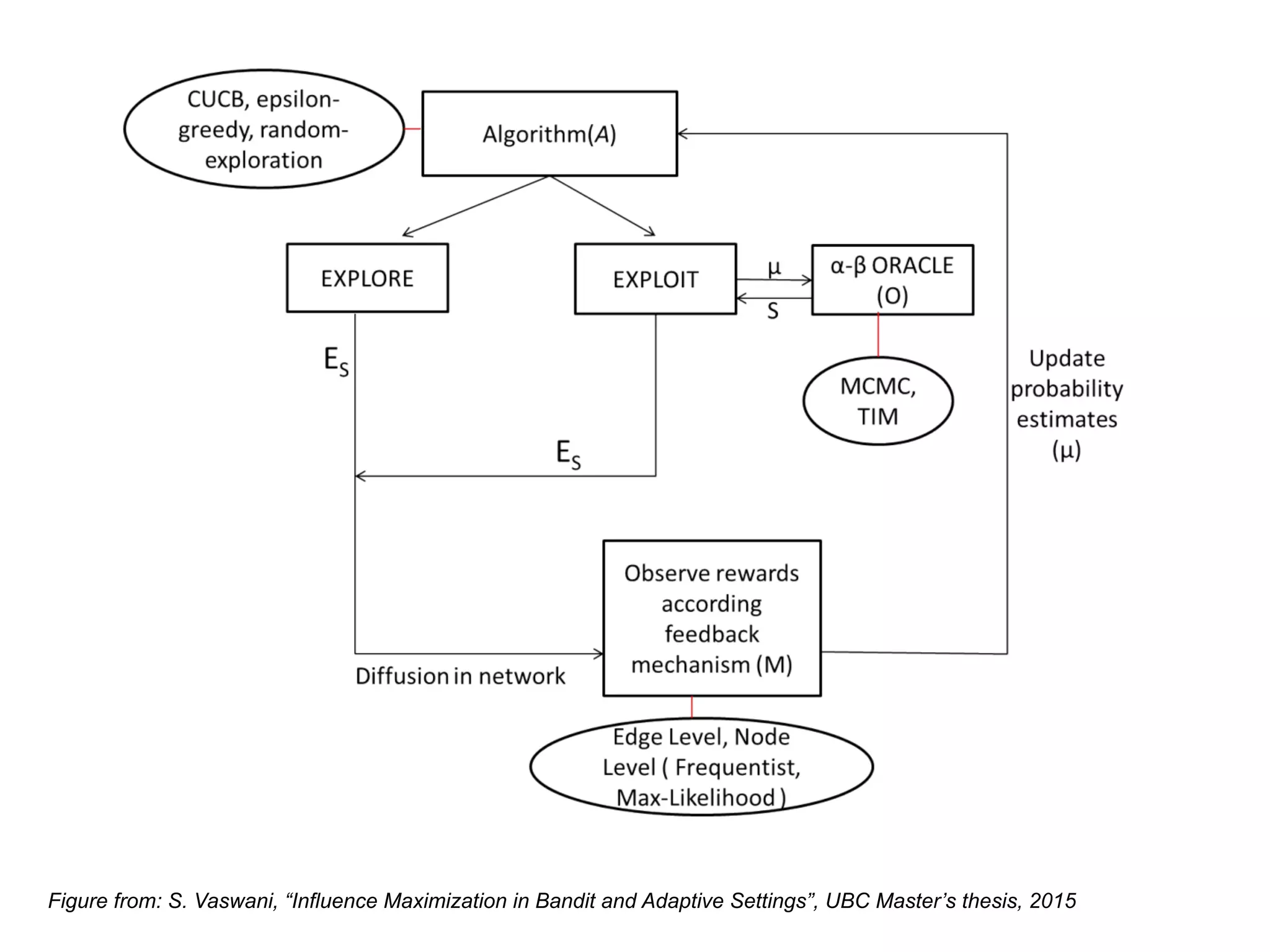
Figure from: S. Vaswani, “Influence Maximization in Bandit and Adaptive Settings”, UBC Master’s thesis, 2015

Explore-Exploit in Online IM
•
[Lei et al. “Online Influence Maximization”, KDD 2015]

Linear Representation
•
*Wen et al, “Online Influence Maximization under Independent Cascade Model with Semi-Bandit Feedback”, NIPS 2017.
^Vaswani et al., “Model-independent Online Learning for Influence Maximization”, ICML 2017

Adaptive Influence Maximization
• Selecting all seeds at once (non-adaptive)
vs. one at a time (adaptive)
Figure from: S. Vaswani, “Influence Maximization in Bandit and Adaptive
Settings”, UBC Master’s thesis, 2015

Adaptive Influence Maximization
• IM becomes a problem of active learning
• Selecting the next best seed requires a
policy that depends on
– Graph structure and influence
probabilities (as in non-adaptive IM)
– State of the graph in each step (edge
revelations)
• Key contribution: Extending submodularity
to adaptive setting*
*Golovin et al., “Adaptive Submodularity: Theory and Application in Active Learning and Stochastic Optimization”, JAIR 2011.

Open Challenges
• Design more efficient RR-set based
algorithms for high influence networks
• Design incentive-compatible (truthful)
social advertising mechanisms
• IM in the wild: How to learn network &
model? How to interface with real world?
• Emerging IM applications in science (yeast
cell). More? General paradigm?

WSDM 2018 Tutorial on Influence Maximization in Online Social Networks

More Related Content

What's hot

Similar to WSDM 2018 Tutorial on Influence Maximization in Online Social Networks

Recently uploaded

In this document

WSDM 2018 Tutorial on Influence Maximization in Online Social Networks