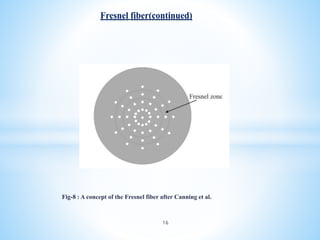
Photonic crystal fiber (PCF) uses a periodic arrangement of air holes in the cladding around a solid core or hollow core to guide light. PCFs offer several advantages over traditional optical fibers, including the ability to design fibers that are endlessly single mode, have zero dispersion in visible wavelengths, and high nonlinearities. They can also be engineered to have special properties like high birefringence, dispersion compensation, large mode areas, and sensing capabilities. Key applications of PCF include telecommunications, fiber lasers, nonlinear devices, high power transmission, and chemical/biological sensing.

1. 1
What is PCF??
 The idea of a photonic crystal fiber was presented for the first time by Yeh et
al. in 1978.
 A photonic crystal fiber made of 2D photonic crystal with an air core was
invented by P. Russell in 1992 and the first PCF was reported at the Optical
Fiber Conference (OFC) in 1996 .
 Photonic crystal fiber (PCF) is a kind of optical fiber that uses
photonic crystals to form the cladding around the core of the cable.
 Photonic crystal fibers (PCFs) are fibers with an internal periodic structure
made of capillaries, filled with air, laid to form a hexagonal lattice.
 lattice pitch, air hole shape and diameter, refractive index of the glass, and type
of lattice determines the properties of the fiber.

2. CFs Solid-core :
 solid-core PCF’s guide light by Total Internal Reflection (TIR) at the boundary between a
low index cladding and a high index core.
 The solid core class of fibers has a high-index solid core with a lower effective index
surrounding medium.
 Total internal reflection at boundary between high index solid core and lower “average”
index between air and glass index photonic crystal cladding
* Types of PCF
2

3. Hollow core fibers:
 A photonic band gap in the cladding acts as a virtually loss-free mirror confining light to a
core that does not necessarily have to consist of solid material.
 The hollow core fibers have a lower index than the surrounding medium, and confinement
to the center core hole is made possible by scattering and interference, combining to form
an evanescent field in the cladding region.
3

4. Endlessly single mode fibers
 PCF can be designed so that they are single mode for a large range of visual and near infrared
spectrum.
 Classical step index fibers (SIFs) always have a cut-off frequency above which the fibers starts to
be multimode.
 To determine the number of guided modes in SIF usually a normalized frequency V is used. V is
defined as:
 where ρ is the core radius, ncore and ncladding are refractive indexes of the core and the cladding,
respectively.
* Properties of single mode photonic crystal fibers
4

5.  In the case of standard fibers, the cladding index is almost wavelength independent and V increases when
wavelength decreases. It results in multimode operation regime for cut-off normalized frequency higher
than 2.405.
Fig. 1. Modal properties of endlessly single mode PCF made of multicomponent glass.
Endlessly single mode fibers(continued)
5

6. Fig. 2. Normalized frequency for hexagonal lattice PCF, filling factor 0.20
* Endlessly single mode fibers(continued)
6

7. Fig3: Typical structure of a single mode PCF. Fiber fabricated at IEMT. Endlessly single mode PCF has a filling
factor less that 0.2
 With a proper design it is possible to keep V below a cut-off normalized frequency for any
wavelength range (fig-2)
 The PCF, that fulfills this condition, is usually named as endlessly single mode. A cut-off normalized
frequency for PCF has been estimated as 2.5
 A typical structure of endlessly single mode fiber is presented in Fig. 3.
Endlessly single mode fibers(continued)
7

8.  In SIFs the total dispersion comes from material and waveguide dispersion.
 A key parameter that describes properties of fibers is a group velocity dispersion (GVD). It is
defined as:
 Dispersion characteristics in PCFs can be easily shaped due to the flexibility of varying air
hole size and the position in the photonic cladding.
 waveguide dispersion can be very strong
 The material dispersion" is modified by artificial photonic cladding with the presence of air-
holes.
 Varying Λ and air-hole sizes in PCFs a zero-dispersion wavelength can be shifted into the
visible region. it automatically gives a positive (anomalous) dispersion in the visible range=>
Can be used for Compensation in telecommunication lines.
Dispersion properties
8

9. Fig 4: A comparison of dispersion in SIF and in an index-guiding PCF.
 PCF with a positive dispersion can be used for dispersion compensation in the telecommunication
lines.
Dispersion properties (continued)…
9

10.  Structures with two or more cores made with traditional step-index technology are useful in many
applications like, for example, directional couplers, wavelength multiplexers/de multiplexers, and
band sensors.
 Multi capillary fabrication technique it is easier to form multi-core PCF structures than the
traditional step-index ones.
 Two solid cores are separated by a single air hole.
Fig. 5. The cross-sections of the double-core PCF fiber with a square lattice, fiber’s diameter of 220 µm, the
lattices constant of Λ = 1.81, the hole diameter d = 0.61 µm (d/Λ = 0.34) and the central hole diameter dc = 0.45
µm. The samples fabricated at IEMT.
Double-core fibers
10

11.  Due to non-axisymmetric distribution of the effective refraction index that depends on the size and
spatial distribution of holes
 Extremely high birefringence in comparison to standard optical fibers
 A highly birefringent dispersion compensating microstructure optical fiber (MOF)
 Highly insensitive to temperature => Sensing applications
 Due to this immunity highly birefringent PCFs are very attractive for sensing and for
telecommunication applications as a compensator of polarization mode dispersion in fiber lines.
Highly birefringent fibers
11

12. Fig. 6. Examples of highly birefringent PCF: (a) HB PCF with hexagonal lattice and circular holes (b) test
samples of rectangular-shape HB PCF with rectangular lattice and elliptical holes of IEMT.
* Highly birefringent fibers(continued)
12

13.  Conventional SIFs lasers :core and double cladding made of different materials most typically with a
polymer outer cladding.
 Effciency of these devices is limited by core size, numerical aperture, and Raman scattering in
doped silica.
 Double clad of PCF : The inner cladding ensures a high NA and is surrounded with a web of silica
bridges which are substantially narrower than the wavelength of the guided radiation.
 Air-clad fiber with high NA : the diameter of the inner cladding (pump core) can be significantly
reduced while brightness acceptance of the pump radiation is kept.
 Due to high ratio of active core area to inner cladding (pump core), the pump light absorption is
improved. It allows us to use inexpensive, high power broad area emitting pumps.
* Fiber lasers and amplifiers
13

14.  Large mode area for the single mode signal allows one to obtain a high power output with
relatively low power density.
 Highly efficient lasers ….
Fig7: Double clad PCF (after Limpert et al. [51]). A solid core is surrounded with low filling factor cladding (inner
one), which plays a role of a pump core since the pump field is confined by a second high filling factor cladding
(outer one).
* Fiber lasers and amplifiers (continued)
14

15.  Free-space diffraction limit in propagation of high intensity light.
 Very diffcult to generate Bessel wave (diffraction less free-space waveform) beyond the Raighley
range of conventional optics.
 Micro-structured fiber technique :Fresnel zones determined by the ring of holes spaced at radii
such that interstitial hole spacing can be significantly larger than the propagation wavelength.
 The concentric rings of holes (Fresnel zones) have various effective refractive indexes and
interferes constructively, forming a peak field intensity in the center of the fiber axis. This enables
focusing light at the output of the fiber at the far field without any additional lens, while in
conventional fibers, light emerging from a fiber diffracts and expands.
* Fresnel fiber
15

16. Fig-8 : A concept of the Fresnel fiber after Canning et al.
Fresnel fiber(continued)
16

17.  The design of PCFs is very flexible.
 There are several parameters to manipulate:
I. lattice pitch,
II. air hole shape and diameter,
III. refractive index of the glass, and
IV. type of lattice.
 Freedom of design allows one to obtain endlessly single mode fibers, which are single
mode in all optical range and a cut-off wavelength does not exist.
 PCFs having zero, low, or anomalous dispersion at visible wavelengths can be designed
and fabricated. The dispersion can also be flattened over a very large range. Combining
anomalous dispersion with small mode field areas results in outstanding nonlinear fibers.
Designing issues of PCF
17

18. Effective Area
 Effective area is the fiber area that covers transverse dimension of the fiber.
 A low effective area provides high density of power in the core region required for non-
linear effects to be significant.
 The effective area can also be related to spot-size, with the Gaussian width w, though.
 The effective mode area A eff can be defined as –
 Here, the effective mode area A eff in μm2 and electric field amplitude is E in the
medium
* Optical Properties
18

19. propagation constant
 The propagation constant of an electromagnetic wave is a measure of the change undergone by the
amplitude of the wave as it propagates in a given direction.
 The propagation constant β is given by
 where, n eff is the effective refractive index and λ is the wavelength of the input light.
19

20. Confinement loss
 The loss in light confinement due to the periodic arrangement of cladding in PCF is called the
confinement loss.
 Confinement loss is calculated from the following equation—
 where, K 0 = 2π/ λ and it is the propagation constant in free space and Im (n eff ) is the imaginary part
of effective refractive index.
20

21. waveguide dispersion
 When the fraction of light power propagating through the cladding region faster than the core region,
then waveguide dispersion occurs.
 Waveguide dispersion is calculated from the following equation—
 where, λ is the wavelength and c is the velocity of light in free space.
21

22. Relative sensitivity
 Relative sensitivity is the ration of refractive index of sensing liquid and effective mode
index
 For calculating relative sensitivity equation is given below
 Here nr represents refractive index of sensing liquid and neff is effective mode index.
22

23.  Many physical properties can be engineered (power fraction, birefringence, chromatic
dispersion,…)
 The waveguide dispersion can be engineered to have the zero dispersion wavelength at any
desired wavelength. This is useful for nonlinear applications, where normal dispersion is a
limiting factor.
 By changing the core diameter of fiber, the Zero Dispersion Wavelength can be shifted to the
visible range.
 PCF can be filled with gases or liquids for sensing
Advantages of PCF
23

24.  Endlessly single mode fiber
 Zero Dispersion Photonic Crystal fiber
 Sensing application of PCF using LPFG
 Fiber – optic communications
 Fiber lasers
 Nonlinear devices
 High-power transmission
Applications of PCF
24