Alberto Pardo Milanés, profile picture
Uploaded byAlberto Pardo Milanés
PDF, PPTX364 views

Unit9

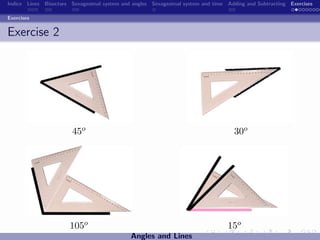
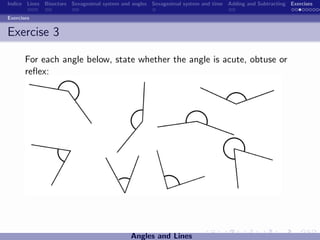
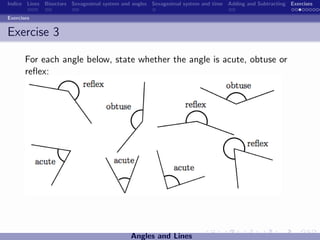
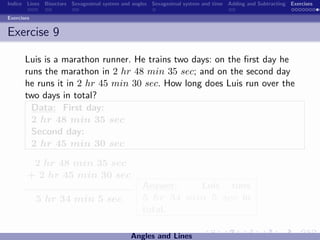
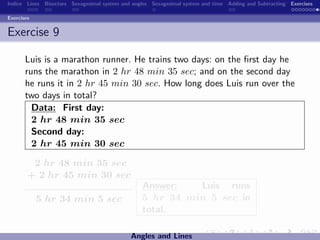
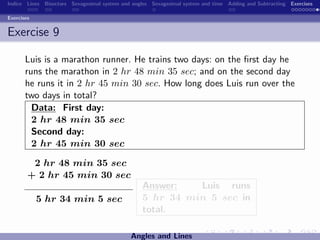
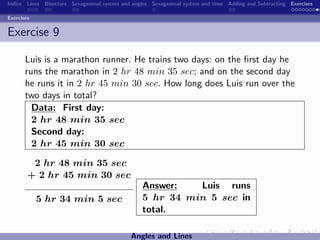
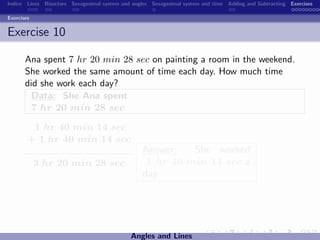
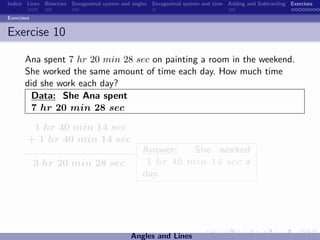
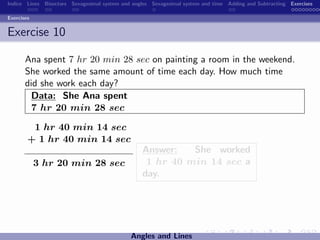
The document discusses the sexagesimal system for measuring angles and time. It explains that angles are measured in degrees, minutes, and seconds, with one degree equal to 60 minutes and one minute equal to 60 seconds. Similarly, time is measured in hours, minutes, and seconds, with one hour equal to 60 minutes and one minute equal to 60 seconds. Examples are provided to illustrate how to write angles and time measurements using this sexagesimal numeral system.

Embed presentation

Download as PDF, PPTX
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Angles and Lines Matem´ticas 1o E.S.O. a -
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises 1 Lines 2 Perpendicular bisector of a segment and bisector of an angle 3 Sexagesimal system and angles 4 Sexagesimal system and time 5 Adding and Subtracting in the sexagesimal system 6 Exercises Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Lines Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Lines Plane Geometry Plane Geometry deals with figures in a plane (circles, lines, polygons. . . ) A line is a set of points extending in two opposite directions without end, It’s a straight one-dimensional figure with no thickness and extending infinitely in both directions. A line is sometimes called a straight line. Points are said to be collinear points if they lie on a single straight line. A plane is a flat surface that has no thickness and extends without ending in ALL directions. Points are said to be coplanar points if they lie on a common plane. A line segment is a finite portion of an infinite line. A line segment always has a beginning and an end. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Lines Plane Geometry Plane Geometry deals with figures in a plane (circles, lines, polygons. . . ) A line is a set of points extending in two opposite directions without end, It’s a straight one-dimensional figure with no thickness and extending infinitely in both directions. A line is sometimes called a straight line. Points are said to be collinear points if they lie on a single straight line. A plane is a flat surface that has no thickness and extends without ending in ALL directions. Points are said to be coplanar points if they lie on a common plane. A line segment is a finite portion of an infinite line. A line segment always has a beginning and an end. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Lines Perpendicular bisector of a segment and bisector of an angle Lines that intersect in a point are called intersecting lines. Lines that do not intersect are called parallel lines (in the plane). Two lines that lie on top of one another are called coincident lines. Two lines or line segments which are perpendicular are said to be orthogonal (two lines are said to be perpendicular if they meet at a 90o angle). Given two intersecting lines, the point of intersection is called the vertex and the amount of rotation about the vertex required to bring one line into correspondence with the other is called the angle between them. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Lines One full rotation corresponds to 360 degrees. Half a full rotation is called a straight angle, and a quarter of a full rotation is called a right angle. An angle less than a right angle is called an acute angle, an angle greater than a right angle (but less than a straight angle) is called an obtuse angle, and an angle greater than a straight angle (but less than a full angle) is called a reflex angle. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Perpendicular bisector of a segment and bisector of an angle Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Perpendicular bisector of a segment and bisector of an angle Bisector of a line segment A perpendicular bisector of a line segment AB is a line perpendicular to AB and passing through the midpoint M of AB. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Perpendicular bisector of a segment and bisector of an angle Bisector of an angle The bisector of an angle is the line that divides the angle into two equal parts. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and angles Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and angles The size of an angle There are several ways to measure the size of an angle, for example using units of degrees: In a complete circle there are three hundred and sixty degrees. You can express angles to any precision using decimal numbers. Example: 30 degrees and a half is 30.5 degrees. There is another way to state the size of an angle, subdividing a degree. The degree is divided into sixty parts called minutes. These minutes are further divided into sixty parts called seconds. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and angles The size of an angle There are several ways to measure the size of an angle, for example using units of degrees: In a complete circle there are three hundred and sixty degrees. You can express angles to any precision using decimal numbers. Example: 30 degrees and a half is 30.5 degrees. There is another way to state the size of an angle, subdividing a degree. The degree is divided into sixty parts called minutes. These minutes are further divided into sixty parts called seconds. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and angles Angles: Degrees, minutes and seconds In a full circle there are 360 degrees, each degree is split up into 60 parts called minutes (each part being 1/60 of a degree), each minute is split up into 60 parts called seconds (each part being 1/60 of a minute). Example: 40 degrees, 20 minutes and 50 seconds is usually written this way: 40o 20 50 . Example: 30.5 degrees is 30o and 30 , because 0.5 degrees are 0.5 · 60 = 30 minutes. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and angles Angles: Degrees, minutes and seconds In a full circle there are 360 degrees, each degree is split up into 60 parts called minutes (each part being 1/60 of a degree), each minute is split up into 60 parts called seconds (each part being 1/60 of a minute). Example: 40 degrees, 20 minutes and 50 seconds is usually written this way: 40o 20 50 . Example: 30.5 degrees is 30o and 30 , because 0.5 degrees are 0.5 · 60 = 30 minutes. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and time Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and time Time: Hours, minutes and seconds To measure time we can use hours: In a day there are twenty-four hours. You can express time to any precision using decimal numbers. Example: 3 hours and a quarter is 3.25 hours. There is another way to state the amount of time, subdividing an hour. The hour is divided into sixty parts called minutes. These minutes are further divided into sixty parts called seconds. In a day there are 24 hours, each hour is split up into 60 parts called minutes (each part being 1/60 of an hour), each minute is split up into 60 parts called seconds (each part being 1/60 of a minute). Example: 14 hours, 56 minutes and 12 seconds is usually written this way: 14 hr 56 min 12 sec. Example: 3.25 hours is 3 hr and 15 min, because 0.25 hours are 0.25 · 60 = 15 minutes. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and time Time: Hours, minutes and seconds To measure time we can use hours: In a day there are twenty-four hours. You can express time to any precision using decimal numbers. Example: 3 hours and a quarter is 3.25 hours. There is another way to state the amount of time, subdividing an hour. The hour is divided into sixty parts called minutes. These minutes are further divided into sixty parts called seconds. In a day there are 24 hours, each hour is split up into 60 parts called minutes (each part being 1/60 of an hour), each minute is split up into 60 parts called seconds (each part being 1/60 of a minute). Example: 14 hours, 56 minutes and 12 seconds is usually written this way: 14 hr 56 min 12 sec. Example: 3.25 hours is 3 hr and 15 min, because 0.25 hours are 0.25 · 60 = 15 minutes. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and time Time: Hours, minutes and seconds To measure time we can use hours: In a day there are twenty-four hours. You can express time to any precision using decimal numbers. Example: 3 hours and a quarter is 3.25 hours. There is another way to state the amount of time, subdividing an hour. The hour is divided into sixty parts called minutes. These minutes are further divided into sixty parts called seconds. In a day there are 24 hours, each hour is split up into 60 parts called minutes (each part being 1/60 of an hour), each minute is split up into 60 parts called seconds (each part being 1/60 of a minute). Example: 14 hours, 56 minutes and 12 seconds is usually written this way: 14 hr 56 min 12 sec. Example: 3.25 hours is 3 hr and 15 min, because 0.25 hours are 0.25 · 60 = 15 minutes. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Add in the sexagesimal system You must add or subtract the units separately. But you may need to do some adjusting if the hours end up 24 or more, the minutes end up 60 or more, the seconds end up 60 or more,or less than zero. Adding Add the hours. If the hours are 24 or more, subtract 24 from the hours and add 1 to the days. Add the minutes. If the minutes are 60 or more, subtract 60 from the hours and add 1 to the hours. And so on. Example: 40o 20 50 + 10o 33 6 = 50o 55 56 . Example: 14 hr 20 min 50 sec + 15 hr 43 min 26 sec =29 hr 63 min 76 sec =1 day 6 hr 4 min 16 sec. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Add in the sexagesimal system You must add or subtract the units separately. But you may need to do some adjusting if the hours end up 24 or more, the minutes end up 60 or more, the seconds end up 60 or more,or less than zero. Adding Add the hours. If the hours are 24 or more, subtract 24 from the hours and add 1 to the days. Add the minutes. If the minutes are 60 or more, subtract 60 from the hours and add 1 to the hours. And so on. Example: 40o 20 50 + 10o 33 6 = 50o 55 56 . Example: 14 hr 20 min 50 sec + 15 hr 43 min 26 sec =29 hr 63 min 76 sec =1 day 6 hr 4 min 16 sec. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Add in the sexagesimal system You must add or subtract the units separately. But you may need to do some adjusting if the hours end up 24 or more, the minutes end up 60 or more, the seconds end up 60 or more,or less than zero. Adding Add the hours. If the hours are 24 or more, subtract 24 from the hours and add 1 to the days. Add the minutes. If the minutes are 60 or more, subtract 60 from the hours and add 1 to the hours. And so on. Example: 40o 20 50 + 10o 33 6 = 50o 55 56 . Example: 14 hr 20 min 50 sec + 15 hr 43 min 26 sec =29 hr 63 min 76 sec =1 day 6 hr 4 min 16 sec. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Add in the sexagesimal system You must add or subtract the units separately. But you may need to do some adjusting if the hours end up 24 or more, the minutes end up 60 or more, the seconds end up 60 or more,or less than zero. Adding Add the hours. If the hours are 24 or more, subtract 24 from the hours and add 1 to the days. Add the minutes. If the minutes are 60 or more, subtract 60 from the hours and add 1 to the hours. And so on. Example: 40o 20 50 + 10o 33 6 = 50o 55 56 . Example: 14 hr 20 min 50 sec + 15 hr 43 min 26 sec =29 hr 63 min 76 sec =1 day 6 hr 4 min 16 sec. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Subtract in the sexagesimal system Subtracting Subtract the hours. If the hours are negative, add 24 to the hours and subtract 1 from days. Subtract the minutes. If the minutes are negative, add 60 to the minutes and subtract 1 from hours. And so on. Example: 23 hr 40 min 51 sec − 15 hr 33 min 21 sec = 8 hr 7 min 30 sec. Example: 45o 33 12 −11o 42 20 =44o 92 72 −11o 42 20 =33o 50 52 . Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Subtract in the sexagesimal system Subtracting Subtract the hours. If the hours are negative, add 24 to the hours and subtract 1 from days. Subtract the minutes. If the minutes are negative, add 60 to the minutes and subtract 1 from hours. And so on. Example: 23 hr 40 min 51 sec − 15 hr 33 min 21 sec = 8 hr 7 min 30 sec. Example: 45o 33 12 −11o 42 20 =44o 92 72 −11o 42 20 =33o 50 52 . Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Subtract in the sexagesimal system Subtracting Subtract the hours. If the hours are negative, add 24 to the hours and subtract 1 from days. Subtract the minutes. If the minutes are negative, add 60 to the minutes and subtract 1 from hours. And so on. Example: 23 hr 40 min 51 sec − 15 hr 33 min 21 sec = 8 hr 7 min 30 sec. Example: 45o 33 12 −11o 42 20 =44o 92 72 −11o 42 20 =33o 50 52 . Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Subtract in the sexagesimal system Subtracting Subtract the hours. If the hours are negative, add 24 to the hours and subtract 1 from days. Subtract the minutes. If the minutes are negative, add 60 to the minutes and subtract 1 from hours. And so on. Example: 23 hr 40 min 51 sec − 15 hr 33 min 21 sec = 8 hr 7 min 30 sec. Example: 45o 33 12 −11o 42 20 =44o 92 72 −11o 42 20 =33o 50 52 . Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Subtract in the sexagesimal system Subtracting Subtract the hours. If the hours are negative, add 24 to the hours and subtract 1 from days. Subtract the minutes. If the minutes are negative, add 60 to the minutes and subtract 1 from hours. And so on. Example: 23 hr 40 min 51 sec − 15 hr 33 min 21 sec = 8 hr 7 min 30 sec. Example: 45o 33 12 −11o 42 20 =44o 92 72 −11o 42 20 =33o 50 52 . Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 1 Find five objects in your classroom that have right angles: Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 1 Find five objects in your classroom that have right angles: Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 2 Using the set square, draw an angle of a)45o b)30o c)105o d)15o Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 2 45o 30o 105o 15o Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 3 For each angle below, state whether the angle is acute, obtuse or reflex: Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 3 For each angle below, state whether the angle is acute, obtuse or reflex: Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 4 Measure the following angles: Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 4 Measure the following angles: Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : 2 5o 17 30 : 3 3 hr 14 min 18 sec: 4 15 hr 56 min 24 sec: Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : forty degrees, twenty minutes and fifty seconds. 2 5o 17 30 : five degrees, seventeen minutes and thirty seconds. 3 3 hr 14 min 18 sec: three hours, fourteen minutes and eighteen seconds. 4 15 hr 56 min 24 sec: fifteen hours, fifty-eight minutes and twenty-four seconds. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : forty degrees, twenty minutes and fifty seconds. 2 5o 17 30 : five degrees, seventeen minutes and thirty seconds. 3 3 hr 14 min 18 sec: three hours, fourteen minutes and eighteen seconds. 4 15 hr 56 min 24 sec: fifteen hours, fifty-eight minutes and twenty-four seconds. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : forty degrees, twenty minutes and fifty seconds. 2 5o 17 30 : five degrees, seventeen minutes and thirty seconds. 3 3 hr 14 min 18 sec: three hours, fourteen minutes and eighteen seconds. 4 15 hr 56 min 24 sec: fifteen hours, fifty-eight minutes and twenty-four seconds. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : forty degrees, twenty minutes and fifty seconds. 2 5o 17 30 : five degrees, seventeen minutes and thirty seconds. 3 3 hr 14 min 18 sec: three hours, fourteen minutes and eighteen seconds. 4 15 hr 56 min 24 sec: fifteen hours, fifty-eight minutes and twenty-four seconds. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : forty degrees, twenty minutes and fifty seconds. 2 5o 17 30 : five degrees, seventeen minutes and thirty seconds. 3 3 hr 14 min 18 sec: three hours, fourteen minutes and eighteen seconds. 4 15 hr 56 min 24 sec: fifteen hours, fifty-eight minutes and twenty-four seconds. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 = 2 55o 44 52 + 24o 53 34 = 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec = 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec = Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 =45o 27 30 2 55o 44 52 + 24o 53 34 =80o 38 26 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec =7 hr 45 min 51 sec 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec =1 day 7 hr 1 min 11 sec Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 =45o 27 30 2 55o 44 52 + 24o 53 34 =80o 38 26 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec =7 hr 45 min 51 sec 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec =1 day 7 hr 1 min 11 sec Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 =45o 27 30 2 55o 44 52 + 24o 53 34 =80o 38 26 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec =7 hr 45 min 51 sec 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec =1 day 7 hr 1 min 11 sec Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 =45o 27 30 2 55o 44 52 + 24o 53 34 =80o 38 26 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec =7 hr 45 min 51 sec 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec =1 day 7 hr 1 min 11 sec Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 =45o 27 30 2 55o 44 52 + 24o 53 34 =80o 38 26 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec =7 hr 45 min 51 sec 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec =1 day 7 hr 1 min 11 sec Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 = 2 53o 24 12 − 32o 43 44 = 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec = 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec = Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 =12o 9 30 2 53o 24 12 − 32o 43 44 =20o 40 26 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec =2 hr 23 min 10sec 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec =2 hr 58 min 37sec Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 =12o 9 30 2 53o 24 12 − 32o 43 44 =20o 40 26 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec =2 hr 23 min 10sec 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec =2 hr 58 min 37sec Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 =12o 9 30 2 53o 24 12 − 32o 43 44 =20o 40 26 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec =2 hr 23 min 10sec 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec =2 hr 58 min 37sec Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 =12o 9 30 2 53o 24 12 − 32o 43 44 =20o 40 26 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec =2 hr 23 min 10sec 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec =2 hr 58 min 37sec Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 =12o 9 30 2 53o 24 12 − 32o 43 44 =20o 40 26 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec =2 hr 23 min 10sec 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec =2 hr 58 min 37sec Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 9 Luis is a marathon runner. He trains two days: on the first day he runs the marathon in 2 hr 48 min 35 sec; and on the second day he runs it in 2 hr 45 min 30 sec. How long does Luis run over the two days in total? Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 9 Luis is a marathon runner. He trains two days: on the first day he runs the marathon in 2 hr 48 min 35 sec; and on the second day he runs it in 2 hr 45 min 30 sec. How long does Luis run over the two days in total? Data: First day: 2 hr 48 min 35 sec Second day: 2 hr 45 min 30 sec 2 hr 48 min 35 sec + 2 hr 45 min 30 sec Answer: Luis runs 5 hr 34 min 5 sec 5 hr 34 min 5 sec in total. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 9 Luis is a marathon runner. He trains two days: on the first day he runs the marathon in 2 hr 48 min 35 sec; and on the second day he runs it in 2 hr 45 min 30 sec. How long does Luis run over the two days in total? Data: First day: 2 hr 48 min 35 sec Second day: 2 hr 45 min 30 sec 2 hr 48 min 35 sec + 2 hr 45 min 30 sec Answer: Luis runs 5 hr 34 min 5 sec 5 hr 34 min 5 sec in total. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 9 Luis is a marathon runner. He trains two days: on the first day he runs the marathon in 2 hr 48 min 35 sec; and on the second day he runs it in 2 hr 45 min 30 sec. How long does Luis run over the two days in total? Data: First day: 2 hr 48 min 35 sec Second day: 2 hr 45 min 30 sec 2 hr 48 min 35 sec + 2 hr 45 min 30 sec Answer: Luis runs 5 hr 34 min 5 sec 5 hr 34 min 5 sec in total. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 9 Luis is a marathon runner. He trains two days: on the first day he runs the marathon in 2 hr 48 min 35 sec; and on the second day he runs it in 2 hr 45 min 30 sec. How long does Luis run over the two days in total? Data: First day: 2 hr 48 min 35 sec Second day: 2 hr 45 min 30 sec 2 hr 48 min 35 sec + 2 hr 45 min 30 sec Answer: Luis runs 5 hr 34 min 5 sec 5 hr 34 min 5 sec in total. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 10 Ana spent 7 hr 20 min 28 sec on painting a room in the weekend. She worked the same amount of time each day. How much time did she work each day? Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 10 Ana spent 7 hr 20 min 28 sec on painting a room in the weekend. She worked the same amount of time each day. How much time did she work each day? Data: She Ana spent 7 hr 20 min 28 sec 1 hr 40 min 14 sec + 1 hr 40 min 14 sec Answer: She worked 3 hr 20 min 28 sec 1 hr 40 min 14 sec a day. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 10 Ana spent 7 hr 20 min 28 sec on painting a room in the weekend. She worked the same amount of time each day. How much time did she work each day? Data: She Ana spent 7 hr 20 min 28 sec 1 hr 40 min 14 sec + 1 hr 40 min 14 sec Answer: She worked 3 hr 20 min 28 sec 1 hr 40 min 14 sec a day. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 10 Ana spent 7 hr 20 min 28 sec on painting a room in the weekend. She worked the same amount of time each day. How much time did she work each day? Data: She Ana spent 7 hr 20 min 28 sec 1 hr 40 min 14 sec + 1 hr 40 min 14 sec Answer: She worked 3 hr 20 min 28 sec 1 hr 40 min 14 sec a day. Angles and Lines
Indice Lines Bisectors Sexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 10 Ana spent 7 hr 20 min 28 sec on painting a room in the weekend. She worked the same amount of time each day. How much time did she work each day? Data: She Ana spent 7 hr 20 min 28 sec 1 hr 40 min 14 sec + 1 hr 40 min 14 sec Answer: She worked 3 hr 20 min 28 sec 1 hr 40 min 14 sec a day. Angles and Lines

More Related Content

PPT
Lines line segments rays and angles
bySarawut Charoenrob
 
PPTX
Lines and angles presentation
byAnnmarie1020
 
PDF
Unit9: Angles and Lines
byAlberto Pardo Milanés
 
PPT
Geometry Vocabulary
byisabelri
 
ODP
Planer Geometry Guide
byguest85b701
 
ODP
Planar Geometry Terms
byguest2b18d
 
PPTX
LINES AND ANGLE PPT
byARMAN BENIPAL
 
PPTX
Lines and angles
byVarun Arora
 
Lines line segments rays and angles
bySarawut Charoenrob
 
Lines and angles presentation
byAnnmarie1020
 
Unit9: Angles and Lines
byAlberto Pardo Milanés
 
Geometry Vocabulary
byisabelri
 
Planer Geometry Guide
byguest85b701
 
Planar Geometry Terms
byguest2b18d
 
LINES AND ANGLE PPT
byARMAN BENIPAL
 
Lines and angles
byVarun Arora
 

What's hot

PPTX
Parallel and perpendicular lines
byjennyelsoury
 
PPT
Line powerpoint
bySarawut Charoenrob
 
PPTX
Lines and angles
byKulbir Ghagga
 
PPTX
Lines and Angles
byAgraj Garg
 
PPTX
Lines, Angles and Triangles
byAngel Mae Longakit
 
PPTX
Lines and angles
byGurdeep Cris
 
PPTX
point,line,ray
bymirabubakar1
 
PPTX
Lines and angles
byMohammed Nehan
 
PPTX
lines and angles
byAmarjeet Rai
 
PPTX
Lines and angles
byNAINA
 
PPT
Geometry Guide
byguestac35d61
 
PPTX
Geometry basics better view
byavdheshtripathi2
 
PPTX
Linesandangles 111014002441-phpapp02
byAnshuman Kumar
 
PPTX
Jjj
byRocky Sandeep Srk
 
KEY
Chapter 9 kn - Lines, angles, and polygons
byPhoebe Peng-Nolte
 
PPTX
Lines and line segments
bycmletona
 
PPTX
Solve Lines and Angles Question Paper for CBSE Class 9
bySweetySehrawat
 
PPTX
IX Lines and Angles
byBhawna Khurana
 
PPS
Line And Angle Relationships
bysedanor
 
Parallel and perpendicular lines
byjennyelsoury
 
Line powerpoint
bySarawut Charoenrob
 
Lines and angles
byKulbir Ghagga
 
Lines and Angles
byAgraj Garg
 
Lines, Angles and Triangles
byAngel Mae Longakit
 
Lines and angles
byGurdeep Cris
 
point,line,ray
bymirabubakar1
 
Lines and angles
byMohammed Nehan
 
lines and angles
byAmarjeet Rai
 
Lines and angles
byNAINA
 
Geometry Guide
byguestac35d61
 
Geometry basics better view
byavdheshtripathi2
 
Linesandangles 111014002441-phpapp02
byAnshuman Kumar
 
Jjj
byRocky Sandeep Srk
 
Chapter 9 kn - Lines, angles, and polygons
byPhoebe Peng-Nolte
 
Lines and line segments
bycmletona
 
Solve Lines and Angles Question Paper for CBSE Class 9
bySweetySehrawat
 
IX Lines and Angles
byBhawna Khurana
 
Line And Angle Relationships
bysedanor
 

Viewers also liked

PPT
Biodiesel
byNaveen Sihag
 
PDF
20120922 social media tips & trics voor mycoachday lovendegem
byTrigger.social - social media marketing & training
 
PPT
3 d tv
byNaveen Sihag
 
PDF
tepsi-completo
byNatalia Maffeis
 
PDF
20120927 voordracht bij marnixring waregem
byTrigger.social - social media marketing & training
 
PDF
Unit1
byAlberto Pardo Milanés
 
PDF
Decimals
byAlberto Pardo Milanés
 
PDF
social media & HR: voordracht voor Hudson Belgium
byTrigger.social - social media marketing & training
 
PPTX
A 12
byNaveen Sihag
 
PPT
Fuel cells
byNaveen Sihag
 
PDF
Bryochette jonge ondernemers
byTrigger.social - social media marketing & training
 
PPT
Apple i phone
byNaveen Sihag
 
PDF
Portfolio
bydawnbrink
 
PDF
Counting Numbers
byAlberto Pardo Milanés
 
PDF
Factors and multiples
byAlberto Pardo Milanés
 
PDF
Poetry3
byihatebunniesmore
 
PPTX
Nokia
byNaveen Sihag
 
PPT
Database
byNaveen Sihag
 
PPT
3 g
byNaveen Sihag
 
PDF
Workshop linkedin
byTrigger.social - social media marketing & training
 
Biodiesel
byNaveen Sihag
 
20120922 social media tips & trics voor mycoachday lovendegem
byTrigger.social - social media marketing & training
 
3 d tv
byNaveen Sihag
 
tepsi-completo
byNatalia Maffeis
 
20120927 voordracht bij marnixring waregem
byTrigger.social - social media marketing & training
 
Unit1
byAlberto Pardo Milanés
 
Decimals
byAlberto Pardo Milanés
 
social media & HR: voordracht voor Hudson Belgium
byTrigger.social - social media marketing & training
 
A 12
byNaveen Sihag
 
Fuel cells
byNaveen Sihag
 
Bryochette jonge ondernemers
byTrigger.social - social media marketing & training
 
Apple i phone
byNaveen Sihag
 
Portfolio
bydawnbrink
 
Counting Numbers
byAlberto Pardo Milanés
 
Factors and multiples
byAlberto Pardo Milanés
 
Poetry3
byihatebunniesmore
 
Nokia
byNaveen Sihag
 
Database
byNaveen Sihag
 
3 g
byNaveen Sihag
 
Workshop linkedin
byTrigger.social - social media marketing & training
 

Similar to Unit9

PDF
1 ESO - UNIT 10 - LINES AND ANGLES. GEOMETRIC FIGURES.
byGogely The Great
 
PPTX
Line_and_angles_chap_2.pptx ppt ppt ppt ppt
bysushantsambrekar06
 
KEY
Integrated Math 2 Section 5-2
byJimbo Lamb
 
KEY
Int Math 2 Section 5-2 1011
byJimbo Lamb
 
PPT
Geometry
byAzrul Fazwan
 
ODP
Mat_5th_UD3_Angles
byTRMaria
 
PPT
Pre geometry
bymstf mstf
 
PPTX
ANALYTIC-GEOMETRY(4).pptx
byBercasioKelvin
 
PPTX
Geometry
byKatina1196
 
PPTX
Trigo Lecture 2.pptx
byMathithiasIIAviles
 
DOC
Definitions
byJanet Hanshaw
 
PPTX
Addition-and-Subtraction-of-Fractions-Mathematics-Presentation-in-Blue-Green-...
byjamesboloron1006
 
PDF
Trig m1 handouts
byguevarra_2000
 
PPTX
t1 angles and trigonometric functions
bymath260
 
PPT
Sat index cards
bytschmucker
 
PDF
Sexagesimal system
byAlberto Pardo Milanés
 
PPT
Trignometryppt
byAnand Yadav
 
PPTX
Lines n angles
byPunita Verma
 
PDF
subject-maths ,chapter- line and angle, class-9
byaditya941125
 
PPTX
Angles properties mathematics solutions by dr. otundo martin
byMartin Otundo
 
1 ESO - UNIT 10 - LINES AND ANGLES. GEOMETRIC FIGURES.
byGogely The Great
 
Line_and_angles_chap_2.pptx ppt ppt ppt ppt
bysushantsambrekar06
 
Integrated Math 2 Section 5-2
byJimbo Lamb
 
Int Math 2 Section 5-2 1011
byJimbo Lamb
 
Geometry
byAzrul Fazwan
 
Mat_5th_UD3_Angles
byTRMaria
 
Pre geometry
bymstf mstf
 
ANALYTIC-GEOMETRY(4).pptx
byBercasioKelvin
 
Geometry
byKatina1196
 
Trigo Lecture 2.pptx
byMathithiasIIAviles
 
Definitions
byJanet Hanshaw
 
Addition-and-Subtraction-of-Fractions-Mathematics-Presentation-in-Blue-Green-...
byjamesboloron1006
 
Trig m1 handouts
byguevarra_2000
 
t1 angles and trigonometric functions
bymath260
 
Sat index cards
bytschmucker
 
Sexagesimal system
byAlberto Pardo Milanés
 
Trignometryppt
byAnand Yadav
 
Lines n angles
byPunita Verma
 
subject-maths ,chapter- line and angle, class-9
byaditya941125
 
Angles properties mathematics solutions by dr. otundo martin
byMartin Otundo
 

More from Alberto Pardo Milanés

PPTX
La francophonie
byAlberto Pardo Milanés
 
PDF
Algebraic expressions
byAlberto Pardo Milanés
 
PDF
Proportions and percentages
byAlberto Pardo Milanés
 
PDF
Decimals
byAlberto Pardo Milanés
 
PDF
Handling data and probability
byAlberto Pardo Milanés
 
PDF
Fractions
byAlberto Pardo Milanés
 
PDF
Fractions and multiples
byAlberto Pardo Milanés
 
PDF
Integers
byAlberto Pardo Milanés
 
PDF
The Race, INTEGERS MATHS GAME
byAlberto Pardo Milanés
 
PDF
Unit00
byAlberto Pardo Milanés
 
PDF
Unit11
byAlberto Pardo Milanés
 
PDF
Unit12
byAlberto Pardo Milanés
 
PDF
Origami triangles
byAlberto Pardo Milanés
 
PDF
Hexagon
byAlberto Pardo Milanés
 
PDF
Equilateraltriangle
byAlberto Pardo Milanés
 
PDF
Pentagon
byAlberto Pardo Milanés
 
PDF
Unit6: Algebraic expressions and equations
byAlberto Pardo Milanés
 
PDF
Unit5
byAlberto Pardo Milanés
 
PDF
Unit4
byAlberto Pardo Milanés
 
PDF
Unit2
byAlberto Pardo Milanés
 
La francophonie
byAlberto Pardo Milanés
 
Algebraic expressions
byAlberto Pardo Milanés
 
Proportions and percentages
byAlberto Pardo Milanés
 
Decimals
byAlberto Pardo Milanés
 
Handling data and probability
byAlberto Pardo Milanés
 
Fractions
byAlberto Pardo Milanés
 
Fractions and multiples
byAlberto Pardo Milanés
 
Integers
byAlberto Pardo Milanés
 
The Race, INTEGERS MATHS GAME
byAlberto Pardo Milanés
 
Unit00
byAlberto Pardo Milanés
 
Unit11
byAlberto Pardo Milanés
 
Unit12
byAlberto Pardo Milanés
 
Origami triangles
byAlberto Pardo Milanés
 
Hexagon
byAlberto Pardo Milanés
 
Equilateraltriangle
byAlberto Pardo Milanés
 
Pentagon
byAlberto Pardo Milanés
 
Unit6: Algebraic expressions and equations
byAlberto Pardo Milanés
 
Unit5
byAlberto Pardo Milanés
 
Unit4
byAlberto Pardo Milanés
 
Unit2
byAlberto Pardo Milanés
 

Recently uploaded

PPTX
Greengnorance Toolkit Module 4 Active Mobility and Transport
byKarl Donert
 
PPTX
Greengnorance Toolkit Module1 Climate Change
byKarl Donert
 
PDF
Workshop 29 Crystal Review All Students by YogiGoddess
by©LDMMIA, ©Reiki Yoga
 
PDF
Power, Propaganda, and Fear: A Study of W. H. Auden’s Epitaph on a Tyrant
bypriyarathod315
 
PDF
Chapter 05 Drugs Acting on the Central Nervous System: Anticonvulsant (Antiep...
bySandeshSul
 
PPTX
WEEK 2 (2).pptx TLE COOKERY 10 QUARTER 4
byResynFayeCortez2
 
PDF
Four Stars Of Destiny By General Manoj Mukund Naravane
byAman744562
 
PPTX
How to Create_Generate Engineering Change Orders ECOs in Odoo 18
byCeline George
 
PDF
"Perfection of a Kind": A New Critical Reading of W.H. Auden’s Epitaph on a T...
byKruti Vyas
 
PDF
AI Is a Tool, Not a Voice: Radio, Trust, and the Human Factor
byN.A. Shah Ansari
 
PDF
Pharmaceutical Quality Assurance Unit 1 (BP606T)
byChetan Mali
 
PPTX
Renal Physiology- Juxtaglomerular Apparatus.pptx
byDisha Soriya
 
PPTX
Problem and Solution (PowerPoint Game Template)
byacpaulite
 
PDF
"September 1, 1939": A Modern Reading of Auden in Times of Crisis
byKruti Vyas
 
PDF
A Study of W. H. Auden’s September 1, 1939
bypriyarathod315
 
PDF
Family and Marriage __ Sociology __ Jhasketan Kuanar __ NURSING VIBE ONLY .pdf
byJK NURSING VIBES ONLY JHASKETAN KUANAR
 
PDF
The Sheep and the Goat: Beckett’s Subversion of Divine Justice in Waiting for...
bysejadchokiya
 
PDF
How "Raiders of the Lost Ark" and "Ordinary People" Employ Non-Verbal Acting
by6x5csns4pn
 
PPTX
Greengnorance Toolkit Module 6 Water Resources
byKarl Donert
 
PPTX
Greengnorance Toolkit Module 5 Waste Management
byKarl Donert
 
Greengnorance Toolkit Module 4 Active Mobility and Transport
byKarl Donert
 
Greengnorance Toolkit Module1 Climate Change
byKarl Donert
 
Workshop 29 Crystal Review All Students by YogiGoddess
by©LDMMIA, ©Reiki Yoga
 
Power, Propaganda, and Fear: A Study of W. H. Auden’s Epitaph on a Tyrant
bypriyarathod315
 
Chapter 05 Drugs Acting on the Central Nervous System: Anticonvulsant (Antiep...
bySandeshSul
 
WEEK 2 (2).pptx TLE COOKERY 10 QUARTER 4
byResynFayeCortez2
 
Four Stars Of Destiny By General Manoj Mukund Naravane
byAman744562
 
How to Create_Generate Engineering Change Orders ECOs in Odoo 18
byCeline George
 
"Perfection of a Kind": A New Critical Reading of W.H. Auden’s Epitaph on a T...
byKruti Vyas
 
AI Is a Tool, Not a Voice: Radio, Trust, and the Human Factor
byN.A. Shah Ansari
 
Pharmaceutical Quality Assurance Unit 1 (BP606T)
byChetan Mali
 
Renal Physiology- Juxtaglomerular Apparatus.pptx
byDisha Soriya
 
Problem and Solution (PowerPoint Game Template)
byacpaulite
 
"September 1, 1939": A Modern Reading of Auden in Times of Crisis
byKruti Vyas
 
A Study of W. H. Auden’s September 1, 1939
bypriyarathod315
 
Family and Marriage __ Sociology __ Jhasketan Kuanar __ NURSING VIBE ONLY .pdf
byJK NURSING VIBES ONLY JHASKETAN KUANAR
 
The Sheep and the Goat: Beckett’s Subversion of Divine Justice in Waiting for...
bysejadchokiya
 
How "Raiders of the Lost Ark" and "Ordinary People" Employ Non-Verbal Acting
by6x5csns4pn
 
Greengnorance Toolkit Module 6 Water Resources
byKarl Donert
 
Greengnorance Toolkit Module 5 Waste Management
byKarl Donert
 

Unit9

  • 1.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Angles and Lines Matem´ticas 1o E.S.O. a -
  • 2.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises 1 Lines 2 Perpendicular bisector of a segment and bisector of an angle 3 Sexagesimal system and angles 4 Sexagesimal system and time 5 Adding and Subtracting in the sexagesimal system 6 Exercises Angles and Lines
  • 3.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Lines Angles and Lines
  • 4.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Lines Plane Geometry Plane Geometry deals with figures in a plane (circles, lines, polygons. . . ) A line is a set of points extending in two opposite directions without end, It’s a straight one-dimensional figure with no thickness and extending infinitely in both directions. A line is sometimes called a straight line. Points are said to be collinear points if they lie on a single straight line. A plane is a flat surface that has no thickness and extends without ending in ALL directions. Points are said to be coplanar points if they lie on a common plane. A line segment is a finite portion of an infinite line. A line segment always has a beginning and an end. Angles and Lines
  • 5.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Lines Plane Geometry Plane Geometry deals with figures in a plane (circles, lines, polygons. . . ) A line is a set of points extending in two opposite directions without end, It’s a straight one-dimensional figure with no thickness and extending infinitely in both directions. A line is sometimes called a straight line. Points are said to be collinear points if they lie on a single straight line. A plane is a flat surface that has no thickness and extends without ending in ALL directions. Points are said to be coplanar points if they lie on a common plane. A line segment is a finite portion of an infinite line. A line segment always has a beginning and an end. Angles and Lines
  • 6.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Lines Perpendicular bisector of a segment and bisector of an angle Lines that intersect in a point are called intersecting lines. Lines that do not intersect are called parallel lines (in the plane). Two lines that lie on top of one another are called coincident lines. Two lines or line segments which are perpendicular are said to be orthogonal (two lines are said to be perpendicular if they meet at a 90o angle). Given two intersecting lines, the point of intersection is called the vertex and the amount of rotation about the vertex required to bring one line into correspondence with the other is called the angle between them. Angles and Lines
  • 7.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Lines One full rotation corresponds to 360 degrees. Half a full rotation is called a straight angle, and a quarter of a full rotation is called a right angle. An angle less than a right angle is called an acute angle, an angle greater than a right angle (but less than a straight angle) is called an obtuse angle, and an angle greater than a straight angle (but less than a full angle) is called a reflex angle. Angles and Lines
  • 8.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Perpendicular bisector of a segment and bisector of an angle Angles and Lines
  • 9.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Perpendicular bisector of a segment and bisector of an angle Bisector of a line segment A perpendicular bisector of a line segment AB is a line perpendicular to AB and passing through the midpoint M of AB. Angles and Lines
  • 10.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Perpendicular bisector of a segment and bisector of an angle Bisector of an angle The bisector of an angle is the line that divides the angle into two equal parts. Angles and Lines
  • 11.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and angles Angles and Lines
  • 12.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and angles The size of an angle There are several ways to measure the size of an angle, for example using units of degrees: In a complete circle there are three hundred and sixty degrees. You can express angles to any precision using decimal numbers. Example: 30 degrees and a half is 30.5 degrees. There is another way to state the size of an angle, subdividing a degree. The degree is divided into sixty parts called minutes. These minutes are further divided into sixty parts called seconds. Angles and Lines
  • 13.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and angles The size of an angle There are several ways to measure the size of an angle, for example using units of degrees: In a complete circle there are three hundred and sixty degrees. You can express angles to any precision using decimal numbers. Example: 30 degrees and a half is 30.5 degrees. There is another way to state the size of an angle, subdividing a degree. The degree is divided into sixty parts called minutes. These minutes are further divided into sixty parts called seconds. Angles and Lines
  • 14.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and angles Angles: Degrees, minutes and seconds In a full circle there are 360 degrees, each degree is split up into 60 parts called minutes (each part being 1/60 of a degree), each minute is split up into 60 parts called seconds (each part being 1/60 of a minute). Example: 40 degrees, 20 minutes and 50 seconds is usually written this way: 40o 20 50 . Example: 30.5 degrees is 30o and 30 , because 0.5 degrees are 0.5 · 60 = 30 minutes. Angles and Lines
  • 15.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and angles Angles: Degrees, minutes and seconds In a full circle there are 360 degrees, each degree is split up into 60 parts called minutes (each part being 1/60 of a degree), each minute is split up into 60 parts called seconds (each part being 1/60 of a minute). Example: 40 degrees, 20 minutes and 50 seconds is usually written this way: 40o 20 50 . Example: 30.5 degrees is 30o and 30 , because 0.5 degrees are 0.5 · 60 = 30 minutes. Angles and Lines
  • 16.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and time Angles and Lines
  • 17.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and time Time: Hours, minutes and seconds To measure time we can use hours: In a day there are twenty-four hours. You can express time to any precision using decimal numbers. Example: 3 hours and a quarter is 3.25 hours. There is another way to state the amount of time, subdividing an hour. The hour is divided into sixty parts called minutes. These minutes are further divided into sixty parts called seconds. In a day there are 24 hours, each hour is split up into 60 parts called minutes (each part being 1/60 of an hour), each minute is split up into 60 parts called seconds (each part being 1/60 of a minute). Example: 14 hours, 56 minutes and 12 seconds is usually written this way: 14 hr 56 min 12 sec. Example: 3.25 hours is 3 hr and 15 min, because 0.25 hours are 0.25 · 60 = 15 minutes. Angles and Lines
  • 18.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and time Time: Hours, minutes and seconds To measure time we can use hours: In a day there are twenty-four hours. You can express time to any precision using decimal numbers. Example: 3 hours and a quarter is 3.25 hours. There is another way to state the amount of time, subdividing an hour. The hour is divided into sixty parts called minutes. These minutes are further divided into sixty parts called seconds. In a day there are 24 hours, each hour is split up into 60 parts called minutes (each part being 1/60 of an hour), each minute is split up into 60 parts called seconds (each part being 1/60 of a minute). Example: 14 hours, 56 minutes and 12 seconds is usually written this way: 14 hr 56 min 12 sec. Example: 3.25 hours is 3 hr and 15 min, because 0.25 hours are 0.25 · 60 = 15 minutes. Angles and Lines
  • 19.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Sexagesimal system and time Time: Hours, minutes and seconds To measure time we can use hours: In a day there are twenty-four hours. You can express time to any precision using decimal numbers. Example: 3 hours and a quarter is 3.25 hours. There is another way to state the amount of time, subdividing an hour. The hour is divided into sixty parts called minutes. These minutes are further divided into sixty parts called seconds. In a day there are 24 hours, each hour is split up into 60 parts called minutes (each part being 1/60 of an hour), each minute is split up into 60 parts called seconds (each part being 1/60 of a minute). Example: 14 hours, 56 minutes and 12 seconds is usually written this way: 14 hr 56 min 12 sec. Example: 3.25 hours is 3 hr and 15 min, because 0.25 hours are 0.25 · 60 = 15 minutes. Angles and Lines
  • 20.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Angles and Lines
  • 21.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Add in the sexagesimal system You must add or subtract the units separately. But you may need to do some adjusting if the hours end up 24 or more, the minutes end up 60 or more, the seconds end up 60 or more,or less than zero. Adding Add the hours. If the hours are 24 or more, subtract 24 from the hours and add 1 to the days. Add the minutes. If the minutes are 60 or more, subtract 60 from the hours and add 1 to the hours. And so on. Example: 40o 20 50 + 10o 33 6 = 50o 55 56 . Example: 14 hr 20 min 50 sec + 15 hr 43 min 26 sec =29 hr 63 min 76 sec =1 day 6 hr 4 min 16 sec. Angles and Lines
  • 22.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Add in the sexagesimal system You must add or subtract the units separately. But you may need to do some adjusting if the hours end up 24 or more, the minutes end up 60 or more, the seconds end up 60 or more,or less than zero. Adding Add the hours. If the hours are 24 or more, subtract 24 from the hours and add 1 to the days. Add the minutes. If the minutes are 60 or more, subtract 60 from the hours and add 1 to the hours. And so on. Example: 40o 20 50 + 10o 33 6 = 50o 55 56 . Example: 14 hr 20 min 50 sec + 15 hr 43 min 26 sec =29 hr 63 min 76 sec =1 day 6 hr 4 min 16 sec. Angles and Lines
  • 23.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Add in the sexagesimal system You must add or subtract the units separately. But you may need to do some adjusting if the hours end up 24 or more, the minutes end up 60 or more, the seconds end up 60 or more,or less than zero. Adding Add the hours. If the hours are 24 or more, subtract 24 from the hours and add 1 to the days. Add the minutes. If the minutes are 60 or more, subtract 60 from the hours and add 1 to the hours. And so on. Example: 40o 20 50 + 10o 33 6 = 50o 55 56 . Example: 14 hr 20 min 50 sec + 15 hr 43 min 26 sec =29 hr 63 min 76 sec =1 day 6 hr 4 min 16 sec. Angles and Lines
  • 24.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Add in the sexagesimal system You must add or subtract the units separately. But you may need to do some adjusting if the hours end up 24 or more, the minutes end up 60 or more, the seconds end up 60 or more,or less than zero. Adding Add the hours. If the hours are 24 or more, subtract 24 from the hours and add 1 to the days. Add the minutes. If the minutes are 60 or more, subtract 60 from the hours and add 1 to the hours. And so on. Example: 40o 20 50 + 10o 33 6 = 50o 55 56 . Example: 14 hr 20 min 50 sec + 15 hr 43 min 26 sec =29 hr 63 min 76 sec =1 day 6 hr 4 min 16 sec. Angles and Lines
  • 25.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Subtract in the sexagesimal system Subtracting Subtract the hours. If the hours are negative, add 24 to the hours and subtract 1 from days. Subtract the minutes. If the minutes are negative, add 60 to the minutes and subtract 1 from hours. And so on. Example: 23 hr 40 min 51 sec − 15 hr 33 min 21 sec = 8 hr 7 min 30 sec. Example: 45o 33 12 −11o 42 20 =44o 92 72 −11o 42 20 =33o 50 52 . Angles and Lines
  • 26.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Subtract in the sexagesimal system Subtracting Subtract the hours. If the hours are negative, add 24 to the hours and subtract 1 from days. Subtract the minutes. If the minutes are negative, add 60 to the minutes and subtract 1 from hours. And so on. Example: 23 hr 40 min 51 sec − 15 hr 33 min 21 sec = 8 hr 7 min 30 sec. Example: 45o 33 12 −11o 42 20 =44o 92 72 −11o 42 20 =33o 50 52 . Angles and Lines
  • 27.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Subtract in the sexagesimal system Subtracting Subtract the hours. If the hours are negative, add 24 to the hours and subtract 1 from days. Subtract the minutes. If the minutes are negative, add 60 to the minutes and subtract 1 from hours. And so on. Example: 23 hr 40 min 51 sec − 15 hr 33 min 21 sec = 8 hr 7 min 30 sec. Example: 45o 33 12 −11o 42 20 =44o 92 72 −11o 42 20 =33o 50 52 . Angles and Lines
  • 28.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Subtract in the sexagesimal system Subtracting Subtract the hours. If the hours are negative, add 24 to the hours and subtract 1 from days. Subtract the minutes. If the minutes are negative, add 60 to the minutes and subtract 1 from hours. And so on. Example: 23 hr 40 min 51 sec − 15 hr 33 min 21 sec = 8 hr 7 min 30 sec. Example: 45o 33 12 −11o 42 20 =44o 92 72 −11o 42 20 =33o 50 52 . Angles and Lines
  • 29.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Adding and Subtracting in the sexagesimal system Subtract in the sexagesimal system Subtracting Subtract the hours. If the hours are negative, add 24 to the hours and subtract 1 from days. Subtract the minutes. If the minutes are negative, add 60 to the minutes and subtract 1 from hours. And so on. Example: 23 hr 40 min 51 sec − 15 hr 33 min 21 sec = 8 hr 7 min 30 sec. Example: 45o 33 12 −11o 42 20 =44o 92 72 −11o 42 20 =33o 50 52 . Angles and Lines
  • 30.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Angles and Lines
  • 31.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 1 Find five objects in your classroom that have right angles: Angles and Lines
  • 32.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 1 Find five objects in your classroom that have right angles: Angles and Lines
  • 33.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 2 Using the set square, draw an angle of a)45o b)30o c)105o d)15o Angles and Lines
  • 34.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 2 45o 30o 105o 15o Angles and Lines
  • 35.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 3 For each angle below, state whether the angle is acute, obtuse or reflex: Angles and Lines
  • 36.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 3 For each angle below, state whether the angle is acute, obtuse or reflex: Angles and Lines
  • 37.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 4 Measure the following angles: Angles and Lines
  • 38.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 4 Measure the following angles: Angles and Lines
  • 39.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : 2 5o 17 30 : 3 3 hr 14 min 18 sec: 4 15 hr 56 min 24 sec: Angles and Lines
  • 40.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : forty degrees, twenty minutes and fifty seconds. 2 5o 17 30 : five degrees, seventeen minutes and thirty seconds. 3 3 hr 14 min 18 sec: three hours, fourteen minutes and eighteen seconds. 4 15 hr 56 min 24 sec: fifteen hours, fifty-eight minutes and twenty-four seconds. Angles and Lines
  • 41.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : forty degrees, twenty minutes and fifty seconds. 2 5o 17 30 : five degrees, seventeen minutes and thirty seconds. 3 3 hr 14 min 18 sec: three hours, fourteen minutes and eighteen seconds. 4 15 hr 56 min 24 sec: fifteen hours, fifty-eight minutes and twenty-four seconds. Angles and Lines
  • 42.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : forty degrees, twenty minutes and fifty seconds. 2 5o 17 30 : five degrees, seventeen minutes and thirty seconds. 3 3 hr 14 min 18 sec: three hours, fourteen minutes and eighteen seconds. 4 15 hr 56 min 24 sec: fifteen hours, fifty-eight minutes and twenty-four seconds. Angles and Lines
  • 43.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : forty degrees, twenty minutes and fifty seconds. 2 5o 17 30 : five degrees, seventeen minutes and thirty seconds. 3 3 hr 14 min 18 sec: three hours, fourteen minutes and eighteen seconds. 4 15 hr 56 min 24 sec: fifteen hours, fifty-eight minutes and twenty-four seconds. Angles and Lines
  • 44.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 6 Write down the following amounts: 1 43o 34 25 : forty degrees, twenty minutes and fifty seconds. 2 5o 17 30 : five degrees, seventeen minutes and thirty seconds. 3 3 hr 14 min 18 sec: three hours, fourteen minutes and eighteen seconds. 4 15 hr 56 min 24 sec: fifteen hours, fifty-eight minutes and twenty-four seconds. Angles and Lines
  • 45.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 = 2 55o 44 52 + 24o 53 34 = 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec = 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec = Angles and Lines
  • 46.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 =45o 27 30 2 55o 44 52 + 24o 53 34 =80o 38 26 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec =7 hr 45 min 51 sec 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec =1 day 7 hr 1 min 11 sec Angles and Lines
  • 47.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 =45o 27 30 2 55o 44 52 + 24o 53 34 =80o 38 26 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec =7 hr 45 min 51 sec 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec =1 day 7 hr 1 min 11 sec Angles and Lines
  • 48.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 =45o 27 30 2 55o 44 52 + 24o 53 34 =80o 38 26 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec =7 hr 45 min 51 sec 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec =1 day 7 hr 1 min 11 sec Angles and Lines
  • 49.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 =45o 27 30 2 55o 44 52 + 24o 53 34 =80o 38 26 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec =7 hr 45 min 51 sec 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec =1 day 7 hr 1 min 11 sec Angles and Lines
  • 50.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 7 Find: 1 34o 14 15 + 11o 13 15 =45o 27 30 2 55o 44 52 + 24o 53 34 =80o 38 26 3 3 hr 34 min 17 sec + 4 hr 11 min 34 sec =7 hr 45 min 51 sec 4 18 hr 34 min 37 sec + 12 hr 26 min 34 sec =1 day 7 hr 1 min 11 sec Angles and Lines
  • 51.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 = 2 53o 24 12 − 32o 43 44 = 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec = 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec = Angles and Lines
  • 52.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 =12o 9 30 2 53o 24 12 − 32o 43 44 =20o 40 26 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec =2 hr 23 min 10sec 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec =2 hr 58 min 37sec Angles and Lines
  • 53.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 =12o 9 30 2 53o 24 12 − 32o 43 44 =20o 40 26 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec =2 hr 23 min 10sec 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec =2 hr 58 min 37sec Angles and Lines
  • 54.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 =12o 9 30 2 53o 24 12 − 32o 43 44 =20o 40 26 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec =2 hr 23 min 10sec 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec =2 hr 58 min 37sec Angles and Lines
  • 55.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 =12o 9 30 2 53o 24 12 − 32o 43 44 =20o 40 26 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec =2 hr 23 min 10sec 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec =2 hr 58 min 37sec Angles and Lines
  • 56.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 8 Find: 1 45o 21 45 − 33o 12 15 =12o 9 30 2 53o 24 12 − 32o 43 44 =20o 40 26 3 6 hr 24 min 15 sec − 4 hr 1 min 5 sec =2 hr 23 min 10sec 4 8 hr 24 min 13 sec − 5 hr 25 min 36 sec =2 hr 58 min 37sec Angles and Lines
  • 57.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 9 Luis is a marathon runner. He trains two days: on the first day he runs the marathon in 2 hr 48 min 35 sec; and on the second day he runs it in 2 hr 45 min 30 sec. How long does Luis run over the two days in total? Angles and Lines
  • 58.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 9 Luis is a marathon runner. He trains two days: on the first day he runs the marathon in 2 hr 48 min 35 sec; and on the second day he runs it in 2 hr 45 min 30 sec. How long does Luis run over the two days in total? Data: First day: 2 hr 48 min 35 sec Second day: 2 hr 45 min 30 sec 2 hr 48 min 35 sec + 2 hr 45 min 30 sec Answer: Luis runs 5 hr 34 min 5 sec 5 hr 34 min 5 sec in total. Angles and Lines
  • 59.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 9 Luis is a marathon runner. He trains two days: on the first day he runs the marathon in 2 hr 48 min 35 sec; and on the second day he runs it in 2 hr 45 min 30 sec. How long does Luis run over the two days in total? Data: First day: 2 hr 48 min 35 sec Second day: 2 hr 45 min 30 sec 2 hr 48 min 35 sec + 2 hr 45 min 30 sec Answer: Luis runs 5 hr 34 min 5 sec 5 hr 34 min 5 sec in total. Angles and Lines
  • 60.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 9 Luis is a marathon runner. He trains two days: on the first day he runs the marathon in 2 hr 48 min 35 sec; and on the second day he runs it in 2 hr 45 min 30 sec. How long does Luis run over the two days in total? Data: First day: 2 hr 48 min 35 sec Second day: 2 hr 45 min 30 sec 2 hr 48 min 35 sec + 2 hr 45 min 30 sec Answer: Luis runs 5 hr 34 min 5 sec 5 hr 34 min 5 sec in total. Angles and Lines
  • 61.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 9 Luis is a marathon runner. He trains two days: on the first day he runs the marathon in 2 hr 48 min 35 sec; and on the second day he runs it in 2 hr 45 min 30 sec. How long does Luis run over the two days in total? Data: First day: 2 hr 48 min 35 sec Second day: 2 hr 45 min 30 sec 2 hr 48 min 35 sec + 2 hr 45 min 30 sec Answer: Luis runs 5 hr 34 min 5 sec 5 hr 34 min 5 sec in total. Angles and Lines
  • 62.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 10 Ana spent 7 hr 20 min 28 sec on painting a room in the weekend. She worked the same amount of time each day. How much time did she work each day? Angles and Lines
  • 63.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 10 Ana spent 7 hr 20 min 28 sec on painting a room in the weekend. She worked the same amount of time each day. How much time did she work each day? Data: She Ana spent 7 hr 20 min 28 sec 1 hr 40 min 14 sec + 1 hr 40 min 14 sec Answer: She worked 3 hr 20 min 28 sec 1 hr 40 min 14 sec a day. Angles and Lines
  • 64.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 10 Ana spent 7 hr 20 min 28 sec on painting a room in the weekend. She worked the same amount of time each day. How much time did she work each day? Data: She Ana spent 7 hr 20 min 28 sec 1 hr 40 min 14 sec + 1 hr 40 min 14 sec Answer: She worked 3 hr 20 min 28 sec 1 hr 40 min 14 sec a day. Angles and Lines
  • 65.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 10 Ana spent 7 hr 20 min 28 sec on painting a room in the weekend. She worked the same amount of time each day. How much time did she work each day? Data: She Ana spent 7 hr 20 min 28 sec 1 hr 40 min 14 sec + 1 hr 40 min 14 sec Answer: She worked 3 hr 20 min 28 sec 1 hr 40 min 14 sec a day. Angles and Lines
  • 66.
    Indice Lines BisectorsSexagesimal system and angles Sexagesimal system and time Adding and Subtracting Exercises Exercises Exercise 10 Ana spent 7 hr 20 min 28 sec on painting a room in the weekend. She worked the same amount of time each day. How much time did she work each day? Data: She Ana spent 7 hr 20 min 28 sec 1 hr 40 min 14 sec + 1 hr 40 min 14 sec Answer: She worked 3 hr 20 min 28 sec 1 hr 40 min 14 sec a day. Angles and Lines