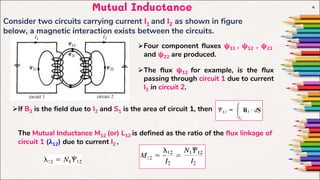
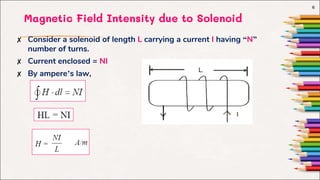
This document discusses inductance and inductors. It defines inductance as the ratio of magnetic flux linkage to current through an inductor. Typical inductors include solenoids, toroids, and coaxial cables. The document then provides formulas for calculating the inductance of these different types of inductors based on their geometry and number of turns. It also defines mutual inductance as the magnetic flux linkage in one circuit due to current in another circuit.

1. UNIT III - MAGNETOSTATICS
Dr.K.G.SHANTHI
Professor/ECE
shanthiece@rmkcet.ac.in
Inductance, Mutual inductance,
Inductance of solenoid, Toroid
and Coaxial cable

2. ✘ A circuit (or closed conducting path) carrying current I produces a
magnetic field B which causes a flux ϕ or ψ to pass through each turn
of the circuit.
✘ If the circuit has N identical turns, we define
the flux linkage λ as
✘ Also, if the medium surrounding the circuit is linear,
the flux linkage λ is proportional to the current I
producing it.
where L is a constant of proportionality called the inductance of the
circuit.
✘ The inductance L is a property of the physical arrangement of the circuit. A circuit or
part of a circuit that has inductance is called an inductor.
✘ Typical examples of inductors are toroids, solenoids, coaxial transmission lines, and
parallel-wire transmission lines.
2
λα I λ= LI
INDUCTANCE AND INDUCTORS
(or)

3. 3
INDUCTANCE AND INDUCTORS
Inductance L of an inductor as the ratio of the magnetic flux linkage λ
to the current I through the inductor; that is,
The unit of inductance is the Henry (H) which is the same as webers/ampere.
The inductance defined by above equation is commonly referred to as
Self Inductance since the linkages are produced by the inductor itself.
 Inductance is a measure of how much magnetic energy is stored in an inductor.
 The magnetic energy (in joules) stored in an inductor is expressed in circuit
theory as:
Thus the self-inductance of a circuit may be defined or calculated from energy
considerations.

4. Mutual Inductance 4
Consider two circuits carrying current I1 and I2 as shown in figure
below, a magnetic interaction exists between the circuits.
Four component fluxes ψ11 , ψ12 , ψ21
and ψ22 are produced.
The flux ψ12 for example, is the flux
passing through circuit 1 due to current
I2 in circuit 2.
If B2 is the field due to I2 and S1 is the area of circuit 1, then
The Mutual Inductance M12 (or) L12 is defined as the ratio of the flux linkage of
circuit 1 (λ12) due to current I2 ,

5. 5
The Mutual Inductance M21 (or) L21 is defined as the ratio of the
flux linkage of circuit 2 (λ21) due to current I1 ,
Mutual Inductance
The Mutual Inductance between two circuits is then the magnetic flux
linkage with one circuit per unit current in the other.
If the medium surrounding the circuits is linear

6. Magnetic Field Intensity due to Solenoid
✘ Consider a solenoid of length L carrying a current I having “N”
number of turns.
✘ Current enclosed = NI
✘ By ampere’s law,
6

7. Inductance of a Solenoid
✘ In case of solenoid of length l and with N turns, the magnetic flux density is
given by,
B = (µo N I/l) -----------------------(1)
✘ The total flux is obtained by multiplying equation (1) by the cross-sectional area
A of the solenoid.
Total flux (φ) = B A= (µo NI/l)A -----------------------(2)
✘ Total flux linkage = Nφ
✘ Total flux linkage = N (µo NI/l)A =µo N2IA/l---------------------(3)
✘ Inductance ‘L’ of the solenoid = Total flux linkage / Total current
✘ L= (µo N2IA)/l I
L= (µo N2A)/l Henry ----------------------(4)
7

8. ✘ Consider a toroidal coil carrying a current I
with mean radius of rm.
✘ Let the number of turns be N.
✘ Current enclosed = NI
✘ By ampere’s law,
8
Magnetic Field Intensity due to a Toroid

9. ✘ Consider a toroid coil with N turns. Let I be the current passing
through this coil and rm be the mean radius of toroid The equation
for magnetic flux density for toroid is,
B = (µo NI)/2πrm
✘ The total flux is, φ = BA= µo NIA/2πrm
✘ The flux linkage = Nφ = µo N2IA/2πrm
✘ The inductance L is the flux linkage divided by the total current I.
L = Nφ /I= µo N2IA/I2πrm = µo N2A/2πrm Henry
9
Inductance of a Toroid

10.  The magnetic flux density for toroid for any radius r such that
a<r<b is given by,
B = (µo NI)/2πr
 The flux linkage is given by
 The flux linkage = Nφ
 For a Toroid with N turns with h as the height of the toroid ,‘a’
as the inner radius and ‘b’ as the outer radius ,the inductance is
given by
10

11. Inductance of a Coaxial Cable
✘ Consider a coaxial cable with inner conductor radius ‘a’ and outer conductor
radius ‘b’
✘ Let current through the coil be I.
✘ Region 1: For radius a <ρ <b
✘ In coaxial cable, field intensity at any point between
inner and outer conductor is,
✘ We know that B= µH.
✘ Total flux is given by
11

12. ✘ Thus the inductance for region 1 is calculated as,
✘ Region 2: For radius 0 <ρ <a
✘ In coaxial cable, B at any point inside the inner conductor
is given by,
12
Inductance of a Coaxial Cable

13. ✘ Let J be the uniform current density in the solid inner conductor. For a current I, the
current density is given by
✘ The current enclosed for any radius ρ <a will be I´=Jπρ2
I´=(I/ πa2) πρ2 = I(ρ2/ a2)
✘ Thus, the total flux linkages within the differential flux element are
13
Inductance of a Coaxial Cable

14. ✘ For length l of the cable,
✘ The inductance for region 1 is given by,
 The inductance of the coaxial cable is the sum due to region1 and region 2
 or the inductance per length is
14
Inductance of a Coaxial Cable
H/m

15. 15
THANK YOU