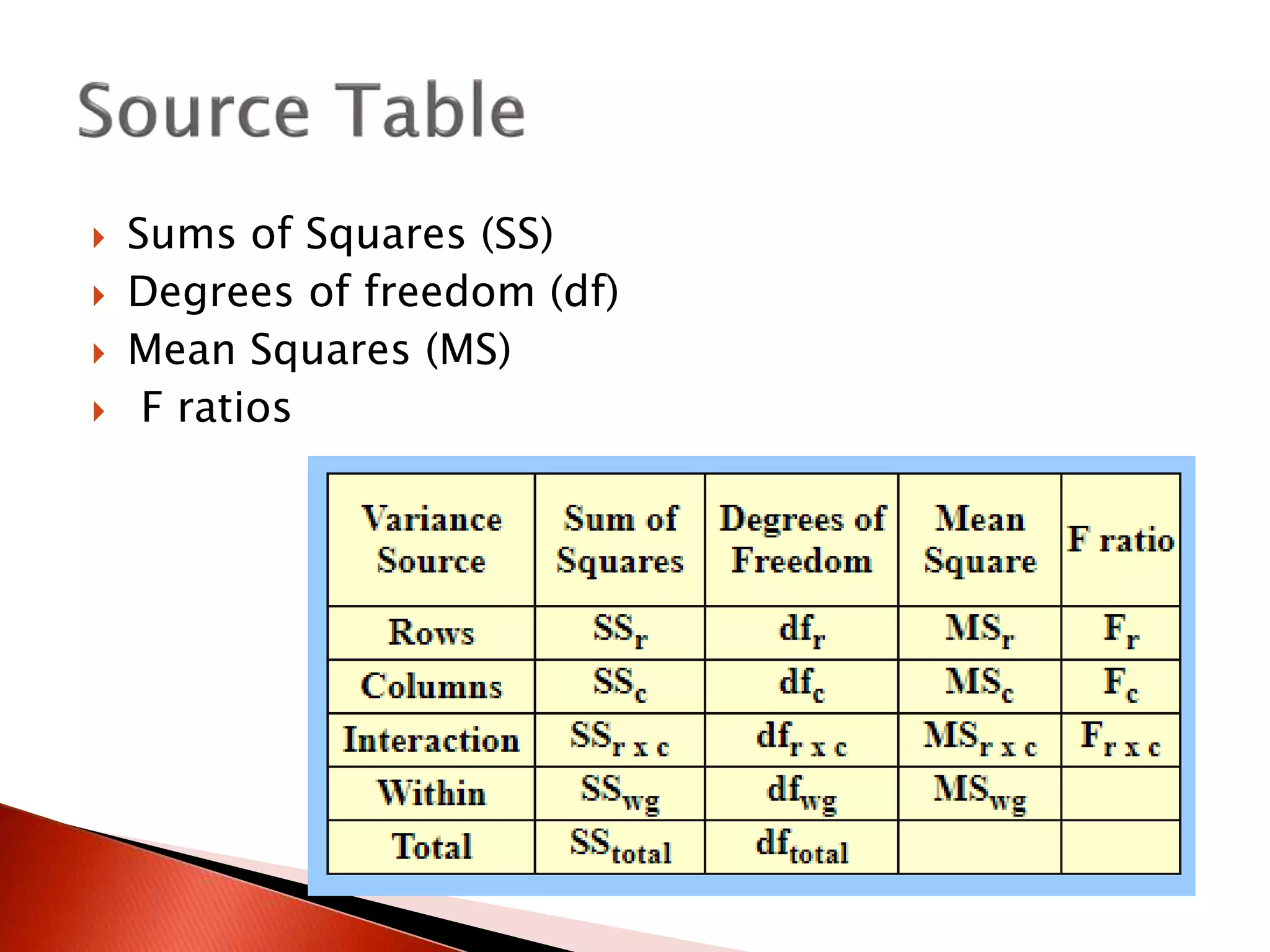
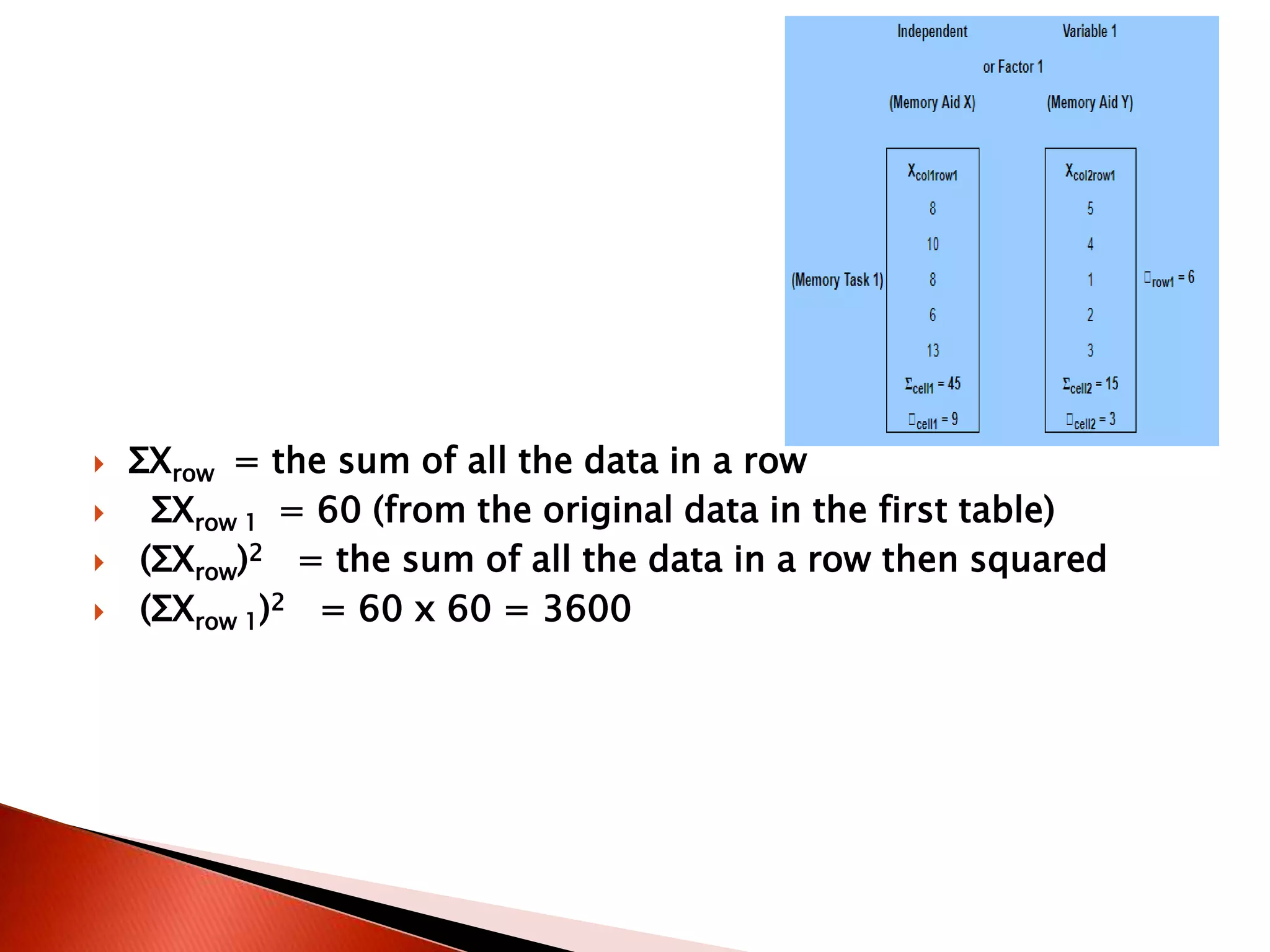
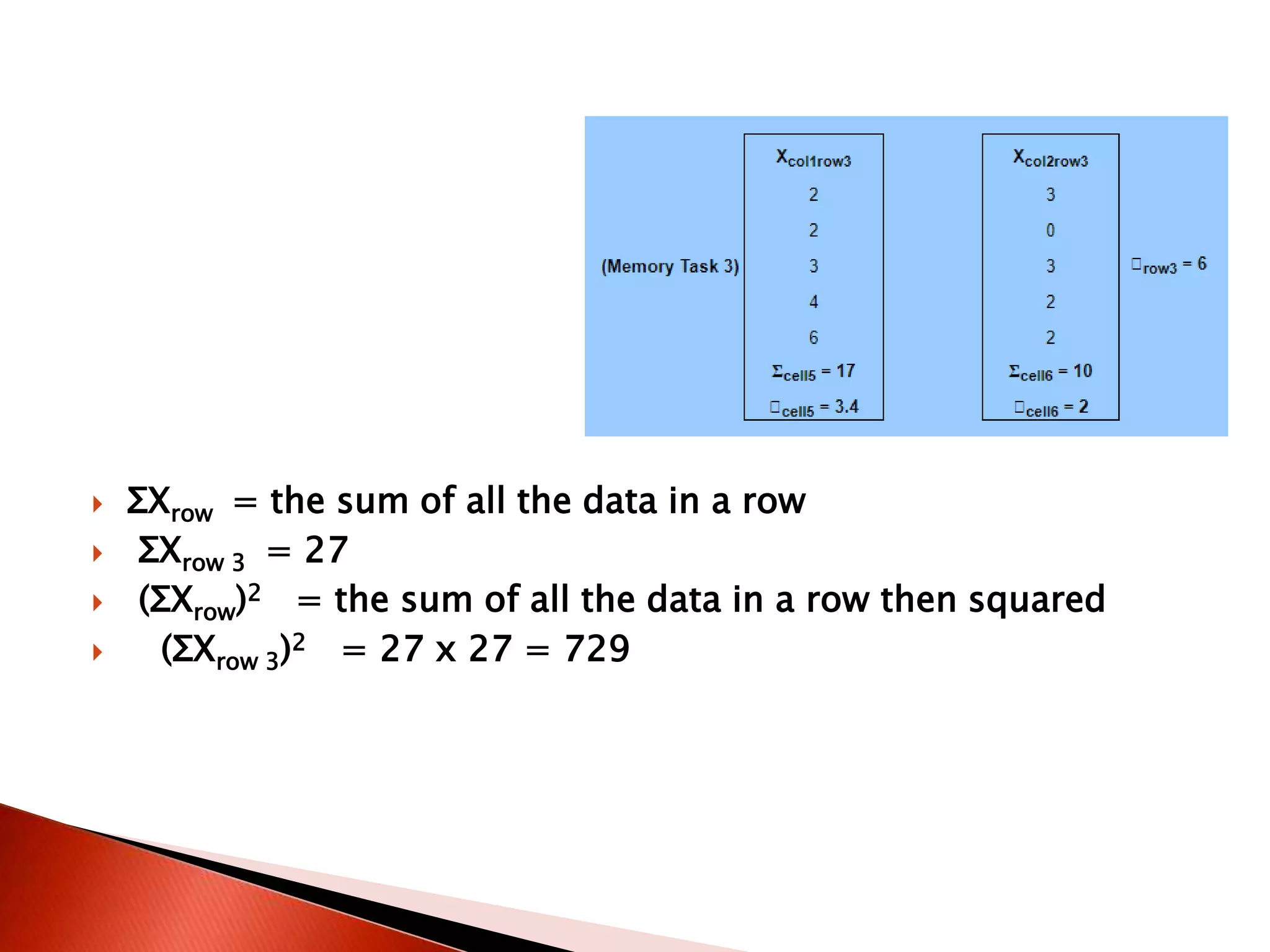
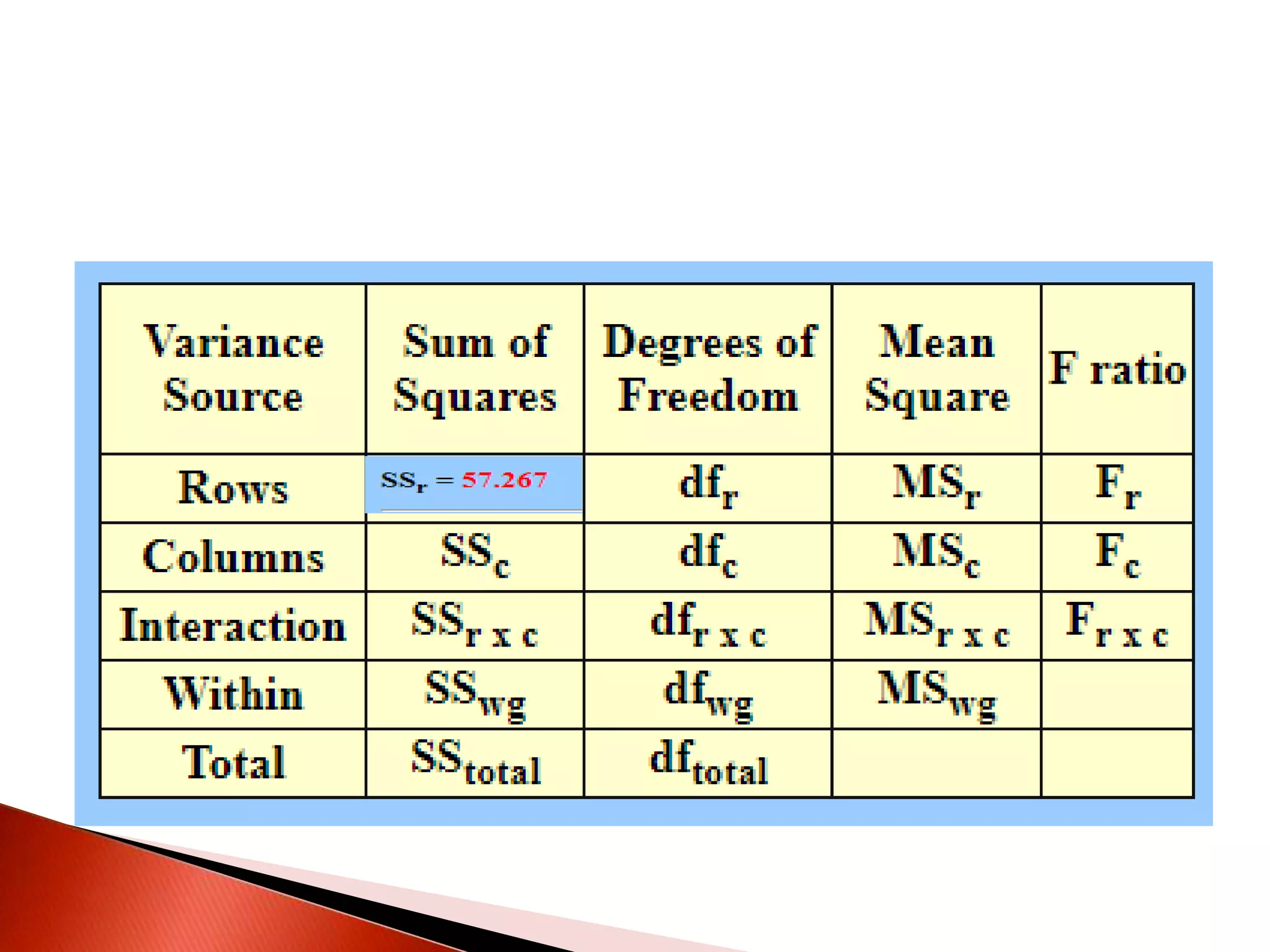
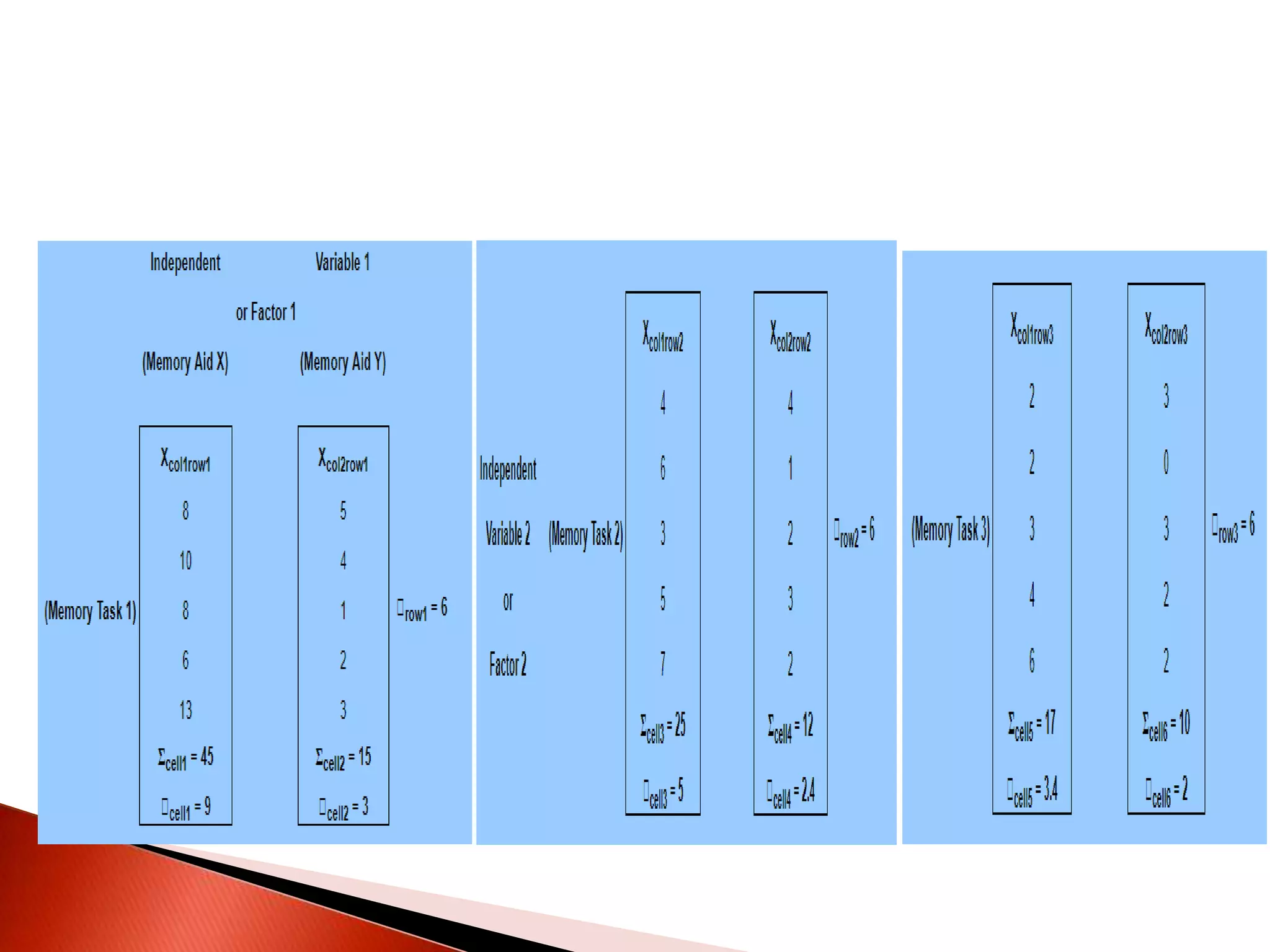
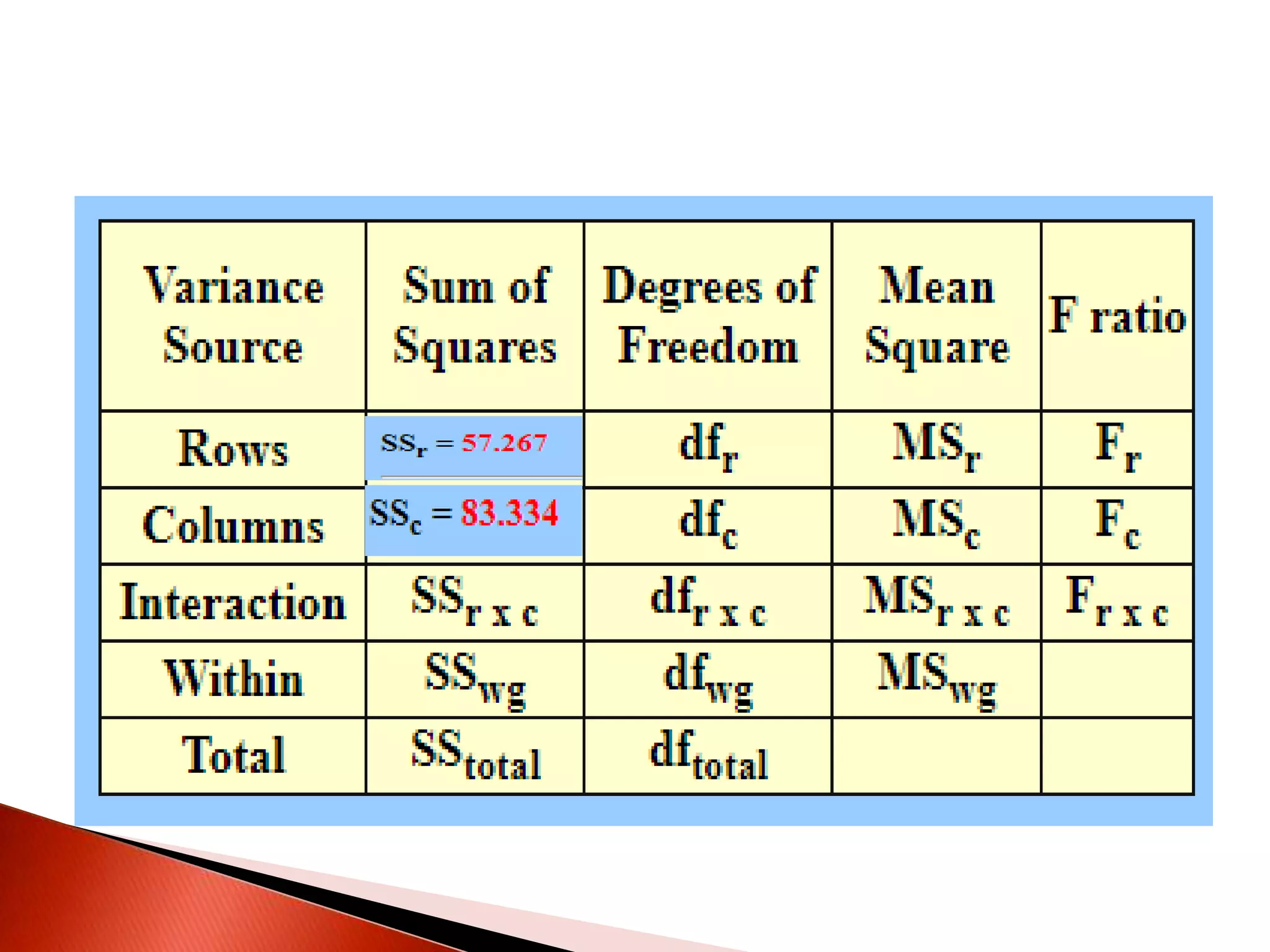
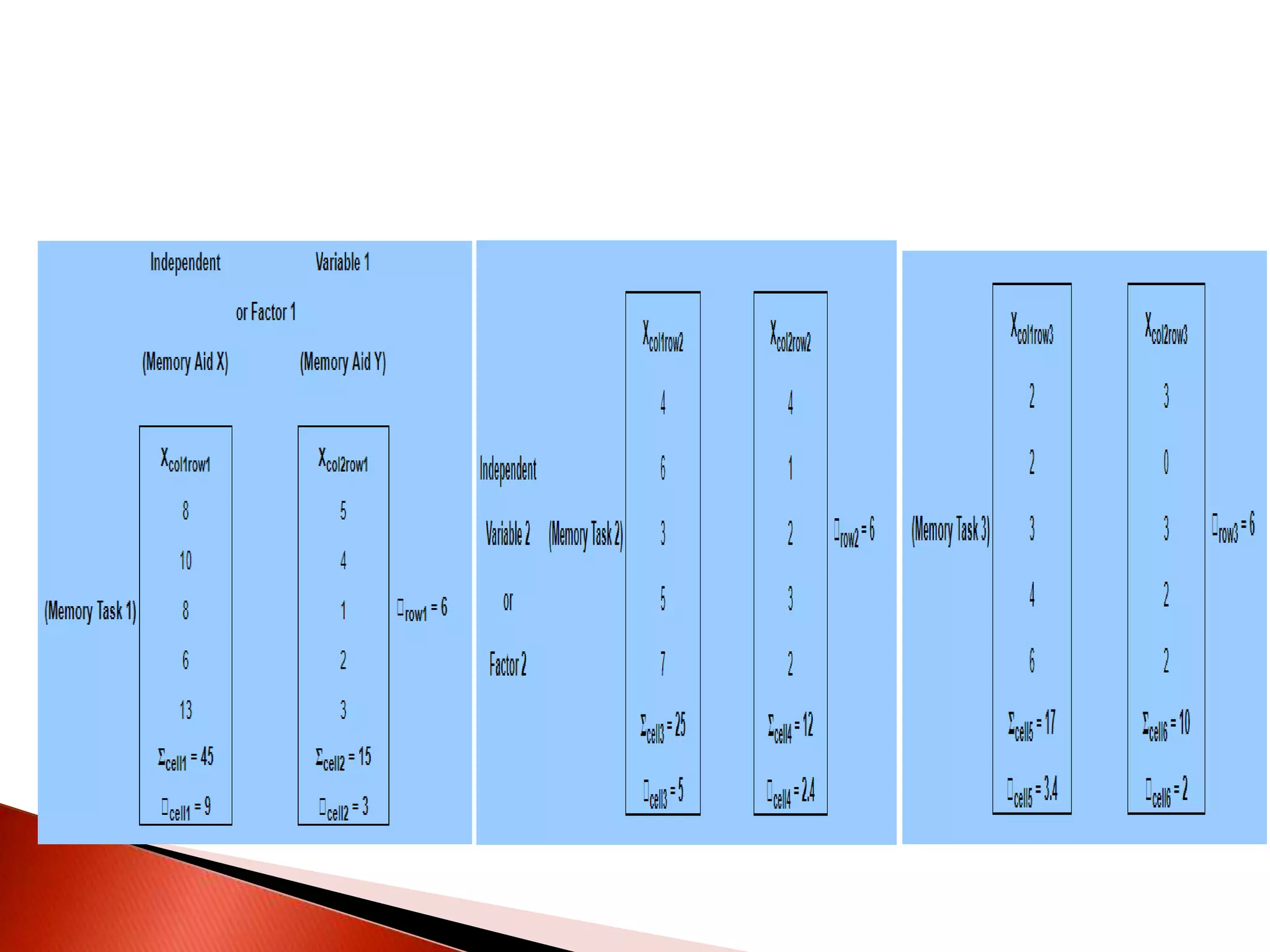
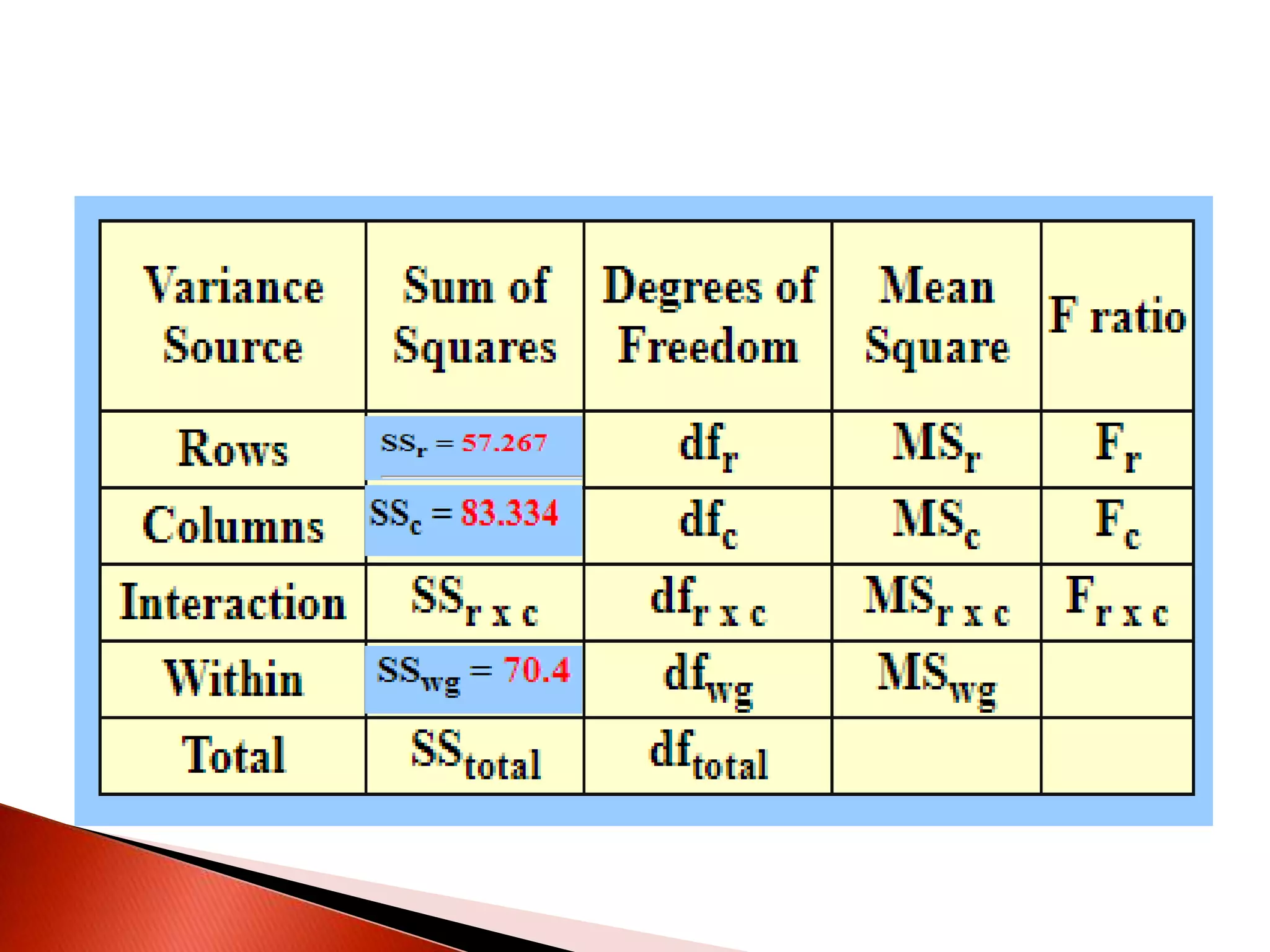
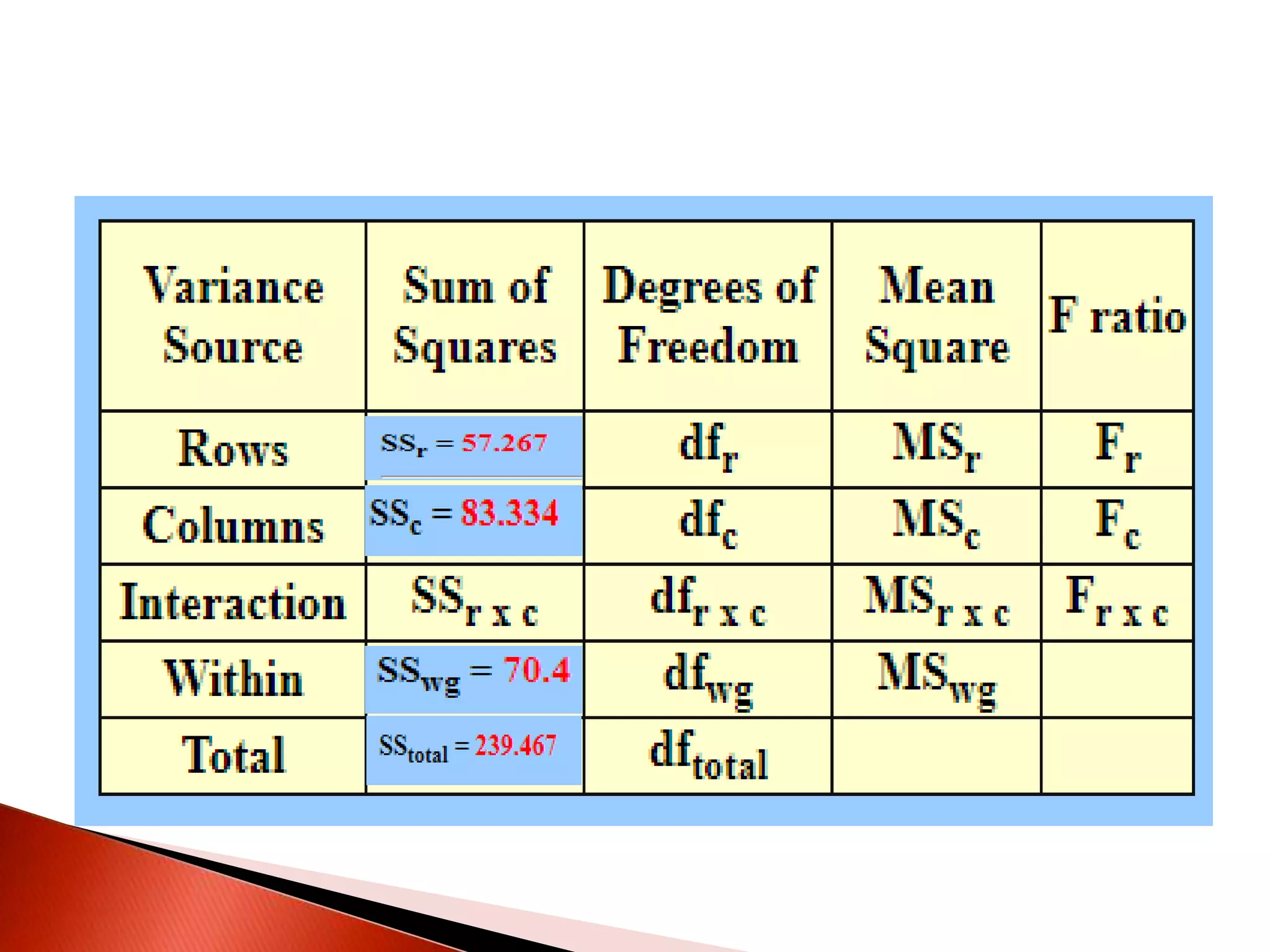
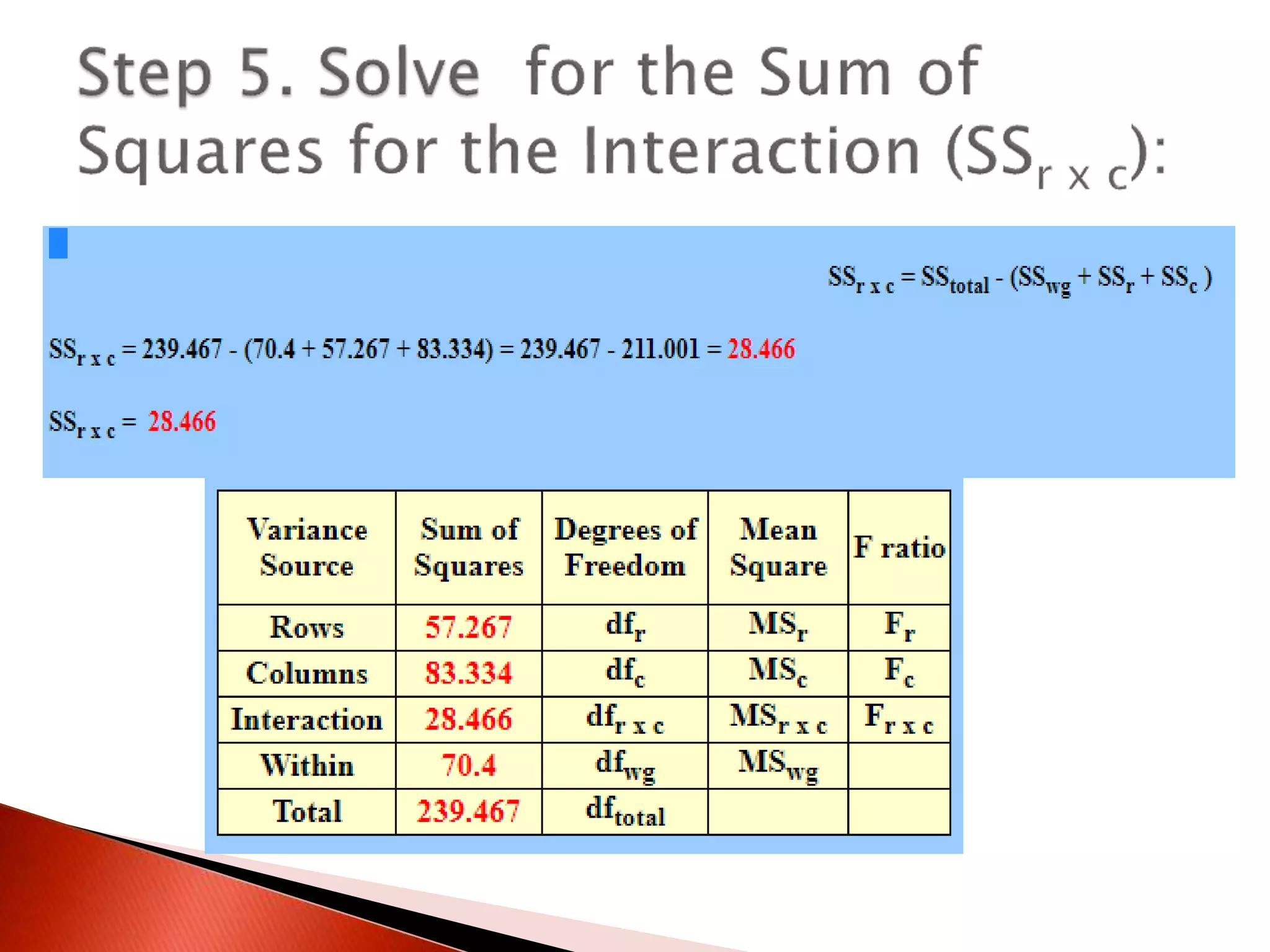
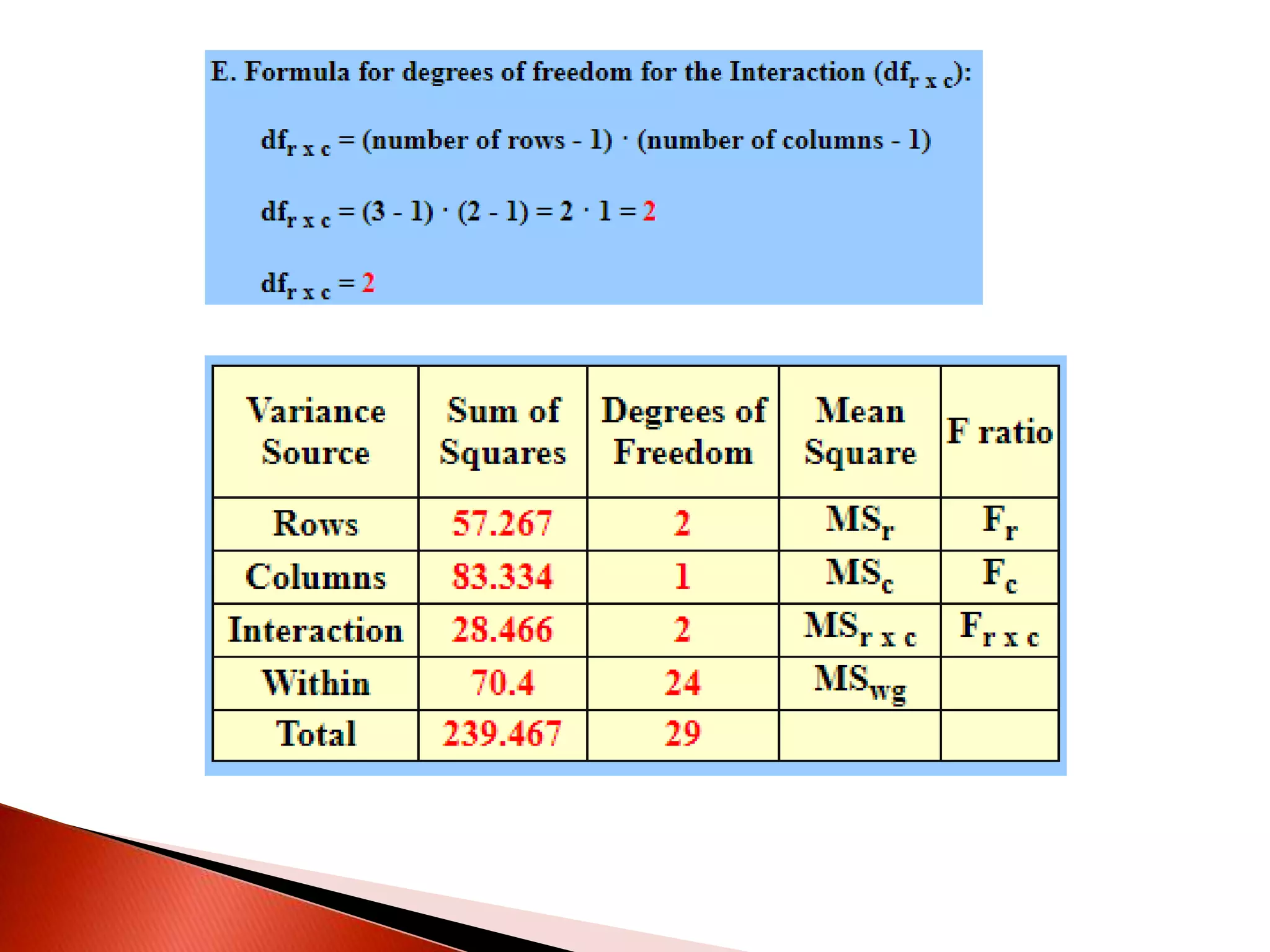
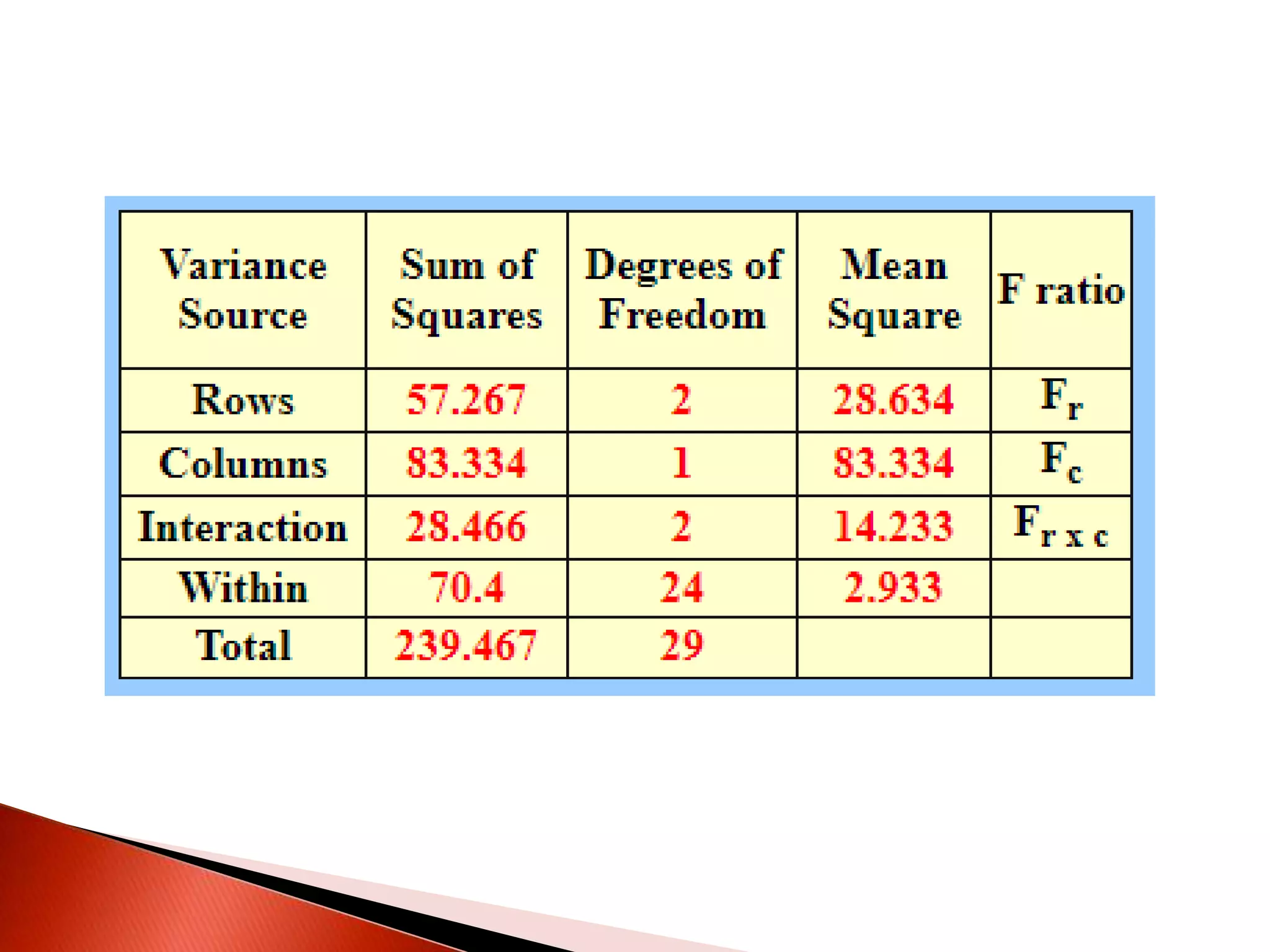
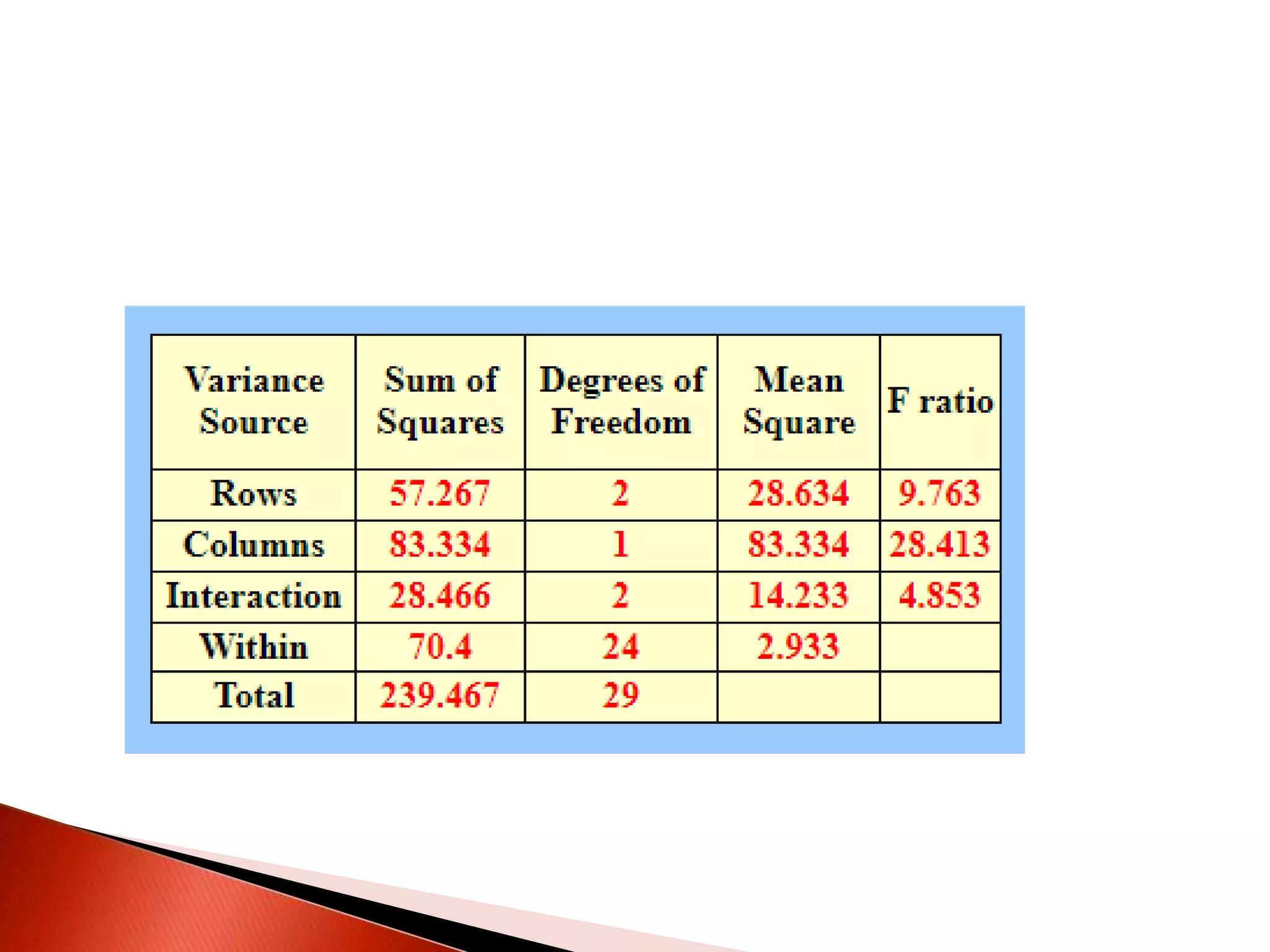
Two-way ANOVA is used to analyze data with two independent variables that have multiple levels. This document describes a memory experiment with two independent variables: type of memory aid and memory task. It provides the null and research hypotheses for the main effects of each independent variable and their interaction. Formulas are given for calculating sums of squares, degrees of freedom, mean squares, and F-ratios to determine if the main effects or interaction are statistically significant.

1. Prepared By: Randel Roy Raluto LPT
MAED-Mathematics
University of Visayas

2.  Two-Way ANOVA is used for data analysis
when you have two independent variables
(Two-Way) and 2 or more levels of either or
both independent variables.

3.  In this memory experiment, one factor or
independent variable is type of Memory Aid
that the subjects are exposed to.

4.  the effect that an independent variable has on
the dependent variable.
 there is always be two Main Effects since
there will always be two independent
variables or Factors of the experiment.

5.  The null hypothesis for the Main Effect of the
columns is:
 H0 col : µcol 1 = µcol 2 = . . . µcol k
 The null hypothesis for the Main Effect of the
rows is:
 H0 row : µrow 1 = µrow 2 = . . . µrow k

6.  The research hypothesis for the Main Effect
of the columns is:
 H1 col : At least one of the column samples
comes from a different population
distribution than the others
 The research hypothesis for the Main Effect of
the columns is:
 H1 row : At least one of the row samples
comes from a different population
distribution than the others

7.  is the effect of the combination of the two
independent variables on the dependent
variable.
 It is best seen by graphing the means of all
levels of both factors.

8.  The null hypothesis for the interaction is:
 H0 r x c : The effect of one independent
variable (IV) on the dependent variable is
unaffected by the other IV.
 The research hypothesis for the interaction is:
 H1 r x c : The effect of one independent
variable (IV) on the dependent variable is
affected by the other IV.

9.  Sums of Squares (SS)
 Degrees of freedom (df)
 Mean Squares (MS)
 F ratios

11.  Where As:
ΣXrow = the sum of all the data in a row
(ΣXrow)2 = the sum of all the data in a row then squared
Σ(ΣXrow)2 = the sum of all the values above
nrow = the number of scores in each row.
(ΣΣX)2 = the sum of the sums of all the X values for all the
cells, then squared
Ntotal = the total number of scores in all samples combined.

12.  ΣXrow = the sum of all the data in a row
 ΣXrow 1 = 60 (from the original data in the first table)
 (ΣXrow)2 = the sum of all the data in a row then squared
 (ΣXrow 1)2 = 60 x 60 = 3600

13.  ΣXrow = the sum of all the data in a row
 Xrow 2 = 37
 (ΣXrow)2 = the sum of all the data in a row then squared
 (ΣXrow 2)2 = 37 x 37 = 1369

14.  ΣXrow = the sum of all the data in a row
 ΣXrow 3 = 27
 (ΣXrow)2 = the sum of all the data in a row then squared
 (ΣXrow 3)2 = 27 x 27 = 729

15.  Σ(ΣXrow)2 = the sum of all the values above
 Σ(ΣXrow)2 = 3600 + 1369 + 729 = 5698
 nrow = the number of scores in each row
 nrow = 5 + 5 = 10

16.  (ΣΣX)2 = the sum of the sums of all the X
values for all the cells, then squared
 ΣΣX = 45 + 15 + 25 + 12 + 17 + 10 = 124
 (ΣΣX)2 = 124 x 124 = 15376
 Ntotal = the total number of scores in all
samples combined
 Ntotal = 5 + 5 + 5 + 5 + 5 + 5 = 30

19. Formula:

44.  the degrees of freedom are 2 and 24
respectively and the F is 9.763. This is often
written as F(2,24) = 9.763.
 If we look up the critical F value for Rows we
find it to be 3.40 so our Main Effect for Rows
is Significant at the 0.05 level of significance
and we can reject the null hypothesis and
conclude that at least one of the Memory
Tasks is significantly different from another.

45.  For the Main Effect for Columns the degrees
of freedom are 1 and 24 respectively and the
F is 28.413. This is often written as F(1,24) =
28.413.
 If we look up the critical F value for Columns
we find it to be 4.26 so our Main Effect for
Columns is Significant at the 0.05 level of
significance and we can reject the null
hypothesis and conclude that Memory Aids X
and Y are significantly different from each
other.

46.  For the Interaction the degrees of freedom
are 2 and 24 respectively and the F is 4.853.
This is often written as F(2,24) = 4.853.
 If we look up the critical F value for Columns
we find it to be 3.40 so our Main Effect for
the Interaction is Significant at the 0.05 level
of significance and we can reject the null
hypothesis and conclude that there is a
significant Interaction between Memory Aids
and Memory Tasks.