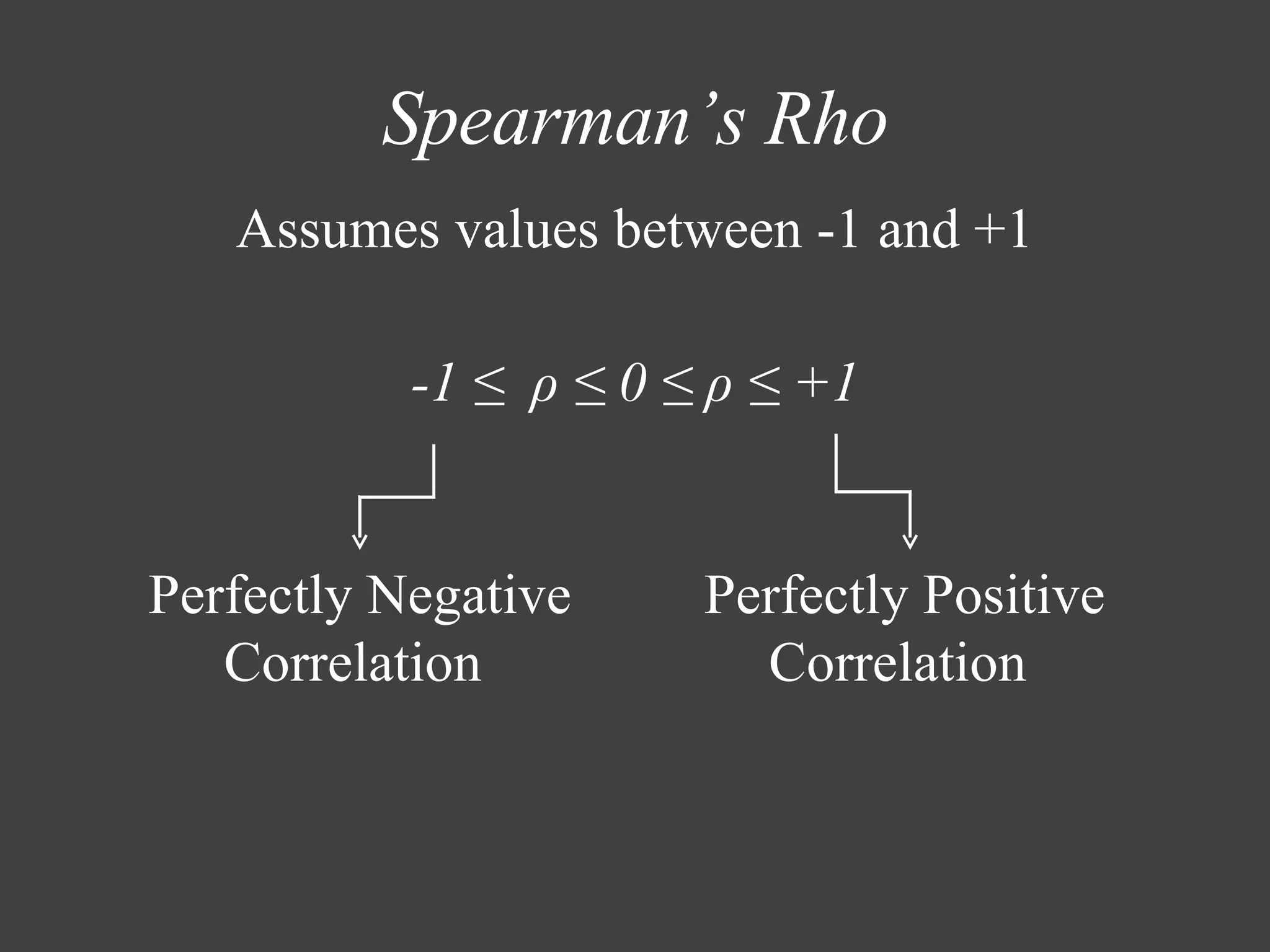
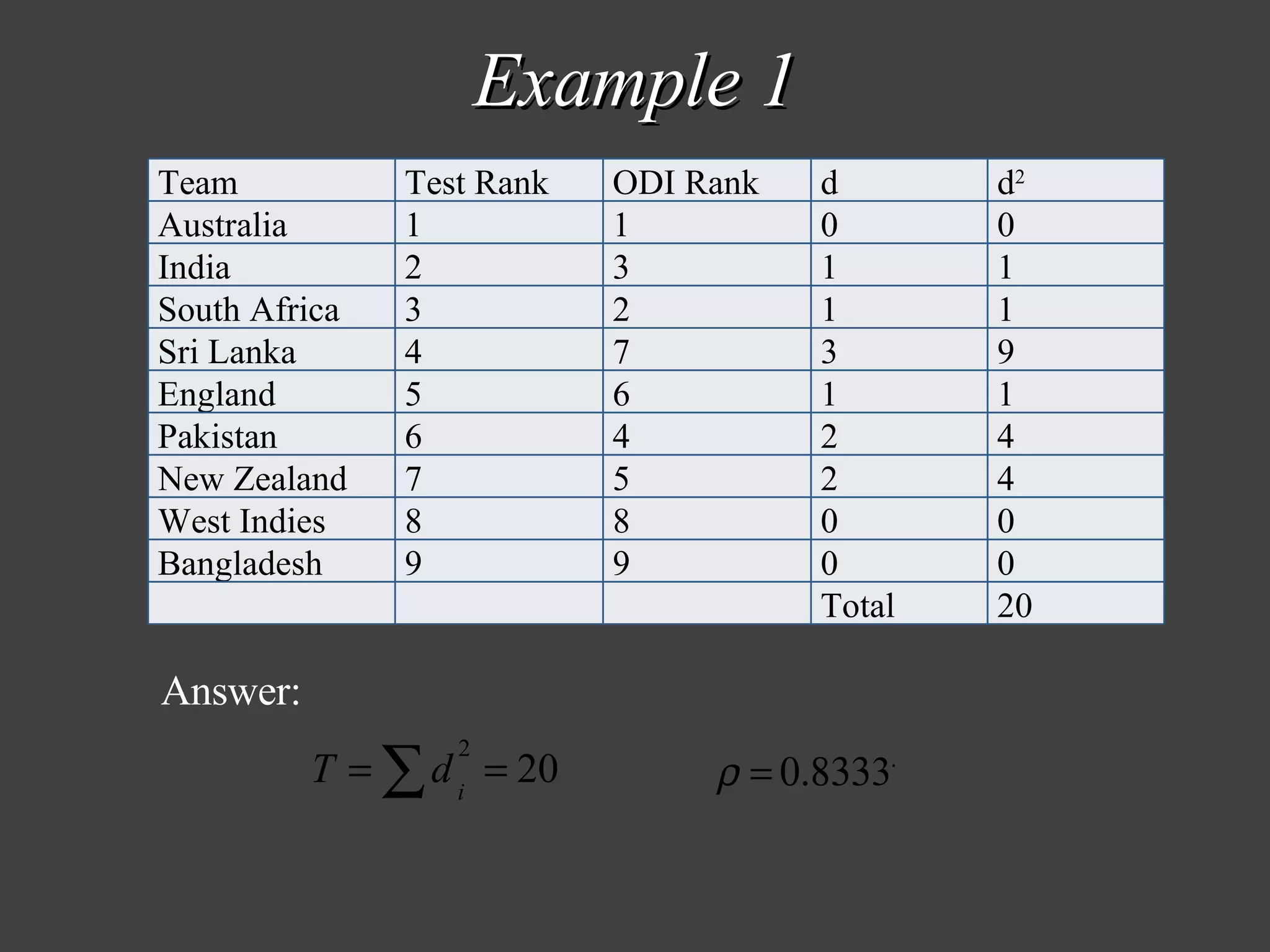
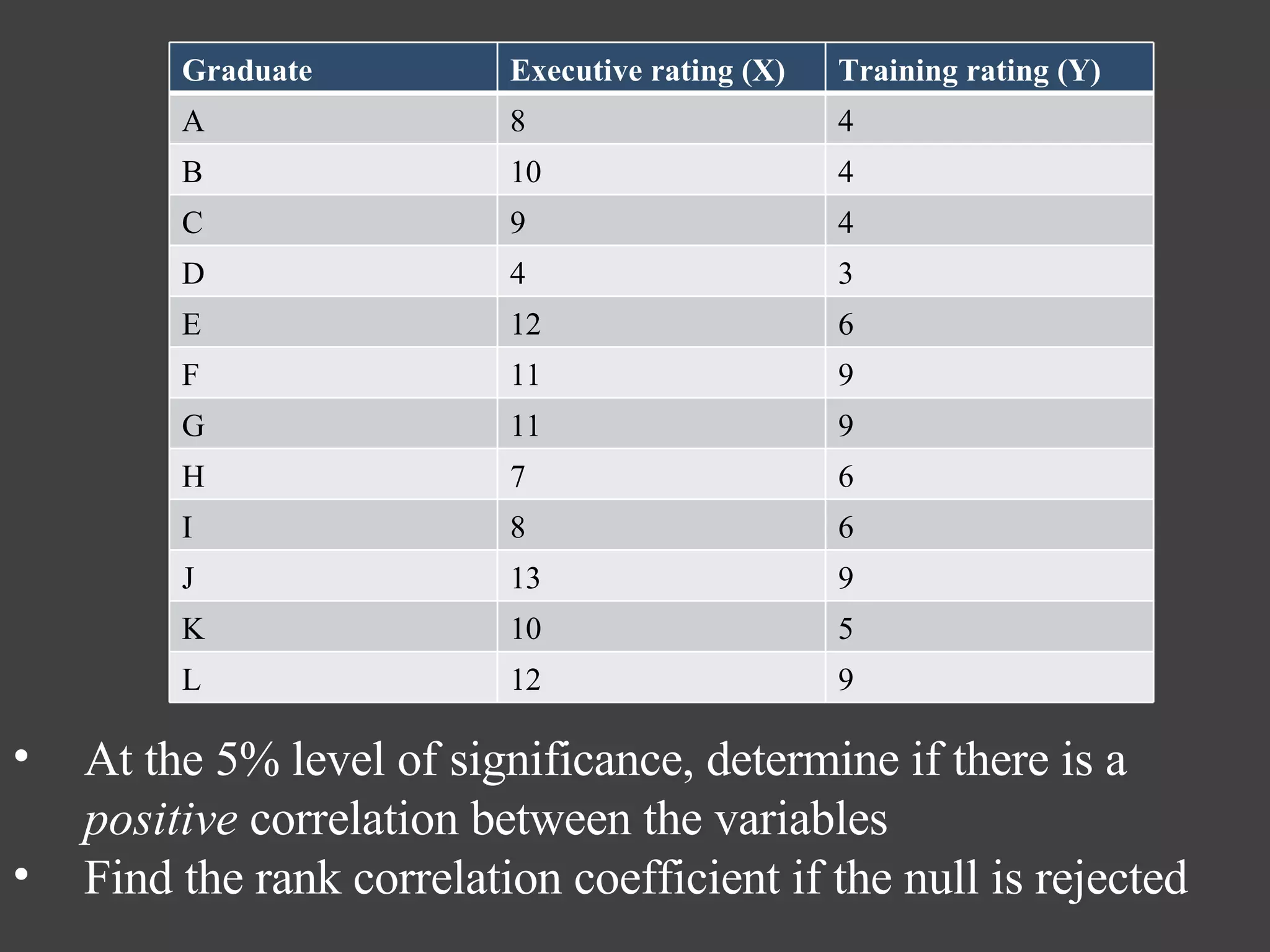
The document discusses Spearman's rank correlation coefficient, a nonparametric measure of statistical dependence between two variables. It assumes values between -1 and 1, with -1 indicating a perfect negative correlation and 1 a perfect positive correlation. The steps involve converting values to ranks, calculating the differences between ranks, and determining if there is a statistically significant correlation based on the test statistic and critical values. An example calculates Spearman's rho using rankings of cricket teams in test and one day international matches.

1. Spearman Rank Correlation A measure of Rank Correlation Group 3

2. The Spearman Correlation Spearman’s correlation is designed to measure the relationship between variables measured on an ordinal scale of measurement. Similar to Pearson’s Correlation, however it uses ranks as opposed to actual values.

3. Assumptions The data is a bivariate random variable. The measurement scale is at least ordinal. X i , Y i is independent of X j , Y j where i ≠ j

4. Advantages Less sensitive to bias due to the effect of outliers - Can be used to reduce the weight of outliers (large distances get treated as a one-rank difference) Does not require assumption of normality. When the intervals between data points are problematic, it is advisable to study the rankings rather than the actual values.

5. Disadvantages Calculations may become tedious. Additionally ties are important and must be factored into computation.

6. Steps in Calculating Spearman’s Rho Convert the observed values to ranks (accounting for ties) Find the difference between the ranks, square them and sum the squared differences. Set up hypothesis, carry out test and conclude based on findings.

7. Steps in Calculating Spearman’s Rho If the null is rejected then calculate the Spearman correlation coefficient to measure the strength of the relationship between the variables.

8. Hypothesis: I (Two-Tailed) H o : There is no correlation between the Xs and the Ys. (there is mutual independence between the Xs and the Ys) H 1 : There is a correlation between the Xs and the Ys. (there is mutual dependence between the Xs and the Ys)

9. Hypothesis: II B. (One-Tailed - Lower) H o : There is no correlation between the Xs and the Ys. (there is mutual independence between the Xs and the Ys) H 1 : There is a negative correlation between the Xs and the Ys.

10. Hypothesis: III C. (One-Tailed - Upper) H o : There is no correlation between the Xs and the Ys. (there is mutual independence between the Xs and the Ys) H 1 : There is a positive correlation between the Xs and the Ys.

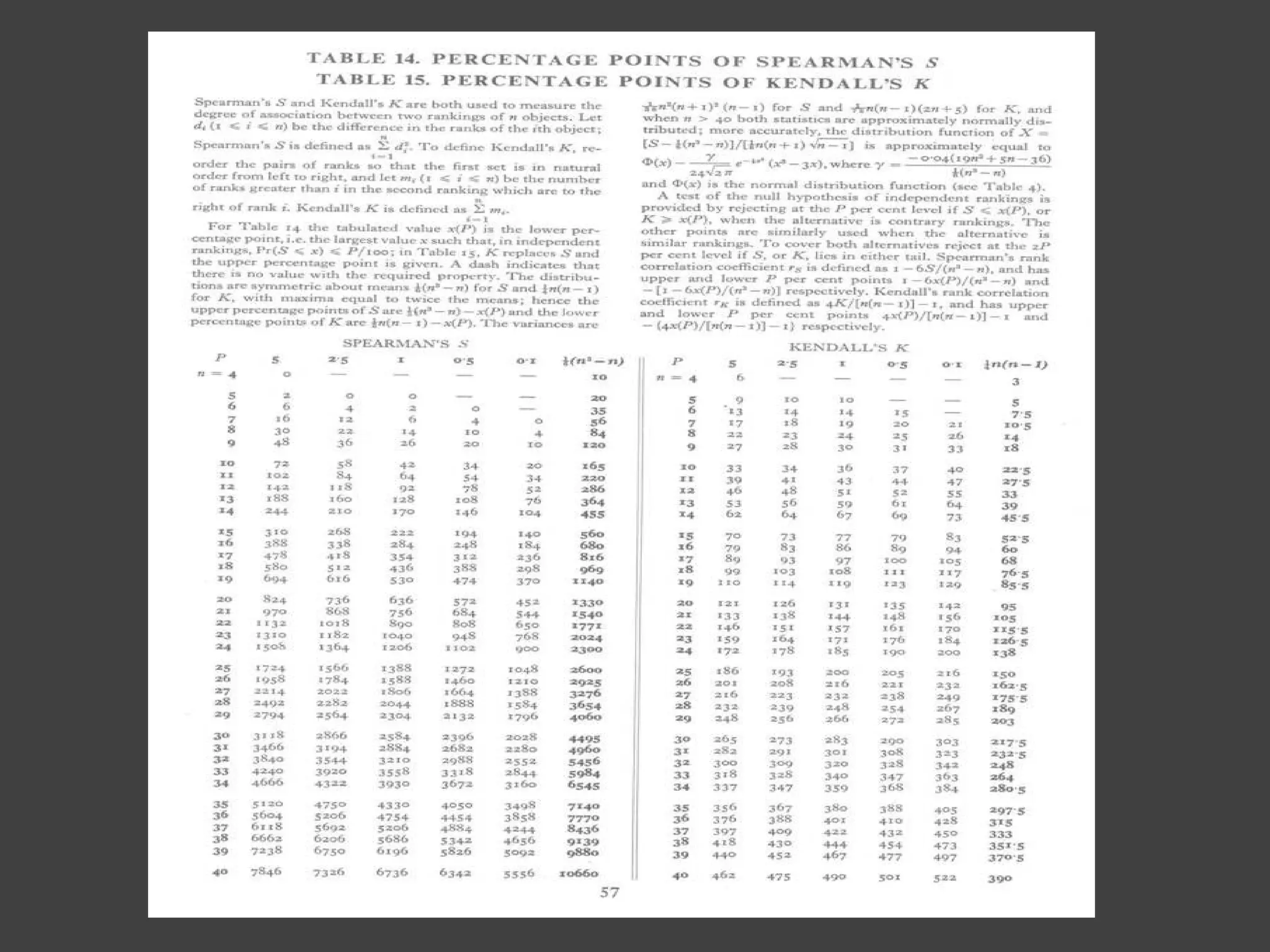
11. Test Statistic For small samples (N < 40): T= Σ d i 2 = Σ [R(X i ) - R(Y i )] 2 For large samples: (Reject using the appropriate Z critical value)

12. Test Statistic In the case of a large sample:

13. Decision Rules Two-tailed: Reject H 0 if T≤ S α/2 or T > S 1- α/2 . Do not reject otherwise. B. One-tailed - Lower: Reject H 0 if T > S 1- α . Do not reject otherwise. C. One-tailed- Upper: Reject H 0 if T≤ S α . Do not reject otherwise.

14. In the case of few ties (less than 5% of the sample): Where d i is the difference in the ranks of each pair and N is the number of pairs Spearman’s Rho

15. Spearman’s Rho If there are numerous ties:

16. Spearman’s Rho Assumes values between -1 and +1 -1 ≤ ρ ≤ 0 ≤ ρ ≤ +1 Perfectly Negative Correlation Perfectly Positive Correlation

17. Example 1 The ICC rankings for One Day International (ODI) and Test matches for nine teams are shown below. Test whether there is correlation between the ranks Team Test Rank ODI Rank Australia 1 1 India 2 3 South Africa 3 2 Sri Lanka 4 7 England 5 6 Pakistan 6 4 New Zealand 7 5 West Indies 8 8 Bangladesh 9 9

18. Example 1 Answer: Team Test Rank ODI Rank d d 2 Australia 1 1 0 0 India 2 3 1 1 South Africa 3 2 1 1 Sri Lanka 4 7 3 9 England 5 6 1 1 Pakistan 6 4 2 4 New Zealand 7 5 2 4 West Indies 8 8 0 0 Bangladesh 9 9 0 0 Total 20

19. Example 2 A composite rating is given by executives to each college graduate joining a plastic manufacturing firm. The executive ratings represent the future potential of the college graduate. The graduates then enter an in-plant training programme and are given another composite rating. The executive ratings and the in-plant ratings are as follows:

20. At the 5% level of significance, determine if there is a positive correlation between the variables Find the rank correlation coefficient if the null is rejected Graduate Executive rating (X) Training rating (Y) A 8 4 B 10 4 C 9 4 D 4 3 E 12 6 F 11 9 G 11 9 H 7 6 I 8 6 J 13 9 K 10 5 L 12 9