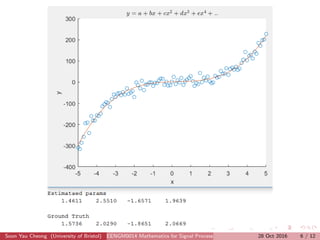
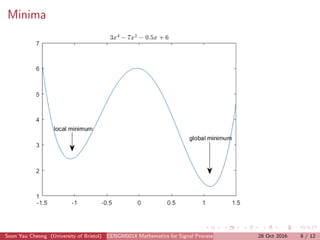
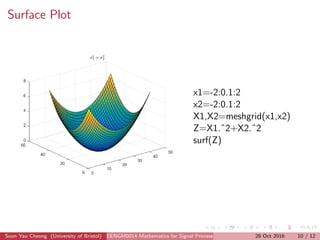
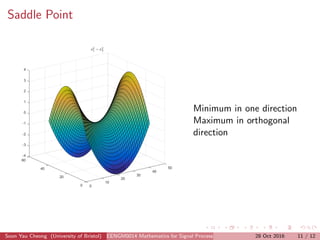
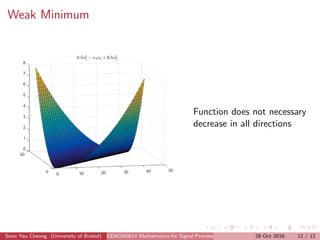
This document discusses two methods for data fitting: 1) using the pseudo-inverse of over-determined equations and 2) gradient descent. It explains that the pseudo-inverse method solves the system of equations MX=Y to estimate parameters like a, b, c, d. Gradient descent is described as iteratively updating the parameter estimates in the direction of the negative gradient to reduce the cost function. The document also covers concepts like the gradient, Hessian matrix, minima, saddle points, and weak minima.

1. EENGM0014 Mathematics for Signal Processing and
Communications
Tutorial 4
Soon Yau Cheong
University of Bristol
28 Oct 2016
Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 1 / 12

2. Data Fitting
Estimate a, b, c, d, e, ...
Can be solved with 2 methods:
1 Pseudo inverse of
over-determined equations
2 Gradient descent
Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 2 / 12

3. Overdetermined Equations
Assume y = a + bx + cx2
+ dx3
Say (x0, y0) corresponds to coordinates of first point and (xm, ym) for m-th
point. We form matrices by substituting (x,y) into polynomial equation:





1 x0 x2
0 x3
0
1 x1 x2
1 x3
1
...
...
...
...
1 xM−1 x2
M−1 x3
M−1









a
b
c
d



 =





y0
y1
...
yM−1





MX = Y
Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 3 / 12

4. Solving over-determined equations
people.csail.mit.edu/bkph/articles/Pseudo Inverse.pdf
Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 4 / 12

5. Apply pseudo inverse to our problem:
X = (MT
M)−1
MT
Y
or use Matlab function pinv
X = pinv(M) ∗ Y =




a
b
c
d




Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 5 / 12

6. Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 6 / 12

7. Gradient
First Order Partial Derivative
If y is function of X = {x1, x2, ..., xn} then
X (y) =
∂y
∂X
=








∂y
∂x1
∂y
∂x2
...
∂y
∂xn








where ∂y
∂x1
is partial derivative of y with respect to x1, with other variables
in X being held constant.
∂y
∂xi
= lim
h→∞
f (x1, ..., xi + h, ..., xn) − f (x1, ..., xi , ..., xn)
h
Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 7 / 12

8. Hessian Matrix
Second Order Partial Derivative
H =













∂2y
∂x2
1
∂2y
∂x1∂x2
· · · ∂2y
∂x1∂xn
∂2y
∂x2∂x1
∂2y
∂x2
2
· · · ∂2y
∂x2∂xn
...
...
...
...
∂2y
∂xn∂x1
∂2y
∂xn∂x2
· · · ∂2y
∂x2
n













Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 8 / 12

9. Minima
Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 9 / 12

10. Surface Plot
x1=-2:0.1:2
x2=-2:0.1:2
X1,X2=meshgrid(x1,x2)
Z=X1.ˆ2+X2.ˆ2
surf(Z)
Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 10 / 12

11. Saddle Point
Minimum in one direction
Maximum in orthogonal
direction
Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 11 / 12

12. Weak Minimum
Function does not necessary
decrease in all directions
Soon Yau Cheong (University of Bristol) EENGM0014 Mathematics for Signal Processing and Communications28 Oct 2016 12 / 12