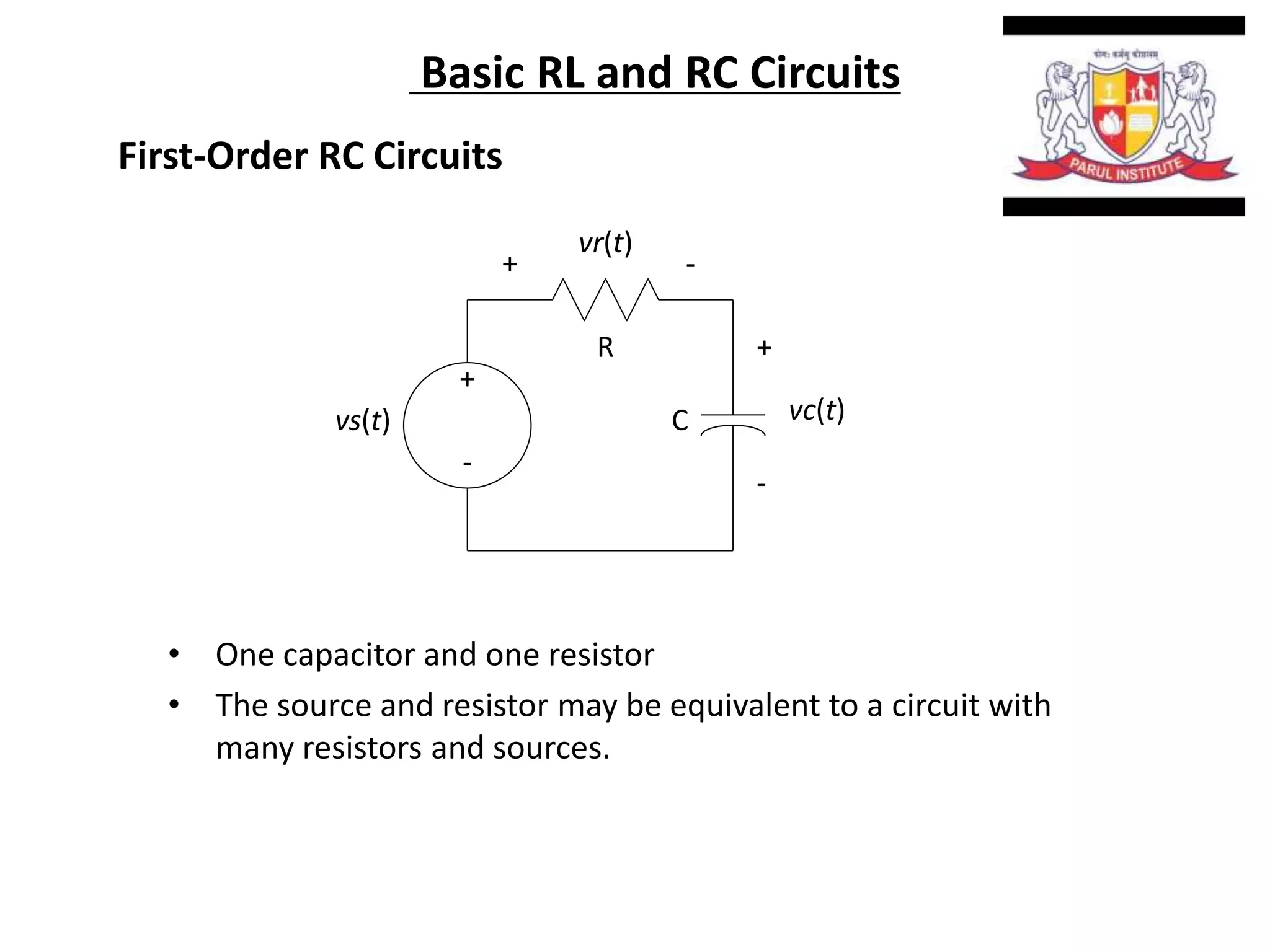
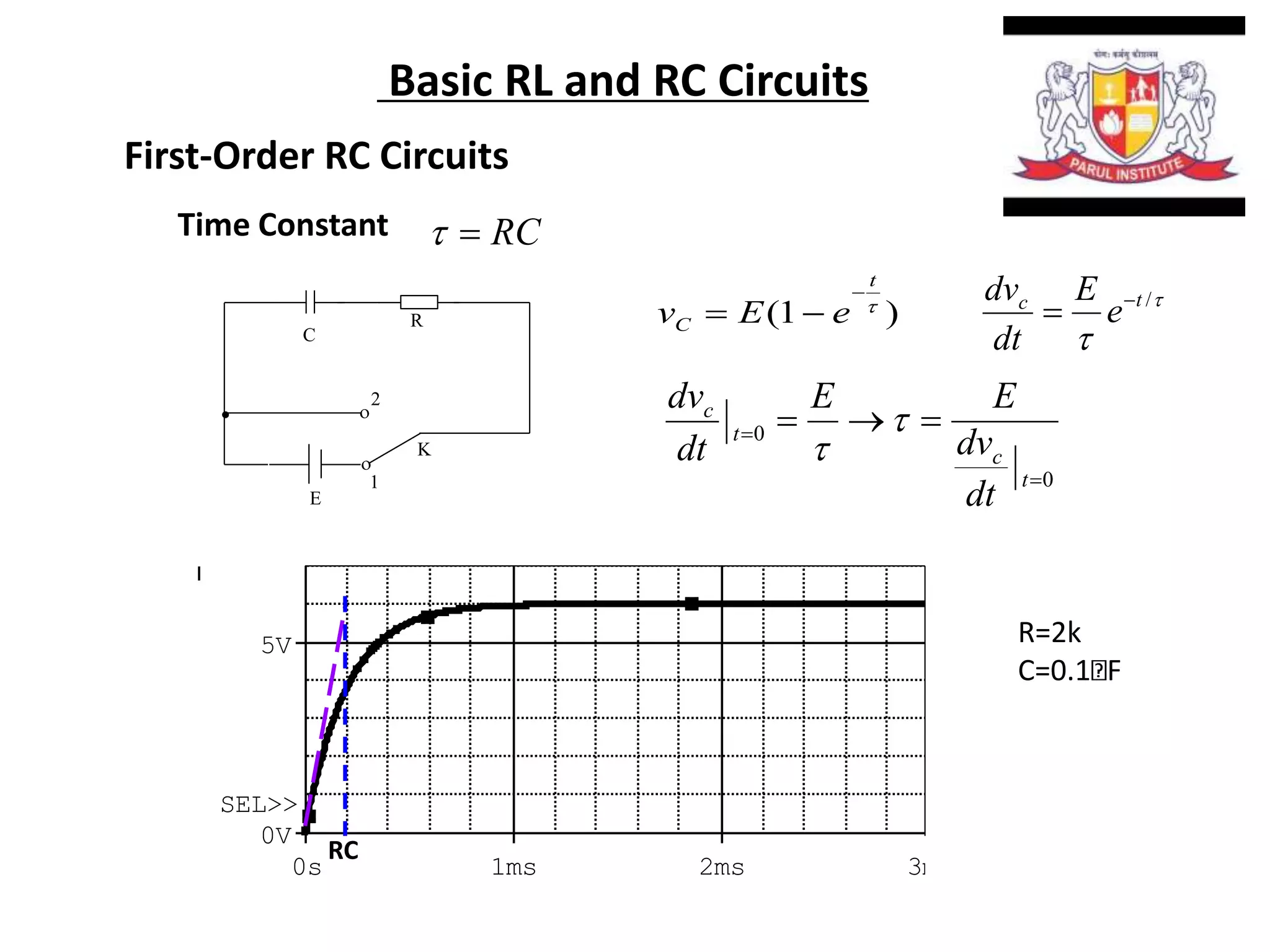
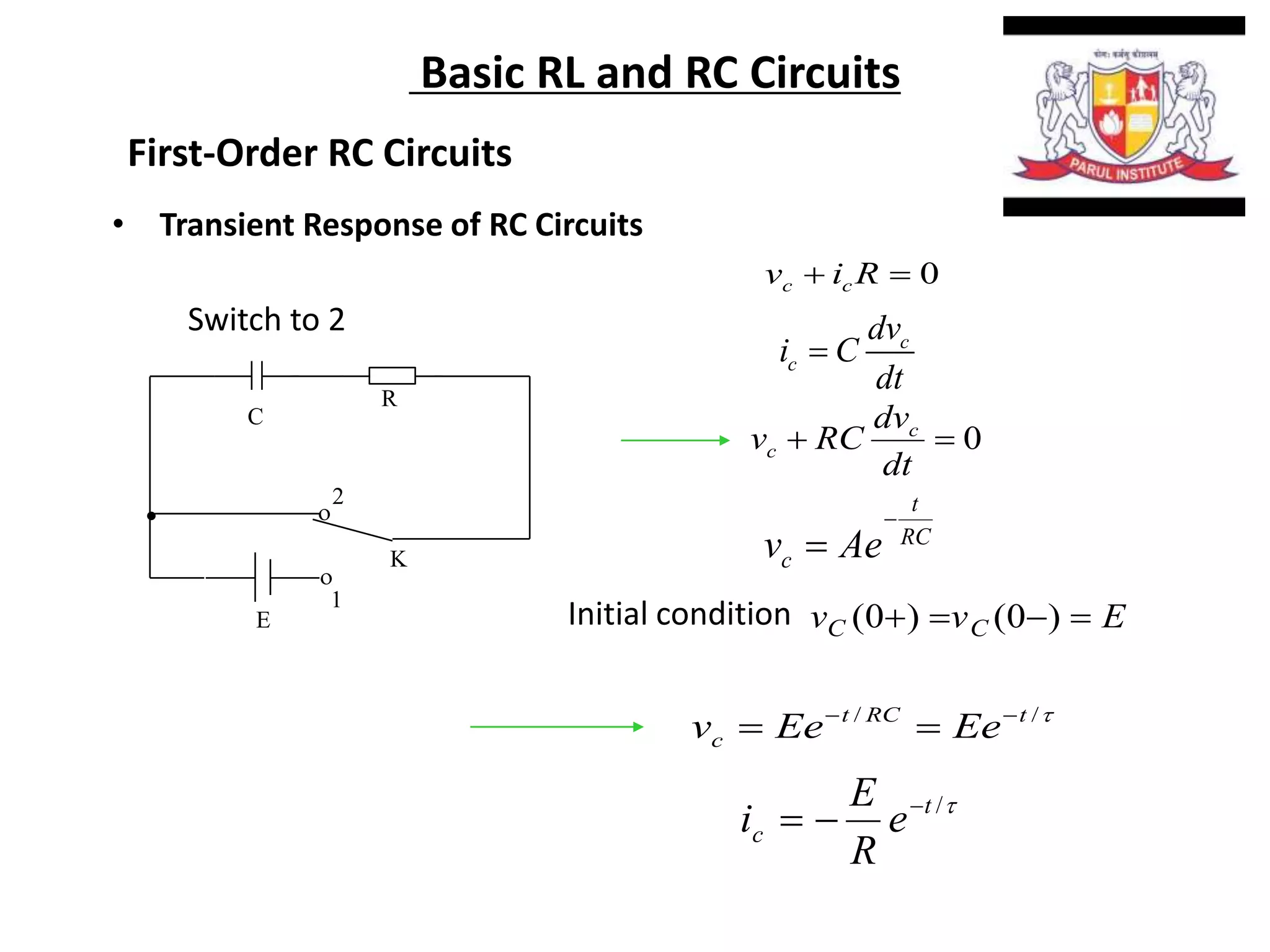
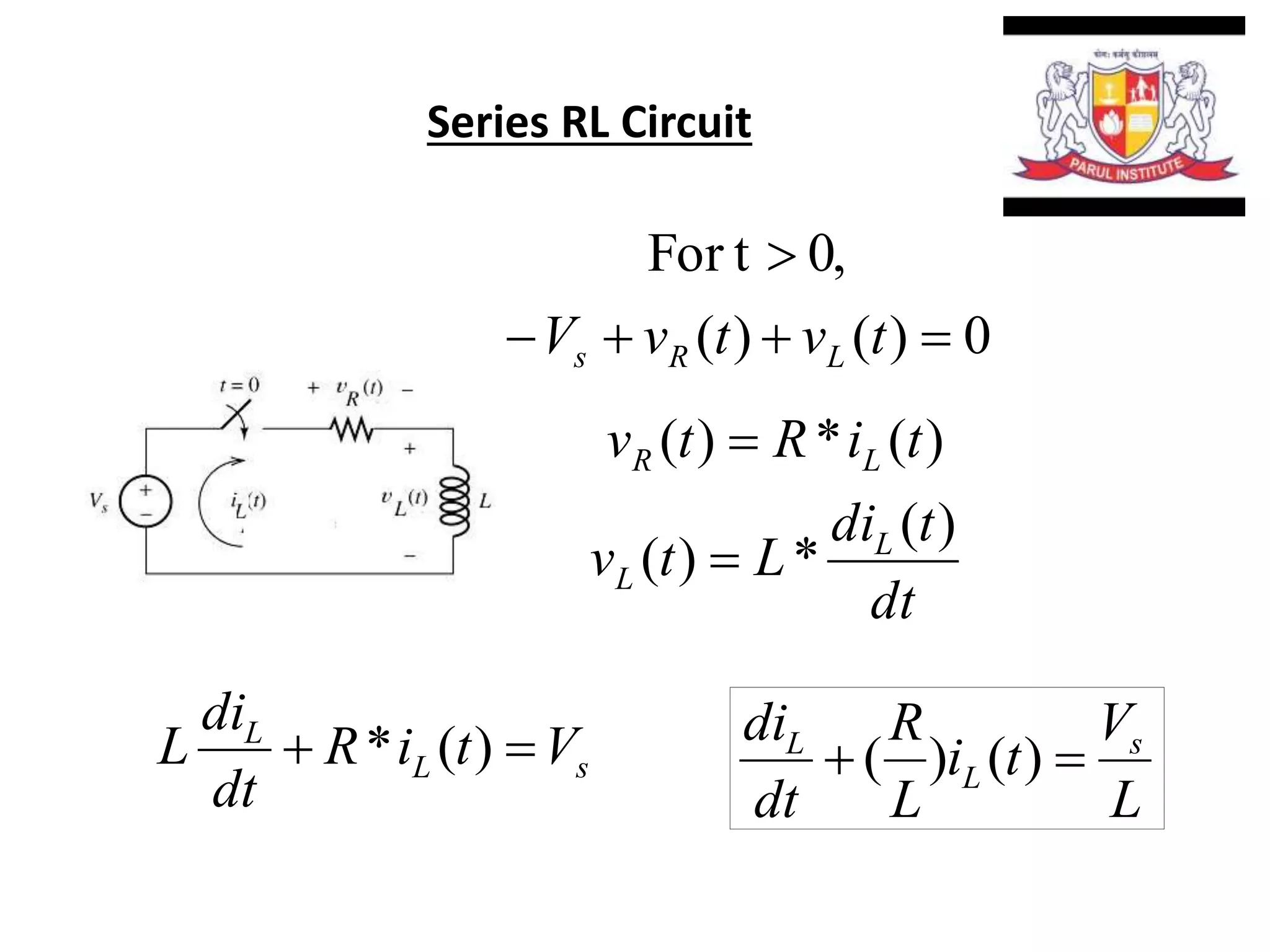
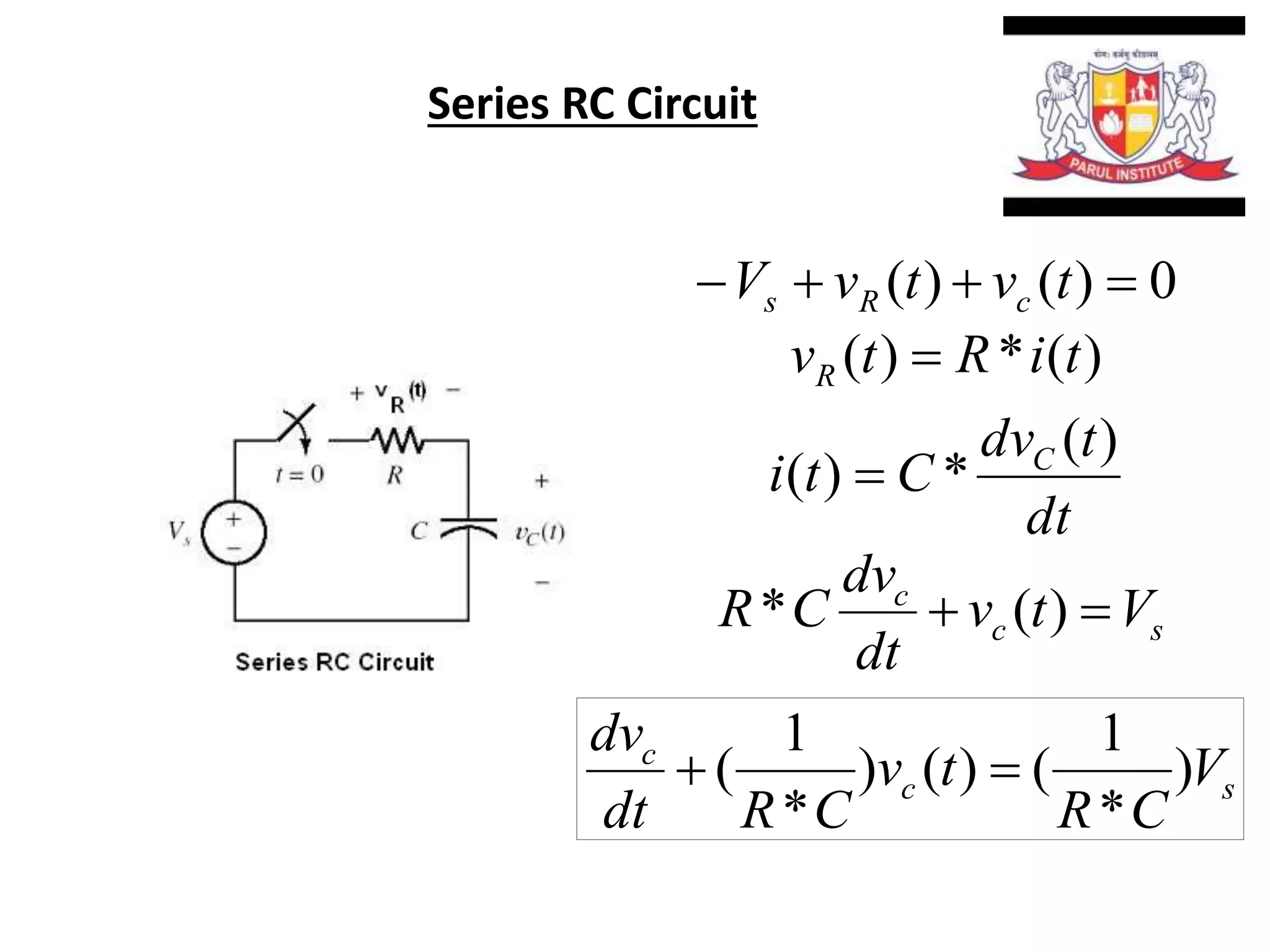
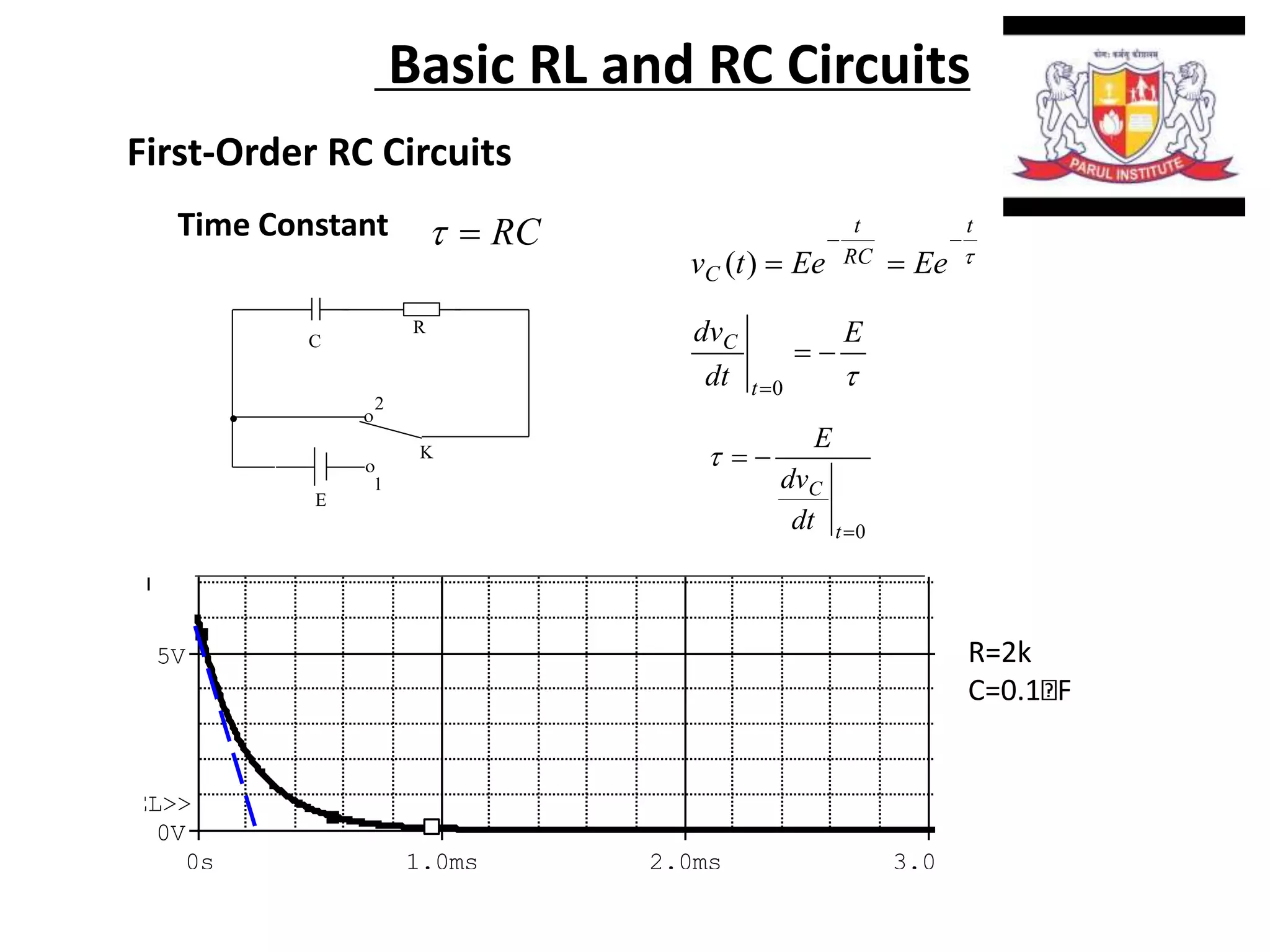
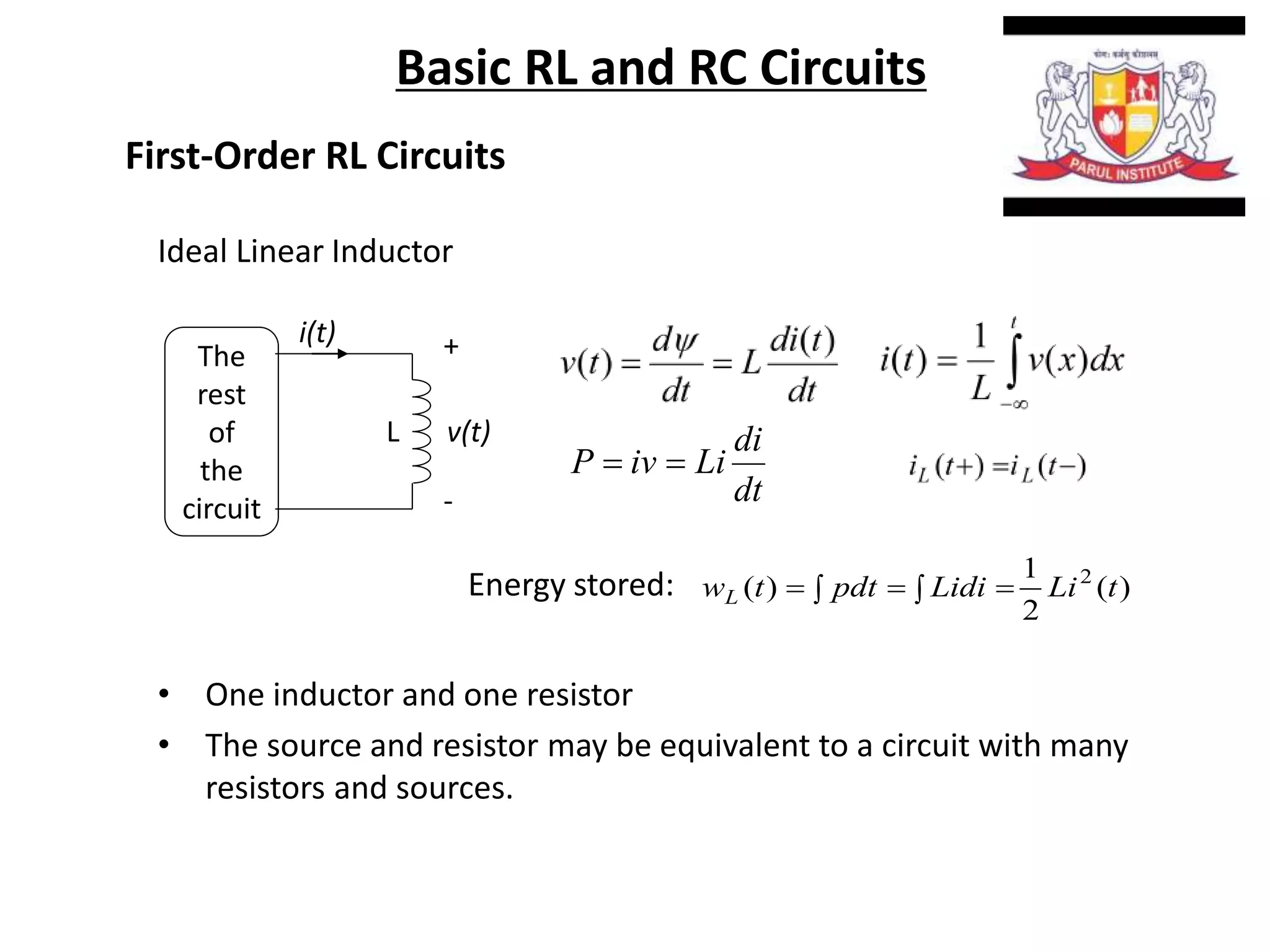
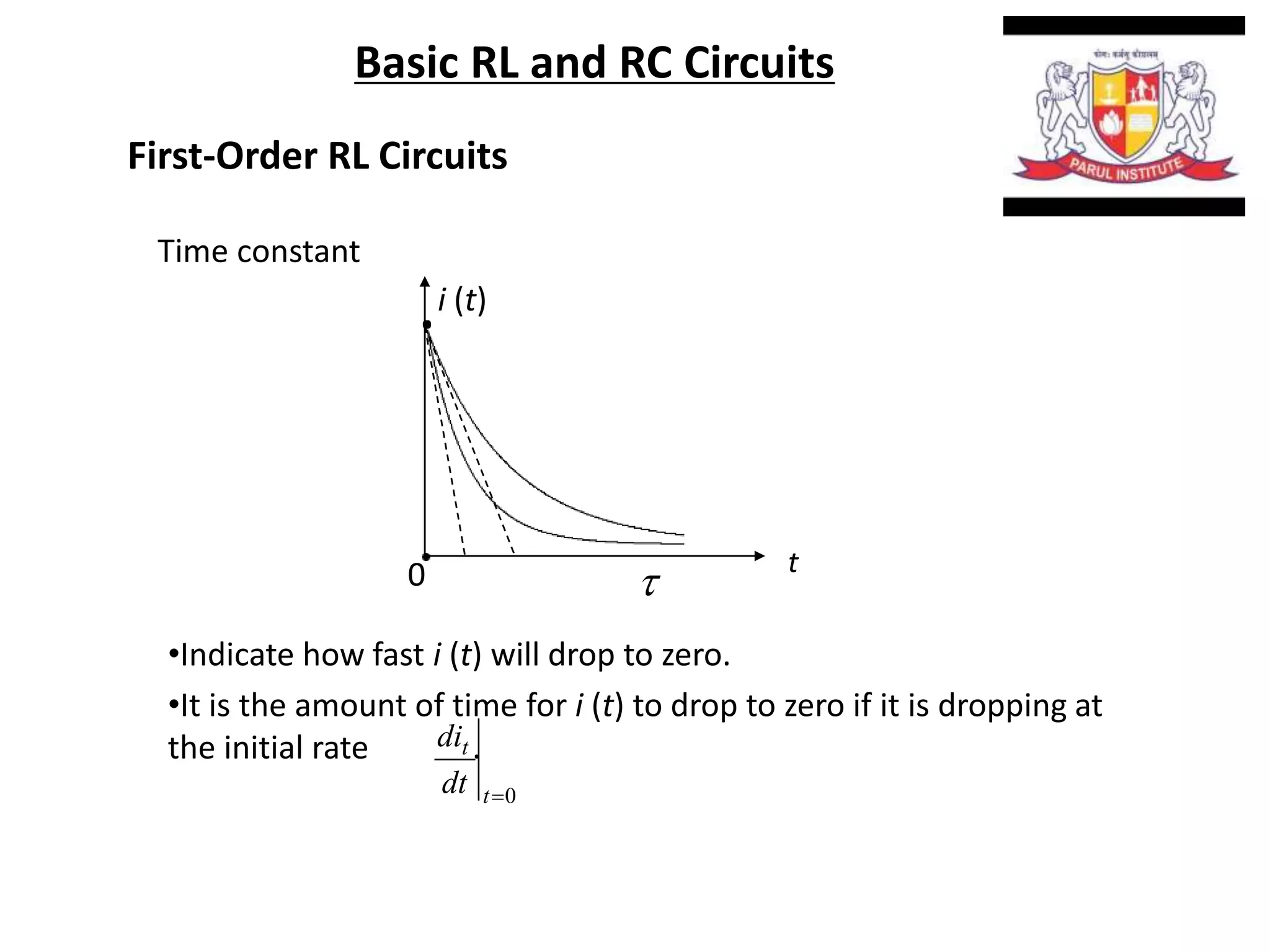
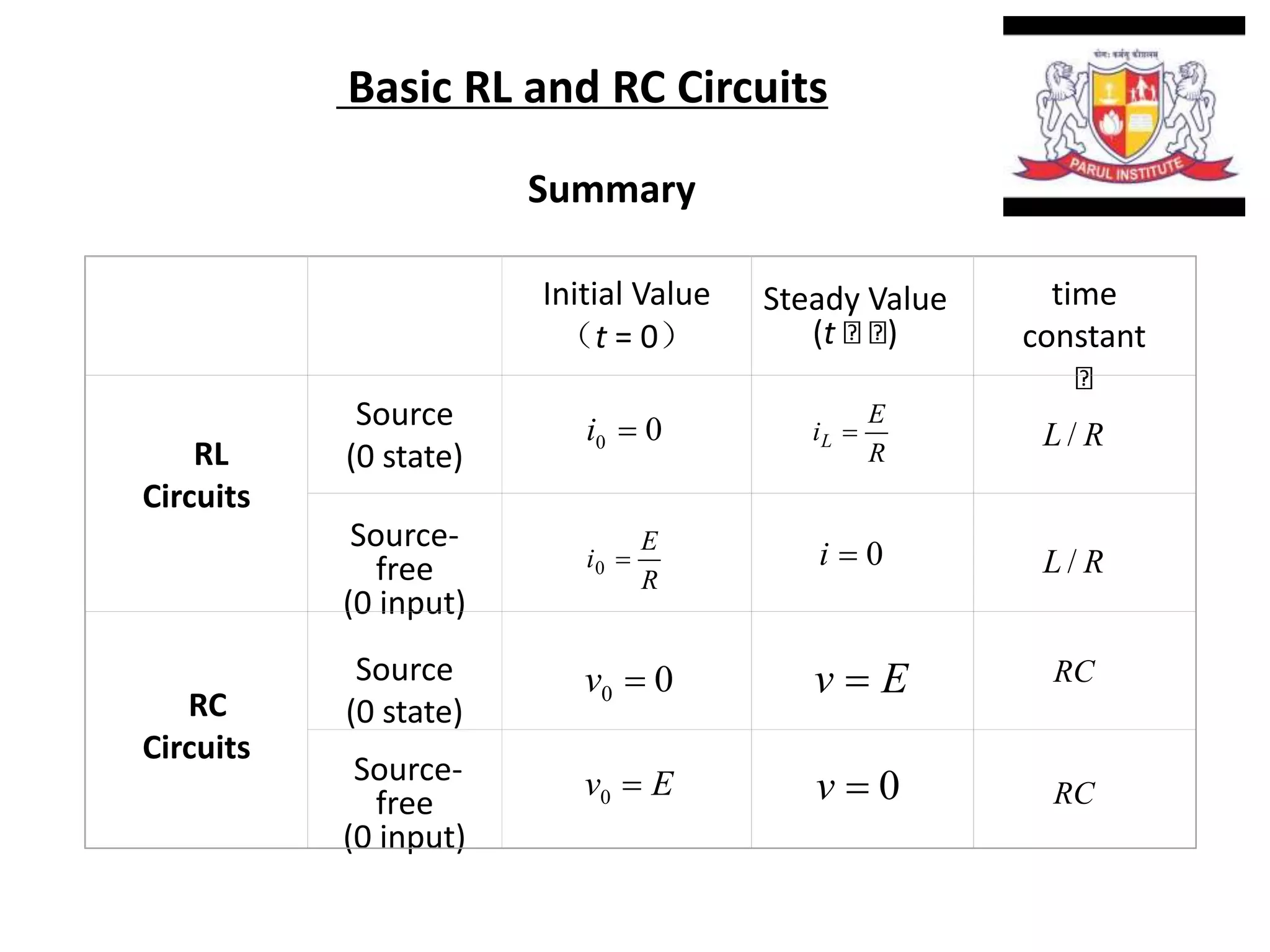
The document summarizes time domain responses in RC and RL circuits. It describes that transients are the time-varying currents and voltages resulting from sudden changes in sources. RC circuits with a single energy storage element are first-order circuits that can be used for filtering. The time constant for an RC circuit is RC and for an RL circuit is L/R. It represents the time required for an exponential to decay to 36.7% of its initial value. The document also discusses determining the initial conditions for transient analysis based on inductor current and capacitor voltage remaining constant during circuit changes.

1. Time domain response in RC &
RL circuits
By:
 Jenish Thumar -130870111038
 Dharit Unadkat -130870111039
 Shivam Rai -130870111029
Guided by:
Prof. Dipti Patel
Ec 3rd semester

2. Transients
•The time-varying currents and voltages resulting from
the sudden application of sources, usually due to
switching, are called transients.
•By writing circuit equations, we obtain
integrodifferential equations.

3. Basic RL and RC Circuits
First-Order RC Circuits
• Used for filtering signal by blocking certain frequencies and passing
others. e.g. low-pass filter
• Any circuit with a single energy storage element, an arbitrary number
of sources and an arbitrary number of resistors is a circuit of order 1.
• Any voltage or current in such a circuit is the solution to a 1st order
differential equation.
Ideal Linear Capacitor
dt
dq
ti =)(
dt
dv
c
   2
2
1
cvcvdvpdtwEnergy stored
A capacitor is an energy storage device memory device.
)(=)+( tvtv Cc

4. Basic RL and RC Circuits
First-Order RC Circuits
• One capacitor and one resistor
• The source and resistor may be equivalent to a circuit with
many resistors and sources.
R
+
-
Cvs(t)
+
-
vc(t)
+ -
vr(t)

5. Basic RL and RC Circuits
First-Order RC Circuits
)1( 
t
C eEv




/tc
e
E
dt
dv 

0
0

 
t
c
t
c
dt
dv
EE
dt
dv


RCTime Constant
R
5


1

C

2
K
E
0s 1ms 2ms 3ms 4ms
V(2)
0V
5V
10V
SEL>>
RC
R=2k
C=0.1 F

6. Basic RL and RC Circuits
First-Order RC Circuits
Switch to 2
R

1

C

2
K
E
RC
t
c Aev


Initial condition Evv CC  )0()0(
0 Riv cc
0
dt
dv
RCv c
c
// tRCt
c EeEev 

/t
c e
R
E
i 

• Transient Response of RC Circuits
c
c
dv
i C
dt


7. Series RL Circuit
dt
tdi
Ltv
tiRtv
L
L
LR
)(
*)(
)(*)(


sL
L
VtiR
dt
di
L  )(*
L
V
ti
L
R
dt
di s
L
L
 )()(
0)()(
0,For t


tvtvV LRs

8. dt
tdv
Cti
tiRtv
C
R
)(
*)(
)(*)(


sc
c
Vtv
dt
dv
CR  )(*
sc
c
V
CR
tv
CRdt
dv
)
*
1
()()
*
1
( 
0)()(  tvtvV cRs
Series RC Circuit

9. )()
1
(
)(
Ktx
dt
tdx


General First Order Differential Equation
Solution of First Order Differential Equation
determinedbetoconstantsareB,A,
0for tBeA(t) t*


x
responsenaturalthecalledisBe
responseforcedthecalledisA
t*

10. Basic RL and RC Circuits
First-Order RC Circuits
RCTime Constant
R


5
IS 

1

C

2
K
E
R=2k
C=0.1 F
Time
0s 1.0ms 2.0ms 3.0ms 4.0ms
V(2)
0V
5V
10V
SEL>>

t
RC
t
C EeEetv

)(

E
dt
dv
t
C

0
0

t
C
dt
dv
E


11. Basic RL and RC Circuits
First-Order RL Circuits
Ideal Linear Inductor
i(t) +
-
v(t)
The
rest
of
the
circuit
L
dt
di
LiivP 
)(
2
1
)( 2
tLiLidipdttwL   Energy stored:
• One inductor and one resistor
• The source and resistor may be equivalent to a circuit with many
resistors and sources.

12. Basic RL and RC Circuits
First-Order RL Circuits
Time constant
•Indicate how fast i (t) will drop to zero.
•It is the amount of time for i (t) to drop to zero if it is dropping at
the initial rate .
t
i (t)
0 
.
0t
t
dt
di

13. Basic RL and RC Circuits
First-Order RL Circuits
Switch to 2
t
L
R
Aei
dt
L
R
i
di
iR
dt
di
L



 0
Initial condition
R
E
It  0,0
/t
t
L
R
e
R
E
e
R
E
i 


Transient Response of RL Circuits
R

1

L

2
K
E
 
 
 
0
0
0
0
0
: 0
:
1
ln
i t t
I
i t t
I
t t
i I i t
R
di dt
i L
R
i t
L
 
 
  

   
 
t
L
R
I
ti

0
)(
ln
t
L
R
eIti

 0)(

14. Basic RL and RC Circuits
Initial Value
（t = 0）
Steady Value
(t )
time
constant
RL
Circuits
Source
(0 state)
Source-
free
(0 input)
RC
Circuits
Source
(0 state)
Source-
free
(0 input)
00 i
R
E
iL 
R
E
i 0 0i
00 v Ev 
Ev 0 0v
RL /
RL /
RC
RC
Summary

15. Basic RL and RC Circuits
Summary
The Time Constant
• For an RC circuit,  = RC
• For an RL circuit,  = L/R
• -1/ is the initial slope of an exponential with an initial value of 1
• Also,  is the amount of time necessary for an exponential to decay to
36.7% of its initial value

16. Basic RL and RC Circuits
Summary
•How to determine initial conditions for a transient circuit. When a sudden change
occurs, only two types of quantities will remain the same as before the change.
–IL(t), inductor current
–Vc(t), capacitor voltage
•Find these two types of the values before the change and use them as the initial
conditions of the circuit after change.

17. Thank You