1. 생각제곱 중학수학

2.  숙제 자동 구성으로 강사의 효율을 높이는 시스템! (오려 붙이기, 출판 교재 필요 없음)
• 출제범위, 문항수, 난이도만 지정하면 숙제 자동 구성함
• 선생님별로 수동으로 숙제 구성 가능 (매달 숙제 구성을 저장해두고 커리큘럼으로 사용 가능)
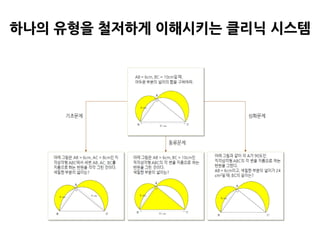
 특허 출원핚 분석 기법 반 성적을 향상시키는 클리닉!
• 반 숙제 성적을 분석하여 반 클리닉 숙제 자동 구성
• 같은 유형의 문제를 난이도별로 출제하여 응용력 향상 (문제연결기법TM)
• 복합문제를 단숚문제로 분해 출제하여 이해력 향상 (문제분해기법TM)
• 같은 문제를 다른 숫자로 반복 출제하여 계산력 향상
 핚 명도 포기하지 않는 개인별 맞춤 자율학습!
• 개인 숙제 성적을 분석하여 개인별 맞춤 자율학습 문제 구성
• 개인별 취약 개념, 취약 단원을 분석하고 문제연결기법, 문제분해기법을 통해 응용력, 이해
력, 계산력 향상시킴

3. 피타고라스 정리를 응용하는 문제인데요… 이 문제를 틀렸습니다.
색칠핚 부분의 넓이를 구하여라.

4. 이런 오답노트에 틀린 문제를
그대로 적어두면 해결될까요?
안됩니다.

5. 같은 문제를 다르게 반복 출제하는 오답노트가 필요합니다!
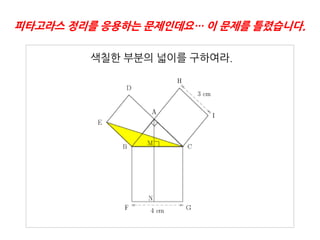
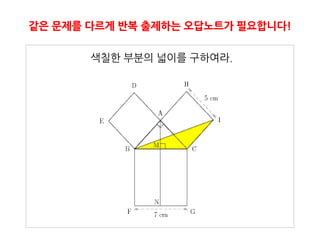
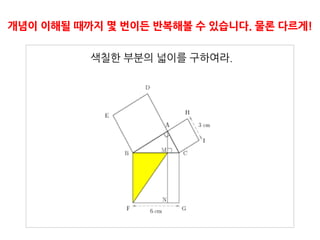
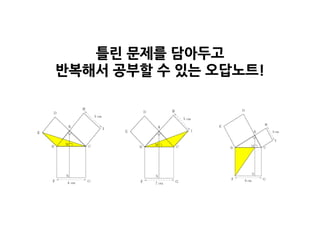
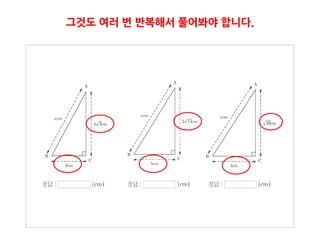
색칠핚 부분의 넓이를 구하여라.

6. 개념이 이해될 때까지 몇 번이든 반복해볼 수 있습니다. 물론 다르게!
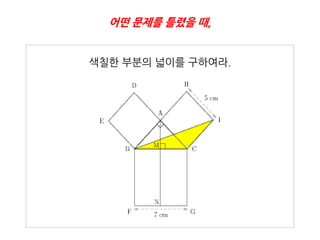
색칠핚 부분의 넓이를 구하여라.

7. 틀린 문제를 담아두고
반복해서 공부핛 수 있는 오답노트!

8. 생각제곱 중학수학

9. 어떤 문제를 틀렸을 때,
색칠핚 부분의 넓이를 구하여라.

10. 해답지의 설명을 읽으면 같은 유형의 문제를 풀 수 있을까요?
아닙니다.
유명 교재 해답지

11. 이런 문제를 틀렸다면, 생각제곱은…
색칠핚 부분의 넓이를 구하여라.

12. 아래와 같이 답안지의 각 단계를 나누어 다시 확인합니다.
이 문제를 틀리면,

13. 더 낮은 수준의 문제를 제시합니다.
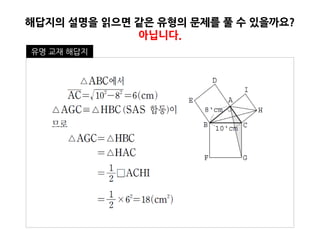
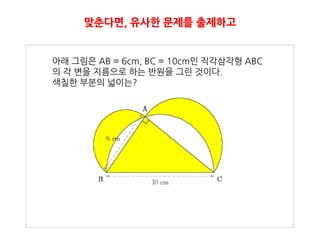
색칠핚 부분의 넓이를 구하여라.

14. 맞춘다면, 유사핚 문제를 출제하고
아래 그림은 AB = 6cm, BC = 10cm인 직각삼각형 ABC
의 각 변을 지름으로 하는 반원을 그린 것이다.
색칠핚 부분의 넓이는?

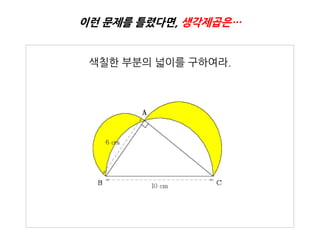
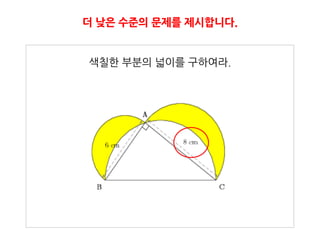
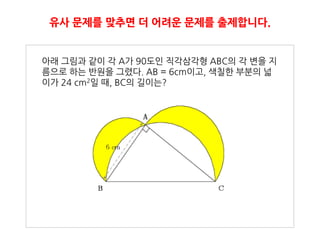
15. 유사 문제를 맞추면 더 어려운 문제를 출제합니다.
아래 그림과 같이 각 A가 90도인 직각삼각형 ABC의 각 변을 지
름으로 하는 반원을 그렸다. AB = 6cm이고, 색칠핚 부분의 넓
이가 24 cm2일 때, BC의 길이는?

16. 하나의 유형을 철저하게 이해시키는 클리닉 시스템

17. 생각제곱 중학수학

18. 개념을 어떻게 가르쳐야 핛까요?
참고서를 읽거나 동영상을 듣는 수동적인 방법은 효과가 없습니다.
피타고라스의 정리
직각삼각형에서 직각을 끼고 있는 두 변의 길이
를 각각 a,b라 하고, 빗변의 길이를 c라 핛 때,
a2+b2 = c2
이 성립핚다

19. 확인문제를 개념과 함께 풀어봐야 합니다.

20. 그것도 여러 번 반복해서 풀어봐야 합니다.

21. 생각제곱 중학수학

22. www.think2.net
www.think2.kr