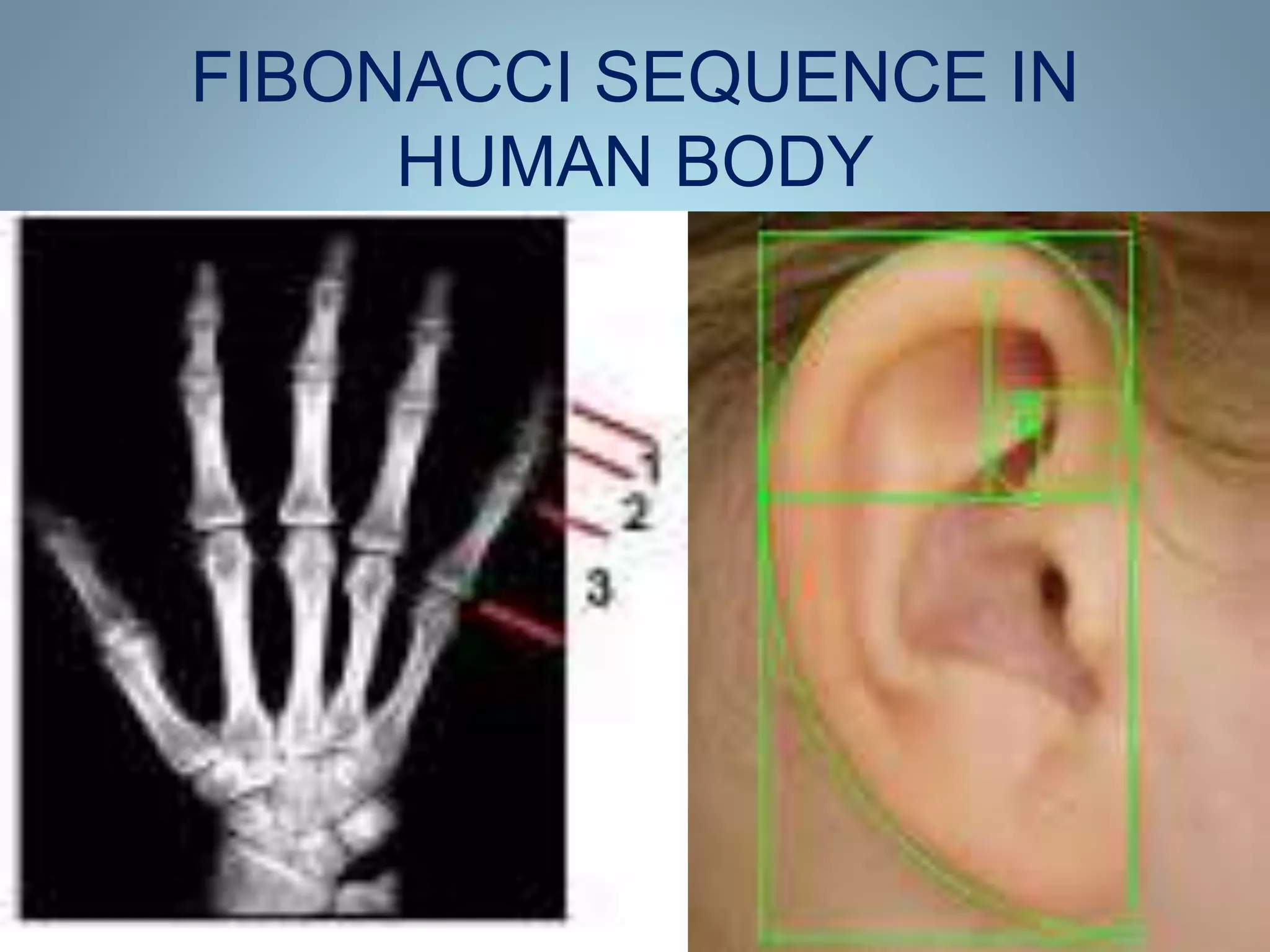
The Fibonacci sequence is a series of numbers generated by adding the two previous numbers, starting with 0 and 1, and appears in various natural patterns. Historically, the sequence's concept can be traced back to Indian mathematicians around 200 BC and was introduced to Europe by Fibonacci in 1202. The sequence manifests in petal counts of flowers, seed arrangements in sunflowers, sea shell spirals, and even human anatomy.

1. THE FIBONACCI SEQUENCE

2. What is fibonacci sequence?
• Fibonacci sequence is a series of numbers that follow
a unique integer sequence.
• These numbers generate mathematical patterns that
can be found in all aspects of life.
• The patterns can be seen in everything from the
human body to the physiology of plants and animals.
• The fibonacci sequence is derived from the fibonacci
numbers.

3. How are these fibonacci numbers
obtained?
• These numbers are obtained from the formula-
Fn=Fn-1+Fn-2
• These numbers are obtained by adding the two
previous numbers in the sequence to obtain the next
higher number.

4. HOW DOES THE FIBONACCI
SEQUENCE WORK?
• The Fibonacci sequence is as follows:
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610..and so
on.
• As a rule the first 2 numbers in the sequence has to be
0 and 1 .All other numbers follow the rule of adding
the two previous numbers in the sequence.
EXAMPLE: 1+1=2, 2+3=5, 5+3=8
• Every third number in the sequence is even.

5. What is the history of the fibonacci
sequence?
• The exact date of origin of the Fibonacci sequence is
unknown.
• It is believed that contributions to the theory began
in 200 BC by Indian mathematicians whose studies
were based in the language of Sanskrit.
• The sequence was introduced to Western European
mathematicians in 1202 by Aka Fibonacci (famous as
the Leonardo of Pisa).

6. • His study of the sequence began with the breeding
patterns of rabbits. In which, he found rabbit
generations duplicated in accordance with the
Fibonacci numbers.

7. Fibonacci rectangle
• The Fibonacci rectangle is a rectangle which is further
divided into squares whose lengths are the
consecutive numbers of the Fibonacci sequence.

8. Fibonacci spiral
• This spiral is created by drawing circular arcs connecting the opposite corners of
squares in the Fibonacci rectangle.
• The numbers form what are called as Fibonacci rectangles. These rectangles are unique
because each rectangle has length of sides equal to the magnitude of the Fibonacci
numbers.
• Within these rectangles we can create a spiral with cross sections equal to exactly
1.618 (the golden mean) with the corresponding angle of 137.5 degrees.

9. Fibonacci in nature

10. Fibonacci sequence in petal
patterns
• The Fibonacci sequence can be seen in most petal
patterns. For example, most daisies have 34,55or 89
petals and most common flowers have 5, 8 or 13 petals.

11. Fibonacci sequence in sunflowers
• The Fibonacci sequence can be found in a sunflower
heads seed arrangement .
• The arrangement of seeds corresponds to Fibonacci
spiral and they are arranged in an angle of 137.5
degrees which is also called the ‘golden angle’.

12. Fibonacci sequence in pine cones

13. Fibonacci sequence in sea shells
• The Fibonacci spiral directly correspond to the spiral
found in sea shells.

14. Fibonacci is also found in monalisa
TOO!

15. FIBONACCI SEQUENCE IN
HUMAN BODY

16. THANK YOU
-SMRUTI S SHETTY
XC , G17
Sharada Vidyalaya,
Mangalore