Downloaded 344 times
Uploaded byMaizun Azian
T2 bab 6 teorem pythagoras
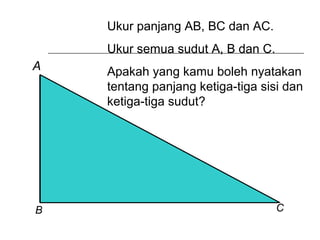
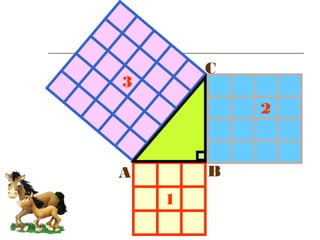
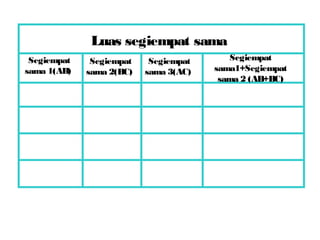
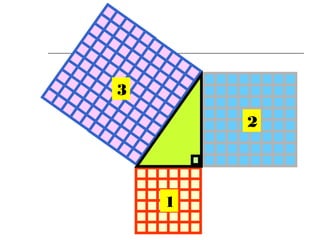
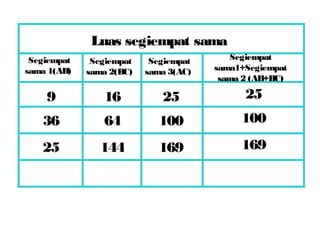
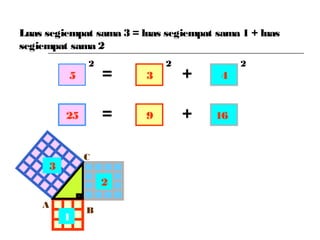
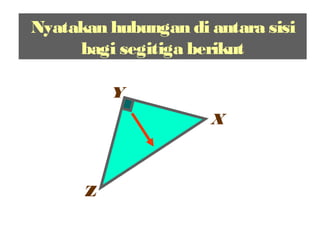
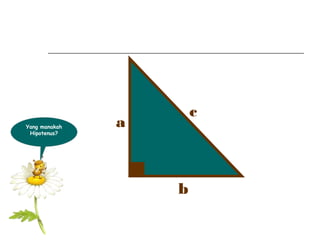
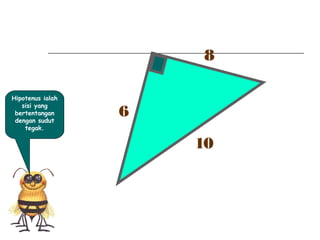
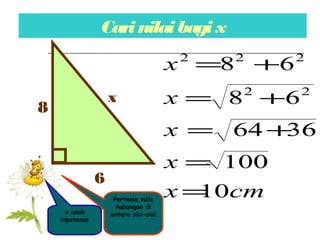
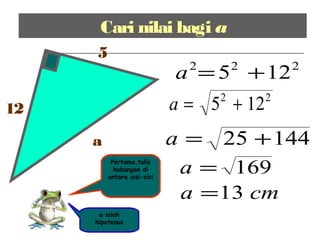
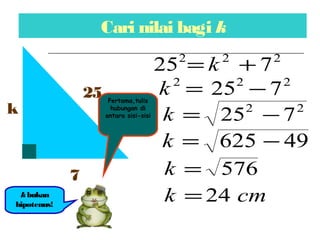
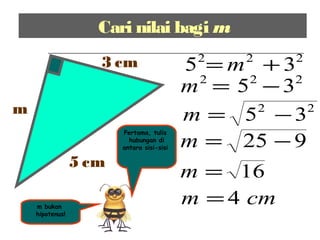
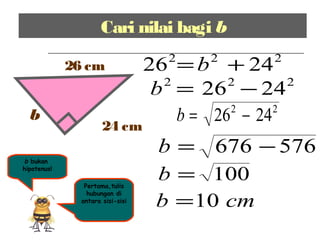
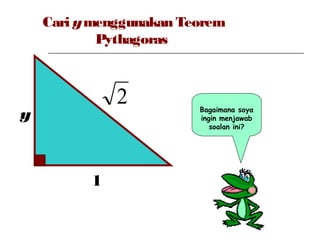
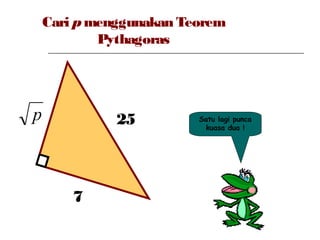
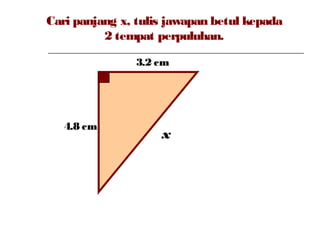
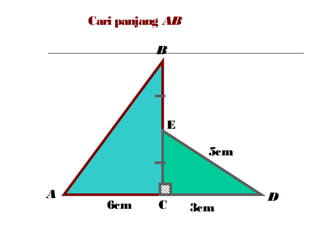
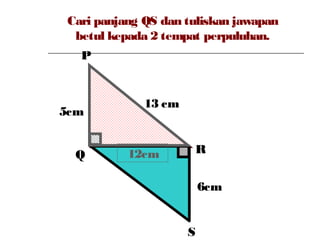
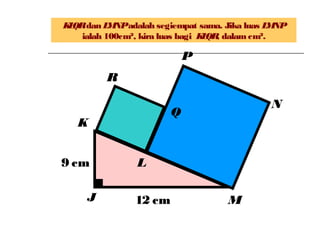
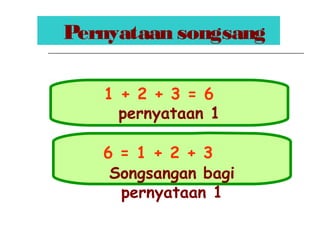
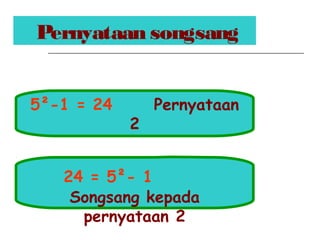
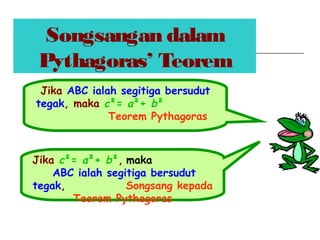
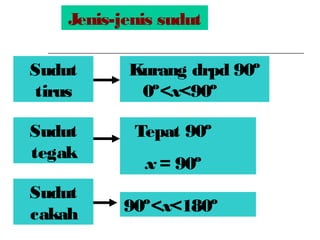
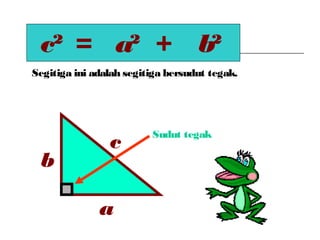
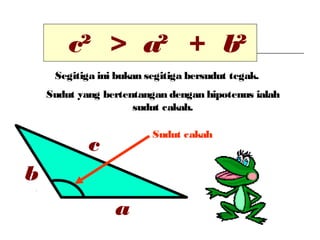
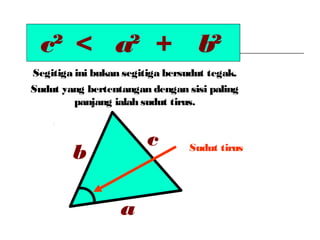
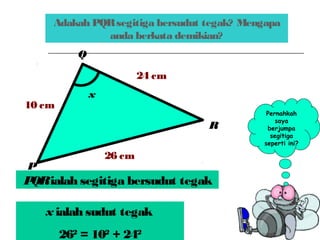
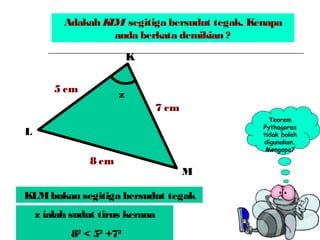
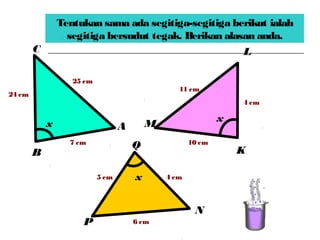
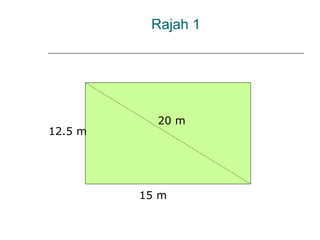
Dokumen ini membincangkan Teorem Pythagoras dan aplikasinya dalam menentukan panjang sisi segitiga bersudut tegak serta memberikan latihan berkaitan. Pembelajaran termasuk mengenal pasti hipotenus, mengukur panjang sisi, dan menyelesaikan masalah geometrik menggunakan teorem tersebut. Penggunaan teorem Pythagoras juga diterangkan untuk menentukan jenis segitiga dan sudut-sudutnya.
T2 bab 6 teorem pythagoras
- 1. MATEMATIK TINGKATAN 2 TEOREMPYTHAGORAS
- 2. Perkaitan antara sisi-sisidalam segitiga bersudut tegak Hasil pembelajaran: 1. Mengenal pasti hipotenus bagi segitiga bersudut tegak. 2. Menentukan perkaitan antara panjang sisi dalam segitiga bersudut tegak.
- 3. Ukur panjang AB,BC dan AC. Ukur semua sudut A, B dan C. Apakah yang kamu boleh nyatakan tentang panjang ketiga-tiga sisi dan ketiga-tiga sudut? A B C
- 4. Hipotenus Dalam segitiga bersudut tegak,sisi yang bertentangan dengan sudut tegak ialah hipotenus.Ia juga adalah sisi paling panjang.
- 5. Perkaitan antara panjang sisidalamsegitiga bersudut tegak.
- 6. Luas segiempat sama Denganmenghitung bilangan unit segiempat sama, cari luas yang bertanda 1, 2 dan 3.
- 7.
- 8. Guru mengedarkanbentuk segitiga bersudut tegak dengan pelbagai saiz (3,4,5; 5,12,13; 8,15,17) dan segiempat sama dengan ukuran di atas yang dipotong daripada kertas grid. Murid-murid memilih segiempat sama yang sepadan dengan sisi setiap segitiga. Murid-murid melengkapkan jadual.
- 9. Segiempat sama 1(AB) Luas segiempatsama Segiempat sama1+Segiempat sama 2 (AB+BC) Segiempat sama 2(BC) Segiempat sama 3(AC)
- 10.
- 11. Luas segiempat sama 916 25 25 36 64 100 100 25 144 169 169 Segiempat sama 1(AB) Segiempat sama 2(BC) Segiempat sama 3(AC) Segiempat sama1+Segiempat sama 2 (AB+BC)
- 12. = + = + 22 2 Luas segiempat sama 3 = luas segiempat sama 1 + luas segiempat sama 2 A B C 1 2 3 5 3 4 25 9 16
- 13. TeoremPythagoras menyatakan Dalamsegitiga bersudut tegak,kuasa dua hipotenus bersamaan dengan hasil tambah kuasa dua bagi dua sisi yang lain
- 14.
- 15. Nyatakan hubungan diantara sisi bagi segitiga berikut Z Y X XZ² =XY2 + YZ2
- 16.
- 17. 6 8 10 Hipotenus ialah sisi yang bertentangan dengansudut tegak. 10² 6² 8²+
- 18. l m k Adakah ia nampak biasa? Bolehkahkamu nyatakan hubungan di antara sisi-sisi bagi segitiga berikut?
- 19.
- 20. Carinilai bagix 6 8 x Pertama,tulis hubungan di antarasisi-sisi cmx x x x x 10 100 3664 68 68 22 222 = = += += += x ialah hipotenus
- 21. Cari nilai bagia 12 5 a a ialah hipotenus 222 125 +=a 14425 +=a 169=a cma 13= Pertama,tulis hubungan di antara sisi-sisi 22 125 +=a
- 22. Cari nilai bagik k 7 25 kbukan hipotenus! 222 725 += k 222 725 −=k 22 725 −=k 49625 −=k 576=k cmk 24= Pertama,tulis hubungan di antara sisi-sisi
- 23. Cari nilai bagim m bukan hipotenus! 222 35 += m 222 35 −=m 22 35 −=m 925 −=m 16=m cmm 4= m 3 cm 5 cm Pertama, tulis hubungan di antara sisi-sisi
- 24. Cari nilai p,betul kepada 2 t.p 7 p 15 p bukan hipotenus! 222 715 += p 222 715 −=p 22 715 −=p 49225 −=p 176=p cmp 27.13= Pertama,tulis hubungan di antara sisi-sisi
- 25. Cari nilai bagib b 26 cm 24 cm b bukan hipotenus! Pertama,tulis hubungan di antara sisi-sisi 222 2426 += b 222 2426 −=b 576676 −=b 100=b cmb 10= 22 2426 −=b
- 26. Topik Teorem Pythagoras Hasilpembelajaran: 1. Dapat mencari panjang sisi yang tidak diberi nilai dalam segitiga bersudut tegak menggunakan Teorem Pythagoras. 2. Dapat mencari panjang sisi bentuk- bentuk geometri menggunakan Teorem Pythagoras. 3. Dapat menyelesaikan masalah menggunakan Teorem Pythagoras.
- 27.
- 28. Cari panjang sisi 22 bac+= 22 acb −= 22 bca −= c is the hypotenuse a and b are the other2 sides Rumus yang diubahsuai
- 29. Cari ymenggunakan Teorem Pythagoras 2 1 yBagaimana saya ingin menjawab soalan ini?
- 30. Cari pmenggunakan Teorem Pythagoras p 7 25Satu lagi punca kuasa dua !
- 31. Cari panjang x,tulis jawapan betul kepada 2 tempat perpuluhan. 3.2 cm x 4.8 cm
- 32.
- 33. Cari panjang QSdan tuliskan jawapan betul kepada 2 tempat perpuluhan. P Q R S 6cm 5cm 13 cm 12cm
- 34. KLQRdan LMNPadalah segiempatsama. Jika luas LMNP ialah 100cm², kira luas bagi KLQR, dalamcm². L K N M P Q J R 12 cm 9 cm
- 35. Pernyataan songsang 1 +2 + 3 = 6 pernyataan 1 6 = 1 + 2 + 3 Songsangan bagi pernyataan 1
- 36. Pernyataan songsang 5²-1 =24 Pernyataan 2 24 = 5²- 1 Songsang kepada pernyataan 2
- 37. Songsangan dalam Pythagoras’ Teorem JikaABC ialah segitiga bersudut tegak, maka c²= a²+ b² Teorem Pythagoras Jika c²= a²+ b², maka ABC ialah segitiga bersudut tegak, Songsang kepada Teorem Pythagoras
- 38. Songsangan Teorem Pythagoras digunakan untuk Menentukan sama ada segitiga yang diberi adalah segitiga bersudut tegak. Menentukan jenis sudut yang bertentangan(sudut tegak,cakah atau tirus)
- 39. Jenis-jenis sudut Sudut tirus Sudut tegak Sudut cakah Kurang drpd90º 0º<x<90º Tepat 90º x = 90º 90º<x<180º
- 40. c² a² b²=+ Segitiga ini adalah segitiga bersudut tegak. c a b Sudut tegak
- 41. c² a² b²>+ Sudut yang bertentangan dengan hipotenus ialah sudut cakah. c a b Sudut cakah Segitiga ini bukan segitiga bersudut tegak.
- 42. c² a² b²<+ Sudut yang bertentangan dengan sisi paling panjang ialah sudut tirus. Sudut tirus c a b Segitiga ini bukan segitiga bersudut tegak.
- 43. Adakah PQRsegitiga bersuduttegak? Mengapa anda berkata demikian? x 24 cm 10 cm 26 cm P R Q Pernahkah saya berjumpa segitiga seperti ini? PQRialah segitiga bersudut tegak x ialah sudut tegak 262 = 102 + 242
- 44. Adakah STU segitigabersudut tegak? Kenapa anda berkata demikian? y 9 cm 4 cm 8 cm S T U Kenapa Teorem Pythagoras tidak boleh digunakan ? Apakah masalahnya? STU bukan segitiga bersudut tegak y ialah sudut cakah kerana 92 >82 +42
- 45. Adakah KLM segitigabersudut tegak. Kenapa anda berkata demikian ? z 8 cm 5 cm 7 cm K M L Teorem Pythagoras tidak boleh digunakan. Mengapa? KLMbukan segitiga bersudut tegak z ialah sudut tirus kerana 82 < 52 +72
- 46. Tentukan sama adasegitiga-segitiga berikut ialah segitiga bersudut tegak. Berikan alasan anda. x 24 cm 7 cm 25 cm A C B x 11 cm 10 cm L K M x 6 cm 5 cm 4 cm Q N P 4 cm
- 47. Latihan 1: Seorang tukangrumah ingin membuat rangka rumah.Dia ingin memastikan dinding rumah bersudut tegak antara satu sama lain. Dia membuat ukuran bagi dua bahagian dinding dan pepenjuru seperti dalam Rajah 1. Gunakan Teorem Pythagoras untuk membantunya menentukan kedua- dua dinding bersudut tegak antara satu sama lain.
- 48. Rajah 1 15 m 12.5m 20 m
- 49. Latihan 2 Sebuah rombusmempunyai pepenjuru yang panjangnya 6 cm dan 8 cm. Cari panjang sisi-sisinya.