More Related Content
PDF
ข้อสอบคณิตศาสตร์ ม.1 เทอม 1 ชุดที่ 2 PDF
เอกสารประกอบการเรียน พหุนาม ม.2 DOC
PDF
เรื่องที่ 20 ฟิสิกส์นิวเคลียร์ PDF
พลังงานสะสมในตัวเก็บประจุ PDF
เอกสารประกอบบทเรียน เรื่อง งานและพลังงาน PDF
PDF
What's hot
PDF
สนามไฟฟ้า (Electric filed) PDF
PDF
PDF
PDF
PDF
PDF
ความหนาแน่นและความดันของของไหล PDF
ข้อสอบโอลิมปิก ม.ต้น(Ijso) เรื่องพหุนามและเศษส่วนของพหุนาม PPTX
บทที่ 3 แรง และ กฎการเคลื่อนที่ของนิวตัน PDF
โครงสร้างคณิตศาสตร์ เพิ่มเติม ม.ต้น PDF
มวล แรง และกฎการเคลื่อนที่ของนิวตัน PDF
PDF
แบบทดสอบ เรื่อง สัญกรณ์วิทยาสตร์ PDF
ชุดที่ 8 การแก้โจทย์ปัญหาเกี่ยวกับสัดส่วน PDF
แบบฝึกทักษะคณิตศาสตร์เรื่องการบวกและการลบพหุนาม PDF
แบบทดสอบ เรื่อง จำนวนจริง PPTX
จำนวนเชิงซ้อนไม่ซับซ้อนอย่างที่คิด PDF
PDF
ฟิสิกส์ 5 ไฟฟ้าสถิตย์ ตอนที่ 3 DOC
Viewers also liked
PDF
DOC
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
Similar to สมดุลและสภาพยืดหยุ่น
PDF
DOCX
แบบฝึกหัดเสริม สมดุลกล.docx PDF
เอกสารประกอบ เรื่อง สภาพสมดุลและสภาพยืดหยุ่น PDF
PDF
PDF
PPT
PDF
PDF
PPS
PDF
PPT
ดงมะไฟพิทยาคม กลุ่มพรสุดา PDF
PDF
กฎการเคลื่อนที่ของนิวตัน ม4 PDF
ตะลุยโจทย์ข้อสอบ งานและพลังงาน PDF
F457c545a9ded88f18ecee47145a72c0 PDF
PDF
PDF
เรื่องที่ 8 สภาพสมดุลยืดหยุ่น DOCX
More from Chakkrawut Mueangkhon
PDF
PPT
PPT
ตัวเก็บประจุและประจุไฟฟ้า PPT
PPTX
PDF
PPT
PPT
DOC
สมดุลและสภาพยืดหยุ่น
- 1.
สภาพสมดุล
สภาพสมดุล หมายถึง การที่วัตถุอยู่นิ่งหรือเคลื่อนที่ด้วยความเร็วคงที่ โดยไม่มี
การหมุน หรือไม่มีการเปลี่ยนสภาพการเคลื่อนที่ แบ่งเป็น 2 ประเภทคือ
สมดุลสถิต หมายถึง การที่วัตถุอยู่นิ่งโดยไม่มีการหมุน
สมดุลจลน์ หมายถึง การที่วัตถุเคลื่อนที่ด้วยความเร็วคงที่โดยไม่หมุน วัตถุจะอยู่
ในสภาพ
สมดุลต้องอยู่ในเงื่อนไข 2 ข้อ คือ
ถัามีแรงหลายแรงมากระทำาร่วมกันกับเทหวัตถุชิ้นหนึ่ง และอยู่ในภาวะสมดุล
เงื่อนไขคือ
การสมดุลแบ่งออกเป็น 3 ประเภท
(ก) สมดุลต่อการเคลื่อนที่ คือ การเลื่อนสมดุล แสดงว่า
ไม่มีการเคลื่อนด้วยความเร่ง (แต่อาจจะเลื่อนเร็วคงที่ หรือนิ่ง หรือหมุนก็ได้)
(ข) สมดุลต่อการหมุน คือ การหมุนสมดุล คือ ไม่หมุนนั้นเอง
(แต่อาจจะเลื่อนด้วยความเร่ง คือ เลื่อนอย่างไรก็ได้)
(ค) สมดุลสัมบูรณ์ของวัตถุ หมายถึง วัตถุนั้นอยู่ในสมดุลต่อการเลื่อนที่ และ
สมดุลต่อการหมุน หมายความว่า แรงต่างๆ ที่กระทำาต่อวัตถุเป็นไปตามเงื่อนไข 2
ประการ คือ
1. แรงลัพธ์เป็นศูนย์ หรือผลรวมของแรงทุกแรงที่กระทำาต่อวัตถุเป็นศูนย์
2. ผลรวมของโมเมนต์ของแรงทุกแรงที่กระทำาต่อวัตถุเป็นศูนย์
หมายเหตุ ถ้าแรงหลายแรงกระทำาต่ออนุภาค (ย่อมไม่มโมเมนต์อยู่แล้ว)
ี
เพียง อย่างเดียวก็สมดุลได้
นำำาหนักของวัตถุทำาให้เกิดแรงกดที่พืำนและแรงดึงที่เชือก
F T = แรงที่เชือกดึงวัตถุ
N F = แรงที่วัตถุดึงเชือก
W = mg
รูป ก แสดงแรงปฏิกิริยาที่พื้น (N) W = mg รูป ข
แสดงแรงดึงเชือก
@ จากรูป ก นำ้าหนักของวัตถุทำาให้เกิดแรงกดที่พื้น(F) ซึ่งมีขนาดค่าเท่ากับนำ้าหนัก
ของวัตถุ จากกฎข้อที่ 3 ของนิวตัน จึงมีแรงปฏิกิริยาที่พื้นกระทำาต่อวัตถุ(N) ซึ่งมีขนาด
เท่ากับแรงที่วัตถุกดลงบนพื้น ซึ่งจะมีทิศตั้งฉากกับพื้นเสมอ
ดังนั้นจะได้ N = -W
@ จากรูป ข แขวนวัตถุด้วยเส้นเชือกเบา นำ้าหนักของวัตถุทำาให้เกิดแรงที่วัตถุดึง
เชือก(F) ซึ่งมีขนาดเท่ากับนำ้าหนัก จากกฎข้อที่ 3 ของนิวตันจึงมีแรงปฏิกิริยาที่เชือกดึง
วัตถุ(T) เราเรียกว่าแรงดึงเชือก ซึ่งมีทิศออกจากวัตถุเสมอ
- 2.
ดังนั้นจะได้ T = -W
แรงเสียดทาน
เป็นแรงที่กระทำาในทิศต้านการเคลื่อนที่ของวัตถุเกิดขึ้นที่ผิวสัมผัสระหว่างวัตถุ 2
อัน แบ่งเป็น 2 ประเภทคือ
1. แรงเสียดทานสถิต (fS) เป็นแรงเสียดทานขณะวัตถุอยู่นิ่ง
2. แรงเสียดทานจลน์ (fK) เป็นแรงเสียดทานขณะวัตถุเคลื่อนที่
F f
N
W = mg
พิจารณากล่องที่วางบนโต๊ะ ดังรูป ถ้าออกแรง F ในแนวระดับ กระทำาต่อกล่อง
แล้วกล่องยังคงอยู่นิ่ง ถ้าแรง F ไม่มากพอ เราจะได้ว่า fS = F ถ้าออกแรงกระทำาจน
กระทั่งกล่องเริ่มจะเคลื่อนที่แรงเสียดทานจะมีค่ามากที่สุด F = fS max เมื่อกล่อง
เคลื่อนที่ไปทางขวาด้วยความเร่งแรงเสียดทานจะมีค่าลดน้อยกว่า แรงเสียดทานขณะ
วัตถุเริ่มเคลื่อนที่
จากการทดลองสำาหรับวัตถุคู่หนึ่งๆ แรงเสียดทานสถิต (fS) แรงเสียดทานจลน์
(fK) เป็นมีค่าแปรผันตรงกับแรงปฏิกิริยาที่พื้นกระทำาต่อวัตถุ(N) ซึ่งมีขนาดเท่ากับนำ้า
หนักของวัตถุที่กดลงบนพื้น ซึ่งเขียนความสัมพันธ์ได้ดังนี้
f α N
หรือ f = µN
เมื่อ f = แรงเสียดทาน
แ = สัมประสิทธิ์ความเสียดทาน
แบบฝึกหัด
1. จากรูปจงเขียนแนวแรง ของนำ้าหนัก แรงปฏิกิริยาที่พื้นกระทำากับวัตถุ และแรงเสียด
ทานที่กระทำากับวัตถุ
F F เชือก
- 3.
2. วัตถุมวล 2กิโลกรัมวางอยู่บนพื้นแรงปฏิกิริยาที่พื้นกระต่อวัตถุเป็น
เท่าใด……………………….
3. วัตถุ มวล 5 กิโลกรัมถูกแขวนด้วยเชือกติดกับบนเพดานแรงดึงในเส้นเชือกเป็น
เท่าใด………………
4. ออกแรงขนาด 20 นิวตันลากวัตถุมวล 5 กิโลกรัมไปตามพื้นราบ ถ้าสัมประสิทธิ์ความ
เสียดทานระหว่างพื้นกับวัตถุเท่ากับ 0.2
แรงเสียดทานที่พื้นกระทำากับวัตถุมีค่าเท่าใด
…………………………………………………………………………………………………………
…………………………..
…………………………………………………………………………………………………………
…………………………..
5. ต้องออกแรงลากวัตถุมวล 10 กิโลกรัมไปตามพื้นราบด้วยแรงอย่างน้อยเท่าใดวัตถุ
จึงจะเคลื่อนที่ ถ้าสัมประสิทธิ์ความเสียดทานระหว่างพื้นกับวัตถุเท่ากับ 0.2
…………………………………………………………………………………………………………
…………………………..
…………………………………………………………………………………………………………
…………………………..
6. ถ้าออกแรงขนาด 20 นิวตันลากวัตถุไปตามพื้นราบด้วยความเร็ว ถ้าสัมประสิทธิ์
ความเสียดทานระหว่างพื้นกับวัตถุเท่ากับ 0.3 วัตถุนี้มีมวลเท่าใด
…………………………………………………………………………………………………………
…………………………..
…………………………………………………………………………………………………………
…………………………..
7. แดงใช้เชือกต้องการลากวัตถุมวล 20 กิโลกรัมให้เคลื่อนที่ไปตามแนวราบ ในทิศทำา
มุมกับแนวระดับ 37 องศา แดงต้องออกแรงอย่างน้อยเท่าใดจึงจะลากให้วัตถุนี้
เคลื่อนที่ได้ (ประสัมประสิทธิ์ความเสียดทานระหว่างพื้นกับวัตถุเท่ากับ 0.4 )
…………………………………………………………………………………………………………
…………………………..
…………………………………………………………………………………………………………
…………………………..
8. วัตถุมวล 10 กิโลกรัมวางนิ่งอยู่บนพื้นเอียง ซึ่งทำามุม 53 องศากับแนวระดับ จง
ขนาดของแรงเสียดทาน และสัมประสิทธิ์ความเสียดทานของพื้นกับวัตถุ
…………………………………………………………………………………………………………
…………………………..
…………………………………………………………………………………………………………
…………………………..
เงื่อนไขข้อที่ 1 ของสภาพสมดุล
วัตถุจะอยู่ในสภาพสมดุลได้โดยไม่เปลี่ยนสภาพการเคลื่อนที่ ก็ต่อเมื่อ ผลรวม
ของแรงกระทำาในแนว X และ Y เป็นศูนย์ ( กฎข้อที่ 1 ของนิวตัน )
หลักในการคำานวณสมดุลโดยใช้เงื่อนไขข้อที่ 1
1. ตั้งแกน X และแกน Y ที่จุดตัดของแนวแรงแต่ละแรง
- 4.
2. แตกแรงแต่ละแรงให้อยู่ในแนวแกน Xและแกน Y
3. รวมแรงแต่ละแนวแบบเวกเตอร์ โดยใช้สมการ
- ∑FX = 0 ( แรงรวมขวา = แรงรวมซ้าย )
- ∑FY = 0 ( แรงรวมบน = แรงรวมล่าง )
4. แก้สมการหาค่าตัวแปร
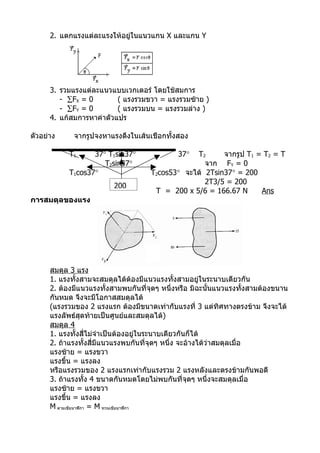
ตัวอย่าง จากรูปจงหาแรงดึงในเส้นเชือกทั้งสอง
T1 37° T1sin37° 37° T2 จากรูป T1 = T2 = T
T2sin37° จาก FY = 0
T1cos37° T2cos53° จะได้ 2Tsin37° = 200
2T3/5 = 200
200
T = 200 x 5/6 = 166.67 N Ans
การสมดุลของแรง
สมดุล 3 แรง
1. แรงทั้งสามจะสมดุลได้ต้องมีแนวแรงทั้งสามอยู่ในระนาบเดียวกัน
2. ต้องมีแนวแรงทั้งสามพบกันที่จุดๆ หนึ่งหรือ มิฉะนั้นแนวแรงทั้งสามต้องขนาน
กันหมด จึงจะมีโอกาสสมดุลได้
(แรงรวมของ 2 แรงแรก ต้องมีขนาดเท่ากับแรงที่ 3 แต่ทิศทางตรงข้าม จึงจะได้
แรงลัพธ์สุดท้ายเป็นศูนย์และสมดุลได้)
สมดุล 4
1. แรงทั้งสีไม่จำาเป็นต้องอยู่ในระนาบเดียวกันก็ได้
่
2. ถ้าแรงทั้งสี่มีแนวแรงพบกันที่จุดๆ หนึ่ง จะอ้างได้ว่าสมดุลเมื่อ
แรงซ้าย = แรงขวา
แรงขึ้น = แรงลง
หรือแรงรวมของ 2 แรงแรกเท่ากับแรงรวม 2 แรงหลังและตรงข้ามกันพอดี
3. ถ้าแรงทั้ง 4 ขนาดกันหมดโดยไม่พบกันที่จุดๆ หนึ่งจะสมดุลเมื่อ
แรงซ้าย = แรงขวา
แรงขึ้น = แรงลง
M ตามเข็มนาฬิกา = M ทวนเข็มนาฬิกา
- 5.
ทฤษฎีลามี (กฎของ sine)
แรง3 แรงมากระทำากันที่จุด ๆ หนึ่ง และอยู่ในภาวะสมดุล อัตราส่วนของแรงต่อ sin
ของมุมตรงข้ามย่อมมีค่าเท่ากัน
สามเหลี่ยมแทนแรง
ถ้ามีแรง 3 แรงกระทำาร่วมกันที่จุด ๆ หนึ่ง และอยู่ในภาวะสมดุลโดยทิศของแรงทั้ง 3
แรงตั้งฉากกับด้านทั้ง 3 ของสามเหลี่ยม
จะได้อัตราส่วนขนาดของแรงต่อด้านที่แรงนั้นตั้งฉากอยู่
1. วัตถุในรูปที่กำาหนดให้มีนำ้าหนัก W อยูในสภาพสมดุล จงหา T1 และ T2
่
ถ้า 1 = 53° , θ2 = 37° และ W = 60 นิวตัน
T2 T1
θ1 θ2
2. นำ้าหนัก W1 ในรูปที่กำาหนดให้เท่ากับ 300 นิวตัน จงหา T1 , T2 ,T3 และ
W2
T3 T1
53° 37°
- 6.
T2
W2 W1
3. จากรูปที่กำาหนดให้
100 N
50 N
จงหา
1. แรงเสียดทานที่น้อยที่สุดทีทำาให้ระบบสมดุล
่
2. สัมประสิทธิ์ความเสียดทานระหว่างแรง 100 นิวตันกับพื้นโต๊ะ
ในข้อ ก มีค่าเท่าใด
3. ถ้าสัมประสิทธิ์ความเสียดทานระหว่างกล่อง 100 นิวตัน กับ
พื้นโต๊ะเท่ากับ 0.25 จงหาว่านำ้าหนักที่จะมาแทนนำ้าหนัก 50
นิวตัน เพื่อให้สมดุลมีค่าเท่าใด
1.เมื่อมีแรงสองแรงมากระทำาต่อวัตถุ ปรากฏว่าวัตถุอยู่ในสภาพสมดุล ข้อความใดกล่าว
ถูกต้อง
ก. แรงทั้งสองต้องมีขนาดเท่ากัน แต่ทิศทางตรงข้ามกัน ข. แรงทั้งสองต้อง
อยู่ในแนวเส้นตรงเดียวกัน
ค. แรงทั้งสองต้องอยู่ในระนาบเดียวกัน ง. ถูกทั้งข้อ 1,2 และ 3
2. เมื่อมีแรงสามแรงซึ่งไม่อยู่ในแนวเดียวกันกระทำาต่อวัตถุ แล้ววัตถุอยู่ในสภาพสมดุล
ข้อความใดกล่าวถูกต้อง
ก. แนวแรงทั้งสามต้องพบกันที่จุด ๆ หนึ่ง ข. แรงทั้งสามต้องอยู่ใน
ระนาบเดียวกัน
ค. ผลรวมของแรงคู่ใดคู่หนึ่งจะมีขนาดเท่ากับแรงที่สาม แต่มีทิศทางตรงข้ามกัน ง.
ถูกทั้งข้อ 1, 2 และ 3
3. เมื่อมีแรงมากกว่าสามแรง กระทำาต่อวัตถุ ปรากฏว่าวัตถุอยู่ในสภาพสมดุล ข้อความ
ใดกล่าวถูกต้อ
ก. แรงเหล่านันต้องพบกันที่จุด ๆ หนึ่ง
้ ก. แรงเหล่านันต้องอยู่ใน
้
ระนาบเดียวกัน
ค. เมื่อหาแรงลัพธ์โดยการวาดรูปจะได้รูปปิดพอดี ง. ถูกทั้งข้อ 1, 2 และ 3
- 7.
4. ขนาดของแรงชุดใดต่อไปนี้ที่ให้วัตถุอยู่ในสภาพสมดุล เมื่อแรงทุกแรงอยู่ในระนาบ
เดียวกัน
ก.5, 10 และ 20 นิวตัน ข. 10, 10 และ 10 นิวตัน ค. 15, 15 และ 35 นิวตัน
ง. 10 , 30 50 นิวตัน
5. โคมไฟมวล 8.5 กิโลกรัม ห้อยอยู่ด้วยลวดเบาสองเส้นดังรูป จงหาความตึงในเส้น
ลวดทั้งสอง กำาหนดให้ sin 10o = 0.17, cos 10o = 0.98
ก. 250 นิวตัน ข. 500 นิวตัน ค. 600 นิวตัน ง. 850
นิวตัน
6. แขวนวัตถุหนัก W ไว้ที่ปลายของเชือกสองเส้น แรงตึงในเส้นเชือกจะเป็นอย่างไร
ก. เชือกแต่ละเส้นตึง W/2 ข. ผลรวมแบบเวกเตอร์ของแรงตึงเชือก
ทั้งสองมีขนาดมากกว่า W
ค. ผลรวมแบบเวกเตอร์ของแรงตึงเชือกทั้งสองมีขนาดเท่ากับ W ง. เชือก
แต่ละเส้นตึง W
7.จากรูป m1 = 20 กิโลกรัม, m2 = 15 กิโลกรัม รอกเบาและลื่นระบบอยู่ในสภาพสมดุล
มุม มีค่าเท่าไร
ก. 30 องศา ข. 37 องศา
ค. 45 องศา ง. 53 องศา
สมดุลต่อการหมุน
เมื่อมีแรงเดี่ยวหรือแรงลัพธ์กระทำาต่อวัตถุที่อยู่นิ่งโดยแนวแรงไม่ผ่านศูนย์กลาง
มวลจะทำาให้วัตถุนั้นหมุน
ตัวอย่างการหมุนที่พบเห็นในชีวิตประจำาวัน เช่น
การปั่นจักรยาน การเปิดประตู การเปิดฝาขวดที่เป็นฝาเกลียว ฯลฯ
แรงขนาน คือ แรงที่กระทำาต่อวัตถุเดี่ยวกันโดยมีแนวแรงขนานกัน
แรงคู่ควบ คือ แรงขนานที่มีขนาดเท่ากันกระทำาต่อวัตถุเดี่ยวกันในทิศทางตรง
ข้ามกัน
โมเมนต์ของแรง คือ ผลคูณระหว่างขนาดของแรงกับระยะทางจากจุดหมุนไปตั้ง
ฉากกับแนวแรง
M = FL
โมเมนต์ของแรงมีหน่วยเป็น นิวตัน เมตร
การหมุนของวัตถุในระนาบหนึ่งๆเมื่อพิจารณาเทียบกับการหมุนของนาฬิกาจะเห็นว่ามี
ทิศทางการหมุนได้สองแบบ คือ
1. การหมุนตามเข็มนาฬิกา
2. การหมุนทวนเข็มนาฬิกา
ดังนั้นจึงได้ว่า
- 8.
โมเมนต์ตามเข็มนาฬิกา คือ โมเมนต์ของแรงที่กระทำาให้วัตถุหมุนในทิศทางตามเข็ม
นาฬิกา
โมเมนต์ทวนเข็มนาฬิกา คือ โมเมนต์ของแรงที่กระทำาให้วัตถุหมุน
โมเมนต์ของแรงที่กระทำาให้วัตถุหมุนในทิศทางทวนเข็มนาฬิกา
วัตถุที่อยู่ในสภาพสมดุลต่อการหมุน โมเมนต์ของแรงที่กระทำาต่อวัตถุเป็นไปตาม
เงื่อนไข คือ
โมเมนต์ทวนเข็มนาฬิกา = โมเมนต์ตามเข็มนาฬิกา
F1L1 = F2L2
ถ้ากำาหนดให้ โมเมนต์ทวนเข็มนาฬิกามีเครื่องหมายบวก และ โมเมนต์ตามเข็ม
นาฬิกามีเครื่องหมายลบ จะได้ว่า ผลรวมทางคณิตศาสตร์ของโมเมนต์มีค่าเป็นศูนย์
โมเมนต์ของแรงคู่ควบใดๆมีขนาดเท่ากับผลคูณของขนาดของแรงกับระยะทางตั้ง
ฉากระหว่างแนวแรงทั้งสอง
ตัวอย่าง จงหาขนาดโมเมนต์ของแรงคู่ควบที่ที่กระทำาต่อวัตถุ ดังรูป และบอก
ด้วยว่าวัตถุจะหมุนอย่างไร
3 cm 100 N
١٠٠ N
วิธีทำา จากโจทย์ ระยะทางตั้งฉากระหว่างแนวแรงทั้งสอง
L = 3 cm = 3x 10 - 2 m F = 100 N
ดังนัน โมเมนต์ของแรงคู่ควบ
้
= F x L
= 100 N x 3 x 10 -2 m
= 3 N.m
จะเห็นว่าแรง 100 N ทางซ้ายและขวามือทำาให้วัตถุหมุนทวนเข็มนาฬิกา ดัง
นั้น โมเมนต์ของแรงคู่ควบ ทำาให้วัตถุหมุนทวนเข็มนาฬิกา
1. สมดุลเสถียร คือ เป็นการสมดุลของวัตถุ ซึงถ้าออกแรงกระทำาต่อวัตถุให้ขยับไปจากสมดุล
่
แล้ว เมื่อสิ้นสุดแรงกระทำา วัตถุนั้นจะกลับมาสู่สมดุลเดิมได้
รูป ก. เมื่อออกแรงผลักวัตถุให้เอียงจากสมดุลเดิม C.M. ของวัตถุจะสูงขึ้น และแนวแรง N กับ
นำ้าหนัก W จะไม่ตรงกัน จึงเกิดโมเมนต์ของนำ้าหนัก W รอบจุดรองรับ ในทิศที่ทำาให้วัตถุหมุน
กลับมาตั้งในลักษณะเดิม
2. สมดุลสะเทิน คือ เป็นการสมดุลที่วัตถุไม่กลับสู่สมดุลเดิมและไม่เคลื่อนที่ต่อไปหลังจากสิ้น
สุดแรงกระทำา
- 9.
รูป ข. เมื่อวัตถุเคลื่อนที่ไปจากสมดุลเดิมC.M. สูงเท่าเดิม และแรง N กับ
นำ้าหนัก W ยังอยู่ในแนวเดียวกันเมื่อสิ้นสุดแรงกระทำา วัตถุจะอยู่ใน
ลักษณะนั้นโดยไม่มีโมเมนต์ของแรงใดมาทำาให้หมุนอีกต่อไป
3. สมดุลไม่เสถียร คือ เป็นการสมดุลที่เมื่อวัตถุขยับจากสมดุลเดิมแล้ววัตถุจะไปอยู่ใน
ตำาแหน่งอื่น โดยไม่กลับสู่สมดุลเดิมอีก
รูป ค. เมื่อผลักวัตถุให้เคลื่อนจากสมดุลเดิมทำาให้จุด C.M. ของวัตถุตำ่ากว่าเดิม และแนวแรง N
กับ W ไม่ตรงกัน จะเกิดโมเมนต์ของนำ้าหนัก W ไม่ล้มตำ่าลงมาอีก
1. จงหาขนาดของแรงต้านของตะปู ถ้ามันจะเริ่มหลุดเมื่อถูกแรงดึงจาก
แรงในแนวราบ 400 นิวตัน ที่กระทำาต่อปลายไม้งัดดังรูป
400 N
100 mm
20 mm
2. จากรูปจงหาขนาดโมเมนต์ของแรงคู่ควบที่ที่กระทำาต่อวัตถุ ดังรูป และบอกด้วยว่า
วัตถุจะหมุนอย่างไร
100 N
20 cm 100 N
3. พวงมาลัยรถยนต์มีเส้นผ่านศูนย์กลาง 40 เซนติเมตร จงหาโมเมนต์ของแรงเมื่อใน
มือข้างเดียวและใช้มือสองข้างหมุนพวงมาลัย
4. คานสมำ่าเสมอหนัก 40 นิวตัน จงหาค่านำ้าหนัก W ที่มากที่สุดที่ทำาให้คานยังคง
วางตัวในแนวระดับได้
1. 40 นิวตัน
2. 60 นิวตัน
3. 80 นิวตัน
4. 100 นิวตัน
5. คานสมำ่าเสมอ AB ยาว 4 เมตร มีมวล 60 กิโลกรัม วางพาดอยู่บนเสา A และเสา C
ซึ่งอยู่ห่างกัน 3 เมตร ชายคนหนึ่งมีมวล 75 กิโลกรัม เดินจาก A ไป B ดังรูป จงหาว่า
เขาจะเดินได้ไกลจาก A มากที่สุดเท่าไร คานจึงคงสภาพสมดุลอยู่ได้
1. 3.2 เมตร
2. 3.4 เมตร
3. 3.6 เมตร
4. 3.8 เมตร
ข้อมูลต่อไปนี้สำาหรับโจทย์ข้อ 6 ถึง 9
บันไดหนัก 50 กิโลกรัม ยาว 10 เมตร วางพิงกำาแพงเกลี้ยงและพื้นราบขรุขระโดยปลาย
ล่างห่างจากกำาแพง 8 เมตร ปรากฏว่าบันไดพอดีจะไถล
- 10.
6. จงหาแรงปฏิกิริยาที่กำาแพง
ก. 333.33นิวตัน ข. 300 นิวตัน ค. 555.56 นิวตัน ง.
666.67 นิวตัน
7. จงหาแรงปฏิกิริยาที่พื้น
ก. 200 นิวตัน ข. 300 นิวตัน ค. 400 นิวตัน ง. 500
นิวตัน
8. สัมประสิทธิ์ของความเสียดทานระหว่างบันไดกับพื้น
ก. 0.33 ข. 0.50 ค. 0.67 ง. 0.75
9. บานพับ A และ B ยึดหน้าต่างหนัก 300 นิวตัน บานพับ A รับนำ้าหนักหน้าต่าง 2/3
ของนำ้าหนักทั้งหมด จงหาขนาดของแรงที่บานพับ A กระทำาต่อหน้าต่าง ถ้าความกว้าง
ของหน้าต่าง 0.8 เมตร และบานพับทั้งสองห่างกัน 1.0 เมตร
1. 182.4 นิวตัน
2. 233.2 นิวตัน
3. 296.6 นิวตัน
4. 344.8 นิวตัน
สภาพยืดหยุ่นของของแข็ง ความเค้นและความเครียด
สถานะของสาร มี 3 สถานะ คือ ของแข็ง ของเหลว และก๊าซ
สภาพยืดหยุ่นของของแข็ง เป็นสมบัติของของแข็งที่มีการเปลี่ยนแปลงรูปร่างเมื่อมี
แรงมากระทำา แบ่งออกเป็น 2 ประเภท คือ 1. สภาพยืดหยุ่น (elasticity)
คือสมบัติของวัสดุที่มีการเปลี่ยนแปลงรูปร่าง เมื่อมีแรงมากระทำาและสามารถคืนตัวกลับ
สู่รูปร่างเดิม เมื่อหยุดออกแรงกระทำา A 2. สภาพพลาสติก (plasticity) คือ กรณี
วัสดุเปลี่ยนรูปร่างไปอย่างถาวร โดยผิววัสดุไม่มีการฉีกขาดหรือแตกหัก
จากการดึงสปริงให้ยืดออก จะพบว่ากราฟระหว่างขนาดของแรงดึงกับความยาวที่สปริง
ยืดออก จะมีลักษณะดังรูป
จุด a คือ ขีดจำากัดการแปรผันตรง
(Proportional limit) ซึ่งเป็นตำาแหน่งสุดท้ายที่ความยาว
สปริงยืดออก แปรผันตรงกับขนาดของแรงดึง
จุด b คือขีดจำากัดสภาพยืดหยุ่น (Elastic limit)
ซึ่งเป็นตำาแหน่งสุดท้ายที่สปริงยืดออกแล้วกลับสู่สภาพเดิม
แต่แรงดึงไม่แปรผันตรงกับระยะยืด
จุด C คือ จุดแตกหัก (Breaking point) หมายถึง
ตั้งแต่จุด b เป็นต้นไป ถ้าดึงต่อไปก็ถึงจุด c ซึ่งเป็นจุดที่เส้น
วัสดุขาด
ความเค้น (Stress) s = F/A
เมื่อออกแรงกระทำาต่อวัตถุ อัตราส่วนระหว่างแรงกระทำา (F) ต่อ
พื้นที่ (A) เรียกว่า ความเค้น มีหน่วยในระบบเอสไอ เป็น นิวตัน ต่อ ตารางเมตร
- 11.
ความเค้นเป็นปริมาณสเกลาร์ โดยทั่วไปความเค้น มี2 ชนิด ได้แก่ ความเค้นตามยาว
และความเค้นเฉือน
ความเค้นตามยาว (longitudinal stress) แบ่งได้ 2 ชนิด
คือ ความเค้นแบบดึง (tensile stress) ซึงแรง F กระทำาต่อวัตถุ
่
ในลักษณะดึงให้ยืดออก กับความเค้นแบบอัด (compressive
stress) ซึ่งแรง F กระทำาต่อวัตถุในลักษณะอัดได้หดสั้นลง
ส่วนความเค้นเฉือน (shear stress) นั้น แรง F ที่กระทำาต่อวัตถุจะทำา
ให้วัตถุบิดเบือนรูปร่างไปจากเดิม
ความเครียด (Strain)
หมายถึงอัตราส่วนระหว่างรูปร่างที่เปลี่ยนไปต่อรูปร่างเดิม มีหน่วยเป็นเท่า หรือไม่มี
∆L
ε=
L0
หน่วย
ความสัมพันธ์ระหว่างความเค้นและความเครียด
เมื่อออกแรงดึงเส้นวัสดุโดยไม่ให้ขนาดของแรงดึงเกินขีดจำากัดการแปรผันตรงของวัสดุ ความเค้นตามยาวจะ
แปรผันตรงกับความเครียดตามยาว
ความเค้น (Stress) คืออัตราส่วนระหว่างแรงทั้งหมดที่กระทำาต่อผิววัตถุกับพื้นที่ผิววัตถุ
ความเครียด (Strain) คืออัตราส่วนระหว่างความยาวที่เปลี่ยนแปลงต่อความยาวเดิม (ไม่มีหน่วย) เช่น ความเครียดเส้น
ตรง
ความเครียดดึง ( tensile strain ) คือ อัตราส่วนระหว่างความยาวที่เพิ่มต่อความยาวเดิม
ความเครียดเฉือน ( shearing strain ) คือ อัตราส่วนของระยะกระจัด x ทีเปลี่ยนไปต่อความยาวเดิมทางด้านขวาง h
่
นั่นคือ ความเครียดเฉือน = x / h = tan q
มอดูลัสของความยืดหยุ่น (Modulus of Elasticity) เป็นสมบัติอย่างหนึ่งของสาร ซึ่งเป็นอัตรา ส่วนระหว่าง
ความเค้นกับความเครียด
มอดูลัสของความยืดหยุ่น = ความเค้น
ความเครียด
มอดูลัสของยัง(Young's Modulus) เป็นอัตราส่วนระหว่างความเค้นและความเครียดตามยาว (บางทีเรียกว่า สัมประสิทธิ์
ความยืดหยุ่นตรง)
กฎของฮุก ( Hooke's Law)
"ความเค้นเป็นสัดส่วนกับความเครียด"
จากกราฟ จะได้เส้นกราฟช่วง oa เป็นการยืดของ
วัสดุเป็นไปตามกฎของฮุก เมือหยุดออกแรงกระทำา
่
สปริงจะหดกลับสู่รูปร่างเดิม
- 12.
จากจุด a ถึงb ความเค้นไม่เป็นสัดส่วนกับความเครียด ใน
บริเวณ ob เป็นช่วงยังยืดหยุ่นและเรียกตรงจุด b ว่า ขีด
จำากัดสภาพยืดหยุ่น
ถ้าวัสดุยังคงถูกแรงดึงต่อไป เลย จุด b ความเครียดจะเพิ่ม
ขึ้นอย่างรวดเร็ว เมือยกเลิกแรง วัสดุจะไม่หดกลับมาเท่า
่
รูปร่างเดิม ถ้าดึงต่อไปถึงจุด c ทำาให้เกิดความเครียดมาก
จนถึงจุดแตกหัก (fracture point) วัสดุนั้นจะเสียความ
ยืดหยุ่นไปจนหมดสิ้น และไม่กลับคืนสู่รูปร่างเดิมอีกต่อไป
1. สมบัติของวัตถุที่เปลี่ยนรูปร่างเมื่อมีแรงมากระทำา และคืนรูปร่างเดิมได้เมื่อแรงนั้น
หมดไป
1. ความยืดหยุ่น ข. สภาพพลาสติก ค. ความเค้น ง.
ความเครียด
2. วัตถุที่มีความยืดหยุ่นสูงมีคุณสมบัติอย่างไร
ก. ไม่สามารถเปลี่ยนรูปร่างไปจากเดิมได้
ข. สามารถเปลี่ยนรูปร่างไปจากเดิมได้น้อยและไม่กลับคืนสู่สภาพเดิม
ค. สามารถเปลี่ยนรูปร่างจากเดิมได้มากและยังกลับคืนสู่สภาพเดิมได้
ง. สามารถเปลี่ยนรูปร่างไปจากเดิมได้มากและไม่กลับคืนสู่สภาพเดิมได้
3. ตำาแหน่งสุดท้ายของช่วงระยะที่ส่วนยืดของวัตถุแปรผันตรงกับขนาดของ
ก. ขีดจำากัดของการแปรผันตรง ข. ขีดจำากัดความยืดหยุ่น
ค. ขีดจำากัดความเค้น ง. ขีดจำากัดความเครียด
4. ตำาแหน่งสุดท้ายที่วัตถุยืดออกแล้วสามารถคืนตัวกลับสภาพเดิมได้
ก. ขีดจำากัดของการแปรผันตรง ข. ขีดจำากัดความยืดหยุ่น
ค. ขีดจำากัดความเค้น ง. ขีดจำากัดความเครียด
5. แรงภายในหรือแรงระหว่างโมเลกุลที่ยึดลวดไม่ให้ขาด มีขนาดเท่ากับนำ้าหนักของ
วัตถุที่แขวน
ก. แรงยืดหยุน ่ ข. แรงพลาสติก ค. แรงเค้น ง. แรงเครียด
6. อัตราส่วนระหว่างแรงเค้นกับพื้นที่หน้าตัดของเส้นลวด
ก. ความเครียด ข. ความยืดหยุ่น ค. ความเค้น ง.
ความเป็นพลาสติก
7. อัตราส่วนระหว่างขนาดรูปร่างที่เปลี่ยนไปต่อขนาดรูปร่างเดิม
- 13.
ก. ความเครียด ข. ความยืดหยุ่น ค. ความเค้น ง.
ความเป็นพลาสติก
8. ภายใต้ขีดจำากัดของความยืดหยุ่น ความเค้นกับความเครียดสัมพันธ์กันอย่างไร
ก. ความเค้นแปรผันตรงกับความเครียด ข. ความเค้นแปรผกผันกับ
ความเครียด
ค. เป็นไปตามกฎของ Hooke ง. ถูกทั้งข้อ ก. และ ข้อ ค.
9. วัตถุที่มีค่าความเค้นที่ขีดจำากัดความยืดหยุ่นตำ่าๆ หมายความว่า.....
ก. ทนแรงกระทำาจากภายนอกได้มาก และจะไม่กลับคืนสู่สภาพเดิม
ข. ทนแรงกระทำาจากภายนอกได้มาก และจะกลับคืนสู่สภาพเดิมได้
ค. ทนแรงกระทำาจากภายนอกได้เล็กน้อย และจะไม่กลับคืนสู่สภาพเดิม
ง. ทนแรงกระทำาจากภายนอกได้เล็กน้อย จึงจะกลับคืนสภาพเดิมได้
1. ลวดโลหะยาว 3 เมตร และมีพื้นที่หน้าตัด 0.25 ตารางเซนติเมตร จะยืดออก 0.05
เซนติเมตร เมื่อใช้แรงดึง 10000 นิวตัน จงหาความเค้นดึงและความเครียดดึง
2. ลวดโลหะยาว 10 เมตร มีพนที่หน้าตัด 0.05 ตารางเซนติเมตร เมื่อถ่วงด้วยนำ้าหนัก
ื้
10,000 นิวตัน จะยืดออกไป 10 เซนติเมตร โลหะนี้มีค่ามอดูลัสของยังเท่าไร
3. แขวนมวล 400 กิโลกรัมกับเส้นลวดโลหะชนิดหนึ่งยาว 10 เมตร มีพื้นที่หน้าตัด 2 x
10-4 ตารางเมตร ถ้าค่ามอดูลัสของยังของเส้นลวดเป็น 2 x 1011 นิวตัน/เมตร 2 ลวด
จะยืดออกเป็นระยะกี่เซนติเมตร
- 14.
4. เมื่อแขวนมวล Mไว้ที่ปลายเส้นลวด จะทำาให้เส้นลวดยืดออก 0.12% ของความยาว
เดิม ถ้าลวดมีพื้นที่หน้าตัด 0.2 ตารางมิลลิเมตร และมีค่ามอดูลัสของยังเท่ากับ เป็น
2.0 x 1011 นิวตัน / เมตร 2 มวล M มีค่าเท่าใด...