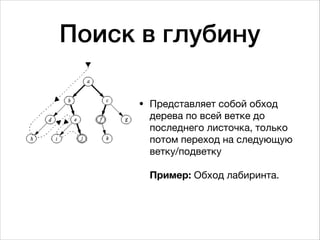
Документ обсуждает концепцию рекурсии, ее виды и примеры применения, такие как вычисление факториала и числа Фибоначчи. Он объясняет особенности, преимущества и недостатки рекурсии, а также затрагивает методы поиска в массиве, включая линейный и бинарный поиск, и описывает основы работы поисковых систем. Также представлены примеры кода для разных алгоритмов, связанных с рекурсией и поиском.








![Факториал через цикл
public class Factorial {
public static void main(String[] args) {
int result = factorialCycle(3);
System.out.println(result);
}
private static int factorialCycle(int n) {
int factorial = 1;
for (int i = 1; i <= n; i++) {
factorial *= i;
}
return factorial;
}
}](https://image.slidesharecdn.com/random-170830092348/85/slide-10-320.jpg)
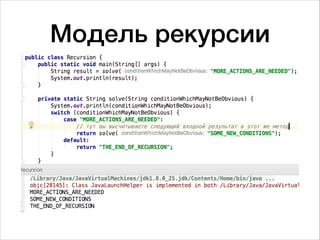
![Факториал через
рекурсию
public class Factorial {
public static void main(String[] args) {
int result = factorialRecursion(2);
System.out.println(result);
}
private static int factorialRecursion(int n) {
if (n > 1) {
return n * factorialRecursion(n - 1);
}
return 1;
}
}](https://image.slidesharecdn.com/random-170830092348/85/slide-11-320.jpg)

![Числа Фибоначчи
public class FibonachiNumbers {
public static void main(String[] args) {
int n = 6;
int result = fibonachi(n);
System.out.println(result);
}
private static int fibonachi(int n) {
//1, 1, 2, 3, 5, 8
if (n > 2){
return fibonachi(n - 1) + fibonachi(n - 2);
}
return 1;
}
}](https://image.slidesharecdn.com/random-170830092348/85/slide-13-320.jpg)





![Линейный поиск
public static void main(String[] args) {
int[] arr = {1, 15, 8, 2, 15, 19}; // где ищем
int x = 8; // что ищем
int i = linearSearch(arr, x);
System.out.println(i);
}
public static int linearSearch(int[] arr, int x){
for (int i = 0; i < arr.length; i++) {
int element = arr[i];
if (element == x){
return i;
}
}
return -1;
}](https://image.slidesharecdn.com/random-170830092348/85/slide-19-320.jpg)

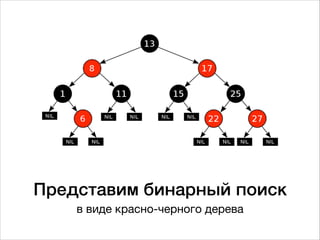
![Реализация бинарного
поиска
public class BinarySearch {
/**
* ищем индекс элемента в массиве
* или возвращаем -1, если элемента нету
*/
public static void main(String[] args) {
int[] arr = {1, 5, 8, 12, 15, 19}; // где ищем
int x = 15; // что ищем
int i = binarySearch(arr, x, 0, arr.length - 1);
System.out.println(i);
}
public static int binarySearch(int[] arr, int x, int low, int high) {
if (high < low) {
return -1; //не найдено
}
int mid = (low + high) / 2;
if (arr[mid] > x) {
//ищем в нижней части массива
return binarySearch(arr, x, low, mid - 1);
} else if (arr[mid] < x) {
//ищем в верхней части массива
return binarySearch(arr, x, mid + 1, high);
} else return mid; //найденный элемент
}
}](https://image.slidesharecdn.com/random-170830092348/85/slide-22-320.jpg)