This document discusses various algorithms and their time complexities: 1. Section A discusses sorting algorithms and their O(N) linear time complexity for small/large inputs. 2. Section B discusses interval intersection algorithms with O(M*N) quadratic time for small inputs using nested loops, and O(M*logM) logarithmic time for large inputs using disjoint set data structures. 3. Section C discusses image quilting algorithms with O(W*3H) cubic time for small images and O(W*H) linear time for large images using dynamic programming. 4. Section D discusses connected component labeling with linear time for small images using scanning and O(N*M) time for

1. 2017

2. A. 6
• Small/Large:
• N
• S
• C
• L
• .
• : O(N)

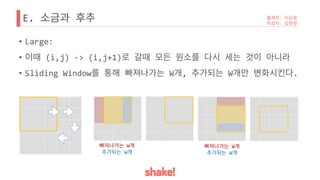
3. B.
• Small:
• check [x, y) 1 .
•
• [1, N] 1 .
• : O(M * N)

4. B.
• Large:
• x .
• r
• x y
• r y
• .

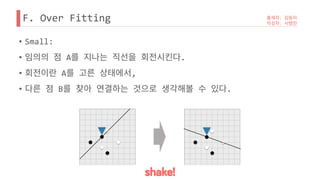
5. B.
•
• [1,6] ~ [3,9] r 6->8->9 ,
• [11,12] x r .
[1,6]
[2,5]
[3,8]
[3,9]
[11,12]
[12,16]

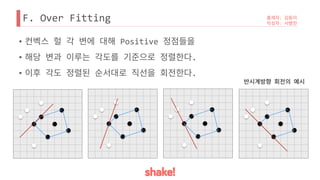
6. B.
• [11,12] ~ [12,16]
• [1,9], [11,16]
• .
[1,6]
[2,5]
[3,8]
[3,9]
[11,12]
[12,16]

7. B.
• : O(M * logM)
• x : O(M * logM)
• r : O(M)
• Disjoint-set .

8. C. Quilting
• Small:
•
• .
•
• : O(W * 3H)
• W
• : 3

9. C. Quilting
• Large:
• D[i][j]: (i,j) i
•
• D[i][j] D[i-1][j-1], D[i-1][j], D[i-1][j+1]
• .
D[i-1][j-1] D[i-1][j] D[i-1][j+1]
D[i][j]
?

10. C. Quilting
• D[i][j] = mindw = -1 to 1(D[i-1][j+dw]) + (A[i][j] – B[i][j])2
• : minj = 1 to W (D[N][j])
• ,
•
• : O(W * H)

11. D.
• 7 4 , 28 4x4 .
• .
• .
• if .
1 0 0 0
1 0 0 0
1 1 0 0
0 0 0 0
1 1 0 0
0 1 0 0
0 1 0 0
0 0 0 0
1 1 0 0
1 1 0 0
0 0 0 0
0 0 0 0
1 0 0 0
1 0 0 0
1 0 0 0
1 0 0 0

12. D.
• 0, 1 2 .
• 1
• 0
• 1
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 1 1 1 0 0 1 1 1 1 1 1
1 1 1 1 0 1 1 1 1 1 1 1
1 1 1 1 0 1 1 1 1 1 1 1
1 1 1 1 0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1

13. D.
• Small : .
1. .
1. .
2. .
2. .
1. 1 .
2. 1 .
3. .
3. .
1. .
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0
1 0 0 0
1 0 0 0
1 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0
1 0 0 0
1 0 0 0
1 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0
1 0 0 0
1 0 0 0
1 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0
1 0 0 0
1 0 0 0
1 0 0 0

14. D.
• Large : .
1. 1 .
1. .
2. BFS .
1. 1
1. 1 .
2. , .
3. .
2. 1 , ,
1. BFS .
2. .
3. .
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 1 1 1 0 0 1 1 1 1 1 1
1 1 1 1 0 1 1 1 1 1 1 1
1 1 1 1 0 1 1 1 1 1 1 1
1 1 1 1 0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0
1 0 0 0
1 0 0 0
1 0 0 0

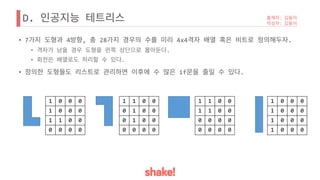
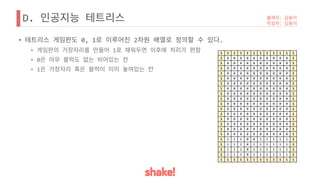
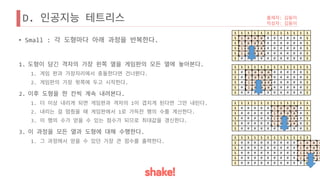
15. D.
• [Tip]
•
.
• .
• 4 .
•
• .
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 1
1 1 1 1 0 0 1 1 1 1 1 1
1 1 1 1 0 1 1 1 1 1 1 1
1 1 1 1 0 1 1 1 1 1 1 1
1 1 1 1 0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0
1 0 0 0
1 0 0 0
1 0 0 0

16. E.
• Small:
• (1,1) ~ (M,N)
• (i,j) W
• .
• .

17. E.
• Small:
• : O(N * M * W2 * logW)
• (1, 1) ~ (M, N): O(N * M)
• W X W : O(W2)
• : O(W2 * logW)
• : O(N * M) * (O(W2) + O(W2 * logW))

18. E.
• Large:
• X .
• (i,j) W X W
•
• : k
• Segment Tree, Fenwick Tree
• Binary Search (W2+1)/2 X .

19. E.
• Large:
• (i,j) -> (i,j+1)
• Sliding Window W , W .
W
W
W
W

20. E.
• : O(N * M * W * logK)
• (1, 1) ~ (M, N): O(N * M)
• : 2 * W
• 2 * W / , : O(W * logK)
• BinarySearch : logK
• BinarySearch : O(logK)
• : O(N * M) * (O(W * logK) + O((logK)2))

21. E.
• Large:
• Heap .
• 2W /
• MaxHeap MinHeap .
• MaxHeap
• MinHeap
• MinHeap MaxHeap 1
• MinHeap .

22. E.
• : O(N * M * W * logW)
• (1, 1) ~ (M, N): O(N * M)
• : 2 * W
• 2 * W / : O(W * logW)

23. F. Over Fitting
• Small:
• A .
• A ,
• B .

24. F. Over Fitting
• Small:
•
• N-2
• Positive ( / ) ,
• Positive .
• A, B Positive
.

25. F. Over Fitting
• Small:
• A, B
• Positive .
• : O(N3)
• : O(N2)
• : O(N)

26. F. Over Fitting
• A, B .
• Positive-Positive: Positive .
• Positive-Negative: .
• Negative-Negative: negative .
• Positive-Positive, Negative-Negative
• Positive-Negative
• Positive-Negative .

27. F. Over Fitting
• Negative
• Negative .
• Positive
• Negative-Positive
• .
• => Negative .

28. F. Over Fitting
• Positive
• .
• .

29. F. Over Fitting
• / ,
• / Positive
• Positive .
• Two Pointer O(N) Positive
.
• : O(N2 * logN)
• N
• : O(N * logN)
• / : O(N)