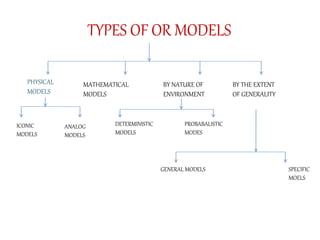
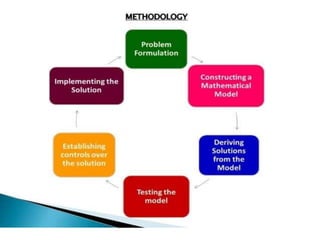
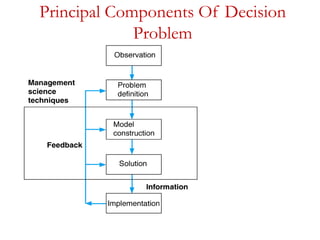
Resource management techniques involve efficiently using an organization's limited resources such as employees, equipment, and finances. Some key techniques include: 1. Linear programming, which uses mathematical models to determine the optimal allocation of resources to meet objectives and constraints. An example is determining the optimal product mix. 2. Operations research, which applies scientific principles and quantitative analysis to help maximize efficiency. It has been widely used by militaries and businesses since World War II. 3. Modeling real-world problems mathematically and using algorithms to determine the best solutions while optimizing objectives under constraints. This allows organizations to best utilize their resources.

1. Resource Management Techniques
Dr.G.GEETHA
Professor and Head
Department of CSE
Jerusalem College of Engineering

2. Class -1
• Resource Management techniques
• Operation Research
• History of OR
• Models
• Phases of Problem Solving/Decision Making

3. Resource
• These resources can include tangible resources
such as goods and equipment, financial
resources, and labor resources such as
employees
1. Man
2. Money
3. Material
4. Machine

4. Management
• Management means ―the process of dealing
with or controlling things or people
5. Method/ Management
6. Market

5. Techniques
• a skilful or efficient way of doing or achieving
something.

6. Resource Management
• Resource management is the process of
maximizing the efficient use of resources within
an organization.

7. Resource Management Techniques
Part of Operation Research

8. Introduction

9. Operations Research
 an Art and Science
• Operations
The activities carried out in an organization.
Research
The process of observation and testing characterized
by the scientific method. Situation, problem statement,
model construction, validation, experimentation, candidate
solutions.
• Operations Research is quantitative approach to decision
making based on the scientific method of problem solving.

10. 10
Terminology
• The British/Europeans refer to “Operational Research",
the Americans to “Operations Research" - but both are
often shortened to just "OR".
• Another term used for this field is “Management
Science" ("MS"). In U.S. OR and MS are combined
together to form "OR/MS" or "ORMS".
• Yet other terms sometimes used are “Industrial
Engineering" ("IE") and “Decision Science" ("DS").

11. 11
What is Operations Research?
• Operations Research is the scientific
approach to execute decision making, which
consists of:
– The art of mathematical modeling of
complex situations
– The science of the development of solution
techniques used to solve these models
– The ability to effectively communicate the
results to the decision maker

12. Smart Shoveling
• Taylor experimented with the
shape, size, and weight of shovels
to determine the impact on
productivity.
• His experiments showed that no
one shovel was best for all
materials. By designing task-
specific shovels, Taylor tripled the
amount of material a worker could
shovel in a day.
• This dramatically improved morale
as well since workers were paid by
the ton. Increasing productivity
meant increasing income.

13. History of Operation Research
• Operation research origins in World War II for military
services Urgent need to allocate resources at efficient
manner.
• British and US called large number of scientists from
discipline were asked to do research on military
operation.
Developed effective method to locate radar (Britain Air
Battle).
Developed a better method to manage convoy and
antisubmarine operation(North Atlantic).
Developed a method to utilize resources efficiently(
resource cost reduced one half).

14. 14
1890
Frederick Taylor
Scientific
Management
[Industrial
Engineering]
1900
•Henry Gannt
[Project Scheduling]
•Andrey A. Markov
[Markov Processes]
•Assignment
[Networks]
1910
•F. W. Harris
[Inventory Theory]
•E. K. Erlang
[Queuing Theory]
1920
•William Shewart
[Control Charts]
•H.Dodge – H.Roming
[Quality Theory]
1930
Jon Von Neuman –
Oscar Morgenstern
[Game Theory]
1940
•World War 2
•George Dantzig
[Linear
Programming]
•First Computer
1950
•H.Kuhn - A.Tucker
[Non-Linear Prog.]
•Ralph Gomory
[Integer Prog.]
•PERT/CPM
•Richard Bellman
[Dynamic Prog.]
ORSA and TIMS
1960
•John D.C. Litle
[Queuing Theory]
•Simscript - GPSS
[Simulation]
1970
•Microcomputer
1980
•H. Karmarkar
[Linear Prog.]
•Personal computer
•OR/MS Softwares
1990
•Spreadsheet
Packages
•INFORMS
2000……
History of oR

15. DISCIPLINE METHODS AND THEORIES
Physical Sciences
Mathematics
Political Sciences
Social Sciences
Business Administration
Behavior Science
Economics
Computer Science
. . .
Decision Theory
Mathematical Programming
Queuing Theories
Scheduling Theory
Reliability Theory
Probability& Statistics
Stochastic Process
Simulation
Inventory Theory
Network Theory
. . .
↘ ↙
Operations Research
↓
The Applications
↓
Education, Manufacturing, Heath, Finance, Energy and Utilities, Transportation,
Environmental, Military, Forest Management . . .

16. TYPES OF OR MODELS
SPECIFIC
MOELS
PHYSICAL
MODELS
MATHEMATICAL
MODELS
BY NATURE OF
ENVIRONMENT
BY THE EXTENT
OF GENERALITY
ICONIC
MODELS
ANALOG
MODELS
DETERMINISTIC
MODELS
PROBABALISTIC
MODES
GENERAL MODELS

17. 17
Operations Research Models
Deterministic Models Stochastic Models
• Linear Programming • Discrete-Time Markov Chains
• Network Optimization • Continuous-Time Markov Chains
• Integer Programming • Queuing Theory (waiting lines)
• Nonlinear Programming • Decision Analysis
• Inventory Models Game Theory
Inventory models
Simulation

18. 18
Deterministic vs. Stochastic Models
Deterministic models
Assume all data are known with certainty
Deterministic models involve optimization
Example: product mix
Stochastic models
Explicitly represent uncertain data via
random variables or stochastic processes.
Stochastic models
characterize / estimate system performance
stochastic modelling as applied to the insurance industry,
telecommunication , traffic control etc.

19. OR
• "OR is the representation of real-world systems
by mathematical models together with the use
of quantitative methods (algorithms) for solving
such models, with a view to optimizing."

20. Resource Management Techniques
• The process of using a company's resources in the most
efficient way possible.
• These resources can include tangible resources such as goods
and equipment, financial resources, and labor resources such
as employees.
• Resource management can include ideas such as making sure
one has enough physical resources for one's business, but not
an overabundance so that products won't get used, or making
sure that people are assigned to tasks that will keep them busy
and not have too much downtime.

21. Principal Components Of Decision
Problem

22. General approach to solve a problem
in operations research.
• Step 1 – Definition and Identification
of problem
• Step 3 – Deriving a solution – ...
• Step 4- Testing the model and the solution – ...
• Step 5- Implementation and control.

24. Principal Components Of Decision
Problem

25. Class- II
• Linear Programming Problem
• Formulating LPP
• Examples of LP Problems

26. Linear Programming Problem

27. Linear Programming Problem
• Mathematical programming is used to find the
best or optimal solution to a problem that
requires a decision or set of decisions about
how best to use a set of limited resources to
achieve a state goal of objectives.
• Linear programming requires that all the
mathematical functions in the model be linear
functions.

28. Linear Programming Problem
• Steps involved in mathematical
programming
– Conversion of stated problem into a mathematical
model that abstracts all the essential elements of the
problem.
– Exploration of different solutions of the problem.
– Finding out the most suitable or optimum solution.

29. 29
Mathematical Models
• Relate decision variables (controllable inputs) with fixed or
variable parameters (uncontrollable inputs).
• Frequently seek to maximize or minimize some objective
function subject to constraints.
• Are said to be stochastic if any of the uncontrollable
inputs (parameterss) is subject to variation (random),
otherwise are said to be deterministic.
• Generally, stochastic models are more difficult to analyze.
• The values of the decision variables that provide the
mathematically-best output are referred to as the optimal
solution for the model.

30. FORMULATING LPP
Mathematical model as consisting of:
• Decision variables, which are the unknowns to be
determined by the solution to the model.
• Constraints to represent the physical limitations
of the system
• An objective function
• An optimal solution to the model is the
identification of a set of variable values which are
feasible (satisfy all the constraints) and which lead
to the optimal value of the objective function.

31. The Linear Programming Model (1)
Let: X1, X2, X3, ………, Xn = decision variables
Z = Objective function or linear function
Requirement: Maximization of the linear function Z.
Z = c1X1 + c2X2 + c3X3 + ………+ cnXn …..Eq (1)
subject to the following constraints:
…..Eq (2)
where aij, bi, and cj are given constants.where aij, bi, and cj are given constants.
…..Eq (2)

32. The Linear Programming Model (2)
• The linear programming model can be written in
more efficient notation as:
…..Eq (3)
The decision variables, xI, x2, ..., xn, represent levels of n competing
activities.
…..Eq (3)

33. Examples of LP Problems
• Product Mix Problem
• Blending Problem
• Production Scheduling Problem
• Transportation Problem
• Flow Capacity Problem

34. Four basic assumptions in LP:
• Proportionality /Linearity
The contribution to the objective function from each
decision variable is proportional to the value of the
decision variable
• Additivity
The value of objective function is the sum of the
contributions from each decision variables
• Divisibility
Each decision variable is allowed to assume fractional
values
• Certainty / Non Negativity

35. Giapetto Example
• Giapetto's wooden soldiers and trains. Each soldier sells for $27,
uses $10 of raw materials and takes $14 of labor & overhead costs.
Each train sells for $21, uses $9 of raw materials, and takes $10 of
overhead costs. Each soldier needs 2 hours finishing and 1 hour
carpentry; each train needs 1 hour finishing and 1 hour carpentry.
Raw materials are unlimited, but only 100 hours of finishing and
80 hours of carpentry are available each week. Demand for trains
is unlimited; but at most 40 soldiers can be sold each week. How
many of each toy should be made each week to maximize profits?

36. Answer
• Decision variables completely describe the
decisions to be made (in this case, by
Giapetto). Giapetto must decide how many
soldiers and trains should be manufactured
each week. With this in mind, we define:
• x1 = the number of soldiers produced per week
• x2 = the number of trains produced per week

37. • Objective function is the function of the
decision variables that the decision maker wants
to maximize (revenue or profit) or minimize
(costs). Giapetto can concentrate on maximizing
the total weekly profit (z).
• Here profit equals to (weekly revenues) – (raw
material purchase cost) – (other variable costs).
Hence Giapetto’s objective function is:
• Maximize z = 3x1 + 2x2

38. • Constraints show the restrictions on the values of the
decision variables. Without constraints Giapetto could
make a large profit by choosing decision variables to be
very large. Here there are three constraints:
• Finishing time per week
• Carpentry time per week
• Weekly demand for soldiers
• Sign restrictions are added if the decision variables can
only assume nonnegative values (Giapetto can not
manufacture negative number of soldiers or trains!)

39. • All these characteristics explored above give the
following Linear Programming (LP) model
max z = 3x1 + 2x2 (The Objective function)
s.t. 2x1 + x2 <= 100 (Finishing constraint)
x1 + x2 <= 80 (Carpentry constraint)
x1 <= 40 (Constraint on demand for soldiers)
x1, x2 > 0 (Sign restrictions)