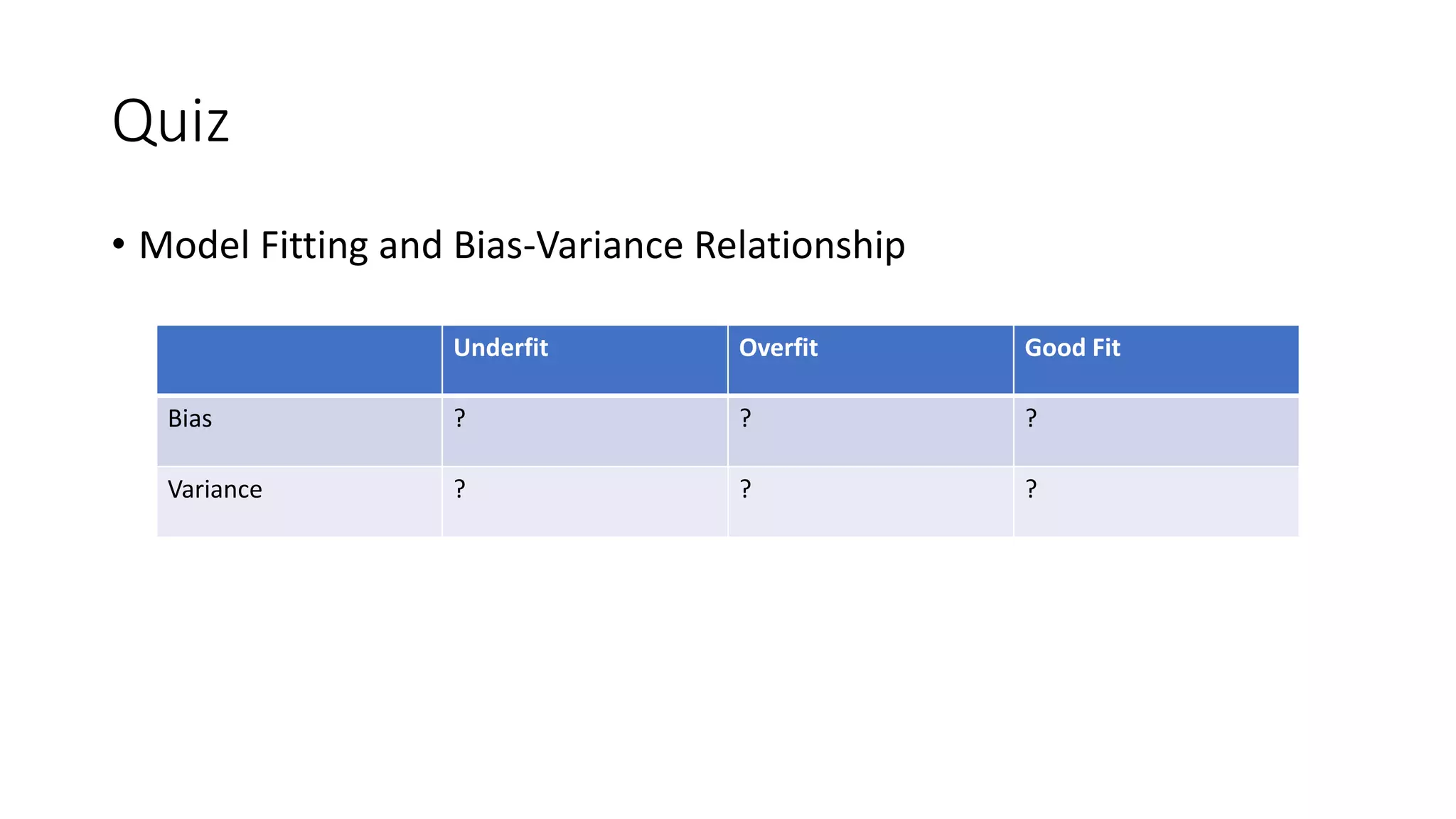
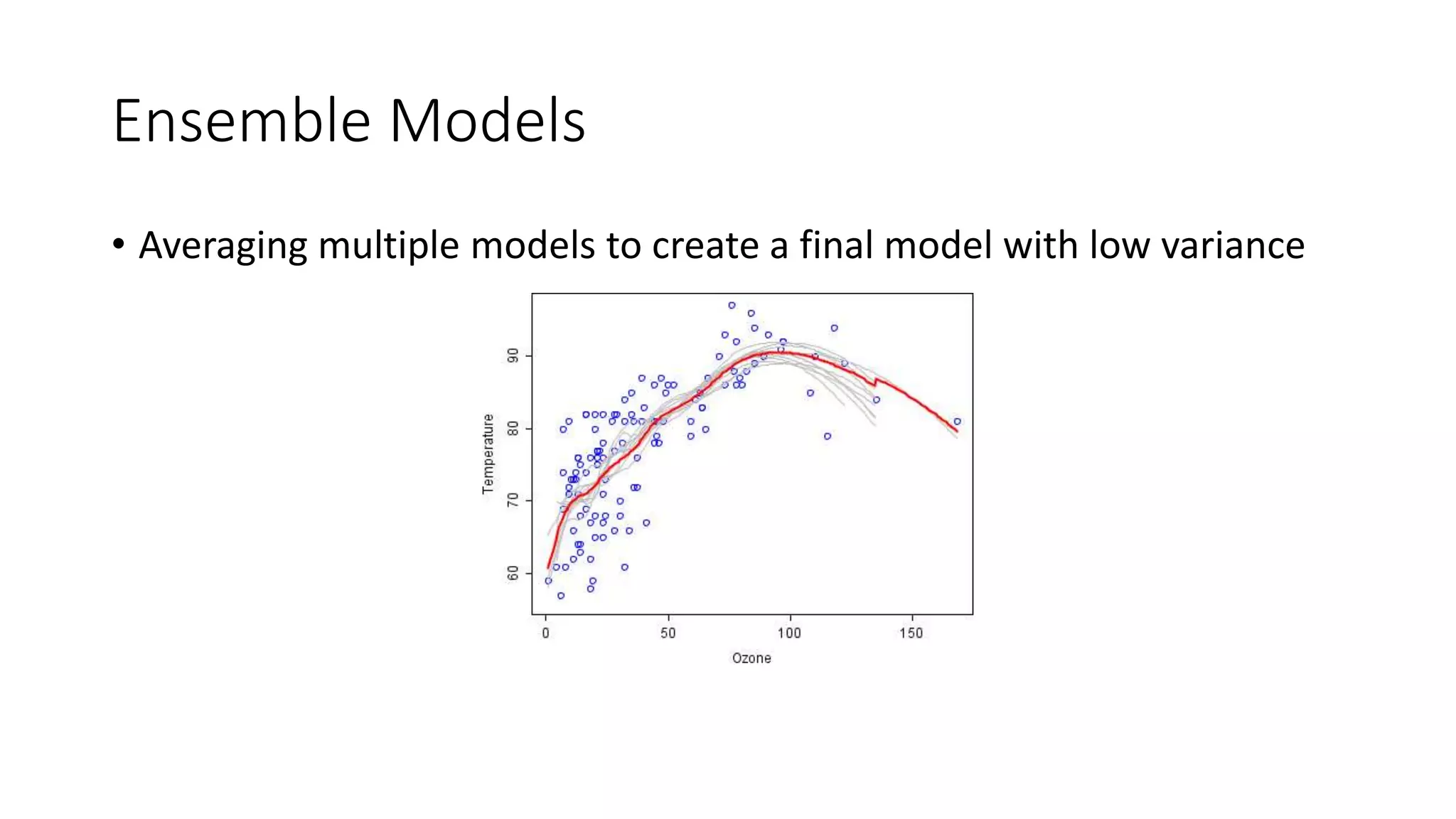
The document discusses model fitting in deep learning, focusing on the concepts of underfitting and overfitting, and the importance of regularization techniques to improve model generalization. It details various regularization approaches such as early stopping, L1/L2 regularization, batch normalization, and dropout, explaining their mechanisms and effectiveness. Key takeaways include the relationships between model complexity, bias, variance, and methods to reduce overfitting for better performance in machine learning models.

1. Vietnam Japan AI Community 2019-05-26
Kien Le
Regularization In
Deep Learning

3. Model Fitting Introduction

4. Model (Function) Fitting
• How well a model performs on training/evaluation datasets will
define its characteristics
Underfit Overfit Good Fit
Training Dataset Poor Very Good Good
Evaluation Dataset Very Poor Poor Good

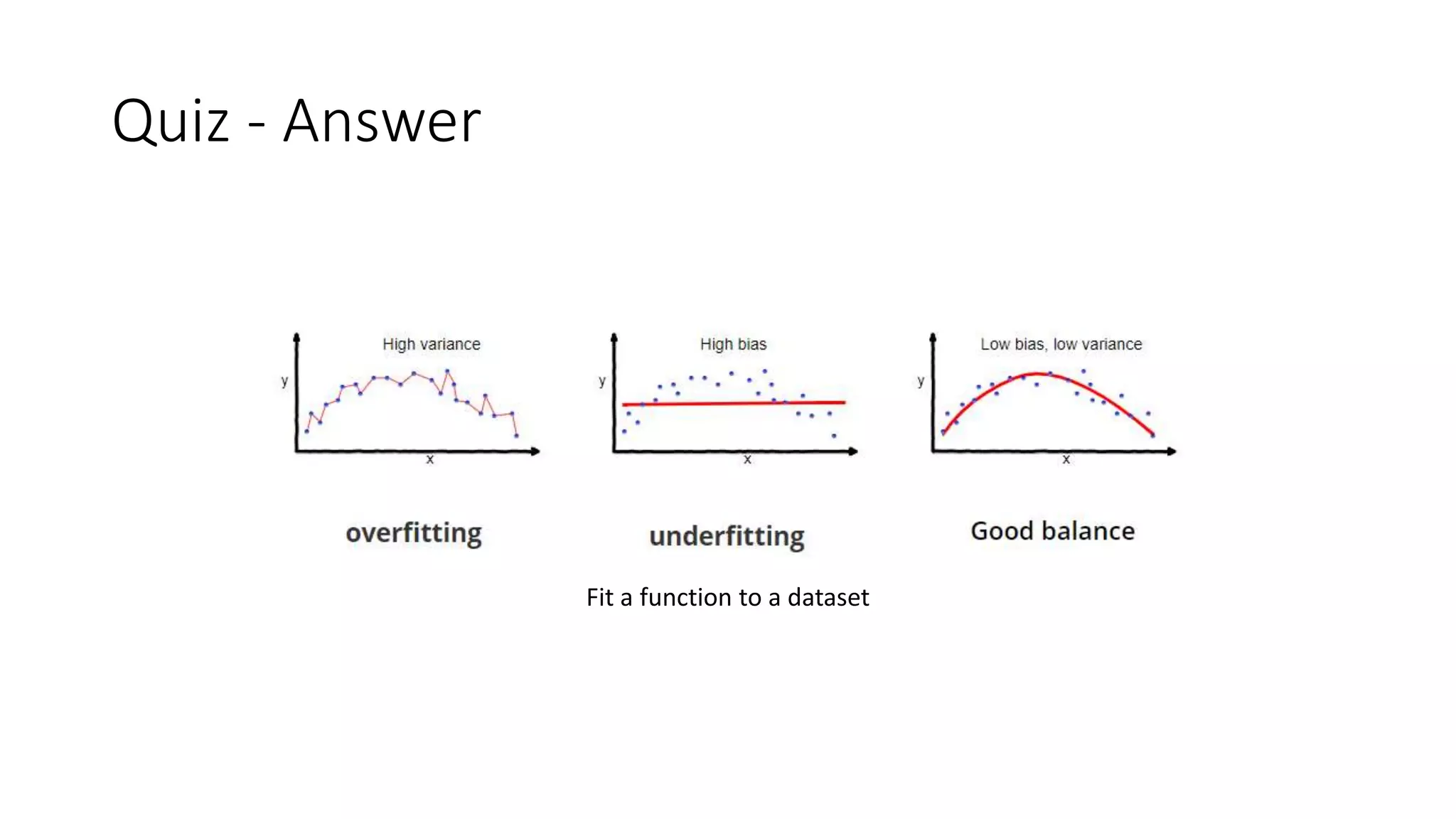
5. Model Fitting – Visualization
Variations of model fitting [1]

6. Bias Variance
• Prediction errors [2]
𝐸𝑟𝑟𝑜𝑟 𝑥 = (𝐸 𝑓 𝑥 − 𝑓 𝑥 )2+𝐸 𝑓 𝑥 − 𝐸[ 𝑓 𝑥 ]
2
(Bias)2 Variance
𝐸𝑟𝑟𝑜𝑟 = (𝐴𝑣𝑔 𝑃𝑟𝑒𝑑𝑖𝑐𝑡𝑒𝑑 − 𝑇𝑟𝑢𝑒)2+𝐴𝑣𝑔(𝑃𝑟𝑒𝑑𝑖𝑐𝑡𝑒𝑑 − 𝐴𝑣𝑔(𝑃𝑟𝑒𝑑𝑖𝑐𝑡𝑒𝑑))2

7. Bias Variance
• Bias
• Represents the extent to which average prediction over all data sets differs
from the desired regression function
• Variance
• Represent the extent to which the model is sensitive to the particular choice
of data set

8. Quiz
• Model Fitting and Bias-Variance Relationship
Underfit Overfit Good Fit
Bias ? ? ?
Variance ? ? ?

9. Quiz - Answer
Fit a function to a dataset

10. Regularization Introduction

11. Counter Underfit
• What causes underfit?
• Model capacity is too small to fit the training dataset as well as generalize to
new dataset.
• High bias, low variance
• Solution
• Increase the capacity of the model
• Examples:
• Increase number of layers, neurons in each layer, etc.
• Result:
• Lower Bias
• Underfit  Good Fit?

12. Counter Underfit
• It’s so simple, just turn it into an overfit model! 

13. Counter Overfit
• What cause overfit?
• Model capacity is so big that it adapts too well to training samples  Unable
to generalize well to new, unseen samples
• Low bias, high variance
• Solution
• Regularization
• But How?

14. Regularization Definition
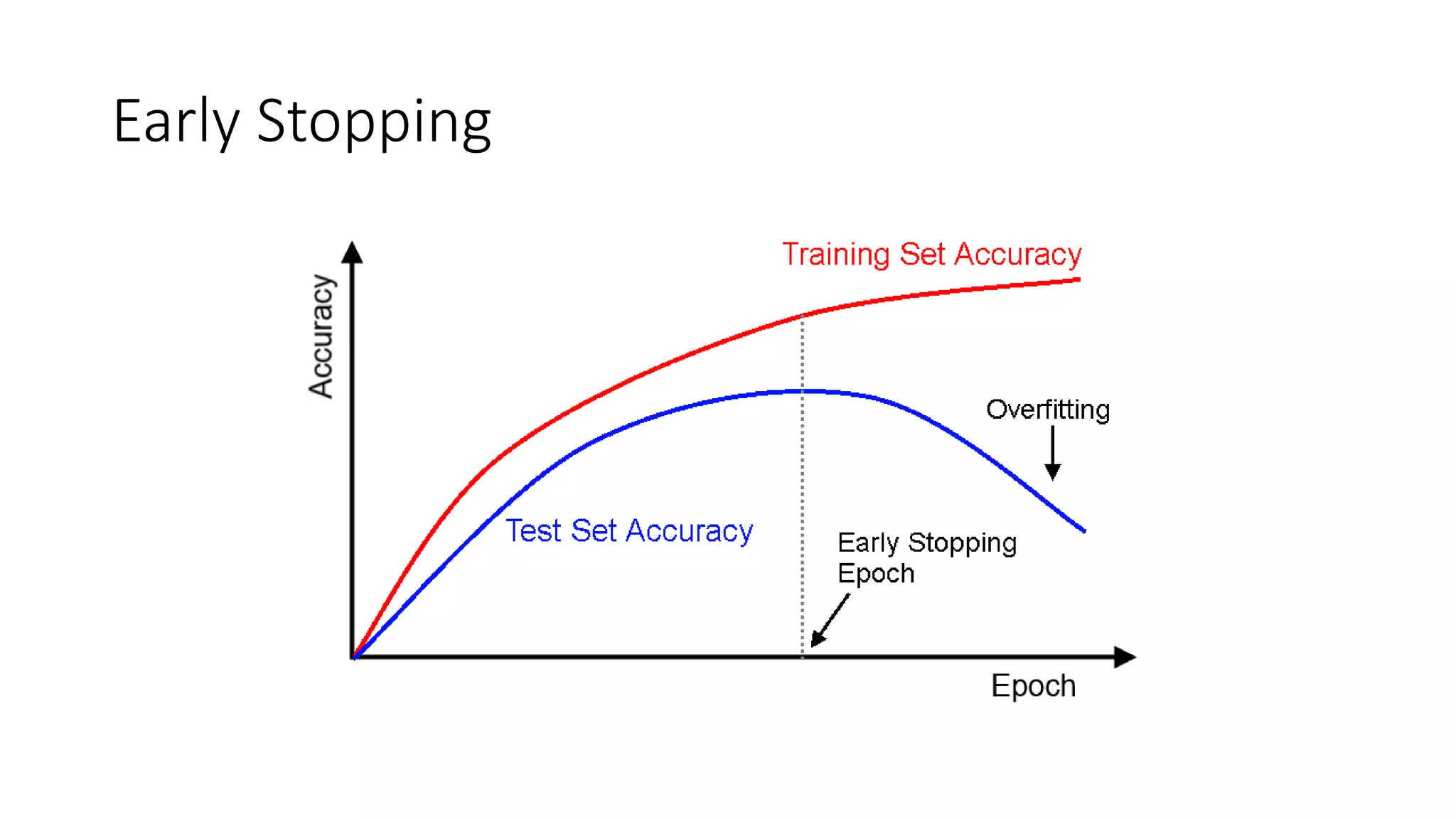
• Regularization is any modification we make to a learning algorithm
that is intended to reduce its generalization error but not its training
error. [4]

15. Regularization
Techniques
Early Stopping, L1/L2,
Batch Norm, Dropout

16. Regularization Techniques
• Early Stopping
• L1/L2
• Batch Norm
• Dropout
• Data Augmentation
• Layer Norm
• Weight Norm

17. Early Stopping
• There is point during training a large neural net when the model will
stop generalizing and only focus on learning the statistical noise in the
training dataset.
• Solution
• Stop whenever generalization errors increases

18. Early Stopping

19. Early Stopping
• Pros
• Very simple
• Highly recommend to use for all training along with other techniques
• Keras Implementation has option to save BEST_WEIGHT
• https://keras.io/callbacks/
• Callback during training
• Cons
• May not work so well

20. L1/L2 Regularization
• L2 adds “squared magnitude” of coefficient as penalty term to the
loss function.
𝐿𝑜𝑠𝑠 = 𝐿𝑜𝑠𝑠 + 𝜆 𝛽2
• L1 adds “absolute value of magnitude” of coefficient as penalty term
to the loss function.
𝐿𝑜𝑠𝑠 = 𝐿𝑜𝑠𝑠 + 𝜆 |𝛽|
• Weight Penalties  Smaller Weights  Simpler Model  Less Overfit

21. L1/L2 Regularization
• Regularization works on assumption that smaller weights generate
simpler model and thus helps avoid overfitting. [5]
• Why?

22. L1/L2 Comparison
• Robustness
• Sparsity

23. Robustness (Against Outliers)
• L1>L2
• The loss of outliers increase
• Exponentially in L2
• Linearly in L1
• L2 pays more efforts to deal with outliers  Less Robust

24. Sparsity
• L1>L2
• L1 zeros out coefficients, which leads to a sparse model
• L1 can be used for feature (coefficients) selection
• Unimportant ones have zero coefficients
• L2 will produce small values for almost all coefficients
• E.g: When applying L1/L2 to a layer with 4 weights, the results might
look like
• L1: 0.8, 0, 1, 0
• L2: 0.3,0.1,0.3, 0.2

25. Sparsity ([3])
𝑤1 = 𝑤1 − 0.5 ∗ 𝑔𝑟𝑎𝑑𝑖𝑒𝑛𝑡 𝑤1 = 𝑤1 − 0.5 ∗ 𝑔𝑟𝑎𝑑𝑖𝑒𝑛𝑡
gradient is constant (1 or -1)
w1: 5->0 in 10 steps
gradient is smaller over time (
w2: 5->0 in a big number of steps

26. L1/L2 Regularization
• Fun Fact:
• What does “L” in L1/L2 stand for?

27. Batch Norm
• Original Paper Title:
• Batch Normalization: Accelerating Deep Network Training by Reducing
Internal Covariate Shift [6]
• Internal Covariate Shift:
• The change in the distribution of network activations due to the change in
network parameters during training.

28. Internal Covariate Shift (More)
• Distribution of each layer’s inputs changes during training as the
parameters of the previous layers change.
• The layers need to continuously adapt to the new distribution!
• Problems:
• Slower training
• Hard to use big learning rate

29. Batch Norm Algorithm
• Batch Norm tries to fix the means and variances of layer inputs
• Reduce Internal Covariate Shift
• Run over batch axis

30. Batch Norm Regularization Effect
• Each hidden units are multiplied by a random value at each step of
training
 Add noises to training process
 Force layers to learn harder to be robust a lot of variation of inputs
 A form of data augmentation

31. Batch Norm Recap
• Pros
• Networks train faster
• Allow higher learning rates
• Make weights easier to initialize
• Make more activation functions viable
• Regularization by forcing layers to be more robust to noises (may replace Dropout)
• Cons
• Not good for online learning
• Not good for RNN, LSTM
• Different calculation between train and test
• Related techniques
• Layer norm
• Weight norm

32. Dropout
• How it works
• Randomly selected neurons are ignored during each training step.
• Dropped neurons don’t have effect on next layers.
• Dropped neurons are not updated in backward training.
• Questions:
• What’re the ideas?
• Why dropout help to reduce overfit?

33. Ensemble Models - Bagging
• How it works
• Train multiple models on different subsets of data
• Combine those models into a final model
• Characteristics
• Each sub-model is trained separately
• Each sub-model is normally overfit
• The combination of those overfit models produce a less overfit model overall

34. Ensemble Models
• Averaging multiple models to create a final model with low variance

35. Dropout - Ensemble Models for DNN
• Can we apply Bagging for Neural Network?
• It’s computationally prohibitive
• Dropout aims to solve this problem by providing a method to
combine multiple models with practical computation cost.

36. Dropout
• Removing units from base model effectively creates a subnetwork.
• All those subnetworks are trained implicitly together with all
parameters shared (different from bagging)
• At predict mode, all learned units are activated, which averages all
trained subnetworks

37. Dropout – Regularization Effect
• Each hidden units are multiplied by a random value at each step of
training
 Add noises to training process
 Similar with Batch Norm

38. Regularization Summary
• Two types of regularization
• Model optimization: Reduce the model complexity
• Data augmentation: Increase the size of training data
• Categorize techniques we have learned
• Model optimization: ?
• Data augmentation: ?

39. Demo Batch Norm, Dropout

40. Notes
• MNIST Dataset
• To create overfit scenario
• Reduce dataset size (60K->1K)
• Create a complex (but not so good) model
• Techniques to try
• Early stopping
• Dropout
• Batch Norm
• Link:
• https://drive.google.com/drive/u/0/folders/14A6n8bdrJHmgUcaopv66g8p0y
0ot6hSr

41. Key Takeaways
• Keywords: Overfit, Underfit, Bias, Variance
• Regularization Techniques: Dropout, Batch-Norm, Early Stopping

42. References
• [1] https://medium.com/greyatom/what-is-underfitting-and-overfitting-in-machine-
learning-and-how-to-deal-with-it-6803a989c76
• [2] Pattern Recognition and Machine Learning, M. Bishop
• [3] https://stats.stackexchange.com/questions/45643/why-l1-norm-for-sparse-models
• [4] Deep Learning, Goodfellow et. al
• [5] https://medium.com/datadriveninvestor/l1-l2-regularization-7f1b4fe948f2
• [6] Batch Normalization: Accelerating Deep Network Training by Reducing Internal
Covariate Shift, Sergey Ioffe et al
• [7] https://towardsdatascience.com/batch-normalization-8a2e585775c9
• [8] Dropout: A Simple Way to Prevent Neural Networks from Overfitting Srivastava et al
• [9] https://machinelearningmastery.com/train-neural-networks-with-noise-to-reduce-
overfitting/
• [10] Popular Ensemble Methods: An Empirical Study, Optiz et. al